Lerninhalte in Mathe

Abi-Aufgaben GK (GTR)

Abi-Aufgaben GK (CAS)

Digitales Schulbuch

Inhaltsverzeichnis

Aufgabe 2

Aufgabenstellung

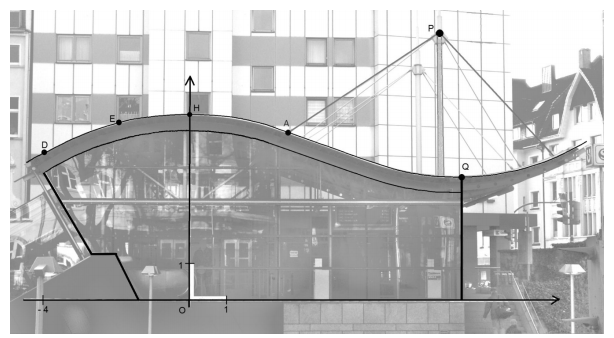
Grafik einer geschwungenen Struktur mit Bezug zu städtischen Gebäuden und einem Diagramm.

Abb. 1

Die Abbildung zeigt das Eingangsgebäude zu einer U-Bahn-Haltestelle. Auf dem Foto schaut man frontal auf eine ebene Glasfläche, die sich unter dem geschwungenen Dach befindet.
Eine Längeneinheit in dem eingezeichneten Koordinatensystem entspricht $1$ $\text{m}$ .
Der höchste Punkt der Dachoberkante befindet sich in diesem Koordinatensystem bei $H (0 \mid5,0)$ und der tiefste Punkt bei $Q (7,3 \mid 3,3)$ . Auch die Punkte $D ( -4 \mid 4)$ und $E ( -2 \mid 4,75)$ liegen auf der Dachoberkante.

a)

Die Profillinie der Dachoberkante hat eine geschwungene Form, die durch eine ganzrationale Funktion modelliert werden soll.

(1)

Die Profillinie hat im Bereich $-4 \leq x \leq 4$ näherungsweise die Form einer Parabel $2.$ Grades.
Bestimme eine Gleichung dieser Parabel mit dem Hochpunkt $H$ , die durch den Punkt $D$ verläuft.
Prüfe, ob der Punkt $E$ auf dieser Parabel liegt.
[Zur Kontrolle: $p(x)=- \dfrac{1}{16} \cdot x^2 +5$ ]

(5P)

(2)

Begründe anhand der Abbildung, warum eine ganzrationale Funktion, die zur Modellierung der gesamten Profillinie der Dachoberkante geeignet sein könnte, mindestens $3.$ Grades sein muss.

(3P)

Im Folgenden wird zur Modellierung der Dachoberkante für $- 4,5 \leq x \leq 10,5$ eine ganzrationale Funktion $4.$ Grades verwendet, und zwar die auf $\mathbb{R}$ definierte Funktion $f$ mit

$f(x) = 0,0004 \cdot x^4 + ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

b)

(1)

Weise nach, dass der Punkt $H$ auch ein lokaler Hochpunkt des Graphen von $f$ ist.

(4P)

(2)

Bestimme im Modellierungsbereich den Tiefpunkt $T$ des Graphen von $f$ .
Gib an, um wieviel Prozent jede Koordinate von $T$ von der entsprechenden Koordinate von $Q$ abweicht.
[Kontrollergebnis: $T (7,5 \mid 3,4)$ , $y$ -Wert gerundet]

(8P)

(3)

Der Punkt $A$ aus der Abbildung hat die $x$ -Koordinate $2,7$ .
Untersuche im Modell der Funktion $f$ , ob an dieser Stelle die Profillinie zwischen $H$ und $T$ das stärkste Gefälle hat.

(5P)

c)

Oberhalb des Daches sind geradlinig verlaufende Stahlseile angebracht. Gehe vereinfachend davon aus, dass das Stahlseil von $A (2,7 \mid f (2,7))$ nach $P (6,7 \mid 7,2)$ verläuft.

(1)

Berechne die Länge des Stahlseils von $A$ nach $P$ .

(4P)

(2)

Das Stahlseil wird im Bereich $2,7 \leq x \leq 6,7$ durch eine Gerade $g$ modelliert.
Bestimme eine Gleichung der Geraden $g$ und berechne die Größe des Winkels, den die Gerade $g$ in $A$ mit der Horizontalen einschließt.

(6P)

(3)

Ein weiteres Seil soll von $P$ nach $E$ gespannt werden.
Überprüfe, ob es in $E$ tangential zur Dachoberkante verlaufen wird.

(4P)

d)

Das Eingangsgebäude ist mit Glas verkleidet. Gehe vereinfachend davon aus, dass es sich bei der in der Abbildung umrahmten Glasfläche um eine durchgehende ebene Fläche handelt, die nicht durch Rahmen und Streben unterbrochen wird.
Die eingezeichnete Oberkante der Glasfläche wird im Bereich $-4 \leq x \leq 7,3$ durch die auf $\mathbb{R}$ definierte Funktion

$h$ mit $h(x)= 0,0004 \cdot x^4 + ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

modelliert.

(1)

Berechne den Inhalt der Glasfläche von der $y$ -Achse bis zur eingezeichneten Kante durch den Punkt $Q$ in der Ansicht aus der Abbildung.

(6P)

(2)

Für die Glasfläche links von der $y$ -Achse ist der Rand der zu berechnenden Glasfläche in der Abbildung nachgezeichnet.
Beschreibe eine mögliche Lösungsidee zur Bestimmung des Inhalts der umrahmten Glasfläche links von der $y$ -Achse. Gib dabei alle nötigen Ansätze an, die Berechnung konkreter Werte wird hingegen nicht erwartet.

(5P)

Bildnachweise [nach oben]

[1]

© 2016 - Ministerium für Schule und Weiterbildung des Landes Nordrhein-Westfalen.

a)

1)

$\blacktriangleright$ Parabelgleichung bestimmen

Du sollst eine Gleichung der Parabel zweiten Grades bestimmen, die durch den Punkt $D(-4\mid 4)$ verläuft und deren Hochpunkt bei $H(0\mid 5)$ liegt. Die allgemeine Funktionsgleichung einer Parabel $p$ zweiten Grades lautet wie folgt:

$p(x) = ax^2 +bx +c$

Mit Hilfe der beiden angegebenen Punkte $D$ und $H$ kannst du ein lineares Gleichungssystem aufstellen, das du nach den Parametern $a$ , $b$ und $c$ lösen kannst. Beachte dabei auch das notwendige Kriterium für einen Hochpunkt an der Stelle $x_E$ :

$p‘(x_E)=0$

Um das Gleichungssystem aufzustellen, benötgist du die erste Ableitung $p‘$ der gesuchten Funktion:

$p‘(x)= 2ax +b$

Nun erhältst du folgende Bedingungen:

$p‘(0)=0$
$p(0)=5$
$p(-4)=4$

Du erhältst folgendes Gleichungssystem:

$\begin{array}{} \text{I}\quad&0&=&2a\cdot 0 +b \\ \text{II}\quad&5&=& a\cdot 0^2 + b\cdot 0 + c\\ \text{III}\quad&4&=& a (-4)^2 + b(-4) +c\\ \end{array}$

Aus $\text{I}$ erhältst du direkt $b = 0$ und aus $\text{II}$ folgt $c = 5$ . Setze diese Ergebnisse noch in $\text{III}$ ein, um $a$ zu berechnen:

$a = \dfrac{-1}{16}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Eine Gleichung der gesuchten Parabel lautet $p(x) = -\dfrac{1}{16}x^2 +5$ .

$\blacktriangleright$ Punktprobe

Um zu überprüfen, ob der Punkt $E(-2\mid 4,75)$ auf der Parabel liegt, setze die Koordinaten in die oben bestimmte Funktionsgleichung ein:

$\begin{array}[t]{rll} p(x)&=& -\dfrac{1}{16}x^2 +5\\[5pt] 4,75&=& -\dfrac{1}{16}\cdot (-2)^2 +5 \\[5pt] 4,75&=&4,75 \\[5pt] \end{array}$

Also liegt der Punkt $E$ auf der Parabel.

(2)

$\blacktriangleright$ Grad der Funktion begründen

Du sollst begründen, dass eine geeignete Funktion zur Modellierung der gesamten Dachoberkante mindestens den Grad drei haben muss. Untersuche den Graphen dafür auf markante Punkte wie Hoch- oder Tiefpunkte und überlege dir, wie viele solcher Punkte eine Funktion mit geringerem Grad höchstens haben kann.

Der Abbildung kannst du entnehmen, dass die Linie der Dachkante einen lokalen Hochpunkt, aber auch einen lokalen Tiefpunkt besitzt. Der Graph einer Funktion zweiten Grades kann aber nur einen lokalen Extrempunkt besitzen und der einer linearen Funktion (Grad eins) besitzt keinen solchen Punkt. Daher muss die Funktion mindestens den Grad drei haben.

b)

(1)

$\blacktriangleright$ Hochpunkt nachweisen

Deine Aufgabe ist es, nachzuweisen, dass der Punkt $H(0\mid 5)$ auch ein Hochpunkt des Graphen von $f$ ist. Beachte dabei die beiden Kriterien für einen Hochpunkt an der Stelle $x_H$ :

Notwendiges Kriterium: $f‘(x_H)=0$
Hinreichendes Kriterium: $f‘‘(x_H)< 0$

Du kannst also wie folgt vorgehen:

Bestimme die ersten beiden Ableitungsfunktionen von $f$ .
Überprüfe das notwendige Kriterium, indem du $f‘(0)$ berechnest.
Überprüfe das hinreichende Kriterium durch Einsetzen in die zweite Ableitungsfunktion.
Überprüfe die $y$ -Koordinate durch Einsetzen in $f(x)$ .

1. Schritt: Ableitungen bilden

Bilde die Ableitungen mit den dir bekannten Ableitungsregeln:

\( \)

\begin{array}[t]{rll} f(x)&=&... \\[10pt] f‘(x)&=&... \\[10pt] f‘‘(x)&=&... \\[5pt] \end{array} \( \)

\( \)

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

2. Schritt: Notwendiges Kriterium überprüfen

Setze $x_H =0$ in $f‘(x)$ ein:

$f‘(x_H)=f‘(0)=0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

3. Schritt: Hinreichendes Kriterium überprüfen

Einsetzen in $f‘‘(x)$ liefert:

$f‘‘(x_H)= f‘‘(0)=0,126 \neq 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

4. Schritt: Koordinaten überprüfen

Einsetzen in $f(x)$ liefert:

$f(x_H)=f(0)=5$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Also ist $H(0\mid 5)$ ebenfalls ein Hochpunkt des Graphen von $f$ .

(2)

$\blacktriangleright$ Tiefpunkt bestimmen

Die Koordinaten des Tiefpunkts kannst du entweder mit Hilfe deines GTRs oder handschriftlich über die Kriterien für einen Tiefpunkt an der Stelle $x_T$ bestimmen:

Notwendiges Kriterium: $f‘(x_T)=0$
Hinreichendes Kriterium: $f‘‘(x_T)> 0$

Beachte, dass du auch die Intervallgrenzen auf mögliche Randextrema überprüfen musst.

$\blacktriangleright$ Lösungsweg A: Handschriftlich

Du kannst wie folgt vorgehen:

Wende das notwendige Kriterium an, indem du $f‘(x)=0$ setzt und so mögliche Extremstellen bestimmst.
Überprüfe das hinreichende Kriterium durch Einsetzen in die zweite Ableitungsfunktion.
Berechne die $y$ -Koordinate des Tiefpunkts durch Einsetzen in $f(x)$ .
Berechne die Funktionswerte an den Intervallgrenzen um mögliche Randextrema auszuschließen.

1. Schritt: Notwendiges Kriterium anwenden

$x_1 = 0$ und $x^2 +3x-78,75= 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Du kannst nun die p-q-Formel anwenden, um weitere Lösungen der Gleichung zu bestimmen:

$\begin{array}[t]{rll} x_2&=&-\dfrac{3}{2} + 9 \\[5pt] &=& 7,5 \\[10pt] x_3&=& -\dfrac{3}{2} - 9 \\[5pt] &=& -10,5 \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Für die Modellierung ist nur der Bereich $-4,5 \leq x \leq 10,5$ relevant, also fällt $x_3$ aus der Betrachtung raus. Bei $x_1$ handelt es sich laut Abbildung um eine Maximalstelle.

2. Schritt: Hinreichendes Kriterium überprüfen

Einsetzen von $x_2=7,5$ in $f‘‘(x)$ liefert:

$\begin{array}[t]{rll} f‘‘(x_2)&=&f‘‘(7,5) \\[5pt] &=& 0,216 > 0 \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

An der Stelle $x_2 = 7,5$ besitzt der Graph von $f$ einen lokalen Tiefpunkt.

3. Schritt: Funktionswert berechnen

Die $y$ -Koordinate des lokalen Tiefpunkts erhältst du durch Einsetzen von $x_2$ in $f(x)$ :

$y_T \approx 3,40$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

4. Schritt: Intervallgrenzen überprüfen

Überprüfe die Grenzen des Modellierungsbereichs $x_0 = -4,5$ und $x_4 = 10,5$ auf Randextrema.

$\begin{array}[t]{rll} f(-4,5)&\approx &3,74 \, > \, 3,4 \\[10pt] f(10,5)&\approx& 4,77 \, > \, 3,4\\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Funktiuonswerte an den Intervallgrenzen sind größer als der Funktionswert des lokalen Tiefpunkts. Damit ist der lokale Tiefpunkt mit den gerundeten Koordinaten $T(7,5\mid 4,4)$ auch der Tiefpunkt des gesamten Modellierungsbereichs.

$\blacktriangleright$ Lösungsweg B: GTR

Mit deinem GTR kannst du einen lokalen Tiefpunkt bestimmen, indem du dir den Graphen von $f$ anzeigen lässt. Den Befehl für einen Tiefpunkt findest du dann unter:

2ND $\to$ TRACE (CALC) $\to$ 3: minimum

Du erhältst folgendes gerundetes Ergebnis:

$T(7,5\mid 4,4)$

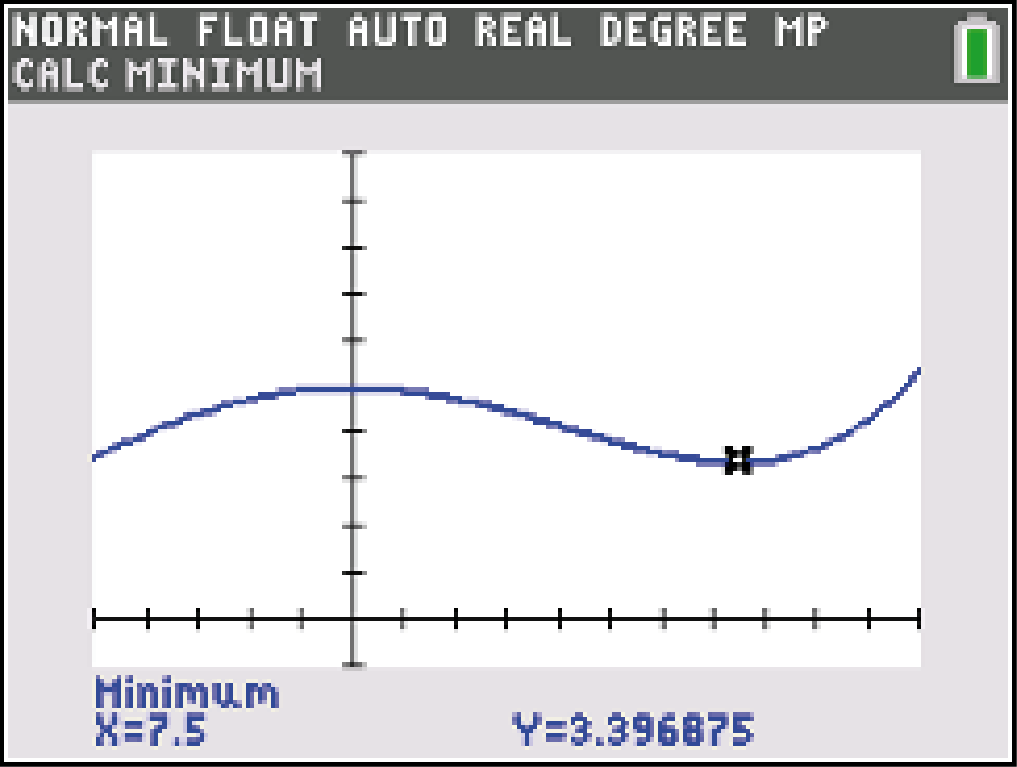Graph mit Minimum bei X=7.5 und Y=3.396875, dargestellt auf einem Taschenrechner.

Abb. 1: Tiefpunkt

Du musst nun noch die Funktionswerte an den Intervallgrenzen berechnen, um ein mögliches Randextremum zu überprüfen. Dies kannst du mit dem folgenden Befehl deines GTRs tun:

2ND $\to$ TRACE(CALC) $\to$ 1: value

Du erhältst dann:

$f(-4,5)\approx 3,74\quad \( \)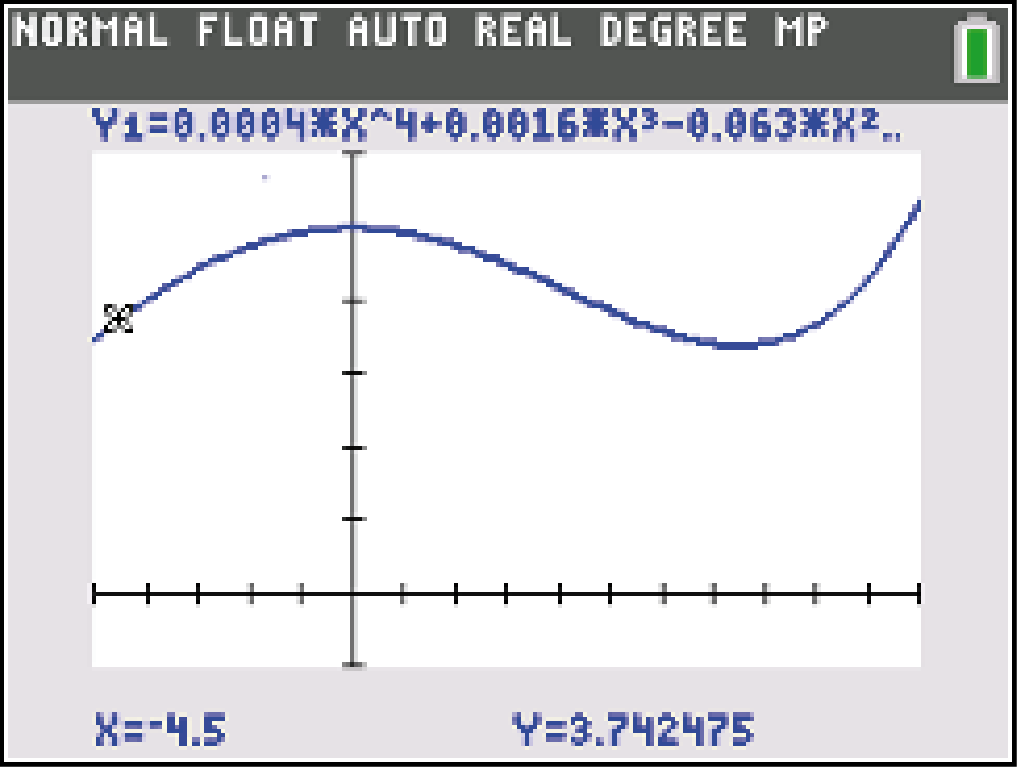

\( \)

f(10,5) \approx 4,77$

Mathematische Grafik mit einer Kurve und Angaben zu X und Y-Werten.

Abb. 2: Intervallgrenzen überprüfen

Beide sind größer als der Funktionswert des lokalen Tiefpunkts, also ist dieser auch der globale Tiefpunkt des angegebenen Intervalls.

Im Modellierungsbereich hat der Tiefpunkt die Koordinaten $T(7,5\mid 4,4)$ .

$\blacktriangleright$ Prozentuale Abweichung angeben

Du sollst angeben, um wie viel Prozent die jeweilige Koordinate von $T(7,5 \mid 3,4)$ von der entsprechenden Koordinate von $Q(7,3\mid 3,3)$ abweicht, also um wie viel Prozent $x_T$ von $x_Q$ und $y_T$ von $y_Q$ abweicht. Nutze dazu die Regeln für die Prozentrechnung.

$\begin{array}[t]{rll} p_x&=& \dfrac{x_T-x_Q}{x_Q} \\[5pt] &=& \dfrac{7,5-7,3}{7,3} \\[5pt] &\approx& 0,027 \\[5pt] &=& 2,7\,\% \\[10pt] p_y&=& \dfrac{y_T-y_Q}{y_Q} \\[5pt] &=& \dfrac{3,4-3,3}{3,3} \\[5pt] &\approx& 0,030 \\[5pt] &=& 3\,\% \\[5pt] \end{array}$

Die $x$ -Koordinate von $T$ weicht um ca. $2,7\,\%$ von der von $Q$ ab, die Abweichung der $y$ -Koordinaten beträgt ca. $3\,\%$ .

(3)

$\blacktriangleright$ Gefälle im Punkt $\boldsymbol{A}$ untersuchen

Der Punkt mit dem stärksten Gefälle ist der Punkt, in dem die Steigung des Graphen minimal ist. Da die erste Ableitung die Steigung des Graphen von $f$ beschreibt, ist dies eine Minimalstelle der ersten Ableitung $f‘$ . Überprüfe also, ob die $x$ -Koordinate von $A$ die Kriterien für eine Minimalstelle $x_M$ von $f‘$ erfüllt.

Notwendiges Kriterium: $f‘‘(x_M)=0$
Hinreichendes Kriterium: $f‘‘‘(x_M) > 0$

Setze dazu zunächst $x_A$ in $f‘‘(x)$ ein und überprüfe, ob das notwendige Kriterium erfüllt wird. Ist dies der Fall, musst du noch das hinreichende Kriterium überprüfen und anschließend begründen, warum die Intervallgrenzen nicht in Frage kommen.

Die ersten beiden Ableitungsfunktionen von $f$ hast du bereits bestimmt. Setze also ein:

$f‘‘(x_A)\approx -0,07\neq 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Das notwendige Kriterium ist nicht erfüllt, also liegt an der Stelle $x =2,7$ keine Minimalstelle von $f‘$ . $A$ kann also nicht der Punkt mit dem steilsten Gefälle sein.

c)

(1)

$\blacktriangleright$ Länge des Seils berechnen

Da das Stahlseil von $A$ nach $P$ geradlinig verläuft, kannst du dessen Länge über den Abstand zwischen den beiden Punkten $A(2,7\mid f(2,7))$ und $P(6,7\mid 7,2)$ berechnen. Die Formel dafür lautet:

$d(P,Q)=$ $\sqrt{(x_Q-x_P)^2 +(y_Q-y_P)^2}$

Setze also ein und beachte anschließend, dass eine Längeneinheit im Koordinatensystem einem Meter entspricht.

$d(A,P)\approx 4,77$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Abstand zwischen $A$ und $P$ beträgt ca. $4,77$ LE, also ist das Stahlseil ca. $4,77\,\text{m}$ lang.

(2)

$\blacktriangleright$ Geradengleichung bestimmen

Du sollst eine Gleichung der Geraden $g$ bestimmen, die durch die Punkte $A$ und $P$ verläuft. Eine Geradengleichung hat allgemein folgende Form:

$g(x)= mx+ b$

Mit Hilfe der Koordinaten der beiden Punkte kannst du ein lineares Gleichungssystem aufstellen, um die Koeffizienten $m$ und $b$ zu berechnen. Berechne dazu zunächst die $y$ -Koordinate $y_A$ von $A$ :

$y_A\approx 4,593$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Damit ergibt sich folgendes Gleichungssystem:

$\begin{array}{} \text{I}\quad&4,593&=& ...\\ \text{II}\quad&7,2&=&...\\ \hline \text{Ia}\quad&-2,607&=&...\\ \quad&0,65175&=&m\\ \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Einsetzen in $\text{II}$ und Auflösen nach $b$ liefert:

$2,833275= b$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Also ist $m\approx 0,652$ und $b\approx 2,833$ . Eine Gleichung der Modellierungsgerade lautet:

$g(x)=0,652x+2,833$

$\blacktriangleright$ Winkelgröße berechnen

Gesucht ist hier die Größe des Steigungswinkels $\alpha$ der Gerade $g$ . Diesen kannst du mit Hilfe der Steigung $m$ der Gerade mit folgender Formel berechnen:

$m = \tan(\alpha)$

Die Steigung von $g$ hast du oben berechnet: $m \approx 0,652$ . Setze also ein und löse nach $\alpha$ auf.

$\begin{array}[t]{rll} m&=& \tan(\alpha) \\[5pt] 0,652&\approx& \tan(\alpha) \\[5pt] \tan^{-1}(0,652)&=&\alpha \\[5pt] 33,1^{\circ}&=& \alpha\\[5pt] \end{array}$

Die Gerade $g$ schließt mit der Horizontalen einen Winkel mit einer ungefähren Größe von $33,1^{\circ}$ ein.

(3)

$\blacktriangleright$ Tangentialen Verlauf überprüfen

Du sollst überprüfen, ob das Seil zwischen $P$ und $E$ tangential zur Dachoberkante verläuft. Beachte dabei, dass die Dachoberkante von der Funktion $f$ modelliert wird, analog zu Aufgabenteil c) (2) kannst du das Seil durch eine Gerade $t$ modellieren. Diese Gerade verläuft tangential zum Graphen von $f$ im Punkt $E$ , wenn folgendes gilt:

$t$ besitzt dieselbe Steigung, wie der Graph von $f$ im Punkt $E$
$t$ verläuft ebenfalls durch den Punkt $E$

Dass der Punkt $E$ auf der Geraden $t$ liegt, ist in der Aufgabenstellung vorausgesetzt. Du musst also nur die Steigungen miteinander vergleichen. Die Steigung des Graphen von $f$ im Punkt $E$ kannst du als $f‘(-2)$ berechnen. Die Steigung der Geraden durch $P$ und $E$ kannst du mit Hilfe folgender Formel berechnen:

$m= \dfrac{y_P-y_E}{x_P-x_E}$

Die Steigung von $t$ ergibt sich daher wie folgt:

$\begin{array}[t]{rll} m_t&=&\dfrac{y_P-y_E}{x_P-x_E} \\[5pt] &=& \dfrac{7,2-4,75}{6,7-(-2)} \\[5pt] &=&\dfrac{49}{174} \\[5pt] \end{array}$

$f‘(-2)= \dfrac{323}{1.250}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Es gilt $m_t \neq f‘(-2)$ , also verläuft das Seil nicht tangential zur Dachoberkante im Punkt $E$ .

d)

(1)

$\blacktriangleright$ Inhalt der Glasfläche berechnen

Die Glasfläche wird nach unten durch die $x$ -Achse, nach links durch die $y$ -Achse und nach oben durch den Graphen der Funktion $h$ begrenzt. Die rechte Grenze ist die Kante durch den Punkt $Q$ , die durch die $x$ -Koordinate von $Q$ also $x =7,3$ beschrieben wird. Du kannst den Inhalt $A$ der Fläche damit als Integral über $h$ in den Grenzen $a=0$ und $b= 7,3$ berechnen. Du kannst das Integral entweder handschriftlich oder mit deinem GTR berechnen.

$\blacktriangleright$ Lösungsweg A: Handschriftlich

$A\approx 27,475$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Glasfläche besitzt eine Größe von ca. $27,475\,\text{m}^2$ .

$\blacktriangleright$ Lösungsweg B: GTR

Du kannst dir den Graphen von $h$ in deinem GTR anzeigen lassen. Ein Integral kannst du dann mit Hilfe des folgenden Befehls berechnen:

2ND $\to$ TRACE (CALC) $\to$ 7

Du erhältst folgendes Ergebnis:

$A = \displaystyle\int_{0}^{7,3}h(x)\;\mathrm dx \approx 27,475$

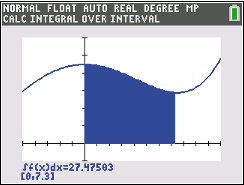Diagramm einer Funktion mit hervorgehobenem Integral über einem Intervall.

Abb. 3: Integralberechnung

Die Glasfläche besitzt eine Größe von ca. $27,475\,\text{m}^2$ .

(2)

$\blacktriangleright$ Lösungsidee angeben

Die Fläche links der $y$ -Achse kann man berechnen, indem man sie in einzelne Teilflächen aufteilt. Für diese Aufteilung gibt es viele verschiedene Möglichkeiten. Auf dem folgenden Bild ist eine dieser Möglichkeiten dargestellt.

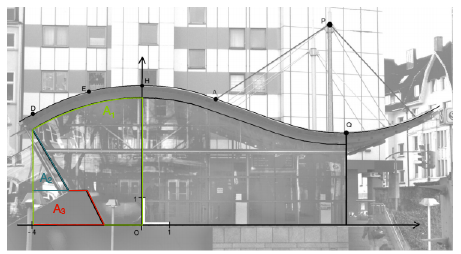Diagramm eines Gebäudes mit geometrischen Formen und Linien, Darstellung von Flächen A1, A2 und A3.

Abb. 4: Aufteilung der Fläche

In diesem Fall setzt sich die gesuchte Fläche aus drei Flächen zusammen. Es kann zuerst der Inhalt $A_1$ der Fläche unter dem Graphen von $h$ im Berecih $a=-4$ bis $b = 0$ mit Hilfe eines Integrals berechnet werden. Von diesem Ergebnis müssen allerdings die Inhalte von zwei Flächen abgezogen werden:

$A_2$ : Der Inhalt der blauen dreieckigen Fläche
$A_3$ : Der Inhalt der roten trapezförmigen Fläche

Für die einzelnen Flächen können dabei folgende Ansätze gemäß der entsprechenden Formeln verwendet werden:

$A_1= \displaystyle\int_{-4}^{0}h(x)\;\mathrm dx$

$A_2 = \frac{1}{2}\cdot g\cdot h$

$A_3 = \frac{1}{2}\cdot (a+b)\cdot h$

Bildnachweise [nach oben]

[1]

© 2016 - SchulLV.

[2]

© 2016 - SchulLV.

[3]

© 2016 - SchulLV.

[4]

© 2016 - SchulLV.

a)

1)

$\blacktriangleright$ Parabelgleichung bestimmen

Du sollst eine Gleichung der Parabel zweiten Grades bestimmen, die durch den Punkt $D(-4\mid 4)$ verläuft und deren Hochpunkt bei $H(0\mid 5)$ liegt. Die allgemeine Funktionsgleichung einer Parabel $p$ zweiten Grades lautet wie folgt:

$p(x) = ax^2 +bx +c$

Mit Hilfe der beiden angegebenen Punkte $D$ und $H$ kannst du ein lineares Gleichungssystem aufstellen, das du nach den Parametern $a$ , $b$ und $c$ lösen kannst. Beachte dabei auch das notwendige Kriterium für einen Hochpunkt an der Stelle $x_E$ :

$p‘(x_E)=0$

Um das Gleichungssystem aufzustellen, benötgist du die erste Ableitung $p‘$ der gesuchten Funktion:

$p‘(x)= 2ax +b$

Nun erhältst du folgende Bedingungen:

$p‘(0)=0$
$p(0)=5$
$p(-4)=4$

Du erhältst folgendes Gleichungssystem:

$\begin{array}{} \text{I}\quad&0&=&2a\cdot 0 +b \\ \text{II}\quad&5&=& a\cdot 0^2 + b\cdot 0 + c\\ \text{III}\quad&4&=& a (-4)^2 + b(-4) +c\\ \end{array}$

Aus $\text{I}$ erhältst du direkt $b = 0$ und aus $\text{II}$ folgt $c = 5$ . Setze diese Ergebnisse noch in $\text{III}$ ein, um $a$ zu berechnen:

$a = \dfrac{-1}{16}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Eine Gleichung der gesuchten Parabel lautet $p(x) = -\dfrac{1}{16}x^2 +5$ .

$\blacktriangleright$ Punktprobe

Um zu überprüfen, ob der Punkt $E(-2\mid 4,75)$ auf der Parabel liegt, setze die Koordinaten in die oben bestimmte Funktionsgleichung ein:

$\begin{array}[t]{rll} p(x)&=& -\dfrac{1}{16}x^2 +5\\[5pt] 4,75&=& -\dfrac{1}{16}\cdot (-2)^2 +5 \\[5pt] 4,75&=&4,75 \\[5pt] \end{array}$

Also liegt der Punkt $E$ auf der Parabel.

(2)

$\blacktriangleright$ Grad der Funktion begründen

Du sollst begründen, dass eine geeignete Funktion zur Modellierung der gesamten Dachoberkante mindestens den Grad drei haben muss. Untersuche den Graphen dafür auf markante Punkte wie Hoch- oder Tiefpunkte und überlege dir, wie viele solcher Punkte eine Funktion mit geringerem Grad höchstens haben kann.

Der Abbildung kannst du entnehmen, dass die Linie der Dachkante einen lokalen Hochpunkt, aber auch einen lokalen Tiefpunkt besitzt. Der Graph einer Funktion zweiten Grades kann aber nur einen lokalen Extrempunkt besitzen und der einer linearen Funktion (Grad eins) besitzt keinen solchen Punkt. Daher muss die Funktion mindestens den Grad drei haben.

b)

(1)

$\blacktriangleright$ Hochpunkt nachweisen

Deine Aufgabe ist es, nachzuweisen, dass der Punkt $H(0\mid 5)$ auch ein Hochpunkt des Graphen von $f$ ist. Beachte dabei die beiden Kriterien für einen Hochpunkt an der Stelle $x_H$ :

Notwendiges Kriterium: $f‘(x_H)=0$
Hinreichendes Kriterium: $f‘‘(x_H)< 0$

Du kannst also wie folgt vorgehen:

Bestimme die ersten beiden Ableitungsfunktionen von $f$ .
Überprüfe das notwendige Kriterium, indem du $f‘(0)$ berechnest.
Überprüfe das hinreichende Kriterium durch Einsetzen in die zweite Ableitungsfunktion.
Überprüfe die $y$ -Koordinate durch Einsetzen in $f(x)$ .

1. Schritt: Ableitungen bilden

Bilde die Ableitungen mit den dir bekannten Ableitungsregeln:

\( \)

\begin{array}[t]{rll} f(x)&=&... \\[10pt] f‘(x)&=&... \\[10pt] f‘‘(x)&=&... \\[5pt] \end{array} \( \)

\( \)

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

2. Schritt: Notwendiges Kriterium überprüfen

Setze $x_H =0$ in $f‘(x)$ ein:

$f‘(x_H)=f‘(0)=0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

3. Schritt: Hinreichendes Kriterium überprüfen

Einsetzen in $f‘‘(x)$ liefert:

$f‘‘(x_H)= f‘‘(0)=0,126 \neq 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

4. Schritt: Koordinaten überprüfen

Einsetzen in $f(x)$ liefert:

$f(x_H)=f(0)=5$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Also ist $H(0\mid 5)$ ebenfalls ein Hochpunkt des Graphen von $f$ .

(2)

$\blacktriangleright$ Tiefpunkt bestimmen

Die Koordinaten des Tiefpunkts kannst du entweder mit Hilfe deines GTRs oder handschriftlich über die Kriterien für einen Tiefpunkt an der Stelle $x_T$ bestimmen:

Notwendiges Kriterium: $f‘(x_T)=0$
Hinreichendes Kriterium: $f‘‘(x_T)> 0$

Beachte, dass du auch die Intervallgrenzen auf mögliche Randextrema überprüfen musst.

$\blacktriangleright$ Lösungsweg A: Handschriftlich

Du kannst wie folgt vorgehen:

Wende das notwendige Kriterium an, indem du $f‘(x)=0$ setzt und so mögliche Extremstellen bestimmst.
Überprüfe das hinreichende Kriterium durch Einsetzen in die zweite Ableitungsfunktion.
Berechne die $y$ -Koordinate des Tiefpunkts durch Einsetzen in $f(x)$ .
Berechne die Funktionswerte an den Intervallgrenzen um mögliche Randextrema auszuschließen.

1. Schritt: Notwendiges Kriterium anwenden

$x_1 = 0$ und $x^2 +3x-78,75= 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Du kannst nun die p-q-Formel anwenden, um weitere Lösungen der Gleichung zu bestimmen:

$\begin{array}[t]{rll} x_2&=&-\dfrac{3}{2} + 9 \\[5pt] &=& 7,5 \\[10pt] x_3&=& -\dfrac{3}{2} - 9 \\[5pt] &=& -10,5 \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Für die Modellierung ist nur der Bereich $-4,5 \leq x \leq 10,5$ relevant, also fällt $x_3$ aus der Betrachtung raus. Bei $x_1$ handelt es sich laut Abbildung um eine Maximalstelle.

2. Schritt: Hinreichendes Kriterium überprüfen

Einsetzen von $x_2=7,5$ in $f‘‘(x)$ liefert:

$\begin{array}[t]{rll} f‘‘(x_2)&=&f‘‘(7,5) \\[5pt] &=& 0,216 > 0 \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

An der Stelle $x_2 = 7,5$ besitzt der Graph von $f$ einen lokalen Tiefpunkt.

3. Schritt: Funktionswert berechnen

Die $y$ -Koordinate des lokalen Tiefpunkts erhältst du durch Einsetzen von $x_2$ in $f(x)$ :

$y_T \approx 3,40$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

4. Schritt: Intervallgrenzen überprüfen

Überprüfe die Grenzen des Modellierungsbereichs $x_0 = -4,5$ und $x_4 = 10,5$ auf Randextrema.

$\begin{array}[t]{rll} f(-4,5)&\approx &3,74 \, > \, 3,4 \\[10pt] f(10,5)&\approx& 4,77 \, > \, 3,4\\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Funktiuonswerte an den Intervallgrenzen sind größer als der Funktionswert des lokalen Tiefpunkts. Damit ist der lokale Tiefpunkt mit den gerundeten Koordinaten $T(7,5\mid 4,4)$ auch der Tiefpunkt des gesamten Modellierungsbereichs.

$\blacktriangleright$ Lösungsweg B: GTR

Mit deinem GTR kannst du einen lokalen Tiefpunkt bestimmen, indem du dir den Graphen von $f$ anzeigen lässt. Den Befehl für einen Tiefpunkt findest du dann unter:

Shift $\to$ F5 (G-Solv) $\to$ F3 (Min)

Du erhältst folgendes gerundetes Ergebnis:

$T(7,5\mid 4,4)$

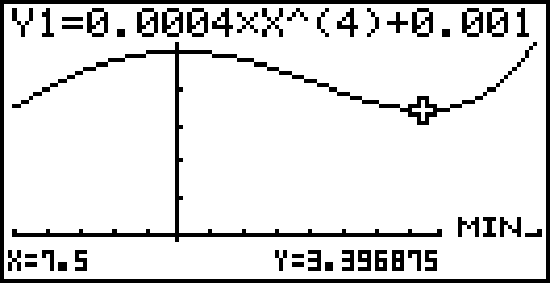Grafik einer mathematischen Funktion mit x- und y-Achse, zeigt einen Punkt mit Koordinaten x=7.5 und y=3.396875.

Abb. 1: Tiefpunkt

Du musst nun noch die Funktionswerte an den Intervallgrenzen berechnen, um ein mögliches Randextremum zu überprüfen. Dies kannst du mit dem folgenden Befehl deines GTRs tun:

Shift $\to$ F5 (G-Solv) $\to$ F6 $\to$ F1 (Y-Cal)

Du erhältst dann:

$f(-4,5)\approx 3,74\quad \( \)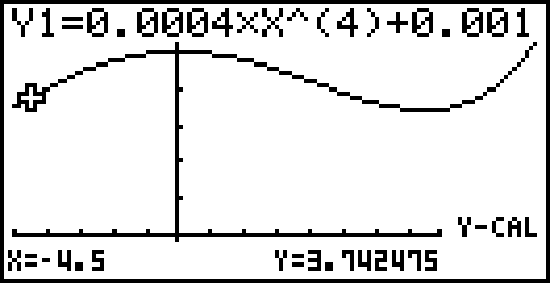

\( \)

f(10,5) \approx 4,77$

Grafik mit mathematischer Funktion und Koordinatenachsen. Darstellung einer Kurve und Werte für x und y.

Abb. 2: Intervallgrenzen überprüfen

Beide sind größer als der Funktionswert des lokalen Tiefpunkts, also ist dieser auch der globale Tiefpunkt des angegebenen Intervalls.

Im Modellierungsbereich hat der Tiefpunkt die Koordinaten $T(7,5\mid 4,4)$ .

$\blacktriangleright$ Prozentuale Abweichung angeben

Du sollst angeben, um wie viel Prozent die jeweilige Koordinate von $T(7,5 \mid 3,4)$ von der entsprechenden Koordinate von $Q(7,3\mid 3,3)$ abweicht, also um wie viel Prozent $x_T$ von $x_Q$ und $y_T$ von $y_Q$ abweicht. Nutze dazu die Regeln für die Prozentrechnung.

$\begin{array}[t]{rll} p_x&=& \dfrac{x_T-x_Q}{x_Q} \\[5pt] &=& \dfrac{7,5-7,3}{7,3} \\[5pt] &\approx& 0,027 \\[5pt] &=& 2,7\,\% \\[10pt] p_y&=& \dfrac{y_T-y_Q}{y_Q} \\[5pt] &=& \dfrac{3,4-3,3}{3,3} \\[5pt] &\approx& 0,030 \\[5pt] &=& 3\,\% \\[5pt] \end{array}$

Die $x$ -Koordinate von $T$ weicht um ca. $2,7\,\%$ von der von $Q$ ab, die Abweichung der $y$ -Koordinaten beträgt ca. $3\,\%$ .

(3)

$\blacktriangleright$ Gefälle im Punkt $\boldsymbol{A}$ untersuchen

Der Punkt mit dem stärksten Gefälle ist der Punkt, in dem die Steigung des Graphen minimal ist. Da die erste Ableitung die Steigung des Graphen von $f$ beschreibt, ist dies eine Minimalstelle der ersten Ableitung $f‘$ . Überprüfe also, ob die $x$ -Koordinate von $A$ die Kriterien für eine Minimalstelle $x_M$ von $f‘$ erfüllt.

Notwendiges Kriterium: $f‘‘(x_M)=0$
Hinreichendes Kriterium: $f‘‘‘(x_M) > 0$

Setze dazu zunächst $x_A$ in $f‘‘(x)$ ein und überprüfe, ob das notwendige Kriterium erfüllt wird. Ist dies der Fall, musst du noch das hinreichende Kriterium überprüfen und anschließend begründen, warum die Intervallgrenzen nicht in Frage kommen.

Die ersten beiden Ableitungsfunktionen von $f$ hast du bereits bestimmt. Setze also ein:

$f‘‘(x_A)\approx -0,07\neq 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Das notwendige Kriterium ist nicht erfüllt, also liegt an der Stelle $x =2,7$ keine Minimalstelle von $f‘$ . $A$ kann also nicht der Punkt mit dem steilsten Gefälle sein.

c)

(1)

$\blacktriangleright$ Länge des Seils berechnen

Da das Stahlseil von $A$ nach $P$ geradlinig verläuft, kannst du dessen Länge über den Abstand zwischen den beiden Punkten $A(2,7\mid f(2,7))$ und $P(6,7\mid 7,2)$ berechnen. Die Formel dafür lautet:

$d(P,Q)=$ $\sqrt{(x_Q-x_P)^2 +(y_Q-y_P)^2}$

Setze also ein und beachte anschließend, dass eine Längeneinheit im Koordinatensystem einem Meter entspricht.

$d(A,P)\approx 4,77$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Abstand zwischen $A$ und $P$ beträgt ca. $4,77$ LE, also ist das Stahlseil ca. $4,77\,\text{m}$ lang.

(2)

$\blacktriangleright$ Geradengleichung bestimmen

Du sollst eine Gleichung der Geraden $g$ bestimmen, die durch die Punkte $A$ und $P$ verläuft. Eine Geradengleichung hat allgemein folgende Form:

$g(x)= mx+ b$

Mit Hilfe der Koordinaten der beiden Punkte kannst du ein lineares Gleichungssystem aufstellen, um die Koeffizienten $m$ und $b$ zu berechnen. Berechne dazu zunächst die $y$ -Koordinate $y_A$ von $A$ :

$y_A\approx 4,593$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Damit ergibt sich folgendes Gleichungssystem:

$\begin{array}{} \text{I}\quad&4,593&=& ...\\ \text{II}\quad&7,2&=&...\\ \hline \text{Ia}\quad&-2,607&=&...\\ \quad&0,65175&=&m\\ \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Einsetzen in $\text{II}$ und Auflösen nach $b$ liefert:

$2,833275= b$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Also ist $m\approx 0,652$ und $b\approx 2,833$ . Eine Gleichung der Modellierungsgerade lautet:

$g(x)=0,652x+2,833$

$\blacktriangleright$ Winkelgröße berechnen

Gesucht ist hier die Größe des Steigungswinkels $\alpha$ der Gerade $g$ . Diesen kannst du mit Hilfe der Steigung $m$ der Gerade mit folgender Formel berechnen:

$m = \tan(\alpha)$

Die Steigung von $g$ hast du oben berechnet: $m \approx 0,652$ . Setze also ein und löse nach $\alpha$ auf.

$\begin{array}[t]{rll} m&=& \tan(\alpha) \\[5pt] 0,652&\approx& \tan(\alpha) \\[5pt] \tan^{-1}(0,652)&=&\alpha \\[5pt] 33,1^{\circ}&=& \alpha\\[5pt] \end{array}$

Die Gerade $g$ schließt mit der Horizontalen einen Winkel mit einer ungefähren Größe von $33,1^{\circ}$ ein.

(3)

$\blacktriangleright$ Tangentialen Verlauf überprüfen

Du sollst überprüfen, ob das Seil zwischen $P$ und $E$ tangential zur Dachoberkante verläuft. Beachte dabei, dass die Dachoberkante von der Funktion $f$ modelliert wird, analog zu Aufgabenteil c) (2) kannst du das Seil durch eine Gerade $t$ modellieren. Diese Gerade verläuft tangential zum Graphen von $f$ im Punkt $E$ , wenn folgendes gilt:

$t$ besitzt dieselbe Steigung, wie der Graph von $f$ im Punkt $E$
$t$ verläuft ebenfalls durch den Punkt $E$

Dass der Punkt $E$ auf der Geraden $t$ liegt, ist in der Aufgabenstellung vorausgesetzt. Du musst also nur die Steigungen miteinander vergleichen. Die Steigung des Graphen von $f$ im Punkt $E$ kannst du als $f‘(-2)$ berechnen. Die Steigung der Geraden durch $P$ und $E$ kannst du mit Hilfe folgender Formel berechnen:

$m= \dfrac{y_P-y_E}{x_P-x_E}$

Die Steigung von $t$ ergibt sich daher wie folgt:

$\begin{array}[t]{rll} m_t&=&\dfrac{y_P-y_E}{x_P-x_E} \\[5pt] &=& \dfrac{7,2-4,75}{6,7-(-2)} \\[5pt] &=&\dfrac{49}{174} \\[5pt] \end{array}$

$f‘(-2)= \dfrac{323}{1.250}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Es gilt $m_t \neq f‘(-2)$ , also verläuft das Seil nicht tangential zur Dachoberkante im Punkt $E$ .

d)

(1)

$\blacktriangleright$ Inhalt der Glasfläche berechnen

Die Glasfläche wird nach unten durch die $x$ -Achse, nach links durch die $y$ -Achse und nach oben durch den Graphen der Funktion $h$ begrenzt. Die rechte Grenze ist die Kante durch den Punkt $Q$ , die durch die $x$ -Koordinate von $Q$ also $x =7,3$ beschrieben wird. Du kannst den Inhalt $A$ der Fläche damit als Integral über $h$ in den Grenzen $a=0$ und $b= 7,3$ berechnen. Du kannst das Integral entweder handschriftlich oder mit deinem GTR berechnen.

$\blacktriangleright$ Lösungsweg A: Handschriftlich

$A\approx 27,475$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Glasfläche besitzt eine Größe von ca. $27,475\,\text{m}^2$ .

$\blacktriangleright$ Lösungsweg B: GTR

Du kannst dir den Graphen von $h$ in deinem GTR anzeigen lassen. Ein Integral kannst du dann mit Hilfe des folgenden Befehls berechnen:

F5 (G-SOLV) $\to$ F6 ( $\triangleright$ ) $\to$ F3

Du erhältst folgendes Ergebnis:

$A = \displaystyle\int_{0}^{7,3}h(x)\;\mathrm dx \approx 27,475$

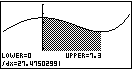Diagramm mit einer Kurve und schattiertem Bereich zwischen den Werten 0 und 7,3.

Abb. 3: Integralberechnung

Die Glasfläche besitzt eine Größe von ca. $27,475\,\text{m}^2$ .

(2)

$\blacktriangleright$ Lösungsidee angeben

Die Fläche links der $y$ -Achse kann man berechnen, indem man sie in einzelne Teilflächen aufteilt. Für diese Aufteilung gibt es viele verschiedene Möglichkeiten. Auf dem folgenden Bild ist eine dieser Möglichkeiten dargestellt.

Diagramm eines Gebäudes mit geometrischen Formen und Linien, Darstellung von Flächen A1, A2 und A3.

Abb. 4: Aufteilung der Fläche

In diesem Fall setzt sich die gesuchte Fläche aus drei Flächen zusammen. Es kann zuerst der Inhalt $A_1$ der Fläche unter dem Graphen von $h$ im Berecih $a=-4$ bis $b = 0$ mit Hilfe eines Integrals berechnet werden. Von diesem Ergebnis müssen allerdings die Inhalte von zwei Flächen abgezogen werden:

$A_2$ : Der Inhalt der blauen dreieckigen Fläche
$A_3$ : Der Inhalt der roten trapezförmigen Fläche

Für die einzelnen Flächen können dabei folgende Ansätze gemäß der entsprechenden Formeln verwendet werden:

$A_1= \displaystyle\int_{-4}^{0}h(x)\;\mathrm dx$

$A_2 = \frac{1}{2}\cdot g\cdot h$

$A_3 = \frac{1}{2}\cdot (a+b)\cdot h$

Bildnachweise [nach oben]

[1]

© 2016 - SchulLV.

[2]

© 2016 - SchulLV.

[3]

© 2016 - SchulLV.

[4]

© 2016 - SchulLV.