Aufgabe 1
Aufgabenstellung
Ein Schüler beobachtet in einem Experiment insgesamt sechs Tage lang die Vermehrung von Pantoffeltierchen in einer Nährlösung. Zur Modellierung der Anzahl der Pantoffeltierchen während der ersten drei Tage verwendet er für  die Funktion
die Funktion  mit der Gleichung
mit der Gleichung
 ,
,  .
Dabei wird
.
Dabei wird  als Maßzahl zur Einheit 1 Tag und
als Maßzahl zur Einheit 1 Tag und  als Anzahl der Pantoffeltierchen zum Zeitpunkt
als Anzahl der Pantoffeltierchen zum Zeitpunkt  aufgefasst.
Der Graph von
aufgefasst.
Der Graph von  ist in der Abbildung dargestellt.
ist in der Abbildung dargestellt.
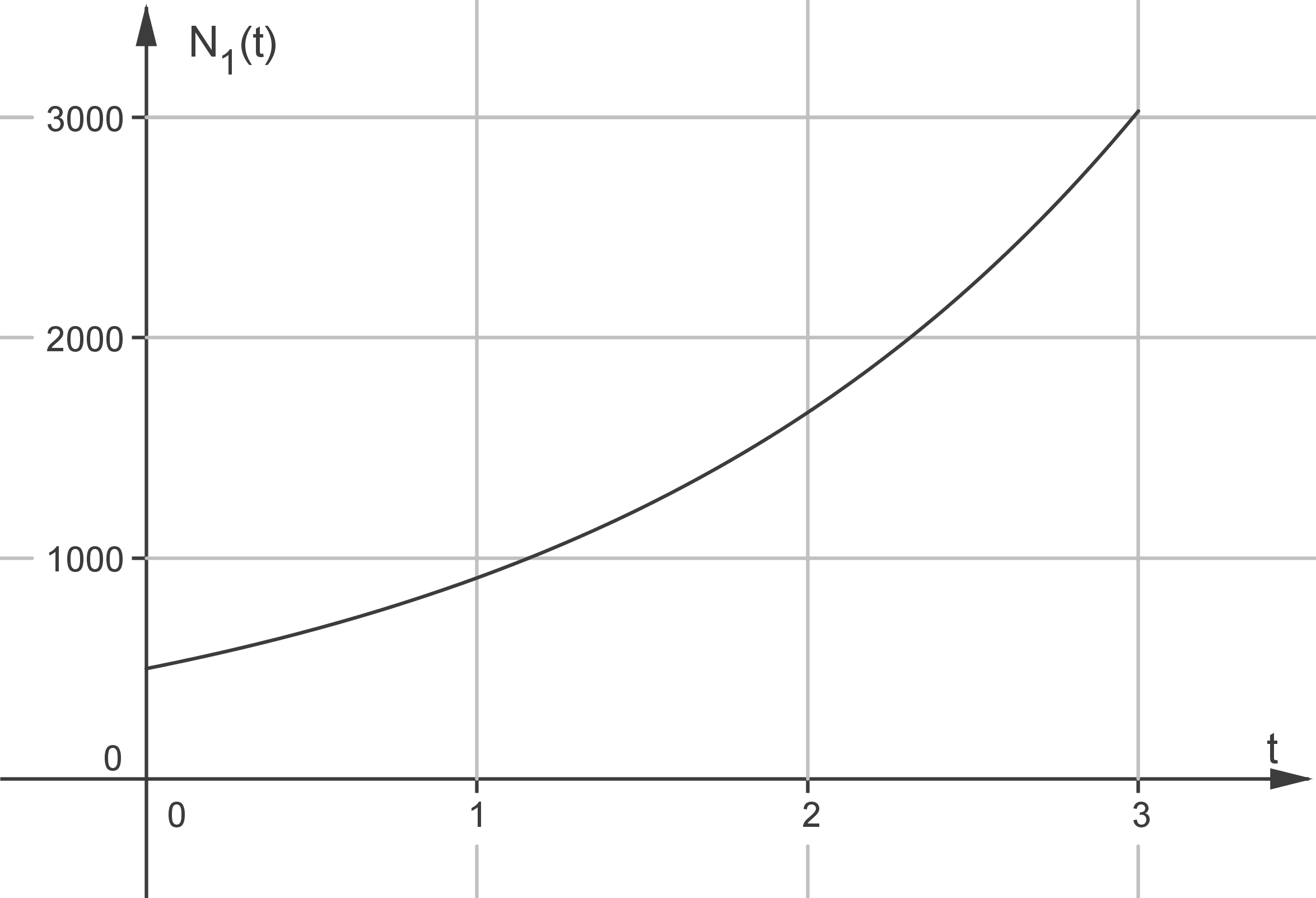 Abbildung
Abbildung
 ) wird im Modell des Schülers die momentane Änderungsrate der Anzahl der Pantoffeltierchen durch die Funktion
) wird im Modell des Schülers die momentane Änderungsrate der Anzahl der Pantoffeltierchen durch die Funktion  mit der Gleichung
mit der Gleichung
 ,
,  ,
beschrieben.
,
beschrieben.
Dabei wird als Maßzahl zur Einheit 1 Tier pro Tag aufgefasst.
als Maßzahl zur Einheit 1 Tier pro Tag aufgefasst.
 Abbildung
Abbildung
a) (1) Berechne den Funktionswert von  an der Stelle
an der Stelle  und interpretiere diesen Wert im Sachzusammenhang.
und interpretiere diesen Wert im Sachzusammenhang.
(3P)
(2) Bestimme rechnerisch den Zeitpunkt, zu dem  Pantoffeltierchen in der Nährlösung vorhanden sind.
Pantoffeltierchen in der Nährlösung vorhanden sind.
(4P)
(3) Berechne, um wie viele Tiere pro Tag die Anzahl der Pantoffeltierchen in der Nährlösung während der ersten drei Tage durchschnittlich wächst.
(3P)
(4) Begründe, warum eine Funktion mit dem Funktionsterm  nur für einen begrenzten Zeitraum zur Modellierung der Anzahl der Pantoffeltierchen geeignet ist.
nur für einen begrenzten Zeitraum zur Modellierung der Anzahl der Pantoffeltierchen geeignet ist.
(4P)
Während der ersten drei Tage (für Dabei wird
b) Für die Funktion  und die zugehörige Ableitungsfunktion
und die zugehörige Ableitungsfunktion  gilt für alle
gilt für alle  die Aussage:
die Aussage:
 und
und  [Die Gültigkeit dieser Aussage musst du nicht nachweisen.]
[Die Gültigkeit dieser Aussage musst du nicht nachweisen.]
Interpretiere die Bedeutung dieser Aussage im Sachzusammenhang.
Interpretiere die Bedeutung dieser Aussage im Sachzusammenhang.
(6P)
c) Bei der weiteren Beobachtung erkennt der Schüler, dass nach etwa drei Tagen die momentane Änderungsrate der Anzahl der Pantoffeltierchen geringer wird. Zur Modellierung der momentanen Änderungsrate der Anzahl der Pantoffeltierchen nach dem dritten Tag bis zum Ende der Beobachtung (also für  ) verwendet der Schüler die Funktion
) verwendet der Schüler die Funktion  mit der Gleichung
mit der Gleichung
 ,
,  .
Dabei wird
.
Dabei wird  als Maßzahl zur Einheit 1 Tier pro Tag aufgefasst.
als Maßzahl zur Einheit 1 Tier pro Tag aufgefasst.
(1) Zeige, dass für die Funktionen  und
und  für alle
für alle  die Gleichung
die Gleichung  gilt.
gilt.
(5P)
(2) Interpretiere die Bedeutung der Gleichung  für
für  im Sachzusammenhang.
im Sachzusammenhang.
(4P)
(3) Zeige, dass die Funktion  mit der Gleichung
mit der Gleichung  eine Stammfunktion der Funktion
eine Stammfunktion der Funktion  mit der Gleichung
mit der Gleichung  ist.
ist.
(4P)
(4) Bestimme, wie viele Pantoffeltierchen in der Nährlösung im Laufe des vierten Tages (d. h. im Intervall ![\([3;4]\)](https://mathjax.schullv.de/4b5b20a598c380c75e8acf7b8085c3d1a345173dbfca85eaed96165c79c838f7?color=5a5a5a) ) hinzukommen, wenn die momentane Änderungsrate der Anzahl der Pantoffeltierchen für
) hinzukommen, wenn die momentane Änderungsrate der Anzahl der Pantoffeltierchen für  durch die Funktion
durch die Funktion  beschrieben wird.
beschrieben wird.
(6P)
(5) Ermittle ausgehend von den Funktionen  und
und  eine Gleichung der Funktion
eine Gleichung der Funktion  , durch die die Anzahl der Pantoffeltierchen nach dem dritten Tag bis zum Ende der Beobachtung beschrieben werden kann.
, durch die die Anzahl der Pantoffeltierchen nach dem dritten Tag bis zum Ende der Beobachtung beschrieben werden kann.
[Zur Kontrolle: ]
]
[Zur Kontrolle:
(7P)
(6) Der Schüler verwendet die Funktion  auch zur Modellierung der Anzahl der Pantoffeltierchen für
auch zur Modellierung der Anzahl der Pantoffeltierchen für  .
.
Begründe, dass in diesem Modell die Anzahl der Pantoffeltierchen in der Nährlösung zu keinem Zeitpunkt größer als wird.
wird.
Begründe, dass in diesem Modell die Anzahl der Pantoffeltierchen in der Nährlösung zu keinem Zeitpunkt größer als
(4P)
a) (1)
 Funktionswert berechnen und Interpretation im Sachzusammenhang
Deine Aufgabe ist es hier, den Funktionswert von
Funktionswert berechnen und Interpretation im Sachzusammenhang
Deine Aufgabe ist es hier, den Funktionswert von  an der Stelle
an der Stelle  zu berechnen. Setze dazu
zu berechnen. Setze dazu  in die Funktionsgleichung
in die Funktionsgleichung  ein:
ein:
 Nun ist noch danach gefragt, den Funktionswert zu interpretieren.
Nun ist noch danach gefragt, den Funktionswert zu interpretieren.  wird als Anzahl der Pantoffeltierchen zum Zeitpunkt
wird als Anzahl der Pantoffeltierchen zum Zeitpunkt  aufgefasst, wobei
aufgefasst, wobei  als Maßzahl zur Einheit
als Maßzahl zur Einheit  Tag aufgefasst wird. Somit beschreibt
Tag aufgefasst wird. Somit beschreibt  die Anzahl der Pantoffeltierchen nach
die Anzahl der Pantoffeltierchen nach  Tagen.
(2)
Tagen.
(2)
 Zeitpunkt, zu dem
Zeitpunkt, zu dem  Pantoffeltierchen vorhanden sind, berechnen
Hier ist nach dem Zeitpunkt gefragt, zu dem
Pantoffeltierchen vorhanden sind, berechnen
Hier ist nach dem Zeitpunkt gefragt, zu dem  Pantoffeltierchen in der Nährlösung vorhanden sind. Also ist nach dem
Pantoffeltierchen in der Nährlösung vorhanden sind. Also ist nach dem  gesucht, für das
gesucht, für das  gilt. Setze dazu den Funktionsterm mit
gilt. Setze dazu den Funktionsterm mit  gleich und löse nach
gleich und löse nach  auf:
auf:
![\(\begin{array}[t]{rll}
N_1(t)&=2.000 & \quad \\[5pt]
500 \cdot \mathrm e^{0,6 \cdot t}&=2.000 & \quad \mid\; :500 \\[5pt]
\mathrm e^{0,6 \cdot t}&=4 & \quad \mid\; \ln \\[5pt]
0,6 \cdot t &= \ln(4) &\quad \mid\; :0,6 \\[5pt]
t&=\dfrac{\ln(4)}{0,6} \\[5pt]
&\approx 2,31
\end{array}\)](https://mathjax.schullv.de/5634c6e48e8c9c1921e5086d65df7c7a96274ca92709b33526b0414fc283626f?color=5a5a5a) Also sind nach ca.
Also sind nach ca.  Tagen
Tagen  Pantoffeltierchen in der Nährlösung vorhanden.
(3)
Pantoffeltierchen in der Nährlösung vorhanden.
(3)
 Durchschnittliches Wachstum der Anzahl der Pantoffeltierchen
Das durchschnittliche Wachstum an den ersten drei Tagen berechnest du, indem du die Anzahl an neu dazugekommenen Pantoffeltierchen durch die Anzahl an vergangenen Tagen teilst. Die Anzahl der neu dazugekommenen Pantoffeltierchen ist die Differenz von Pantoffeltierchen zu Beginn und der Pantoffeltierchen nach 3 Tagen, also
Durchschnittliches Wachstum der Anzahl der Pantoffeltierchen
Das durchschnittliche Wachstum an den ersten drei Tagen berechnest du, indem du die Anzahl an neu dazugekommenen Pantoffeltierchen durch die Anzahl an vergangenen Tagen teilst. Die Anzahl der neu dazugekommenen Pantoffeltierchen ist die Differenz von Pantoffeltierchen zu Beginn und der Pantoffeltierchen nach 3 Tagen, also  . Damit erhältst du:
. Damit erhältst du:
 Das durchschnittliche Wachstum der Pantoffeltierchen an den ersten drei Tagen beträgt 841,61 Tierchen pro Tag.
(4)
Das durchschnittliche Wachstum der Pantoffeltierchen an den ersten drei Tagen beträgt 841,61 Tierchen pro Tag.
(4)
 Begründen, warum die Funktion nur für einen begrenzten Zeitraum geeignet ist
Eine Funktion mit dem Funktionsterm
Begründen, warum die Funktion nur für einen begrenzten Zeitraum geeignet ist
Eine Funktion mit dem Funktionsterm  beschreibt exponentielles Wachstum. Der Grenzwert einer solchen Funktion ist "
beschreibt exponentielles Wachstum. Der Grenzwert einer solchen Funktion ist " ". Nach einem begrenzten Zeitraum wird die Anzahl der Pantoffeltierchen wegen des beschränkten Platz- und Nahrungsangebot in der Nährlösung jedoch nicht weiter unbeschränkt wachsen. Das unbeschränkte Wachstum steht somit im Widerspruch zu dem beschränkten Platz- und Nahrungsangebot. Damit ist eine solche Funktion nur für einen begrenzten Zeitraum für das Experiment geeignet.
". Nach einem begrenzten Zeitraum wird die Anzahl der Pantoffeltierchen wegen des beschränkten Platz- und Nahrungsangebot in der Nährlösung jedoch nicht weiter unbeschränkt wachsen. Das unbeschränkte Wachstum steht somit im Widerspruch zu dem beschränkten Platz- und Nahrungsangebot. Damit ist eine solche Funktion nur für einen begrenzten Zeitraum für das Experiment geeignet.
b)
 Interpretation im Sachzusammenhang
Der erste Teil der Aussage lautet
Interpretation im Sachzusammenhang
Der erste Teil der Aussage lautet  . Dies bedeutet, dass die momentane Änderungsrate zu jedem Zeitpunkt echt größer 0 ist. Also steigt die Anzahl der Tierchen immer weiter an.
Der zweite Teil der Aussage lautet
. Dies bedeutet, dass die momentane Änderungsrate zu jedem Zeitpunkt echt größer 0 ist. Also steigt die Anzahl der Tierchen immer weiter an.
Der zweite Teil der Aussage lautet  . Die Ableitung von
. Die Ableitung von  , also
, also  , beschreibt die Änderungsrate von
, beschreibt die Änderungsrate von  . Diese ist positiv, daher nimmt
. Diese ist positiv, daher nimmt  mit der Zeit größer werdende Werte an. Dies bedeutet im Sachzusammenhang, dass der Anstieg der Anzahl der Tierchen immer größer wird.
Insgesamt lässt sich sagen, dass die Anzahl der Pantoffeltierchen zu jeder Zeit steigt und dieser Anstieg immer größer wird.
mit der Zeit größer werdende Werte an. Dies bedeutet im Sachzusammenhang, dass der Anstieg der Anzahl der Tierchen immer größer wird.
Insgesamt lässt sich sagen, dass die Anzahl der Pantoffeltierchen zu jeder Zeit steigt und dieser Anstieg immer größer wird.
c) (1)
 Gleichheit zeigen
Berechne jeweils die beiden Funktionswerte, um die Gleichheit zu zeigen. Setze dazu
Gleichheit zeigen
Berechne jeweils die beiden Funktionswerte, um die Gleichheit zu zeigen. Setze dazu  in die Funktionsgleichung von
in die Funktionsgleichung von  ein bzw.
ein bzw.  in die Funktionsgleichung von
in die Funktionsgleichung von  ein:
ein:

 Damit ist gezeigt, dass für alle
Damit ist gezeigt, dass für alle  die Gleichung gilt.
(2)
die Gleichung gilt.
(2)
 Interpretation im Sachzusammenhang
Die Gleichung
Interpretation im Sachzusammenhang
Die Gleichung  bedeutet, dass die Änderungsraten der Anzahl der Pantoffeltierchen zu den Zeitpunkten
bedeutet, dass die Änderungsraten der Anzahl der Pantoffeltierchen zu den Zeitpunkten  und
und  gleich sind. Diese beiden Zeitpunkte sind "gleich weit" vom Zeitpunkt
gleich sind. Diese beiden Zeitpunkte sind "gleich weit" vom Zeitpunkt  entfernt. Beispielsweise bedeutet dies, dass die Änderunsrate am zweiten Tag gleich der Änderungsrate am vierten Tag ist (hier ist also
entfernt. Beispielsweise bedeutet dies, dass die Änderunsrate am zweiten Tag gleich der Änderungsrate am vierten Tag ist (hier ist also  ). Also kann man sagen, dass die Änderungsraten symmetrisch um den dritten Tag verteilt sind.
(3)
). Also kann man sagen, dass die Änderungsraten symmetrisch um den dritten Tag verteilt sind.
(3)
 Zeige, dass
Zeige, dass  Stammfunktion von
Stammfunktion von  ist
ist
 ist eine Stammfunktion von
ist eine Stammfunktion von  , wenn die Ableitung von
, wenn die Ableitung von  gerade
gerade  ist, also
ist, also  gilt. Leite dazu
gilt. Leite dazu  ab, beachte dabei die Kettenregel zu verwenden:
ab, beachte dabei die Kettenregel zu verwenden:
![\(\begin{array}[t]{rll}
F(x)&=&-\dfrac{5}{3} \cdot \mathrm e^{3,6 - 0,6 \cdot t} & \quad \scriptsize \\[10pt]
F‘(x)&=&\left(-\dfrac{5}{3}\right) \cdot \mathrm e^{3,6 - 0,6 \cdot x} \cdot \left(-0,6\right)\\[5pt]
&=&\mathrm e^{3,6 - 0,6 \cdot x}\\[5pt]
&=&f(x)
\end{array}\)](https://mathjax.schullv.de/3bcb5dbdf2412683a8d7f46bdc2b1f5d5bec47cbbffef2fdec1c79a0bb2c8d27?color=5a5a5a) Damit hast du gezeigt, dass
Damit hast du gezeigt, dass  eine Stammfunktion von
eine Stammfunktion von  ist.
(4)
ist.
(4)
 Anstieg im Laufe des vierten Tages berechnen
Hier sollst du den Anstieg der Anzahl der Pantoffeltierchen im Laufe des vierten Tages berechnen. Diesen kannst du mit der momentanen Änderungsrate bestimmen. Die momentane Änderungsrate beschreibt hier das Wachstum der Pantoffeltierchen, damit beschreibt das Integral über die Änderungsrate innerhalb eines Zeitintervalls den insgesamten Anstieg der Pantoffeltierchen innerhalb dieses Zeitraums.
Die Anzahl an Pantoffeltierchen, die im Laufe des Tages hinzugekommen sind, ist hier also gerade das Integral über die momentane Änderungsrate
Anstieg im Laufe des vierten Tages berechnen
Hier sollst du den Anstieg der Anzahl der Pantoffeltierchen im Laufe des vierten Tages berechnen. Diesen kannst du mit der momentanen Änderungsrate bestimmen. Die momentane Änderungsrate beschreibt hier das Wachstum der Pantoffeltierchen, damit beschreibt das Integral über die Änderungsrate innerhalb eines Zeitintervalls den insgesamten Anstieg der Pantoffeltierchen innerhalb dieses Zeitraums.
Die Anzahl an Pantoffeltierchen, die im Laufe des Tages hinzugekommen sind, ist hier also gerade das Integral über die momentane Änderungsrate  von den Zeitpunkten
von den Zeitpunkten  bis
bis  . Somit beschreibt das Integral
. Somit beschreibt das Integral  die Anzahl an Tierchen, die im Laufe des vierten Tages dazugekommen sind. Dieses kannst du direkt per Hand oder mit deinem GTR berechnen:
die Anzahl an Tierchen, die im Laufe des vierten Tages dazugekommen sind. Dieses kannst du direkt per Hand oder mit deinem GTR berechnen:
 Lösungsweg A: Lösen per Hand
Lösungsweg A: Lösen per Hand
 In Aufgabenteil (3) hast du bereits gezeigt, dass
In Aufgabenteil (3) hast du bereits gezeigt, dass  eine Stammfunktion von
eine Stammfunktion von  ist. Somit kannst du hier den Hauptsatz der Integralrechnung anwenden:
ist. Somit kannst du hier den Hauptsatz der Integralrechnung anwenden:
![\(\begin{array}[t]{rll}
300 \cdot \displaystyle\int_{3}^{4} f(t)\; \mathrm dt &= 300 \cdot \left(F(4) - F(3)\right) \\[5pt]
&= 300 \cdot \left( \left(-\dfrac{5}{3}\right) \cdot \mathrm e^{3,6 - 0,6 \cdot 4} - \left(-\dfrac{5}{3}\right) \cdot \mathrm e^{3,6 - 0,6 \cdot 3}\right) \\[5pt]
&= 300 \cdot \left( \dfrac{5}{3} \cdot \mathrm e^{1,8} -\dfrac{5}{3} \cdot \mathrm e^{1,2} \right) \\[5pt]
&= 300 \cdot \dfrac{5}{3} \cdot \left( \mathrm e^{1,8} - \mathrm e^{1,2}\right)\\[5pt]
&= 500 \cdot \left( \mathrm e^{1,8} - \mathrm e^{1,2}\right) \\[5pt]
&\approx 1.364,77
\end{array}\)](https://mathjax.schullv.de/13ee43ef88b166ec036cc1276f0b6c910247528bfc2e1177099e6745f6261132?color=5a5a5a) Der Anstieg im Laufe des vierten Tages beträgt also ca.
Der Anstieg im Laufe des vierten Tages beträgt also ca.  Pantoffeltierchen.
Pantoffeltierchen.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort eingegeben, dann passe das Fenster so an, dass du den gewünschten Bereich sehen kannst.
Bestimme dann über
. Hast du diesen dort eingegeben, dann passe das Fenster so an, dass du den gewünschten Bereich sehen kannst.
Bestimme dann über
 in den Grenzen des Intervalls
in den Grenzen des Intervalls ![\(\left[3,4\right]\)](https://mathjax.schullv.de/7734fc0dd6c6e75ca34b98f59ecc7339f9e4d0a62ff6c5404bfa99b3b4f32923?color=5a5a5a) .
.
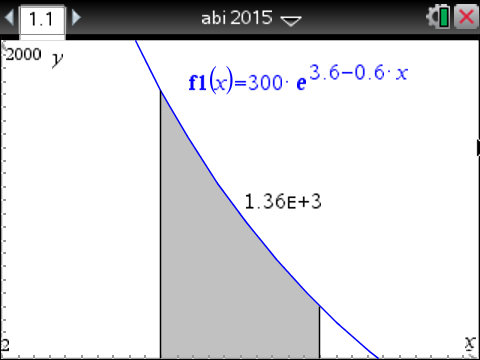 Der Anstieg im Laufe des vierten Tages ist also ca. 1.360 Pantoffeltierchen.
(5)
Der Anstieg im Laufe des vierten Tages ist also ca. 1.360 Pantoffeltierchen.
(5)
 Funktionsgleichung
Funktionsgleichung  für
für  bestimmen
Hier sollst du eine Funktionsgleichung
bestimmen
Hier sollst du eine Funktionsgleichung  aufstellen, welche die Anzahl der Pantoffeltierchen nach dem dritten Tag beschreibt. Du hast hierzu
aufstellen, welche die Anzahl der Pantoffeltierchen nach dem dritten Tag beschreibt. Du hast hierzu  und
und  gegeben. Die Funktion muss nun folgende Form haben:
gegeben. Die Funktion muss nun folgende Form haben:
![\(\begin{array}[t]{rll}
N_2(t)&=& \left( \text{Anzahl der Tierchen am dritten Tag}\right) \\[5pt]
&&\scriptsize{+ \left( \text{Anzahl der Tierchen, die ab dem dritten Tag bis zum Zeitpunkt } t \text{ dazugekommen sind}\right)}
\end{array}\)](https://mathjax.schullv.de/cdcda7d63eafa11f0d9a34b5ffcdd5d0eef49a25c1caa30ebed5376c90eccdd7?color=5a5a5a) 1. Schritt: Anzahl der Tierchen am dritten Tag bestimmen
Die Anzahl der Tierchen am dritten Tag hast du bereits mit
1. Schritt: Anzahl der Tierchen am dritten Tag bestimmen
Die Anzahl der Tierchen am dritten Tag hast du bereits mit  in Teilaufgabe a) berechnet.
in Teilaufgabe a) berechnet.
Diese lautet: .
2. Schritt: Anzahl der Tierchen nach dem dritten Tag bestimmen
Die Anzahl der Tierchen, die ab dem dritten Tag bis zum Zeitpunkt
.
2. Schritt: Anzahl der Tierchen nach dem dritten Tag bestimmen
Die Anzahl der Tierchen, die ab dem dritten Tag bis zum Zeitpunkt  dazukommen, kannst du nun mit Hilfe der Änderungsrate
dazukommen, kannst du nun mit Hilfe der Änderungsrate  bestimmen. Diese Anzahl ist gerade das Integral über
bestimmen. Diese Anzahl ist gerade das Integral über  von 3 bis
von 3 bis  :
:
![\(\begin{array}[t]{rll}
\displaystyle\int_{3}^{t} r_2(x) \;\mathrm dx &= \displaystyle\int_{3}^{t} 300 \cdot \mathrm e^{3,6 - 0,6 \cdot x} \;\mathrm dx \\[5pt]
&= 300 \cdot \displaystyle\int_{3}^{t} f(x) \;\mathrm dx & \quad \mid\; \scriptsize{F \small{\text{ Stammfunktion von }} f} \\[5pt]
&= 300 \cdot \left(F\left(t\right) - F\left(3\right) \right) \\[5pt]
&= 300 \cdot \left( \left(-\dfrac{5}{3}\right) \cdot \mathrm e^{3,6 - 0,6 \cdot t} - \left(-\dfrac{5}{3}\right) \cdot \mathrm e^{3,6 - 0,6 \cdot 3}\right) \\[5pt]
&= 300 \cdot \left(\dfrac{5}{3} \cdot \mathrm e^{1,8} - \dfrac{5}{3} \cdot \mathrm e^{3,6 - 0,6 \cdot t}\right) \\[5pt]
&= 500 \cdot \mathrm e^{1,8} - 500 \cdot \mathrm e^{3,6 - 0,6 \cdot t}
\end{array}\)](https://mathjax.schullv.de/865f18df47a68b6ea536019c82bcbabbbc97bf4547669ccd8e715aac2610921e?color=5a5a5a) 3. Schritt: Funktionsgleichung
3. Schritt: Funktionsgleichung  aufstellen
Setze nun die Ergebnisse aus dem ersten und zweiten Schritt in die obige Gleichung ein:
aufstellen
Setze nun die Ergebnisse aus dem ersten und zweiten Schritt in die obige Gleichung ein:
![\(\begin{array}[t]{rll}
N_2(t)&= N_1(3) + \displaystyle\int_{3}^{t} r_2(x) \;\mathrm dx \\[5pt]
&= \left(500 \cdot \mathrm e^{1,8}\right) + \left(500 \cdot \mathrm e^{1,8} - 500 \cdot \mathrm e^{3,6 - 0,6 \cdot t}\right) \\[5pt]
&= 1.000 \cdot \mathrm e^{1,8} - 500 \cdot \mathrm e^{3,6 - 0,6 \cdot t}
\end{array}\)](https://mathjax.schullv.de/11c2276b962c66f278984e069e6e5fd246428bb2863843ec33e2ecb888956e6d?color=5a5a5a) (6)
(6)
 Begründen, dass die Anzahl der Pantoffeltierchen nicht größer als
Begründen, dass die Anzahl der Pantoffeltierchen nicht größer als  wird
Um zu begründen, dass die Anzahl der Tierchen nicht größer als 6.050 wird, benötigst du eine Eigenschaft der Exponentialfunktion. Für alle
wird
Um zu begründen, dass die Anzahl der Tierchen nicht größer als 6.050 wird, benötigst du eine Eigenschaft der Exponentialfunktion. Für alle  gilt:
gilt:  , somit gilt auch
, somit gilt auch  für alle
für alle  . Damit gilt auch die Gleichung
. Damit gilt auch die Gleichung  . Also kannst du die Funktionsgleichung folgendermaßen abschätzen:
. Also kannst du die Funktionsgleichung folgendermaßen abschätzen:
 Damit hast du gezeigt, dass die Anzahl der Pantoffeltierchen zu keinem Zeitpunkt größer als
Damit hast du gezeigt, dass die Anzahl der Pantoffeltierchen zu keinem Zeitpunkt größer als  wird.
wird.
6: Graph analysieren  6:Integral
6:Integral  Untere Schranke 3
Untere Schranke 3  Obere Schranke 4
Obere Schranke 4
das Integral über 
Diese lautet:
a) (1)
 Funktionswert berechnen und Interpretation im Sachzusammenhang
Deine Aufgabe ist es hier, den Funktionswert von
Funktionswert berechnen und Interpretation im Sachzusammenhang
Deine Aufgabe ist es hier, den Funktionswert von  an der Stelle
an der Stelle  zu berechnen. Setze dazu
zu berechnen. Setze dazu  in die Funktionsgleichung
in die Funktionsgleichung  ein:
ein:
 Nun ist noch danach gefragt, den Funktionswert zu interpretieren.
Nun ist noch danach gefragt, den Funktionswert zu interpretieren.  wird als Anzahl der Pantoffeltierchen zum Zeitpunkt
wird als Anzahl der Pantoffeltierchen zum Zeitpunkt  aufgefasst, wobei
aufgefasst, wobei  als Maßzahl zur Einheit
als Maßzahl zur Einheit  Tag aufgefasst wird. Somit beschreibt
Tag aufgefasst wird. Somit beschreibt  die Anzahl der Pantoffeltierchen nach
die Anzahl der Pantoffeltierchen nach  Tagen.
(2)
Tagen.
(2)
 Zeitpunkt, zu dem
Zeitpunkt, zu dem  Pantoffeltierchen vorhanden sind, berechnen
Hier ist nach dem Zeitpunkt gefragt, zu dem
Pantoffeltierchen vorhanden sind, berechnen
Hier ist nach dem Zeitpunkt gefragt, zu dem  Pantoffeltierchen in der Nährlösung vorhanden sind. Also ist nach dem
Pantoffeltierchen in der Nährlösung vorhanden sind. Also ist nach dem  gesucht, für das
gesucht, für das  gilt. Setze dazu den Funktionsterm mit
gilt. Setze dazu den Funktionsterm mit  gleich und löse nach
gleich und löse nach  auf:
auf:
![\(\begin{array}[t]{rll}
N_1(t)&=2.000 & \quad \\[5pt]
500 \cdot \mathrm e^{0,6 \cdot t}&=2.000 & \quad \mid\; :500 \\[5pt]
\mathrm e^{0,6 \cdot t}&=4 & \quad \mid\; \ln \\[5pt]
0,6 \cdot t &= \ln(4) &\quad \mid\; :0,6 \\[5pt]
t&=\dfrac{\ln(4)}{0,6} \\[5pt]
&\approx 2,31
\end{array}\)](https://mathjax.schullv.de/5634c6e48e8c9c1921e5086d65df7c7a96274ca92709b33526b0414fc283626f?color=5a5a5a) Also sind nach ca.
Also sind nach ca.  Tagen
Tagen  Pantoffeltierchen in der Nährlösung vorhanden.
(3)
Pantoffeltierchen in der Nährlösung vorhanden.
(3)
 Durchschnittliches Wachstum der Anzahl der Pantoffeltierchen
Das durchschnittliche Wachstum an den ersten drei Tagen berechnest du, indem du die Anzahl an neu dazugekommenen Pantoffeltierchen durch die Anzahl an vergangenen Tagen teilst. Die Anzahl der neu dazugekommenen Pantoffeltierchen ist die Differenz von Pantoffeltierchen zu Beginn und der Pantoffeltierchen nach 3 Tagen, also
Durchschnittliches Wachstum der Anzahl der Pantoffeltierchen
Das durchschnittliche Wachstum an den ersten drei Tagen berechnest du, indem du die Anzahl an neu dazugekommenen Pantoffeltierchen durch die Anzahl an vergangenen Tagen teilst. Die Anzahl der neu dazugekommenen Pantoffeltierchen ist die Differenz von Pantoffeltierchen zu Beginn und der Pantoffeltierchen nach 3 Tagen, also  . Damit erhältst du:
. Damit erhältst du:
 Das durchschnittliche Wachstum der Pantoffeltierchen an den ersten drei Tagen beträgt
Das durchschnittliche Wachstum der Pantoffeltierchen an den ersten drei Tagen beträgt  Tierchen pro Tag.
(4)
Tierchen pro Tag.
(4)
 Begründen, warum die Funktion nur für einen begrenzten Zeitraum geeignet ist
Eine Funktion mit dem Funktionsterm
Begründen, warum die Funktion nur für einen begrenzten Zeitraum geeignet ist
Eine Funktion mit dem Funktionsterm  beschreibt exponentielles Wachstum. Der Grenzwert einer solchen Funktion ist "
beschreibt exponentielles Wachstum. Der Grenzwert einer solchen Funktion ist " ". Nach einem begrenzten Zeitraum wird die Anzahl der Pantoffeltierchen wegen des beschränkten Platz- und Nahrungsangebot in der Nährlösung jedoch nicht weiter unbeschränkt wachsen. Das unbeschränkte Wachstum steht somit im Widerspruch zu dem beschränkten Platz- und Nahrungsangebot. Damit ist eine solche Funktion nur für einen begrenzten Zeitraum für das Experiment geeignet.
". Nach einem begrenzten Zeitraum wird die Anzahl der Pantoffeltierchen wegen des beschränkten Platz- und Nahrungsangebot in der Nährlösung jedoch nicht weiter unbeschränkt wachsen. Das unbeschränkte Wachstum steht somit im Widerspruch zu dem beschränkten Platz- und Nahrungsangebot. Damit ist eine solche Funktion nur für einen begrenzten Zeitraum für das Experiment geeignet.
b)
 Interpretation im Sachzusammenhang
Der erste Teil der Aussage lautet
Interpretation im Sachzusammenhang
Der erste Teil der Aussage lautet  . Dies bedeutet, dass die momentane Änderungsrate zu jedem Zeitpunkt echt größer 0 ist. Also steigt die Anzahl der Tierchen immer weiter an.
Der zweite Teil der Aussage lautet
. Dies bedeutet, dass die momentane Änderungsrate zu jedem Zeitpunkt echt größer 0 ist. Also steigt die Anzahl der Tierchen immer weiter an.
Der zweite Teil der Aussage lautet  . Die Ableitung von
. Die Ableitung von  , also
, also  , beschreibt die Änderungsrate von
, beschreibt die Änderungsrate von  . Diese ist positiv, daher nimmt
. Diese ist positiv, daher nimmt  mit der Zeit größer werdende Werte an. Dies bedeutet im Sachzusammenhang, dass der Anstieg der Anzahl der Tierchen immer größer wird.
Insgesamt lässt sich sagen, dass die Anzahl der Pantoffeltierchen zu jeder Zeit steigt und dieser Anstieg immer größer wird.
mit der Zeit größer werdende Werte an. Dies bedeutet im Sachzusammenhang, dass der Anstieg der Anzahl der Tierchen immer größer wird.
Insgesamt lässt sich sagen, dass die Anzahl der Pantoffeltierchen zu jeder Zeit steigt und dieser Anstieg immer größer wird.
c) (1)
 Gleichheit zeigen
Berechne jeweils die beiden Funktionswerte, um die Gleichheit zu zeigen. Setze dazu
Gleichheit zeigen
Berechne jeweils die beiden Funktionswerte, um die Gleichheit zu zeigen. Setze dazu  in die Funktionsgleichung von
in die Funktionsgleichung von  ein bzw.
ein bzw.  in die Funktionsgleichung von
in die Funktionsgleichung von  ein:
ein:

 Damit ist gezeigt, dass für alle
Damit ist gezeigt, dass für alle  die Gleichung gilt.
(2)
die Gleichung gilt.
(2)
 Interpretation im Sachzusammenhang
Die Gleichung
Interpretation im Sachzusammenhang
Die Gleichung  bedeutet, dass die Änderungsraten der Anzahl der Pantoffeltierchen zu den Zeitpunkten
bedeutet, dass die Änderungsraten der Anzahl der Pantoffeltierchen zu den Zeitpunkten  und
und  gleich sind. Diese beiden Zeitpunkte sind "gleich weit" vom Zeitpunkt
gleich sind. Diese beiden Zeitpunkte sind "gleich weit" vom Zeitpunkt  entfernt. Beispielsweise bedeutet dies, dass die Änderunsrate am zweiten Tag gleich der Änderungsrate am vierten Tag ist (hier ist also
entfernt. Beispielsweise bedeutet dies, dass die Änderunsrate am zweiten Tag gleich der Änderungsrate am vierten Tag ist (hier ist also  ). Also kann man sagen, dass die Änderungsraten symmetrisch um den dritten Tag verteilt sind.
(3)
). Also kann man sagen, dass die Änderungsraten symmetrisch um den dritten Tag verteilt sind.
(3)
 Zeige, dass
Zeige, dass  Stammfunktion von
Stammfunktion von  ist
ist
 ist eine Stammfunktion von
ist eine Stammfunktion von  , wenn die Ableitung von
, wenn die Ableitung von  gerade
gerade  ist, also
ist, also  gilt. Leite dazu
gilt. Leite dazu  ab, beachte dabei die Kettenregel zu verwenden:
ab, beachte dabei die Kettenregel zu verwenden:
![\(\begin{array}[t]{rll}
F(x)&=&-\dfrac{5}{3} \cdot \mathrm e^{3,6 - 0,6 \cdot t} & \quad \scriptsize \\[10pt]
F‘(x)&=&\left(-\dfrac{5}{3}\right) \cdot \mathrm e^{3,6 - 0,6 \cdot x} \cdot \left(-0,6\right)\\[5pt]
&=&\mathrm e^{3,6 - 0,6 \cdot x}\\[5pt]
&=&f(x)
\end{array}\)](https://mathjax.schullv.de/5f73e4768f3bcd666b276b1ab4c3ee061adb4ff60af0b42a4afc56471e814b90?color=5a5a5a) Damit hast du gezeigt, dass
Damit hast du gezeigt, dass  eine Stammfunktion von
eine Stammfunktion von  ist.
(4)
ist.
(4)
 Anstieg im Laufe des vierten Tages berechnen
Hier sollst du den Anstieg der Anzahl der Pantoffeltierchen im Laufe des vierten Tages berechnen. Diesen kannst du mit der momentanen Änderungsrate bestimmen. Die momentane Änderungsrate beschreibt hier das Wachstum der Pantoffeltierchen, damit beschreibt das Integral über die Änderungsrate innerhalb eines Zeitintervalls den insgesamten Anstieg der Pantoffeltierchen innerhalb dieses Zeitraums.
Die Anzahl an Pantoffeltierchen, die im Laufe des Tages hinzugekommen sind, ist hier also gerade das Integral über die momentane Änderungsrate
Anstieg im Laufe des vierten Tages berechnen
Hier sollst du den Anstieg der Anzahl der Pantoffeltierchen im Laufe des vierten Tages berechnen. Diesen kannst du mit der momentanen Änderungsrate bestimmen. Die momentane Änderungsrate beschreibt hier das Wachstum der Pantoffeltierchen, damit beschreibt das Integral über die Änderungsrate innerhalb eines Zeitintervalls den insgesamten Anstieg der Pantoffeltierchen innerhalb dieses Zeitraums.
Die Anzahl an Pantoffeltierchen, die im Laufe des Tages hinzugekommen sind, ist hier also gerade das Integral über die momentane Änderungsrate  von den Zeitpunkten
von den Zeitpunkten  bis
bis  . Somit beschreibt das Integral
. Somit beschreibt das Integral  die Anzahl an Tierchen, die im Laufe des vierten Tages dazugekommen sind. Dieses kannst du direkt per Hand oder mit deinem GTR berechnen:
die Anzahl an Tierchen, die im Laufe des vierten Tages dazugekommen sind. Dieses kannst du direkt per Hand oder mit deinem GTR berechnen:
 Lösungsweg A: Lösen per Hand
Lösungsweg A: Lösen per Hand
 In Aufgabenteil (3) hast du bereits gezeigt, dass
In Aufgabenteil (3) hast du bereits gezeigt, dass  eine Stammfunktion von
eine Stammfunktion von  ist. Somit kannst du hier den Hauptsatz der Integralrechnung anwenden:
ist. Somit kannst du hier den Hauptsatz der Integralrechnung anwenden:
![\(\begin{array}[t]{rll}
300 \cdot \displaystyle\int_{3}^{4} f(t)\; \mathrm dt &= 300 \cdot \left(F(4) - F(3)\right) \\[5pt]
&= 300 \cdot \left( \left(-\dfrac{5}{3}\right) \cdot \mathrm e^{3,6 - 0,6 \cdot 4} - \left(-\dfrac{5}{3}\right) \cdot \mathrm e^{3,6 - 0,6 \cdot 3}\right) \\[5pt]
&= 300 \cdot \left( \dfrac{5}{3} \cdot \mathrm e^{1,8} -\dfrac{5}{3} \cdot \mathrm e^{1,2} \right) \\[5pt]
&= 300 \cdot \dfrac{5}{3} \cdot \left( \mathrm e^{1,8} - \mathrm e^{1,2}\right)\\[5pt]
&= 500 \cdot \left( \mathrm e^{1,8} - \mathrm e^{1,2}\right) \\[5pt]
&\approx 1.364,77
\end{array}\)](https://mathjax.schullv.de/13ee43ef88b166ec036cc1276f0b6c910247528bfc2e1177099e6745f6261132?color=5a5a5a) Der Anstieg im Laufe des vierten Tages ist also ca.
Der Anstieg im Laufe des vierten Tages ist also ca.  Pantoffeltierchen.
Pantoffeltierchen.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über DRAW anzeigen.
Bestimme dann über
. Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über DRAW anzeigen.
Bestimme dann über
 in den Grenzen des Intervalls
in den Grenzen des Intervalls ![\(\left[3,4\right]\)](https://mathjax.schullv.de/7734fc0dd6c6e75ca34b98f59ecc7339f9e4d0a62ff6c5404bfa99b3b4f32923?color=5a5a5a) .
.
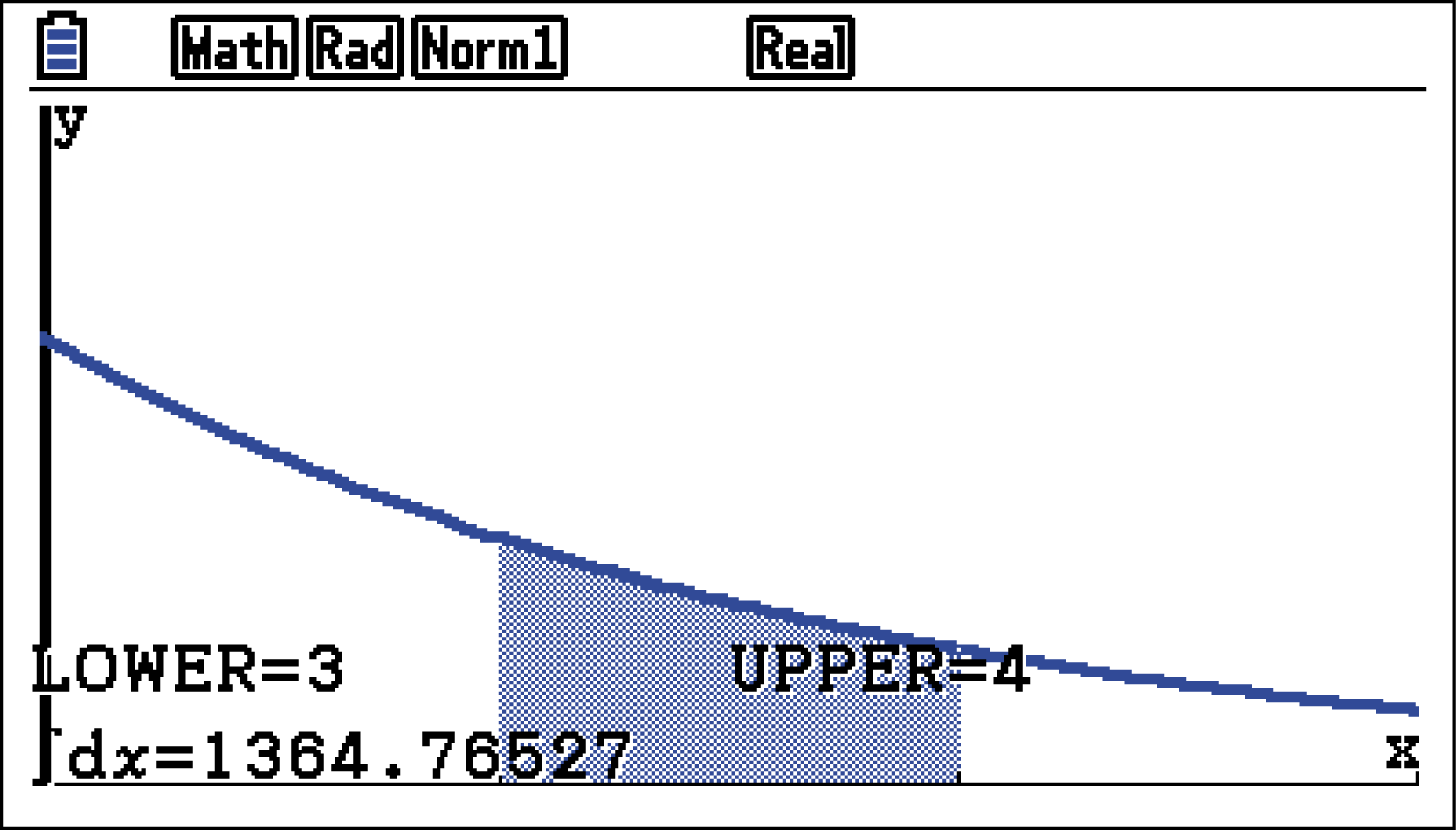 Der Anstieg im Laufe des vierten Tages ist also ca.
Der Anstieg im Laufe des vierten Tages ist also ca.  Pantoffeltierchen.
(5)
Pantoffeltierchen.
(5)
 Funktionsgleichung
Funktionsgleichung  für
für  bestimmen
Hier sollst du eine Funktionsgleichung
bestimmen
Hier sollst du eine Funktionsgleichung  aufstellen, welche die Anzahl der Pantoffeltierchen nach dem dritten Tag beschreibt. Du hast hierzu
aufstellen, welche die Anzahl der Pantoffeltierchen nach dem dritten Tag beschreibt. Du hast hierzu  und
und  gegeben. Die Funktion muss nun folgende Form haben:
gegeben. Die Funktion muss nun folgende Form haben:
![\(\begin{array}[t]{rll}
N_2(t)&=& \left( \text{Anzahl der Tierchen am dritten Tag}\right) \\[5pt]
&&\scriptsize{+ \left( \text{Anzahl der Tierchen, die ab dem dritten Tag bis zum Zeitpunkt } t \text{ dazugekommen sind}\right)}
\end{array}\)](https://mathjax.schullv.de/cdcda7d63eafa11f0d9a34b5ffcdd5d0eef49a25c1caa30ebed5376c90eccdd7?color=5a5a5a) 1. Schritt: Anzahl der Tierchen am dritten Tag bestimmen
Die Anzahl der Tierchen am dritten Tag hast du bereits mit
1. Schritt: Anzahl der Tierchen am dritten Tag bestimmen
Die Anzahl der Tierchen am dritten Tag hast du bereits mit  in Teilaufgabe a) berechnet.
in Teilaufgabe a) berechnet.
Diese lautet: .
2. Schritt: Anzahl der Tierchen nach dem dritten Tag bestimmen
Die Anzahl der Tierchen, die ab dem dritten Tag bis zum Zeitpunkt
.
2. Schritt: Anzahl der Tierchen nach dem dritten Tag bestimmen
Die Anzahl der Tierchen, die ab dem dritten Tag bis zum Zeitpunkt  dazukommen, kannst du nun mit Hilfe der Änderungsrate
dazukommen, kannst du nun mit Hilfe der Änderungsrate  bestimmen. Diese Anzahl ist gerade das Integral über
bestimmen. Diese Anzahl ist gerade das Integral über  von 3 bis
von 3 bis  :
:
![\(\begin{array}[t]{rll}
\displaystyle\int_{3}^{t} r_2(x) \;\mathrm dx &= \displaystyle\int_{3}^{t} 300 \cdot \mathrm e^{3,6 - 0,6 \cdot x} \;\mathrm dx \\[5pt]
&= 300 \cdot \displaystyle\int_{3}^{t} f(x) \;\mathrm dx & \quad \mid\;\scriptsize{F \small{\text{ Stammfunktion von }} f} \\[5pt]
&= 300 \cdot \left(F\left(t\right) - F\left(3\right) \right) \\[5pt]
&= 300 \cdot \left( \left(-\dfrac{5}{3}\right) \cdot \mathrm e^{3,6 - 0,6 \cdot t} - \left(-\dfrac{5}{3}\right) \cdot \mathrm e^{3,6 - 0,6 \cdot 3}\right) \\[5pt]
&= 300 \cdot \left(\dfrac{5}{3} \cdot \mathrm e^{1,8} - \dfrac{5}{3} \cdot \mathrm e^{3,6 - 0,6 \cdot t}\right) \\[5pt]
&= 500 \cdot \mathrm e^{1,8} - 500 \cdot \mathrm e^{3,6 - 0,6 \cdot t}
\end{array}\)](https://mathjax.schullv.de/c86fbd0a6ebc599ed90b8a92dfb01cac035c3efd031ed56bcac2398ee25163cd?color=5a5a5a) 3. Schritt: Funktionsgleichung
3. Schritt: Funktionsgleichung  aufstellen
Setze nun die Ergebnisse aus dem ersten und zweiten Schritt in die obige Gleichung ein:
aufstellen
Setze nun die Ergebnisse aus dem ersten und zweiten Schritt in die obige Gleichung ein:
![\(\begin{array}[t]{rll}
N_2(t)&= N_1(3) + \displaystyle\int_{3}^{t} r_2(x) \;\mathrm dx \\[5pt]
&= \left(500 \cdot \mathrm e^{1,8}\right) + \left(500 \cdot \mathrm e^{1,8} - 500 \cdot \mathrm e^{3,6 - 0,6 \cdot t}\right) \\[5pt]
&= 1.000 \cdot \mathrm e^{1,8} - 500 \cdot \mathrm e^{3,6 - 0,6 \cdot t}
\end{array}\)](https://mathjax.schullv.de/11c2276b962c66f278984e069e6e5fd246428bb2863843ec33e2ecb888956e6d?color=5a5a5a) (6)
(6)
 Begründen, dass die Anzahl der Pantoffeltierchen nicht größer als
Begründen, dass die Anzahl der Pantoffeltierchen nicht größer als  wird
Um zu begründen, dass die Anzahl der Tierchen nicht größer als 6.050 wird, benötigst du eine Eigenschaft der Exponentialfunktion. Für alle
wird
Um zu begründen, dass die Anzahl der Tierchen nicht größer als 6.050 wird, benötigst du eine Eigenschaft der Exponentialfunktion. Für alle  gilt:
gilt:  , somit gilt auch
, somit gilt auch  für alle
für alle  . Damit gilt auch die Gleichung
. Damit gilt auch die Gleichung  . Also kannst du die Funktionsgleichung folgendermaßen abschätzen:
. Also kannst du die Funktionsgleichung folgendermaßen abschätzen:
 Damit hast du gezeigt, dass die Anzahl der Pantoffeltierchen zu keinem Zeitpunkt größer als
Damit hast du gezeigt, dass die Anzahl der Pantoffeltierchen zu keinem Zeitpunkt größer als  wird.
wird.
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F6
F6  F3 (
F3 ( dx)
dx)  F1 (
F1 ( dx)
dx)
das Integral über 
Diese lautet: