Aufgabe 2

Für jede reelle Zahl $k \gt 0$ ist durch die Gleichung

$f_k(x) = x^3-k\cdot x,$ $x\in \mathbb{R},$

eine Funktion $f_k$ gegeben.

(1)

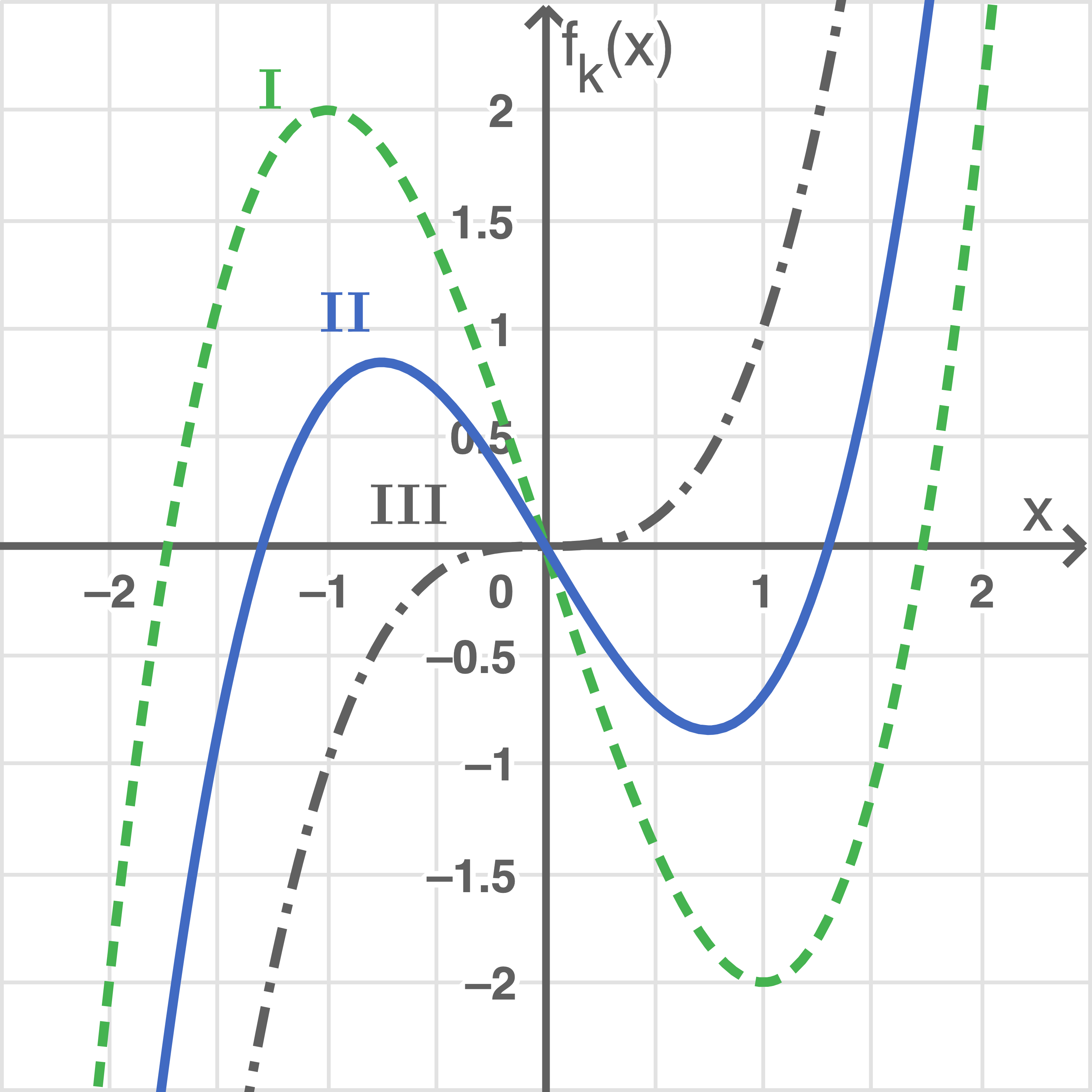
Die in der nebenstehenden Abbildung 1 dargestellten Graphen $\text{I},$ $\text{II}$ und $\text{III}$ gehören jeweils zu einem der Werte $k = 1 ,$ $k = 2$ und $k = 3.$

Entscheide, welcher Wert zu welchem Graphen gehört.

(2)

Ermittle denjenigen Wert von $k,$ für den der Punkt $(0,5\mid -1)$ auf dem Graphen von $f_k$ liegt.

Abbildung 1

(3 + 3 Punkte)

Im Folgenden wird die konkrete Funktion $f_1$ mit der Gleichung

$f_1(x)=x^3-x,$ $x\in \mathbb{R},$

betrachtet.

Untersuche die Funktion $f_1$ rechnerisch auf lokale Extremstellen.

(7 Punkte)

(1)

Bestimme rechnerisch den Inhalt der Fläche, die für $x \leq 0$ vom Graphen von $f_1$ und der $x$ -Achse eingeschlossen wird.

(2)

In der folgenden Abbildung 2 siehst du den Graphen von $f_1$ und eine Gerade $g_a:\, y= a\cdot x,$ die den Graphen von $f_1$ an drei Stellen $x=s_1,$ $x=0$ und $x=s_3$ schneidet.

Abbildung 2

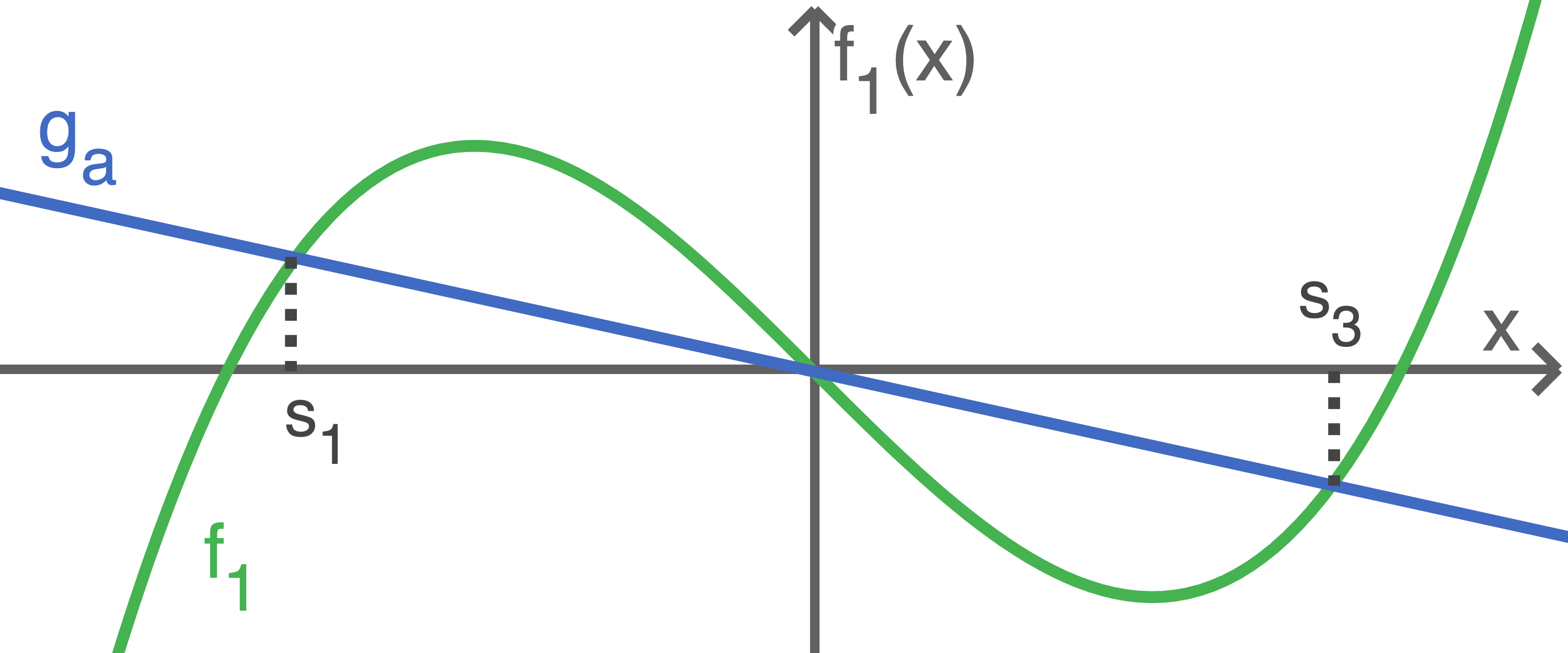Gib für die in Abbildung 2 dargestellte Situation ohne weitere Berechnung den Wert des Integrals $\displaystyle\int_{s_1}^{s_3}(f_1(x)-a\cdot x)\;\mathrm dx$ an.
Begründe deine Angabe.

(6 + 5 Punkte)

(1)

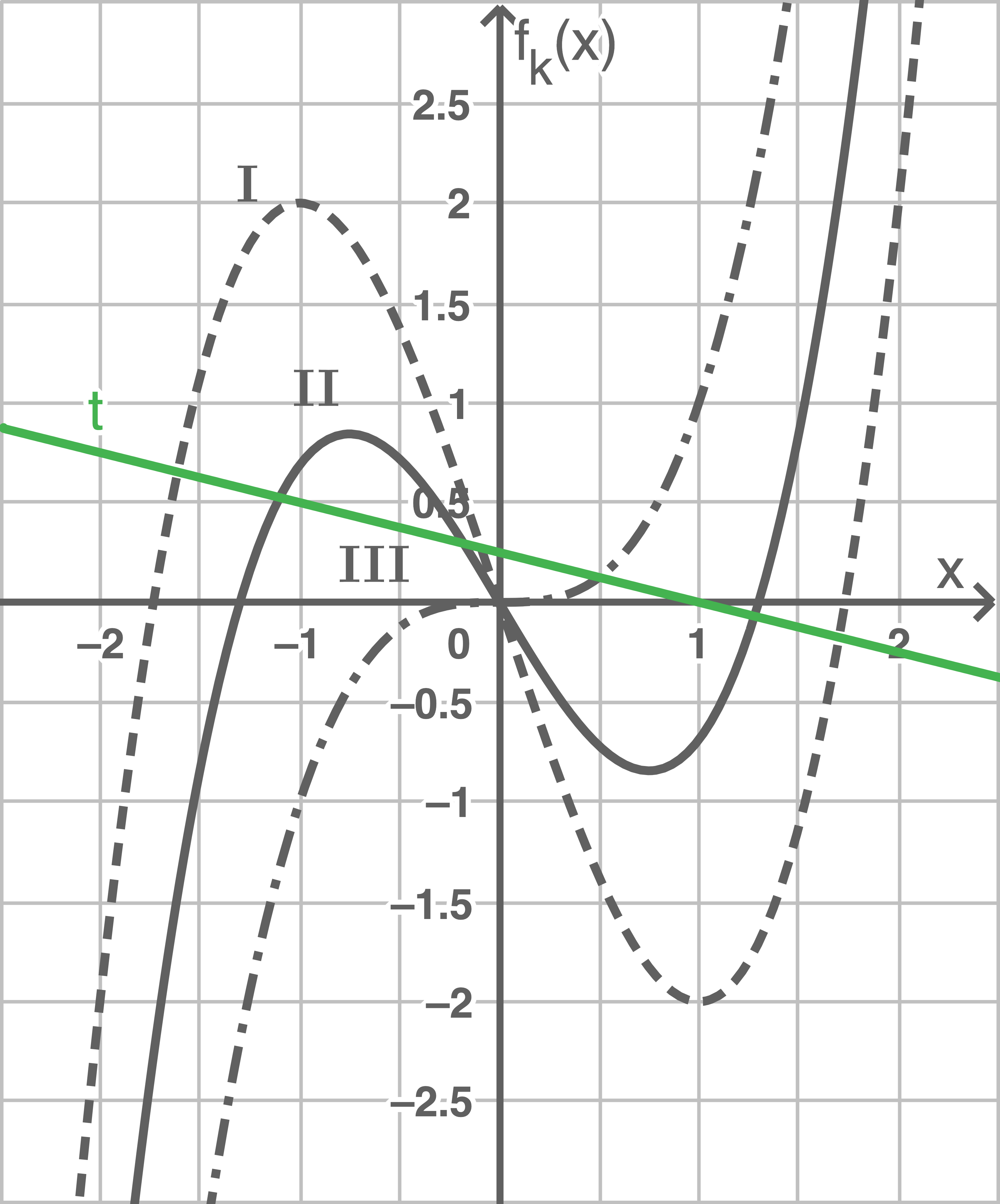
Zeichne die Gerade $t:\, y= -0,25\cdot x +0,25$ in die Abbildung 3 ein.

(2)

Weise rechnerisch nach, dass $t$ eine Tangente an den Graphen von $f_1$ ist.

(3)

Die Tangente $t$ und der Graph von $f_1$ schließen eine Fläche ein.
Ermittle den Inhalt dieser Fläche.

(4)

Zeige: Für jede reelle Zahl $r\gt 0$ ist die Gerade durch die Punkte $A_r\left(-r\mid f_1(-r) \right)$ und $B_r\left(2\cdot r\mid f_1(2\cdot r)\right)$ eine Tangente an den Graphen von $f_1$ im Punkt $A_r.$

Abbildung 3

(2+5+4+5 Punkte)

(1)

$\blacktriangleright$ Parameterwerte und Graphen zuordnen

Je größer der Wert von $k,$ desto extremer werden auch die Extrema von $f_k.$

$k=1$ gehört zu Graph $\text{III}$

$k=2$ gehört zu Graph $\text{II}$

$k=3$ gehört zu Graph $\text{I}$

(2)

$\blacktriangleright$ Parameterwert ermitteln

$k=2,25$

Vollständige Lösung anzeigen

Für $k=2,25$ liegt der Punkt $(0,5\mid -1)$ auf dem Graphen von $f_k.$

$\blacktriangleright$ Funktion auf lokale Extremstellen untersuchen

1. Schritt: Ableitungsfunktionen bestimmen

$\begin{array}[t]{rll} f_1(x) &=& x^3 -x\\[5pt] f_1‘(x) &=& 3x^2 -1 \\[5pt] f_1‘‘(x) &=& 6x \end{array}$

2. Schritt: Notwendiges Kriterium für lokale Extremstellen anwenden

$\begin{array}[t]{rll} f_1‘(x) &=& 0 \\[5pt] 3x^2 -1 &=& 0 &\quad \scriptsize \mid\; +1 \\[5pt] 3x^2 &=& 1 &\quad \scriptsize \mid\; :3 \\[5pt] x^2 &=& \frac{1}{3} \\[5pt] x_1&=& -\frac{1}{\sqrt{3}} \\[5pt] x_2 &=& \frac{1}{\sqrt{3}} \end{array}$

3. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen

$\begin{array}[t]{rll} f_1‘‘\left(-\frac{1}{\sqrt{3}} \right)&=& 6\cdot \left( -\frac{1}{\sqrt{3}}\right) \lt 0 \\[5pt] f_1‘‘\left(\frac{1}{\sqrt{3}} \right)&=& 6\cdot \frac{1}{\sqrt{3}} \gt 0 \\[5pt] \end{array}$

$f_1$ besitzt an der Stelle $x_1=-\frac{1}{\sqrt{3}}$ ein lokales Maximum und an der Stelle $x_2 = \frac{1}{\sqrt{3}}$ ein lokales Minimum.

(1)

$\blacktriangleright$ Flächeninhalt bestimmen

1. Schritt: Integrationsgrenzen bestimmen

Die Integrationsgrenzen entsprechen den Nullstellen von $f_1$ für $x\leq 0.$

$\begin{array}[t]{rll} f_1(x) &=& 0 \\[5pt] x_1 &=& 0 \\[5pt] x_2 &=& -1 \\[5pt] x_3 &=& 1 \end{array}$

Vollständige Lösung anzeigen

2. Schritt: Flächeninhalt berechnen

$A=0,25$

Vollständige Lösung anzeigen

Der Inhalt der Fläche, die der Graph von $f_1$ für $x\leq 0$ mit der $x$ -Achse einschließt, beträgt $0,25\,\text{FE}.$

(2)

$\blacktriangleright$ Wert ohne Berechnung angeben und begründen

$\displaystyle\int_{s_1}^{s_3}(f_1(x)-a\cdot x)\;\mathrm dx = 0$

In den Funktionstermen von $f_1$ und $g_a$ kommen nur ungerade Exponenten vor. Die zugehörigen Graphen sind daher punktsymmetrisch zum Koordinatenursprung.
Es ist daher $s_3 = -s_1.$
Mit dem oben angegebenen Integral wird die Flächenbilanz aller Inhalte der Flächen gebildet, die der Graph von $f_1$ und $g_a$ im Intervall $[s_1;s_3]$ einschließen.
Es handelt sich dabei um zwei Flächen, die im betrachteten Intervall von den beiden Graphen eingeschlossen werden, eine im Intervall $[s_1;0]$ und eine im Intervall $[0;s_3].$

Wegen der Punktsymmetrie beider Graphen besitzen beide Flächen den gleichen Flächeninhalt.
Im Intervall $[s_1;0]$ ist allerdings $f_1$ die obere Randfunktion, im Intervall $[0;s_3]$ ist $g_a$ die obere Randfunktion. Da das Integral über $(f_1(x)-g_a(x))$ gebildet wird, geht die Fläche im Intervall $[s_1;0]$ negativ in die Flächenbilanz ein und die Fläche im Intervall $[0;s_3]$ positiv. Dadurch heben sich die beiden Flächeninhalt gegenseitig auf, weshalb der Wert des Interals Null ist.

(1)

$\blacktriangleright$ Gerade einzeichnen

(2)

$\blacktriangleright$ Tangente nachweisen

1. Schritt: Stelle mit der Tangentensteigung bestimmen

$\begin{array}[t]{rll} f_1‘(x) &=& -0,25 \\[5pt] x_1 &=& 0,5 \\[5pt] x_2 &=& -0,5 \end{array}$

Vollständige Lösung anzeigen

2. Schritt: Koordinaten überprüfen

$\begin{array}[t]{rll} f_1(-0,5) &=& \frac{3}{8} \\[10pt] t(-0,5) &=& \frac{3}{8} \\[10pt] \end{array}$

Vollständige Lösung anzeigen

An der Stelle $x=-0,5$ besitzen $f_1$ und $t$ sowohl die gleiche Steigung als auch den gleichen Funktionswert. $t$ ist also eine Tangente an den Graphen von $f_1$ an der Stelle $x=-0,5.$

(3)

$\blacktriangleright$ Flächeninhalt ermitteln

1. Schritt: Integrationsgrenzen bestimmen

Bestimme die Schnittstellen von $f_1$ und $t$ mit deinem GTR, indem du beide Graphen anzeigen lässt und die Schnittstellen bestimmen lässt.

$\begin{array}[t]{rll} f_1(x) &=& t(x) \\[5pt] x_1&=& -0,5\\[5pt] x_2&=& 1 \end{array}$

Vollständige Lösung anzeigen

2. Schritt: Flächeninhalt bestimmen

Lass dir den Graphen von $t(x)-f_1(x)$ in deinem GTR anzeigen und bestimme den Wert des Integrals im Intervall $[-0,5;1].$

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 7: $\int f(x)\;\mathrm dx$

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F3: $\int \;\mathrm dx$

$A \approx 0,42$

Vollständige Lösung anzeigen

Der Inhalt der von den beiden Graphen von $f_1$ und $t$ eingeschlossenen Fläche beträgt ca. $0,42\,\text{FE}.$

(4)

$\blacktriangleright$ Tangente zeigen

1. Schritt: Steigung der Gerade durch $A_{r}$ und $B_{r}$ bestimmen

$m_{A;B}=3r^2-1$

Vollständige Lösung anzeigen

2. Schritt: Steigung der Tangente an der Stelle $x=-r$ bestimmen

$\begin{array}[t]{rll} f_1‘(-r)&=& 3\cdot (-r)^2 -1 \\[5pt] &=& 3r^2-1 \end{array}$

Die Steigung der Geraden durch die Punkte $A_{r}$ und $B_{r}$ stimmt mit der Steigung der Tangente an den Graphen von $f_1$ an der Stelle $x=-r$ überein. Zudem verlaufen beide Geraden durch den Punkt $(-r\mid f_1(-r))$ und sind damit identisch. Die Gerade durch die Punkte $A_{r}$ und $B_{r}$ ist also eine Tangente an den Graphen von $f_1$ im Punkt $A_r.$

Bildnachweise [nach oben]

[1]