Aufgabe 2
Die Abbildung zeigt den Graphen der in  definierten Funktion
definierten Funktion  mit
mit
 .
.
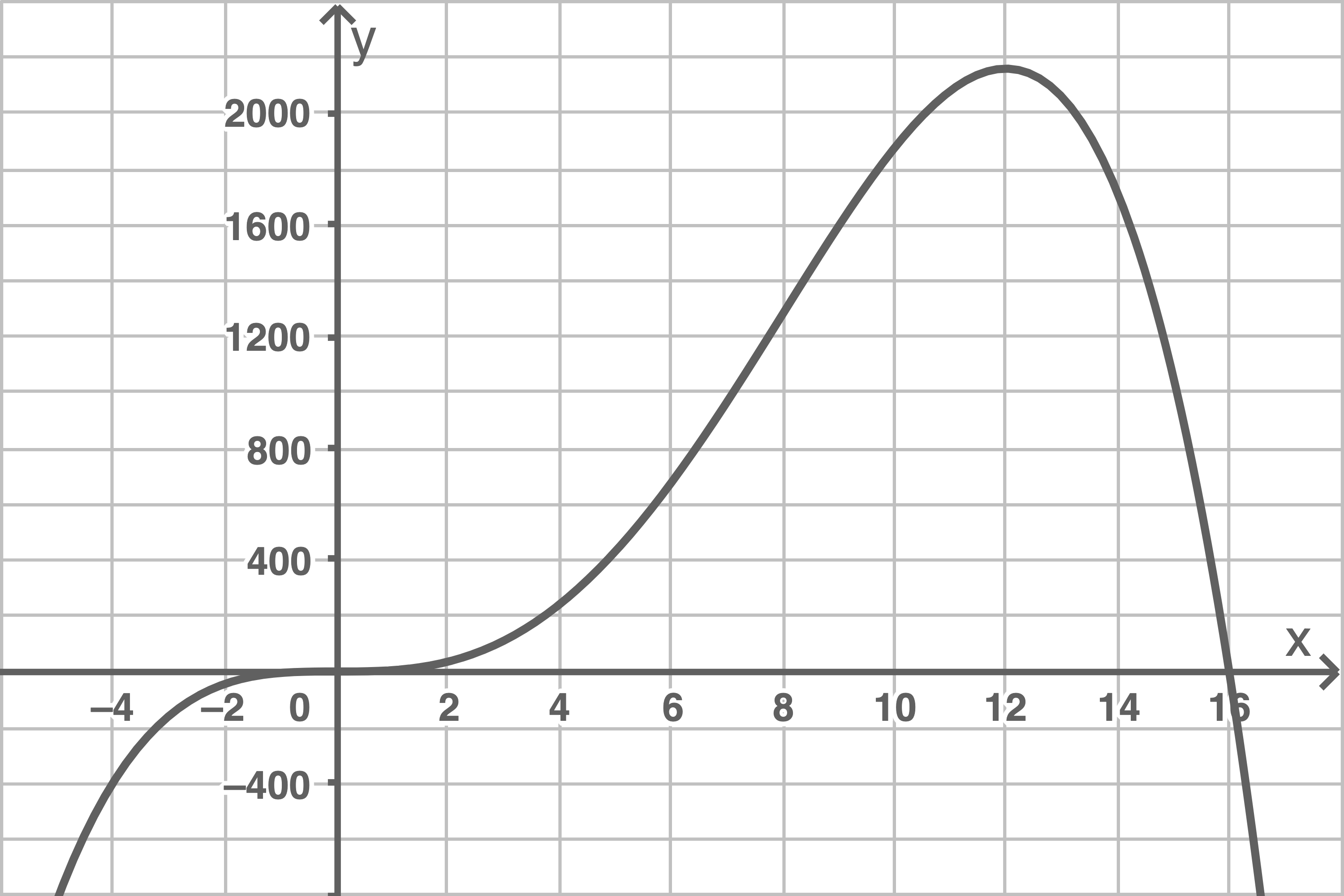

Abbildung
a)
(1)
Zeige rechnerisch, dass der Punkt  ein Hochpunkt des Graphen von
ein Hochpunkt des Graphen von  ist und dass die Tangente an den Graphen von
ist und dass die Tangente an den Graphen von  im Punkt
im Punkt  parallel zur
parallel zur  -Achse verläuft.
-Achse verläuft.
(2)
Bestimme eine Gleichung der Geraden  die durch die beiden Wendepunkte des Graphen von
die durch die beiden Wendepunkte des Graphen von  verläuft.
verläuft.
Zeichne in die Abbildung eine Gerade ein, die parallel zu ist und für
ist und für  mit dem Graphen von
mit dem Graphen von  genau einen Punkt gemeinsam hat.
genau einen Punkt gemeinsam hat.
Zeichne in die Abbildung eine Gerade ein, die parallel zu
(3)
Die Punkte  ,
,  und
und  bilden für jede reelle Zahl
bilden für jede reelle Zahl  mit
mit  ein Dreieck
ein Dreieck  Ermittle denjenigen Wert von
Ermittle denjenigen Wert von  für den der Flächeninhalt des Dreiecks
für den der Flächeninhalt des Dreiecks  maximal wird, und gib diesen Flächeninhalt an.
[Hinweis: Eine Betrachtung der Randwerte ist nicht erforderlich.]
maximal wird, und gib diesen Flächeninhalt an.
[Hinweis: Eine Betrachtung der Randwerte ist nicht erforderlich.]
(5 + 6 + 4 Punkte)
b)
Für jede reelle Zahl  ist eine in
ist eine in  definierte Funktion
definierte Funktion  mit
mit  gegeben.
gegeben.
(1)
Beschreibe, wie der Graph von  aus dem Graphen von
aus dem Graphen von  erzeugt werden kann.
erzeugt werden kann.
(2)
Bestimme denjenigen Wert von  für den der Punkt
für den der Punkt  auf dem Graphen von
auf dem Graphen von  liegt.
liegt.
(3)
Die Gleichung  hat genau die drei Lösungen
hat genau die drei Lösungen  ,
,  und
und  und es gilt
und es gilt  .
Erläutere die geometrische Bedeutung dieser Aussage in Bezug auf die Graphen von
.
Erläutere die geometrische Bedeutung dieser Aussage in Bezug auf die Graphen von  und
und  .
.
(4)
Ermittle, an welchen Stellen im Intervall ![\([0;16]\)](https://mathjax.schullv.de/cca3dbd8ff2a1c2c095f5bf7a33edd60fac28cb4474c29ad127c2eb06ca63447?color=5a5a5a) die Graphen der Funktionen
die Graphen der Funktionen  und
und  einen vertikalen Abstand von
einen vertikalen Abstand von  Längeneinheiten haben.
Längeneinheiten haben.
(2 + 2 + 3 + 4 Punkte)
c)
Ein Unternehmen lagert Glyzerin in einem Tank. Die momentane Änderungsrate des Tankinhalts kann für  mithilfe der Funktion
mithilfe der Funktion  (aus a)) beschrieben werden. Dabei ist
(aus a)) beschrieben werden. Dabei ist  die seit Beobachtungsbeginn vergangene Zeit in Stunden und
die seit Beobachtungsbeginn vergangene Zeit in Stunden und  die momentane Änderungsrate in Kilogramm pro Stunde. Zu Beobachtungsbeginn befinden sich im Tank
die momentane Änderungsrate in Kilogramm pro Stunde. Zu Beobachtungsbeginn befinden sich im Tank  Glyzerin.
Glyzerin.
(1)
Der Punkt  liegt auf dem Graphen von
liegt auf dem Graphen von  .
Interpretiere die Koordinaten dieses Punktes im Sachzusammenhang.
.
Interpretiere die Koordinaten dieses Punktes im Sachzusammenhang.
(2)
Beurteile die folgende Aussage: "Zwölf Stunden nach Beobachtungsbeginn ist die größte Menge Glyzerin im Tank enthalten."
(3)
Bestimme die Zunahme des Tankinhalts zwischen den Zeitpunkten acht Stunden und zehn Stunden nach Beobachtungsbeginn.
(4)
Berechne, wie viel Glyzerin  Stunden nach Beobachtungsbeginn im Tank enthalten ist.
Stunden nach Beobachtungsbeginn im Tank enthalten ist.
(2 + 2 + 2 + 3 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
1. Schritt: Die ersten beiden Ableitungen bilden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/c190baf86bbefd35789647c55e788b46e5cd5a721ce216e571c84032b3388ac2?color=5a5a5a)
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/0f178b73e350f32f59633ee25bc618e925e88d3e0e5ebfec9d9a68ec9486efef?color=5a5a5a) 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/9726556335b9fa5759f6ce1be6838a3a1b55ff9fe9f65887f2bc046fece90145?color=5a5a5a) Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  oder
oder  und daraus:
und daraus:
![\(\begin{array}[t]{rll}
-\dfrac{5}{4} \cdot x +15&=& 0 &\quad \scriptsize \mid\;+\dfrac{5}{4} \cdot x \\[5pt]
15&=& \dfrac{5}{4} \cdot x &\quad \scriptsize \mid\; :\dfrac{5}{4} \\[5pt]
12&=& x_2 \\[5pt]
x_2&=& 12
\end{array}\)](https://mathjax.schullv.de/6ef29631904ee9c80231bf346a158d5a24b4275df311e46a0e2381a6211c8c9a?color=5a5a5a) 3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
 Da
Da 
 und
und  hat der Graph von
hat der Graph von  einen Hochpunkt in
einen Hochpunkt in  .
Es gilt
.
Es gilt  Deshalb verläuft die Tangente an den Graphen von
Deshalb verläuft die Tangente an den Graphen von  im Punkt
im Punkt  parallel zur
parallel zur  -Achse.
-Achse.
(2)
1. Schritt: Wendepunkte bestimmen
Die Wendestellen entsprechen den Extremstellen von Diese werden mit dem Taschenrechner graphisch bestimmt.
Diese werden mit dem Taschenrechner graphisch bestimmt.
 TI 84-PLUS
TI 84-PLUS
 Casio fx-CG
Es ergeben sich zwei Extremstellen der Ableitung an
Casio fx-CG
Es ergeben sich zwei Extremstellen der Ableitung an  und
und  also zwei Wendepunkte des Graphen von
also zwei Wendepunkte des Graphen von  Diese haben die Koordinaten
Diese haben die Koordinaten  und
und  2. Schritt: Geradengleichung bestimmen
Die Gerade verläuft durch den Ursprung und durch den Punkt
2. Schritt: Geradengleichung bestimmen
Die Gerade verläuft durch den Ursprung und durch den Punkt  Für die Steigung der Geraden gilt
Für die Steigung der Geraden gilt 
Die Geradengleichung folgt mit 3. Schritt: Parallele Gerade einzeichnen
3. Schritt: Parallele Gerade einzeichnen
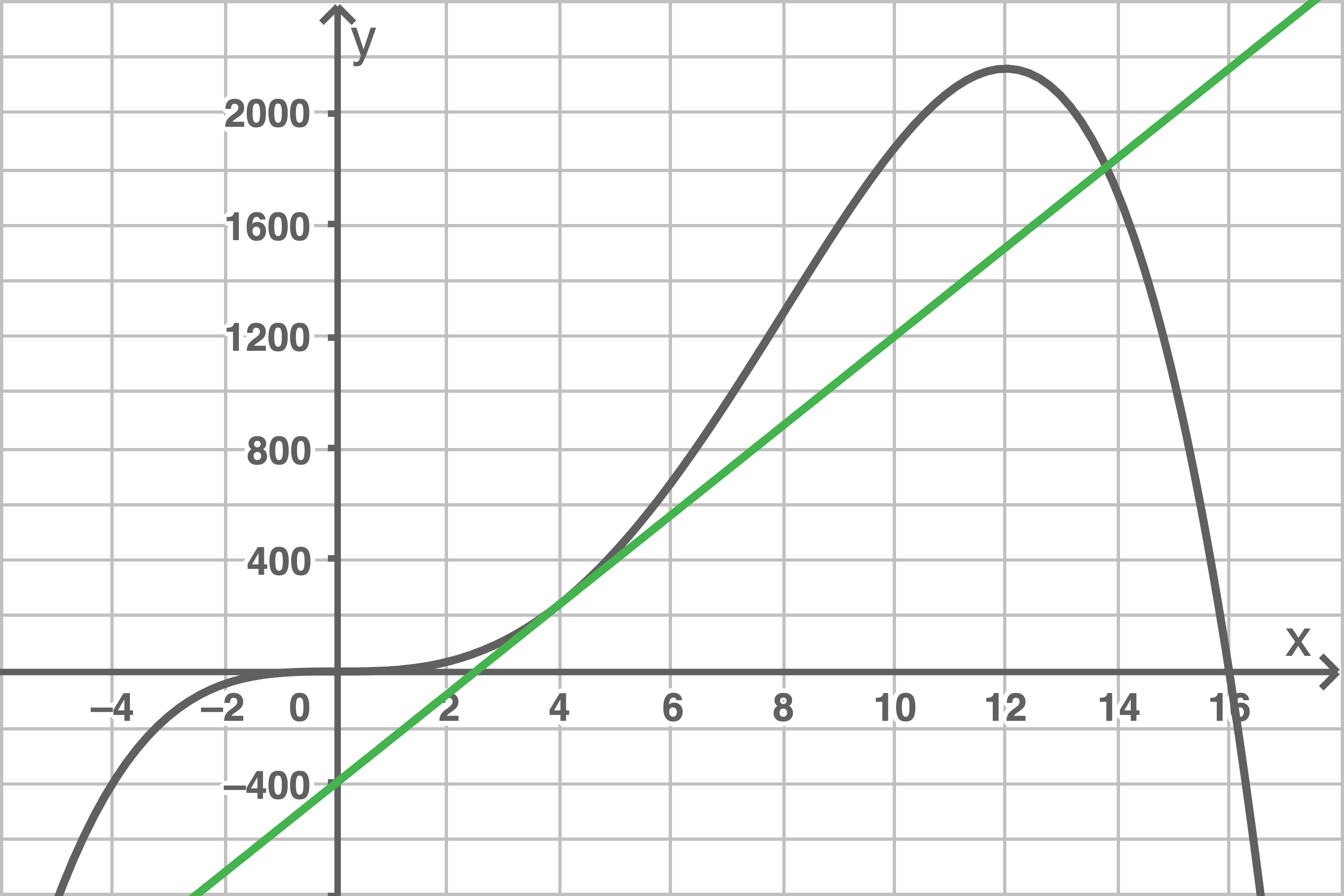
Die Wendestellen entsprechen den Extremstellen von
2nd  trace (calc)
trace (calc)  4: maximum
4: maximum
F5 (G-Solv)  F2: MAX
F2: MAX
Die Geradengleichung folgt mit

(3)
1. Schritt: Funktion zur Berechnung des Flächeninhalts aufstellen
Der Flächeninhalt eines Dreiecks wird allgemein mit  berechnet.
Im Dreieck
berechnet.
Im Dreieck  gilt:
gilt:  und
und  Daraus folgt:
Daraus folgt:
![\(\begin{array}[t]{rll}
A(b)&=& \dfrac{1}{2} \cdot b \cdot f(b) &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2} \cdot b\cdot \left(-\dfrac{5}{16} \cdot b^4 +5 \cdot b^3 \right) &\quad \scriptsize \\[5pt]
&=&-\dfrac{5}{32} \cdot b^5 +\dfrac{5}{2} \cdot b^4
\end{array}\)](https://mathjax.schullv.de/42be62ceadcf4cb774fae1a637e1535b4bd0c6951ee589109b6a8132532a2124?color=5a5a5a) 2. Schritt: Maximalwert bestimmen
Das Maximum des Flächeninhalts wird graphisch mit dem Taschenrechner ermittelt.
2. Schritt: Maximalwert bestimmen
Das Maximum des Flächeninhalts wird graphisch mit dem Taschenrechner ermittelt.
 TI 84-PLUS
TI 84-PLUS
 Casio fx-CG
Der Hochpunkt hat die Koordinaten
Casio fx-CG
Der Hochpunkt hat die Koordinaten  Somit nimmt der Flächeninhalt des Dreiecks für
Somit nimmt der Flächeninhalt des Dreiecks für  seinen Maximalwert mit
seinen Maximalwert mit  an.
an.
2nd  trace (calc)
trace (calc)  3: minimum
3: minimum
F5 (G-Solv)  F3: MIN
F3: MIN
b)
(1)
Der Graph von  entsteht, durch Streckung des Graphen von
entsteht, durch Streckung des Graphen von  in
in  -Richtung um den Faktor
-Richtung um den Faktor 
(2)
Es ist  Einsetzen der Koordinaten
Einsetzen der Koordinaten  in die Gleichung von
in die Gleichung von  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
h_a(4)&=& 240& \quad \scriptsize \\[5pt]
5a \cdot 4^2 &=& 240 & \quad \scriptsize \\[5pt]
80 \cdot a&=& 240\quad \scriptsize \mid :80\\[5pt]
a &=& 3
\end{array}\)](https://mathjax.schullv.de/15d7f15201a002fca69cae572fb6939c08948bfdbddefa72c652b3536c93ad1c?color=5a5a5a)
(3)
Die Graphen von  und
und  haben genau drei gemeinsame Punkte. Sie schließen zwei Flächenstücke ein. Da das Integral den Wert Null hat, haben die beiden Flächenstücke den gleichen Flächeninhalt. Ein Flächenstück liegt unter dem Graphen von
haben genau drei gemeinsame Punkte. Sie schließen zwei Flächenstücke ein. Da das Integral den Wert Null hat, haben die beiden Flächenstücke den gleichen Flächeninhalt. Ein Flächenstück liegt unter dem Graphen von  und über dem Graphen von
und über dem Graphen von  , das andere liegt über dem Graphen von
, das andere liegt über dem Graphen von  und unter dem Graphen von
und unter dem Graphen von 
(4)
Der vertikale Abstand der beiden Funktionsgraphen wird durch  beschrieben. Dieser Abstand soll
beschrieben. Dieser Abstand soll  betragen. Gesucht sind folglich die
betragen. Gesucht sind folglich die  - Werte für die
- Werte für die  bzw.
bzw.  gilt.
Es folgt
gilt.
Es folgt 
 Für
Für  ergeben sich mit dem solve-Befehl des Taschenrechners die Lösungen
ergeben sich mit dem solve-Befehl des Taschenrechners die Lösungen  und
und  Für
Für  ergeben sich mit dem solve-Befehl des Taschenrechners die Lösungen
ergeben sich mit dem solve-Befehl des Taschenrechners die Lösungen  und
und  Jedoch liegt
Jedoch liegt  nicht im betrachteten Intervall.
Die Funktionsgraphen haben einen vertikalen Abstand von
nicht im betrachteten Intervall.
Die Funktionsgraphen haben einen vertikalen Abstand von  für
für  und
und 
c)
(1)
Die Änderungsrate des Tankinhalts beträgt vier Stunden nach Beobachtungsbeginn  kg/h.
kg/h.
(2)
Die Aussage ist falsch. Die momentane Änderungsrate erreicht zwölf Stunden nach Beobachtungsbeginn ihr Maximum, ist aber danach noch vier Stunden positiv, weshalb die Menge Glyzerin im Tank weiter zunimmt.
(3)
Es gilt ![\(\displaystyle\int_{8}^{10}f(x)\;\mathrm dx =3178 \;[\text{kg}].\)](https://mathjax.schullv.de/518a89c8a2be63172fda63000e93c05ec9c8f15263982bb2450ac5a0322124bd?color=5a5a5a) Die Zunahme des Tankinhalts zwischen den Zeitpunkten acht Stunden und zehn Stunden nach Beobachtungsbeginn beträgt
Die Zunahme des Tankinhalts zwischen den Zeitpunkten acht Stunden und zehn Stunden nach Beobachtungsbeginn beträgt 
(4)