Aufgabe 5
Das Produkt „Fußball-Bundesliga“ ist ein Erfolgsmodell. Die Zuschauerzahlen erreichten in der Saison 2011/12 einen Rekord von durchschnittlich mehr als 40.000 pro Spiel. Dabei ist das Publikum mittlerweile zu  weiblich.
weiblich.
Dieser Prozentsatz soll im Folgenden als Wahrscheinlichkeit verwendet werden.
Dieser Prozentsatz soll im Folgenden als Wahrscheinlichkeit verwendet werden.
a) Berechnen Sie die Wahrscheinlichkeit, dass sich unter 200 bei einem Bundesliga-Spiel zufällig ausgewählten Zuschauern1
- genau 48 weibliche Zuschauer befinden,
- mindestens 35 und höchstens 60 weibliche Zuschauer befinden,
- eine Anzahl von weiblichen Zuschauern befindet, die um mindestens 10 von ihrem Erwartungswert abweicht.
(2P + 3P + 5P)
1 Der Begriff „Zuschauer“soll stets männliche und weibliche Zuschauer umfassen.
b) Beschreiben Sie im vorliegenden Sachzusammenhang ein Ereignis  , dessen Wahrscheinlichkeit mit dem Term
, dessen Wahrscheinlichkeit mit dem Term
 berechnet werden kann.
[Hinweis: Der Wert dieses Terms muss nicht berechnet werden.]
berechnet werden kann.
[Hinweis: Der Wert dieses Terms muss nicht berechnet werden.]
(4P)
c) Bei einem Bundesliga-Spiel strömen 20.000 Zuschauer ins Stadion. An weibliche Zuschauer soll ein Flyer verteilt werden, der auf ein spezielles Getränkeangebot hinweist.
- Ermitteln Sie auf der Grundlage der 20.000 Zuschauer das zum Erwartungswert symmetrische Intervall kleinster Länge, in dem die Anzahl der weiblichen Zuschauer mit einer Wahrscheinlichkeit von mindestens 0,9 liegt.
- Vor dem Spiel bildet sich an einem Kassenhäuschen eine Schlange von 50 Zuschauern. Nennen Sie eine Voraussetzung, unter der die Wahrscheinlichkeit P, dass sich in der Schlange 12 weibliche Zuschauer befinden, folgendermaßen berechnet werden kann:
Entscheiden Sie, ob diese Berechnung in der vorliegenden Situation zulässig ist.
(6P + 5P)
d) Im Deutschen Fußballbund (DFB) sind 1.077.215 weibliche Mitglieder gemeldet2, was einem Anteil von (ungefähr)  entspricht. Von diesen gehören
entspricht. Von diesen gehören  zur Alterklasse „Mädchen“, der Rest zur Altersklasse „Frauen“. Bei den männlichen Mitgliedern unterscheidet man die Altersklassen „Junioren“ und „Senioren“. Insgesamt beträgt der Anteil der Jugendlichen („Mädchen“ und „Junioren“) im DFB
zur Alterklasse „Mädchen“, der Rest zur Altersklasse „Frauen“. Bei den männlichen Mitgliedern unterscheidet man die Altersklassen „Junioren“ und „Senioren“. Insgesamt beträgt der Anteil der Jugendlichen („Mädchen“ und „Junioren“) im DFB  .
.
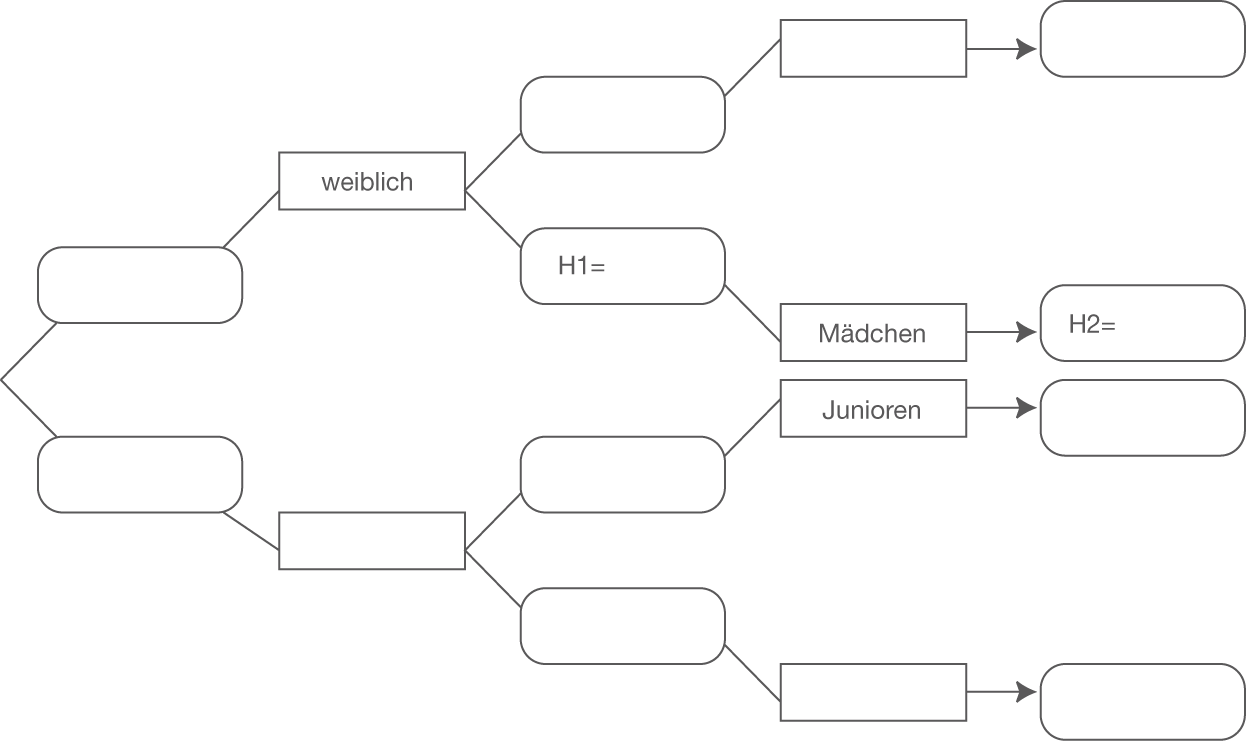
- Stellen Sie die gegebenen Daten in dem folgenden Baumdiagramm dar und notieren Sie alle fehlenden relativen Häufigkeiten.

- Beschreiben Sie die relativen Häufigkeiten, die im Diagramm als
bzw.
bezeichnet werden, mit Worten.
- Zwei Mitglieder des DFB werden zufällig ausgewählt.
Ermitteln Sie die Wahrscheinlichkeit, dass es sich bei den beiden Personen um einen männlichen Jugendlichen (Junior) und ein Mädchen handelt.
(7P + 3P +4P)
2 Gehen Sie davon aus, dass es sich um aktuelle Daten handelt.
e) Um den Stadionbesuch für weibliche Zuschauer attraktiver zu gestalten, werden für diese an Imbissständen des Stadions spezielle Angebote gemacht.
Der Verkaufsleiter vermutet, dass der Anteil weiblicher Zuschauer sogar auf über gestiegen ist, so dass er zusätzliche Vorräte für die speziellen Angebote bereitstellen müsste. Er möchte aber unbedingt vermeiden, auf größeren Mengen verderblicher Ware sitzen zu bleiben.
gestiegen ist, so dass er zusätzliche Vorräte für die speziellen Angebote bereitstellen müsste. Er möchte aber unbedingt vermeiden, auf größeren Mengen verderblicher Ware sitzen zu bleiben.
Um eine Entscheidung treffen zu können, nutzt er Fotos, die im Rahmen eines Anti-Hooligan-Programms von jedem einzelnen Zuschauer beim Einlass gemacht werden. Er lässt 1.000 zufällig auswählen und in dieser Stichprobe die Anzahl der Fotos bestimmen, die weibliche Zuschauer zeigen.
Der Verkaufsleiter vermutet, dass der Anteil weiblicher Zuschauer sogar auf über
Um eine Entscheidung treffen zu können, nutzt er Fotos, die im Rahmen eines Anti-Hooligan-Programms von jedem einzelnen Zuschauer beim Einlass gemacht werden. Er lässt 1.000 zufällig auswählen und in dieser Stichprobe die Anzahl der Fotos bestimmen, die weibliche Zuschauer zeigen.
- Der Verkaufsleiter testet die Nullhypothese
.
Begründen Sie die Wahl dieser Nullhypothese aus der Sicht des Verkaufsleiters und ermitteln Sie eine Entscheidungsregel für die genannte Stichprobe (Irrtumswahrscheinlichkeit 0,05). - Beschreiben Sie den Fehler 2.Art im Sachzusammenhang und berechnen Sie die Wahrscheinlichkeit seines Auftretens für den Fall, dass der Anteil der weiblichen Zuschauer tatsächlich
beträgt.
(7P + 4P)
Tabelle 1:  -Regeln für Binomialverteilungen
Eine mit den Parametern
-Regeln für Binomialverteilungen
Eine mit den Parametern  und
und  binomialverteilte Zufallsgröße
binomialverteilte Zufallsgröße  hat den Erwartungswert
hat den Erwartungswert  und die Standardabweichung
und die Standardabweichung  .
.
Wenn die LAPLACE-Bedingung erfüllt ist, gelten die
erfüllt ist, gelten die  -Regeln:
-Regeln:
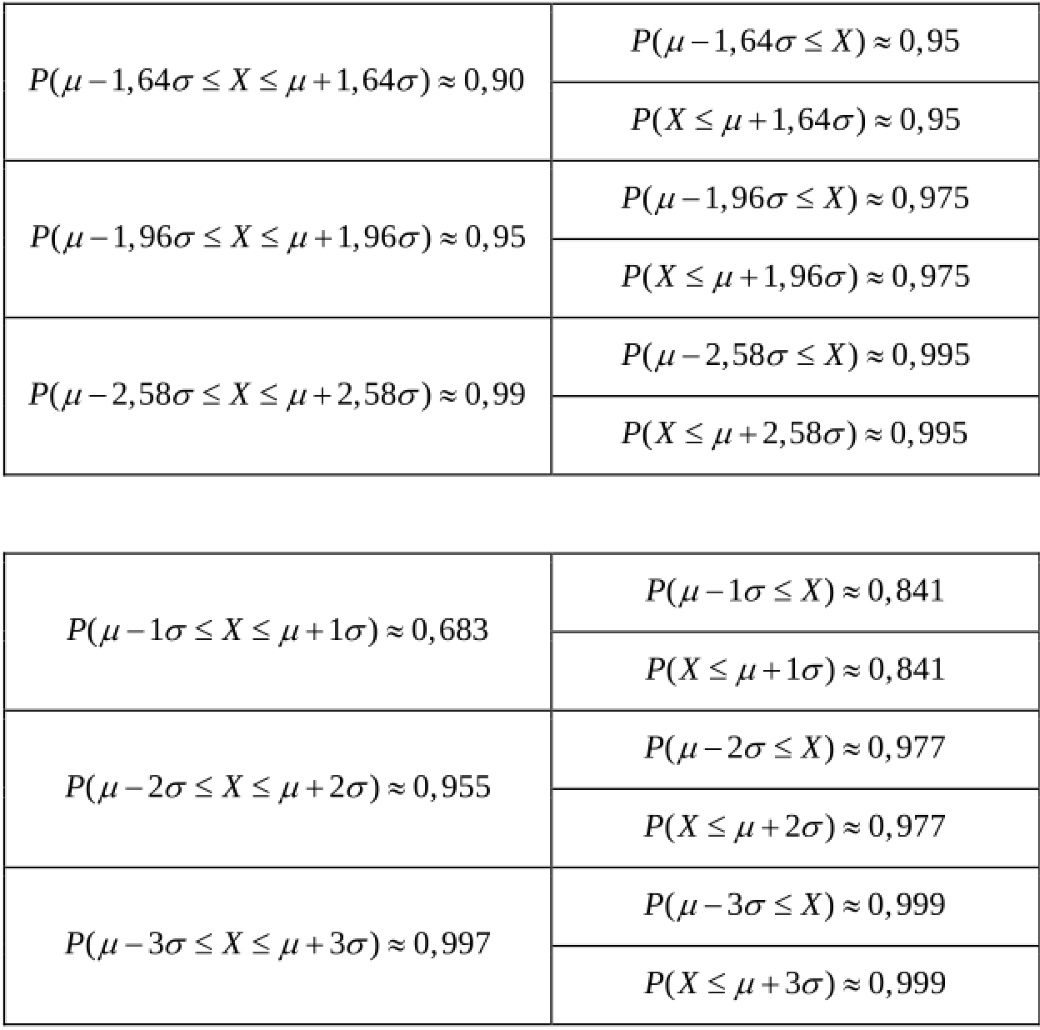 Tabelle 2: Kumulierte Binomialverteilung für n=10 und n=20
Tabelle 2: Kumulierte Binomialverteilung für n=10 und n=20

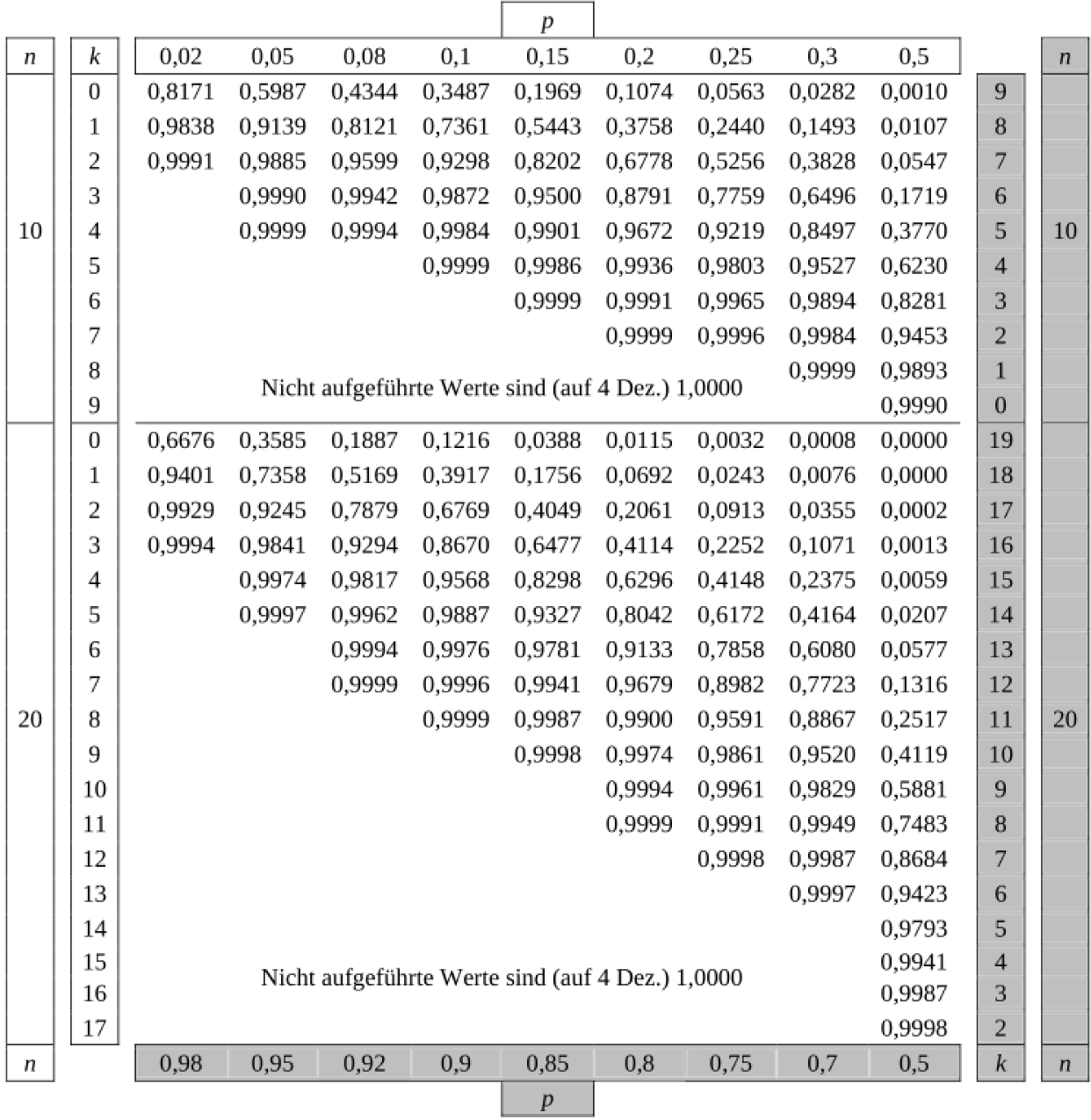 Bei grau unterlegtem Eingang, d.h.
Bei grau unterlegtem Eingang, d.h.  gilt:
gilt:  abgelesener Wert
Tabelle 3: Kumulierte Binomialverteilung für n=50
abgelesener Wert
Tabelle 3: Kumulierte Binomialverteilung für n=50

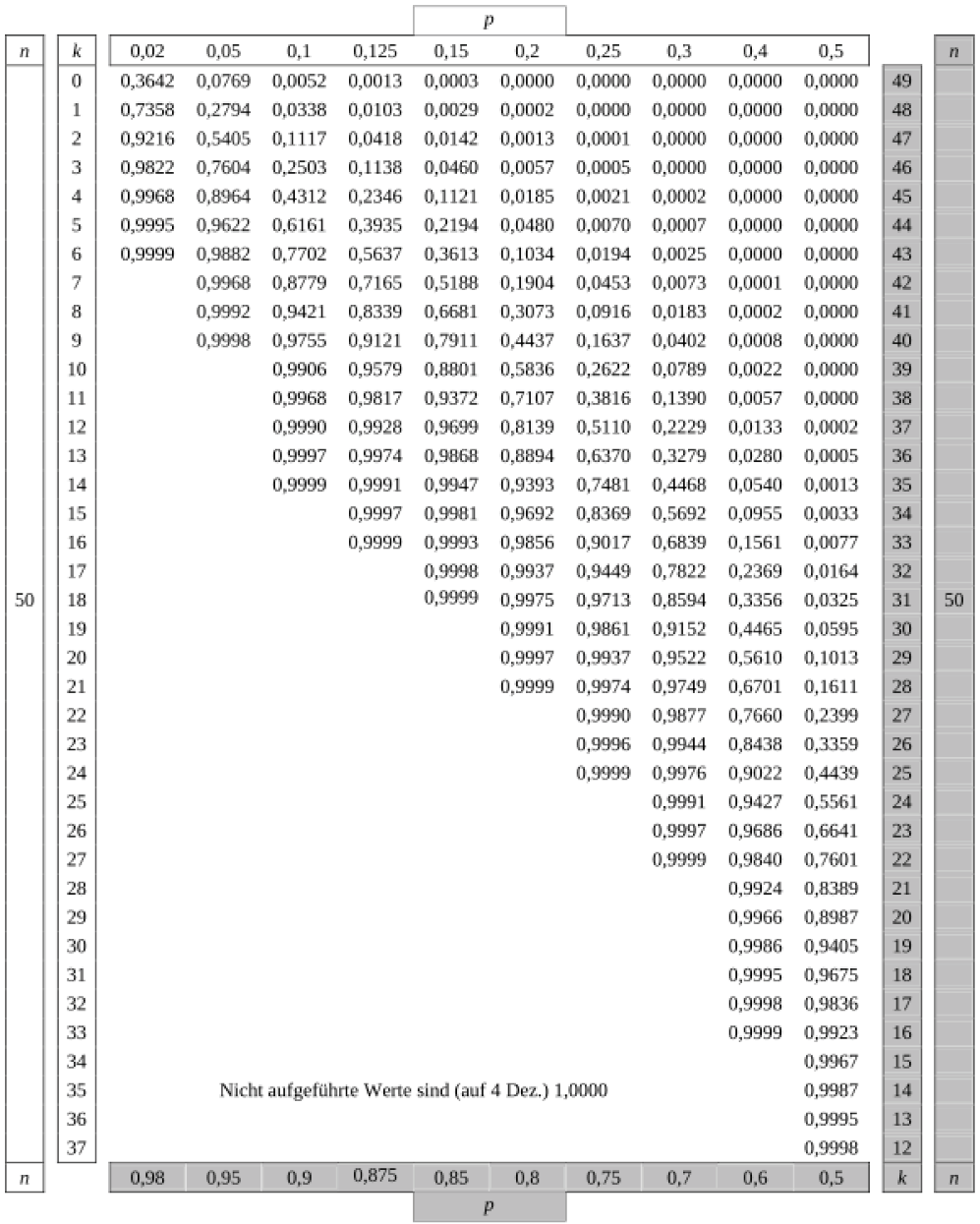 Bei grau unterlegtem Eingang, d.h.
Bei grau unterlegtem Eingang, d.h.  gilt:
gilt:  abgelesener Wert
Tabelle 4: Kumulierte Binomialverteilung für n=200
abgelesener Wert
Tabelle 4: Kumulierte Binomialverteilung für n=200

 Bei grau unterlegtem Eingang, d.h.
Bei grau unterlegtem Eingang, d.h.  gilt:
gilt:  abgelesener Wert
Tabelle 5: Kumulierte Binomialverteilung für n=1.000
abgelesener Wert
Tabelle 5: Kumulierte Binomialverteilung für n=1.000

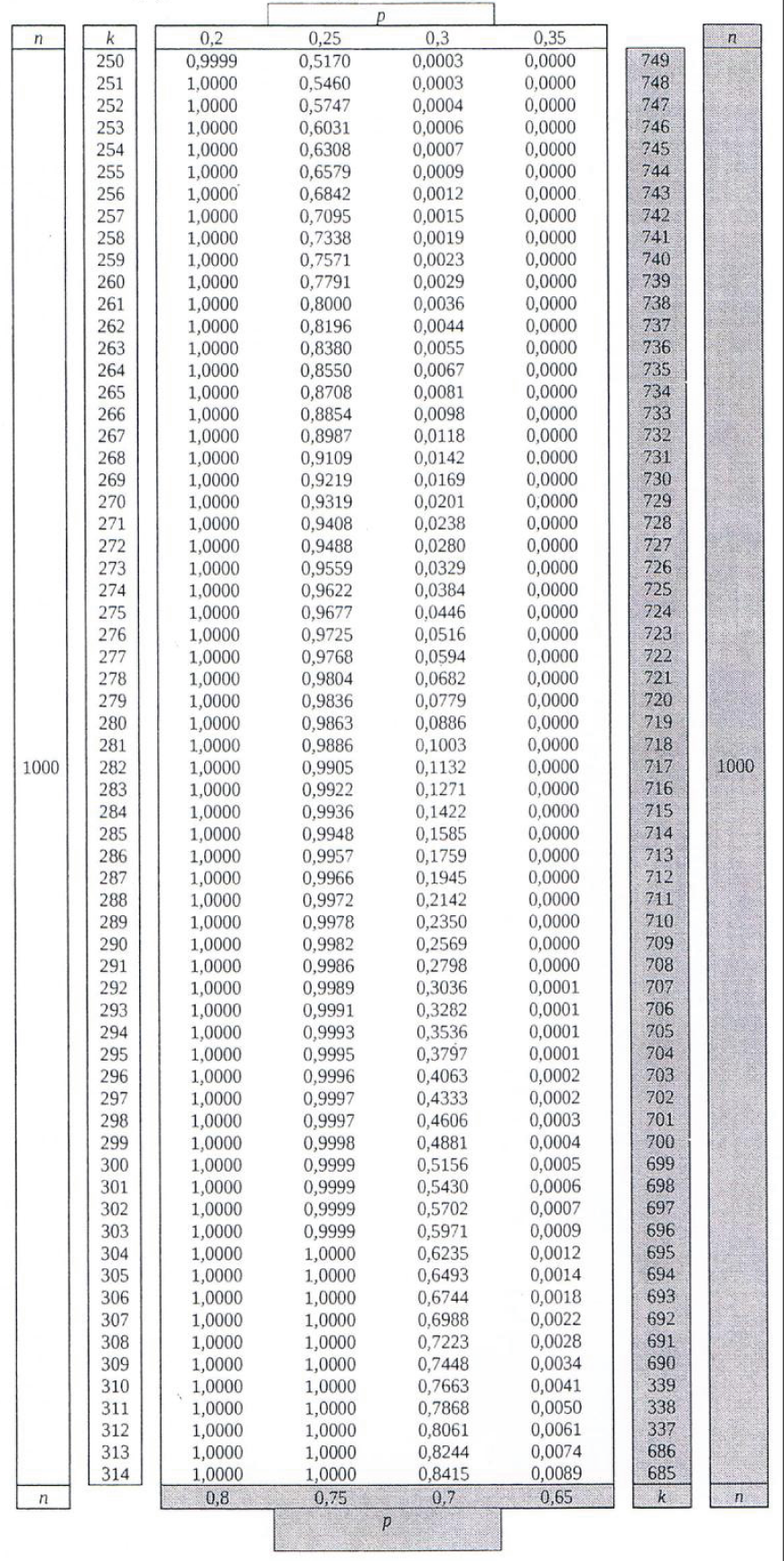 Bei grau unterlegtem Eingang, d.h.
Bei grau unterlegtem Eingang, d.h.  gilt:
gilt:  abgelesener Wert
Tabelle 6: Normalverteilung
abgelesener Wert
Tabelle 6: Normalverteilung


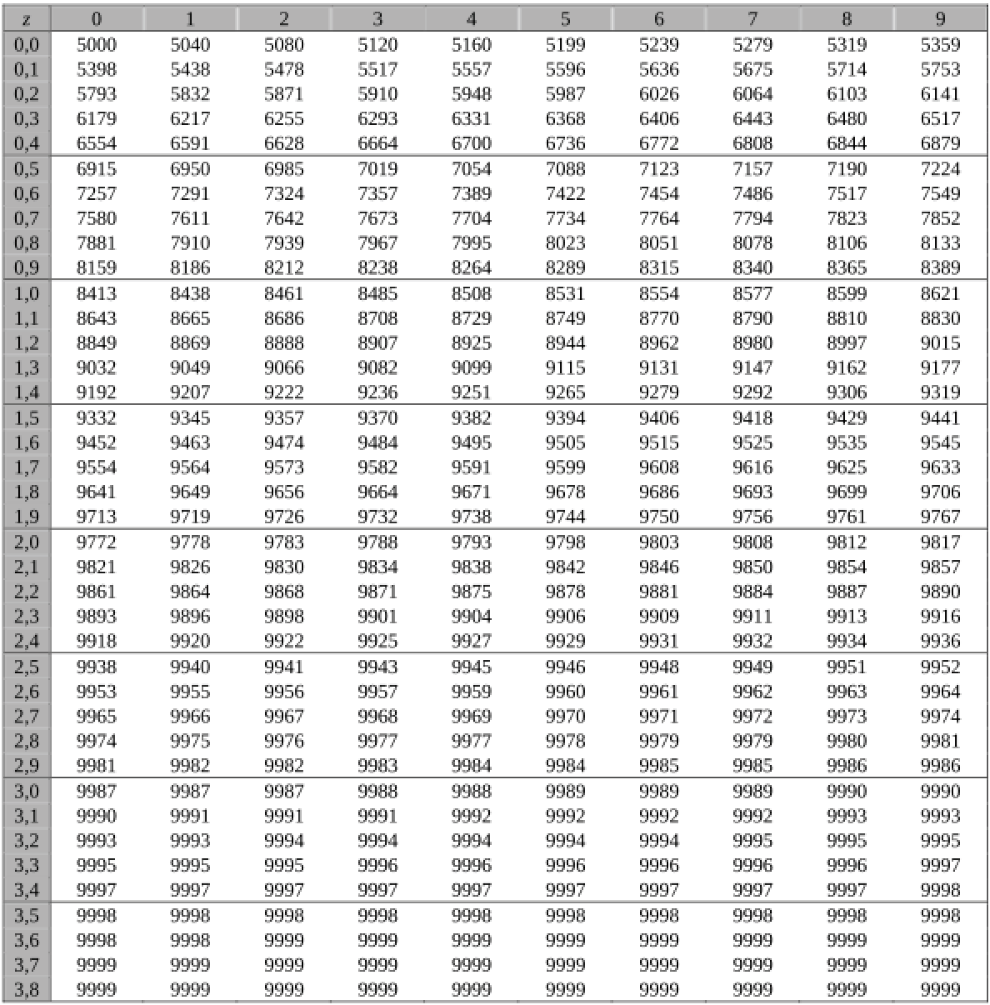 Beispiele für den Gebrauch:
Beispiele für den Gebrauch:




Wenn die LAPLACE-Bedingung






a)  Bestimmen der Wahrscheinlichkeiten für die gegebenen Ereignisse
Der Aufgabenstellung kannst du entnehmen, dass die Zuschauerzahlen in der Fußball-Bundesliga in der Saison 2011/12 einen Rekord erreichten. In dieser Saison waren pro Spiel durchschnittlich mehr als 40.000 Zuschauer, wobei das Publikum mittlerweile zu 25 % weiblich ist. Weiterhin kannst du der Aufgabenstellung entnehmen, dass dieser Prozentsatz im Folgenden als Wahrscheinlichkeit verwendet werden soll. Das heißt:
Mit einer Wahrscheinlichkeit von 25 % ist der Zuschauer eines Bundesliga-Spiels weiblich.
Die Aufgabe gibt dir weiterhin 3 Ereignisse vor, zu welchen du die Wahrscheinlichkeiten berechnen sollst. Diese Ereignisse lauten:
Unter 200 bei einem Bundesliga-Spiel ausgewählten Zuschauern, befinden sich
Bestimmen der Wahrscheinlichkeiten für die gegebenen Ereignisse
Der Aufgabenstellung kannst du entnehmen, dass die Zuschauerzahlen in der Fußball-Bundesliga in der Saison 2011/12 einen Rekord erreichten. In dieser Saison waren pro Spiel durchschnittlich mehr als 40.000 Zuschauer, wobei das Publikum mittlerweile zu 25 % weiblich ist. Weiterhin kannst du der Aufgabenstellung entnehmen, dass dieser Prozentsatz im Folgenden als Wahrscheinlichkeit verwendet werden soll. Das heißt:
Mit einer Wahrscheinlichkeit von 25 % ist der Zuschauer eines Bundesliga-Spiels weiblich.
Die Aufgabe gibt dir weiterhin 3 Ereignisse vor, zu welchen du die Wahrscheinlichkeiten berechnen sollst. Diese Ereignisse lauten:
Unter 200 bei einem Bundesliga-Spiel ausgewählten Zuschauern, befinden sich
 , welche die Anzahl der weiblichen Zuschauer unter den 200 befragten repräsentiert. Da die Zufallsvariable
, welche die Anzahl der weiblichen Zuschauer unter den 200 befragten repräsentiert. Da die Zufallsvariable  mit
mit
 hier als binomialverteilt angenommen werden.
hier als binomialverteilt angenommen werden.  ist also mit
ist also mit  und
und  binomialverteilt.
Berechnen der Wahrscheinlichkeit für Ereignis (1)
Mit der Zufallsvariable
binomialverteilt.
Berechnen der Wahrscheinlichkeit für Ereignis (1)
Mit der Zufallsvariable  kannst du nun die Wahrscheinlichkeit für das erste Ereignis berechnen. Dieses lautete:
Unter 200 bei einem Bundesliga-Spiel ausgewählten Zuschauern befinden sich genau 48 weibliche Zuschauer.
Das heißt, hier musst du die Wahrscheinlichkeit dafür berechnen, dass
kannst du nun die Wahrscheinlichkeit für das erste Ereignis berechnen. Dieses lautete:
Unter 200 bei einem Bundesliga-Spiel ausgewählten Zuschauern befinden sich genau 48 weibliche Zuschauer.
Das heißt, hier musst du die Wahrscheinlichkeit dafür berechnen, dass  einen Wert von 48 annimmt. In Formeln ausgedrückt also:
einen Wert von 48 annimmt. In Formeln ausgedrückt also:
 Beim Lösen dieser Aufgabe gibt es hier 2 Wege, die Berechnung mit deinem GTR und die Lösung mit der Tabelle zur kumulierten Binomialverteilung. Im Folgenden werden beide Lösungswege ausgeführt.
Beim Lösen dieser Aufgabe gibt es hier 2 Wege, die Berechnung mit deinem GTR und die Lösung mit der Tabelle zur kumulierten Binomialverteilung. Im Folgenden werden beide Lösungswege ausgeführt.
 Lösungsweg A: Lösen mit dem GTR
Willst du diese Aufgabe mit deinem GTR lösen, so wählst du hier den binompdf-Befehl, welchen du unter
Lösungsweg A: Lösen mit dem GTR
Willst du diese Aufgabe mit deinem GTR lösen, so wählst du hier den binompdf-Befehl, welchen du unter
 hier zu berechnen, wendest du diesen Befehl wie in den Schaubildern unten an.
hier zu berechnen, wendest du diesen Befehl wie in den Schaubildern unten an.
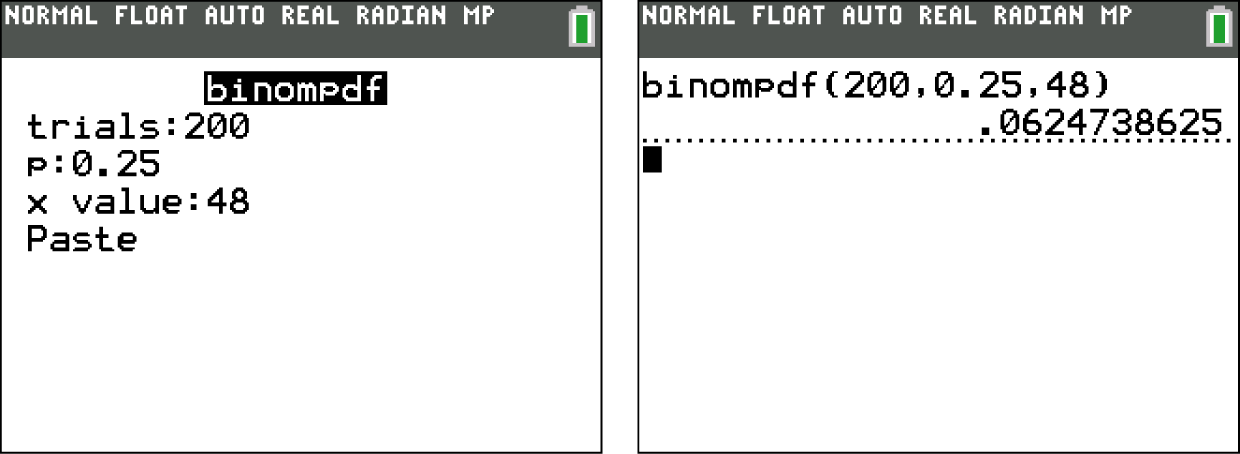
 Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Willst du die Wahrscheinlichkeit
Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Willst du die Wahrscheinlichkeit  mit der Tabelle zur kumulierten Binomialverteilung berechnen, so betrachtest du hier die Tabelle mit
mit der Tabelle zur kumulierten Binomialverteilung berechnen, so betrachtest du hier die Tabelle mit  und
und  . Da dir die Tabelle zur kumulierten Binomialverteilung nur die Wahrscheinlichkeiten
. Da dir die Tabelle zur kumulierten Binomialverteilung nur die Wahrscheinlichkeiten  angibt, musst du hier den gesuchten Wert
angibt, musst du hier den gesuchten Wert  über folgende Differenz berechnen:
über folgende Differenz berechnen:
 Es ergibt sich hier also folgende Berechnung:
Es ergibt sich hier also folgende Berechnung:
 Die Wahrscheinlichkeit dafür, dass genau 48 der befragten Personen weiblich sind, liegt also bei 0,0625 bzw. 6,25%.
Berechnen der Wahrscheinlichkeit für Ereignis (2)
Ereignis (2) war gegeben mit:
Unter den 200 befragten Zuschauern befinden sich mindestens 35 und höchstens 60 weibliche Zuschauer.
Auch hier betrachtest du wieder die Zufallsvariable
Die Wahrscheinlichkeit dafür, dass genau 48 der befragten Personen weiblich sind, liegt also bei 0,0625 bzw. 6,25%.
Berechnen der Wahrscheinlichkeit für Ereignis (2)
Ereignis (2) war gegeben mit:
Unter den 200 befragten Zuschauern befinden sich mindestens 35 und höchstens 60 weibliche Zuschauer.
Auch hier betrachtest du wieder die Zufallsvariable  . Willst du hier die Wahrscheinlichkeit für das gegebene Ereignis berechnen, so muss für
. Willst du hier die Wahrscheinlichkeit für das gegebene Ereignis berechnen, so muss für  gelten:
gelten:
 Du musst also die Wahrscheinlichkeit dafür berechnen, dass
Du musst also die Wahrscheinlichkeit dafür berechnen, dass  nur Werte zwischen 35 und 60 annimmt. Um die Wahrscheinlichkeit dafür zu berechnen, dass
nur Werte zwischen 35 und 60 annimmt. Um die Wahrscheinlichkeit dafür zu berechnen, dass  einen Wert zwischen 35 und 60 annimmt, musst du von der Wahrscheinlichkeit, dass
einen Wert zwischen 35 und 60 annimmt, musst du von der Wahrscheinlichkeit, dass  einen Wert von kleiner gleich 60 annimmt, die Wahrscheinlichkeit dafür subtrahieren, dass
einen Wert von kleiner gleich 60 annimmt, die Wahrscheinlichkeit dafür subtrahieren, dass  eine Wahrscheinlichkeit kleiner gleich 34 annimmt.
Hast du die Wahrscheinlichkeit wie folgt umgeformt, so kannst du zur Berechnung deinen GTR bzw. die Tabelle zur kumulierten Binomialverteilung verwenden.
eine Wahrscheinlichkeit kleiner gleich 34 annimmt.
Hast du die Wahrscheinlichkeit wie folgt umgeformt, so kannst du zur Berechnung deinen GTR bzw. die Tabelle zur kumulierten Binomialverteilung verwenden.

 Lösungsweg A: Lösen mit dem GTR
Willst du diese Aufgabe mit deinem GTR lösen, so wählst du hier den binompdf-Befehl, welchen du im STAT-Menü unter
Lösungsweg A: Lösen mit dem GTR
Willst du diese Aufgabe mit deinem GTR lösen, so wählst du hier den binompdf-Befehl, welchen du im STAT-Menü unter
 ,
,  und schließlich
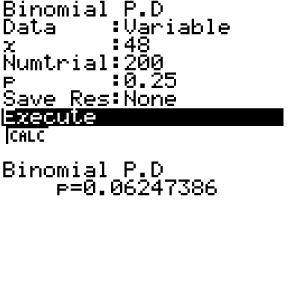
und schließlich  hier zu berechnen, wendest du diesen Befehl wie in den Schaubildern unten an. Dabei ist im linken Schaubild exemplarisch das Berechnen von
hier zu berechnen, wendest du diesen Befehl wie in den Schaubildern unten an. Dabei ist im linken Schaubild exemplarisch das Berechnen von  dargestellt.
dargestellt.
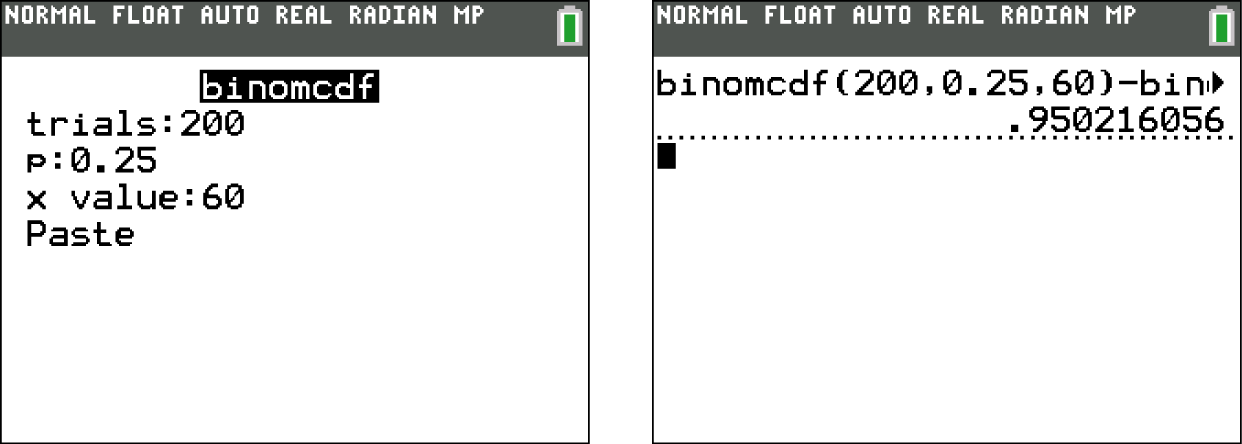 Es folgt also:
Es folgt also:
 .
.
 Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Auch hier betrachtest du wieder die Tabelle mit
Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Auch hier betrachtest du wieder die Tabelle mit  und
und  . Suche die Werte zu
. Suche die Werte zu  und
und  in der Tabelle und berechne die gesuchte Wahrscheinlichkeit über die folgende Differenz:
in der Tabelle und berechne die gesuchte Wahrscheinlichkeit über die folgende Differenz:
 Die Wahrscheinlichkeit dafür, dass sich mindestens 35 und höchstens 60 weibliche Zuschauer unter den 200 befragten Zuschauern befinden, beträgt also 0,9502 bzw. 95,02 %.
Berechnen der Wahrscheinlichkeit für Ereignis (3)
Ereignis (3) war gegeben mit:
Unter den 200 befragten Zuschauern befindet sich eine Anzahl von weiblichen Zuschauern, die um mindestens 10 von ihrem Erwartungswert abweicht.
Da hier mit
Die Wahrscheinlichkeit dafür, dass sich mindestens 35 und höchstens 60 weibliche Zuschauer unter den 200 befragten Zuschauern befinden, beträgt also 0,9502 bzw. 95,02 %.
Berechnen der Wahrscheinlichkeit für Ereignis (3)
Ereignis (3) war gegeben mit:
Unter den 200 befragten Zuschauern befindet sich eine Anzahl von weiblichen Zuschauern, die um mindestens 10 von ihrem Erwartungswert abweicht.
Da hier mit  eine binomialverteilte Zufallsvariable vorliegt, berechnet sich deren Erwartungswert über die folgende Formel:
eine binomialverteilte Zufallsvariable vorliegt, berechnet sich deren Erwartungswert über die folgende Formel:
 Hast du den Erwartungswert
Hast du den Erwartungswert  von
von  berechnet, so musst du die Wahrscheinlichkeit für die Abweichung um 10 von diesem berechnen. Eine Abweichung um 10 vom Erwartungswert schließt dabei eine Abweichung nach oben und nach unten ein. Die hier gesuchte Wahrscheinlichkeit
berechnet, so musst du die Wahrscheinlichkeit für die Abweichung um 10 von diesem berechnen. Eine Abweichung um 10 vom Erwartungswert schließt dabei eine Abweichung nach oben und nach unten ein. Die hier gesuchte Wahrscheinlichkeit  ergibt sich also über folgenden Ansatz:
ergibt sich also über folgenden Ansatz:
 %LT Der Erwartungswert von
%LT Der Erwartungswert von  ist hier:
ist hier:
 .
Willst du die hier vorliegende Wahrscheinlichkeit wie oben berechnen, so musst du diese auch hier zunächst wie folgt mit dem Gegenereignis umformen:
.
Willst du die hier vorliegende Wahrscheinlichkeit wie oben berechnen, so musst du diese auch hier zunächst wie folgt mit dem Gegenereignis umformen:

 Lösungsweg A: Lösen mit dem GTR
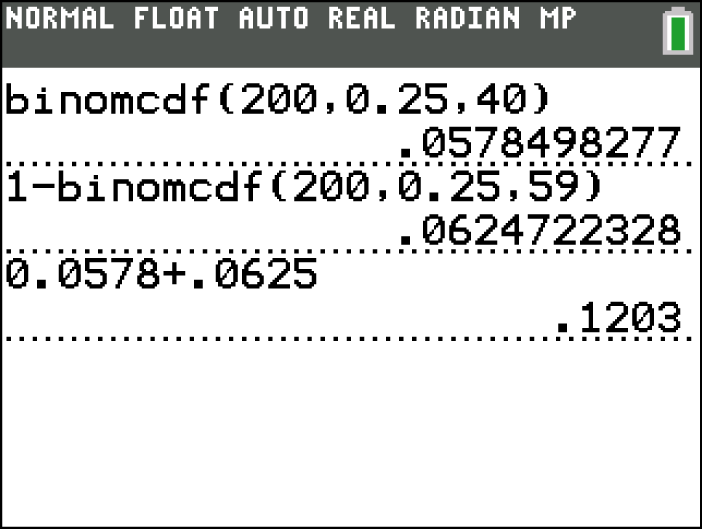
Willst du auch diese Aufgabe mit deinem GTR lösen, so wählst du hier wieder den binomcdf-Befehl. Die hier gesuchte Wahrscheinlichkeit wird im Schaubild unten berechnet, wobei wie in den vorherigen Aufgabenteilen vorgegangen wird.
Lösungsweg A: Lösen mit dem GTR
Willst du auch diese Aufgabe mit deinem GTR lösen, so wählst du hier wieder den binomcdf-Befehl. Die hier gesuchte Wahrscheinlichkeit wird im Schaubild unten berechnet, wobei wie in den vorherigen Aufgabenteilen vorgegangen wird.
 Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Auch hier betrachtest du wieder die Tabelle mit
Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Auch hier betrachtest du wieder die Tabelle mit  und
und  . Suche die Werte zu
. Suche die Werte zu  und
und  in der Tabelle und berechne die gesuchte Wahrscheinlichkeit über die folgende Summe:
in der Tabelle und berechne die gesuchte Wahrscheinlichkeit über die folgende Summe:
 Die Wahrscheinlichkeit dafür, dass die Anzahl der weiblichen Zuschauer um mindestens 10 vom Erwartungswert abweicht, beträgt also 0,1203 bzw. 12,03%.
Die Wahrscheinlichkeit dafür, dass die Anzahl der weiblichen Zuschauer um mindestens 10 vom Erwartungswert abweicht, beträgt also 0,1203 bzw. 12,03%.
- (1) genau 48 weibliche Zuschauer.
- (2) mindestens 35 und höchstens 60 weibliche Zuschauer.
- (3) eine Anzahl von weiblichen Zuschauern, die um mindestens 10 von ihrem Erwartungswert abweicht.
- „Zuschauer ist weiblich“
- „Zuschauer ist nicht weiblich“
2nd  VARS (DISTR)
VARS (DISTR)  A: binompdf(
A: binompdf(
findest. Um 
2nd  VARS (DISTR)
VARS (DISTR)  B:binompdf(
B:binompdf(
findest. Um 

b)  Ereignis
Ereignis  im Sachzusammenhang beschreiben
Hier sollst du nun ein Ereignis
im Sachzusammenhang beschreiben
Hier sollst du nun ein Ereignis  im Sachzusammenhang beschreiben, dessen Wahrscheinlichkeit durch den folgenden Term berechnet werden kann:
im Sachzusammenhang beschreiben, dessen Wahrscheinlichkeit durch den folgenden Term berechnet werden kann:
 Den Wert des Terms musst du dabei aber nicht berechnen. Du kannst dir dabei zunächst überlegen, was der Term im mathematischen Sinn bedeutet und dies anschließend auf den Sachzusammenhang übertragen.
Den Wert des Terms musst du dabei aber nicht berechnen. Du kannst dir dabei zunächst überlegen, was der Term im mathematischen Sinn bedeutet und dies anschließend auf den Sachzusammenhang übertragen.
Hierfür kannst du den Term in zwei Teile aufteilen und dir zunächst für diese beiden einzelnen Teile klarmachen, was sie bedeuten.


 1. Schritt: Mathematische Bedeutung
Der grüne Teil 1- zeigt dir an, dass es hier um die Berechnung der Wahrscheinlichkeit eines Gegenereignisses geht. Und zwar berechnet
1. Schritt: Mathematische Bedeutung
Der grüne Teil 1- zeigt dir an, dass es hier um die Berechnung der Wahrscheinlichkeit eines Gegenereignisses geht. Und zwar berechnet  die Wahrscheinlichkeit des Gegenereignisses
die Wahrscheinlichkeit des Gegenereignisses  , dessen Wahrscheinlichkeit durch den zweiten (roten) Teil des Terms berechnet wird.
Der rote Teil des Terms hat eine bestimmte Form. Diese Form sollte dir bekannt vorkommen. Sie hat Ähnlichkeiten mit der Formel für die kumulierte Binomialverteilung, die du im vorherigen Aufgabenteil bereits in Form der Tabelle verwendet hast.
Du weißt, dass für eine binomialverteilte Zufallsvariable
, dessen Wahrscheinlichkeit durch den zweiten (roten) Teil des Terms berechnet wird.
Der rote Teil des Terms hat eine bestimmte Form. Diese Form sollte dir bekannt vorkommen. Sie hat Ähnlichkeiten mit der Formel für die kumulierte Binomialverteilung, die du im vorherigen Aufgabenteil bereits in Form der Tabelle verwendet hast.
Du weißt, dass für eine binomialverteilte Zufallsvariable  mit den Parametern
mit den Parametern  und
und  gilt:
gilt:
 Hier beschreibt der Term
Hier beschreibt der Term
 demnach die Wahrscheinlichkeit
demnach die Wahrscheinlichkeit  einer Zufallsvariablen
einer Zufallsvariablen  , die binomialverteilt ist mit den Parametern
, die binomialverteilt ist mit den Parametern  und
und  . Dabei sind
. Dabei sind  und
und  :
:

 Insgesamt ist damit
Insgesamt ist damit  . Diesen Term kannst du mit Hilfe des Gegenereignisses umformulieren und erhältst:
. Diesen Term kannst du mit Hilfe des Gegenereignisses umformulieren und erhältst:
 Damit beschreibt
Damit beschreibt  also die Wahrscheinlichkeit dafür, dass eine binomialverteilte Zufallsvariable
also die Wahrscheinlichkeit dafür, dass eine binomialverteilte Zufallsvariable  mit den Parametern
mit den Parametern  und
und  , mindestens den Wert
, mindestens den Wert  annimmt.
2. Schritt: Übertragung auf den Sachzusammenhang
Dir fällt auf, dass die oben genannte Zufallsvariable
annimmt.
2. Schritt: Übertragung auf den Sachzusammenhang
Dir fällt auf, dass die oben genannte Zufallsvariable  binomialverteilt ist, mit der Wahrscheinlichkeit
binomialverteilt ist, mit der Wahrscheinlichkeit  und dem Stichprobenumfang
und dem Stichprobenumfang  .
.
Im gegebenen Sachzusammenhang beträgt die Wahrscheinlichkeit dafür, dass ein Zuschauer weiblich ist, ebenfalls .
.
Die Zufallsvariable kann also als Zufallsvariable betrachtet werden, die die zufällige Anzahl an weiblichen Zuschauern unter
kann also als Zufallsvariable betrachtet werden, die die zufällige Anzahl an weiblichen Zuschauern unter  Besuchern des untersuchten Bundesliga-Spiels beschreibt.
Damit ist
Besuchern des untersuchten Bundesliga-Spiels beschreibt.
Damit ist  die Wahrscheinlichkeit dafür, dass sich unter den
die Wahrscheinlichkeit dafür, dass sich unter den  zufällig ausgewählten Zuschauern des Bundesliga-Spiels mehr als 300 weibliche Zuschauer befinden.
Demnach beschreibt
zufällig ausgewählten Zuschauern des Bundesliga-Spiels mehr als 300 weibliche Zuschauer befinden.
Demnach beschreibt  das Ereignis, dass sich unter den
das Ereignis, dass sich unter den  zufällig ausgewählten Zuschauern des Bundesliga-Spiels mehr als 300 weibliche Zuschauer befinden.
zufällig ausgewählten Zuschauern des Bundesliga-Spiels mehr als 300 weibliche Zuschauer befinden.
Hierfür kannst du den Term in zwei Teile aufteilen und dir zunächst für diese beiden einzelnen Teile klarmachen, was sie bedeuten.
Im gegebenen Sachzusammenhang beträgt die Wahrscheinlichkeit dafür, dass ein Zuschauer weiblich ist, ebenfalls
Die Zufallsvariable
c) (1)  Ermitteln des zum Erwartungswert symmetrischen Intervalls
Der Aufgabenstellung kannst du jetzt entnehmen, dass bei einem Bundesliga-Spiel 20.000 Zuschauer ins Stadion strömen. An die weiblichen Zuschauer soll dabei ein Flyer verteilt werden, welcher auf ein spezielles Getränkeangebot hinweist.
Deine Aufgabe ist es dabei zunächst, auf Grundlage der 20.000 Zuschauer, das zum Erwartungswert symmetrische Intervall kleinster Länge zu bestimmen, in dem die Anzahl der weiblichen Zuschauer mit einer Wahrscheinlichkeit von mindestens 0,9 bzw. 90 % liegt.
Willst du diese Aufgabe hier lösen, so betrachtest du die Zufallsvariable
Ermitteln des zum Erwartungswert symmetrischen Intervalls
Der Aufgabenstellung kannst du jetzt entnehmen, dass bei einem Bundesliga-Spiel 20.000 Zuschauer ins Stadion strömen. An die weiblichen Zuschauer soll dabei ein Flyer verteilt werden, welcher auf ein spezielles Getränkeangebot hinweist.
Deine Aufgabe ist es dabei zunächst, auf Grundlage der 20.000 Zuschauer, das zum Erwartungswert symmetrische Intervall kleinster Länge zu bestimmen, in dem die Anzahl der weiblichen Zuschauer mit einer Wahrscheinlichkeit von mindestens 0,9 bzw. 90 % liegt.
Willst du diese Aufgabe hier lösen, so betrachtest du die Zufallsvariable  , die die Anzahl der Frauen im Stadion beschreibt. Da sich insgesamt 20.000 Zuschauer im Stadion befinden, gilt für
, die die Anzahl der Frauen im Stadion beschreibt. Da sich insgesamt 20.000 Zuschauer im Stadion befinden, gilt für  :
:  . Weiterhin gilt für die Zufallsvariable
. Weiterhin gilt für die Zufallsvariable  , dass die Wahrscheinlichkeit, für das Befragen einer Frau bei 0,25 bzw. 25 % liegt (siehe Aufgabe zuvor).
Nun sollst du ein 90 %-Konfidenzintervall um den Erwartungswert von
, dass die Wahrscheinlichkeit, für das Befragen einer Frau bei 0,25 bzw. 25 % liegt (siehe Aufgabe zuvor).
Nun sollst du ein 90 %-Konfidenzintervall um den Erwartungswert von  bilden.
Zum Lösen dieser, musst du hier die
bilden.
Zum Lösen dieser, musst du hier die  -Regeln anwenden. Gehe dabei so vor:
-Regeln anwenden. Gehe dabei so vor:
 und
und  ergibt sich
ergibt sich
 .
Damit ist das Laplace-Kriterium für die Zufallsvariable
.
Damit ist das Laplace-Kriterium für die Zufallsvariable  erfüllt und die Sigma-Regeln dürfen angewandt werden.
2. Schritt:
erfüllt und die Sigma-Regeln dürfen angewandt werden.
2. Schritt:  -Regeln umformen
Setze nun wie oben beschrieben in den Ausdruck
-Regeln umformen
Setze nun wie oben beschrieben in den Ausdruck  ein und berechne wie folgt das gesuchte Intervall
ein und berechne wie folgt das gesuchte Intervall
 Das hier gesuchte Intervall ist:
Das hier gesuchte Intervall ist: ![\(\left[4.899;5.101\right]\)](https://mathjax.schullv.de/f783f67e6ca0667e9704b5edaaf0075279cfd88c3cfa8cb894d4cfad3764a85a?color=5a5a5a) .
.
- Berechne zunächst die Standardabweichung von
und stelle mit dieser sicher, ob das Laplace-Kriterium
erfüllt ist.
- Du findest die Regel
- Setze
und
- Forme so weit wie möglich um und ermittle so das gesuchte Intervall.
c) (2)  Voraussetzung, mit der die Wahrscheinlichkeit berechnet werden kann
Der Aufgabenstellung kannst du nun entnehmen, dass sich vor einem Kassenhäuschen eine Schlange von 50 Zuschauern gebildet hat. Deine Aufgabe ist es nun, die Voraussetzung zu nennen, unter der die Wahrscheinlichkeit
Voraussetzung, mit der die Wahrscheinlichkeit berechnet werden kann
Der Aufgabenstellung kannst du nun entnehmen, dass sich vor einem Kassenhäuschen eine Schlange von 50 Zuschauern gebildet hat. Deine Aufgabe ist es nun, die Voraussetzung zu nennen, unter der die Wahrscheinlichkeit  , dass sich in der Schlange 12 weibliche Zuschauer befinden, so berechnet werden kann:
, dass sich in der Schlange 12 weibliche Zuschauer befinden, so berechnet werden kann:
 P= \dbinom{50}{12} \cdot 0,25^{12} \cdot 0,75^{38}
P= \dbinom{50}{12} \cdot 0,25^{12} \cdot 0,75^{38}  Betrachtest du den gegebenen Term genauer, so kannst du erkennen, dass es sich hier um den Ansatz zur Berechnung der Wahrscheinlichkeit einer binomialverteilten Zufallsvariablen handelt. Mit diesem Term können Wahrscheinlichkeiten der Form
Betrachtest du den gegebenen Term genauer, so kannst du erkennen, dass es sich hier um den Ansatz zur Berechnung der Wahrscheinlichkeit einer binomialverteilten Zufallsvariablen handelt. Mit diesem Term können Wahrscheinlichkeiten der Form  für ein bestimmtes
für ein bestimmtes  berechnet werden. Das heißt, die hier gesuchten Voraussetzungen ergeben sich aus den Voraussetzungen für eine binomialverteilte Zufallsvariable.
Damit die Wahrscheinlichkeit hier mit Hilfe der Binomialverteilung berechnet werden kann, muss es sich um ein Ziehen mit Zurücklegen handeln. Das heißt die Wahrscheinlichkeit dafür, dass die Person, die vor dem Kassenhäuschen als nächstes steht, eine Frau ist, muss immer die gleiche sein und darf sich nicht im Laufe des Experiments verändern. Weiterhin darf die hier betrachtete Zufallsvariable nur zwei mögliche Ausprägungen besitzen, es darf also nur zwischen Mann und Frau und nicht z.B. Mann, Frau und Kind unterschieden werden.
berechnet werden. Das heißt, die hier gesuchten Voraussetzungen ergeben sich aus den Voraussetzungen für eine binomialverteilte Zufallsvariable.
Damit die Wahrscheinlichkeit hier mit Hilfe der Binomialverteilung berechnet werden kann, muss es sich um ein Ziehen mit Zurücklegen handeln. Das heißt die Wahrscheinlichkeit dafür, dass die Person, die vor dem Kassenhäuschen als nächstes steht, eine Frau ist, muss immer die gleiche sein und darf sich nicht im Laufe des Experiments verändern. Weiterhin darf die hier betrachtete Zufallsvariable nur zwei mögliche Ausprägungen besitzen, es darf also nur zwischen Mann und Frau und nicht z.B. Mann, Frau und Kind unterschieden werden.
 Entscheiden, ob Berechnung hier zulässig ist
Nun sollst du zusätzlich entscheiden, ob die Berechnung der Wahrscheinlichkeit in der vorliegenden Situation zulässig ist. Stelle dir dazu die Frage, ob die Anzahl der Frauen unter den 50 Personen vor dem Kassenhäuschen als binomialverteilt angenommen werden kann. Dazu musst du dir die Frage stellen, ob es sich hier wirklich um ein Ziehen mit Zurücklegen handelt.
Würde es sich hier nicht um ein Ziehen mit Zurücklegen handeln, so würde sich die Wahrscheinlichkeit für das Auftreten einer Frau unter den 50 Personen vor dem Kassenhäuschen ändern, nachdem eine von ihnen vor dem Kassenhäuschen stand.
Die Wahrscheinlichkeit dafür, dass eine Frau ein deutsches Stadion besucht, liegt laut einer Untersuchung bei 25 %. Diese Wahrscheinlichkeit gilt also für alle Stadien in Deutschland. Die Größe ist also „von außen“ bzw. „exogen“ gegeben. Das heißt, die Wahrscheinlichkeit dafür, dass eine Frau vor dem Kassenhäuschen steht, ist immer die gleiche, weshalb hier ein Ziehen mit Zurücklegen vorliegt und die Berechnung über den gegeben Ansatz zulässig ist.
Entscheiden, ob Berechnung hier zulässig ist
Nun sollst du zusätzlich entscheiden, ob die Berechnung der Wahrscheinlichkeit in der vorliegenden Situation zulässig ist. Stelle dir dazu die Frage, ob die Anzahl der Frauen unter den 50 Personen vor dem Kassenhäuschen als binomialverteilt angenommen werden kann. Dazu musst du dir die Frage stellen, ob es sich hier wirklich um ein Ziehen mit Zurücklegen handelt.
Würde es sich hier nicht um ein Ziehen mit Zurücklegen handeln, so würde sich die Wahrscheinlichkeit für das Auftreten einer Frau unter den 50 Personen vor dem Kassenhäuschen ändern, nachdem eine von ihnen vor dem Kassenhäuschen stand.
Die Wahrscheinlichkeit dafür, dass eine Frau ein deutsches Stadion besucht, liegt laut einer Untersuchung bei 25 %. Diese Wahrscheinlichkeit gilt also für alle Stadien in Deutschland. Die Größe ist also „von außen“ bzw. „exogen“ gegeben. Das heißt, die Wahrscheinlichkeit dafür, dass eine Frau vor dem Kassenhäuschen steht, ist immer die gleiche, weshalb hier ein Ziehen mit Zurücklegen vorliegt und die Berechnung über den gegeben Ansatz zulässig ist.
d)(1)  Gegebene Daten im Baumdiagramm darstellen
Nun ist es deine Aufgabe, die Daten, die du der Aufgabenstellung entnehmen kannst, in das Baumdiagramm einzutragen und die fehlenden relativen Häufigkeiten zu ergänzen.
Dazu kannst du zunächst die Bezeichnungen in die eckigen Kästchen und anschließend die relativen Häufigkeiten in die runden Kästchen eintragen, die du der Aufgabenstellung entnehmen kannst. Anschließend kannst du die fehlenden relativen Häufigkeiten berechnen. Die vier runden Kästchen, die sich jeweils am Ende eines „Astes“, befinden, sind für die Anteile der jeweiligen Gruppe an der Gesamtmitgliederzahl vorgesehen, also beispielsweise, wie groß der Anteil der Frauen im gesamten DFB ist. Die runden Kästchen in der Mitte sind dagegen bedingte relative Häufigkeiten. Hier soll das Feld mit
Gegebene Daten im Baumdiagramm darstellen
Nun ist es deine Aufgabe, die Daten, die du der Aufgabenstellung entnehmen kannst, in das Baumdiagramm einzutragen und die fehlenden relativen Häufigkeiten zu ergänzen.
Dazu kannst du zunächst die Bezeichnungen in die eckigen Kästchen und anschließend die relativen Häufigkeiten in die runden Kästchen eintragen, die du der Aufgabenstellung entnehmen kannst. Anschließend kannst du die fehlenden relativen Häufigkeiten berechnen. Die vier runden Kästchen, die sich jeweils am Ende eines „Astes“, befinden, sind für die Anteile der jeweiligen Gruppe an der Gesamtmitgliederzahl vorgesehen, also beispielsweise, wie groß der Anteil der Frauen im gesamten DFB ist. Die runden Kästchen in der Mitte sind dagegen bedingte relative Häufigkeiten. Hier soll das Feld mit  beispielsweise den Anteil der Mädchen unter allen weiblichen Mitgliedern angeben.
Die Zuschauer werden zunächst in „weiblich“ und „ männlich“ unterschieden. Anschließend werden diese beiden Gruppen jeweils wieder in zwei unterschiedliche Altersgruppen eingeteilt. Bei den weiblichen Zuschauern sind dies „Frauen“ und „Mädchen“, bei den männlichen „Senioren“ und „Junioren“.
Die Bezeichnungen müssen demnach wie folgt eingetragen werden:
beispielsweise den Anteil der Mädchen unter allen weiblichen Mitgliedern angeben.
Die Zuschauer werden zunächst in „weiblich“ und „ männlich“ unterschieden. Anschließend werden diese beiden Gruppen jeweils wieder in zwei unterschiedliche Altersgruppen eingeteilt. Bei den weiblichen Zuschauern sind dies „Frauen“ und „Mädchen“, bei den männlichen „Senioren“ und „Junioren“.
Die Bezeichnungen müssen demnach wie folgt eingetragen werden:
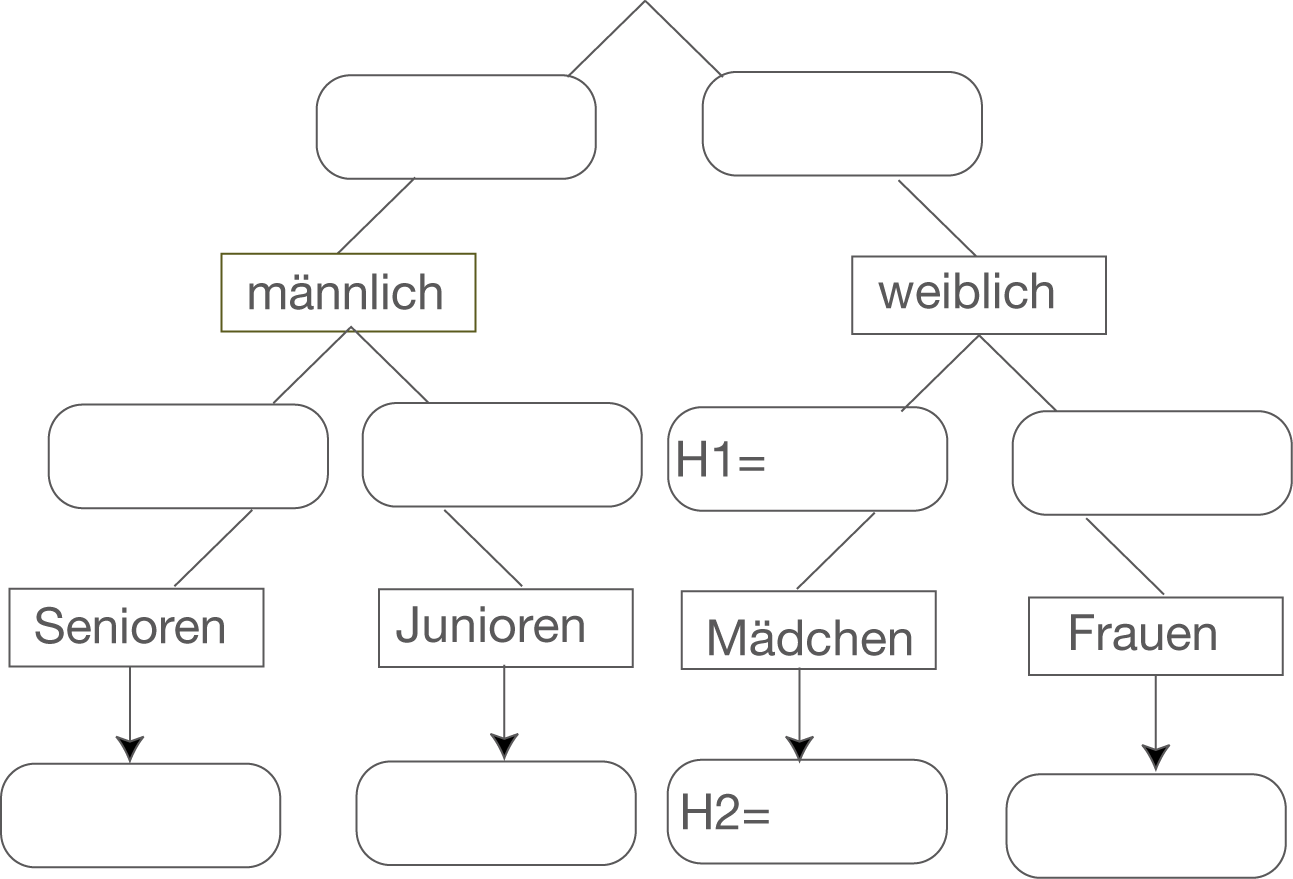 Nun kannst du die relativen Häufigkeiten eintragen, die du der Aufgabenstellung bereits entnehmen kannst. Damit ergibt sich dann das folgende Diagramm:
Nun kannst du die relativen Häufigkeiten eintragen, die du der Aufgabenstellung bereits entnehmen kannst. Damit ergibt sich dann das folgende Diagramm:
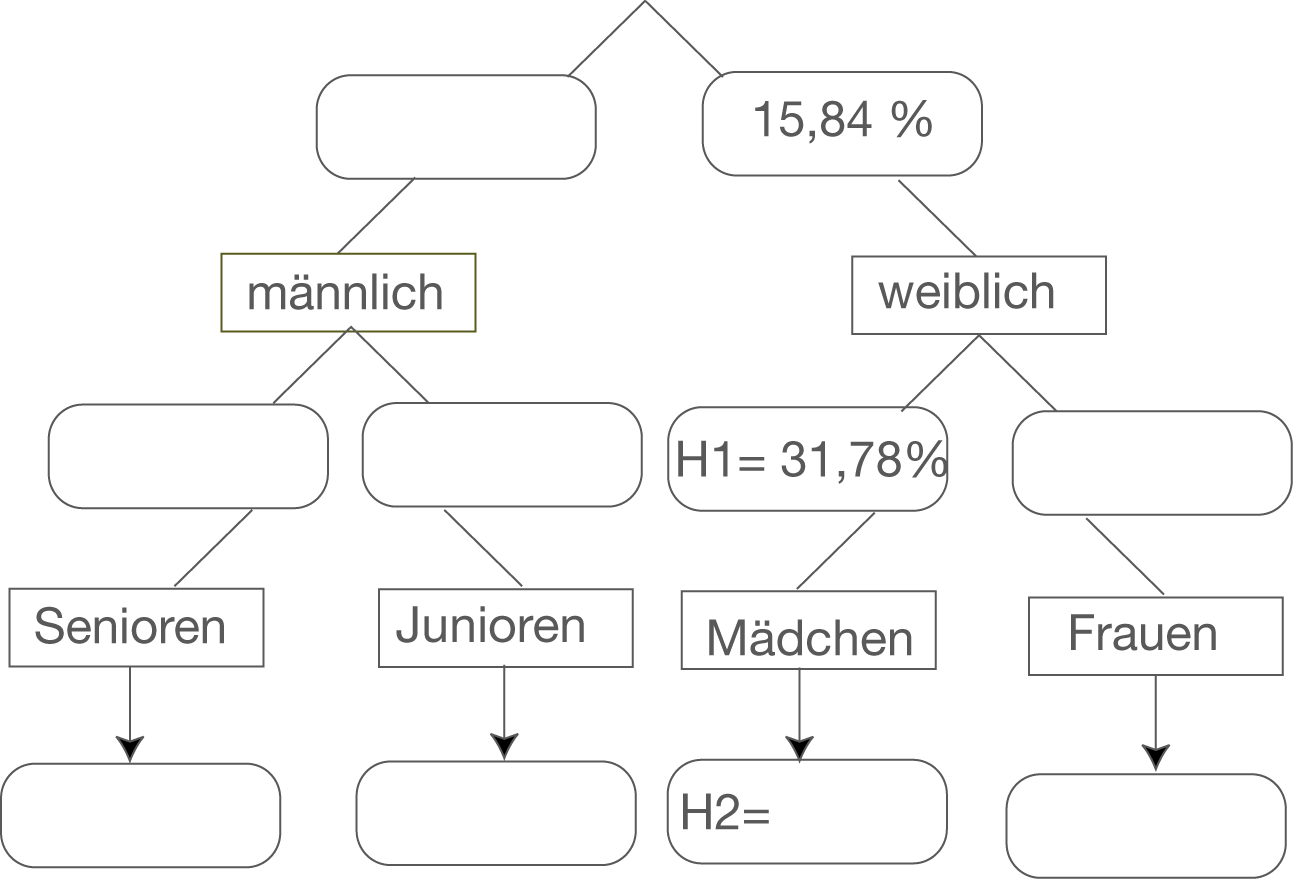 Nun kannst du die fehlenden relativen Häufigkeiten berechnen.
Da ein Mitglied entweder weiblich oder männlich ist, weder beides noch keins von beidem sein kann, muss der Anteil
Nun kannst du die fehlenden relativen Häufigkeiten berechnen.
Da ein Mitglied entweder weiblich oder männlich ist, weder beides noch keins von beidem sein kann, muss der Anteil  der männlichen Mitglieder zusammen mit dem Anteil
der männlichen Mitglieder zusammen mit dem Anteil  der weiblichen Mitglieder
der weiblichen Mitglieder  ergeben. Dadurch erhältst du für den Anteil der männlichen Mitglieder:
ergeben. Dadurch erhältst du für den Anteil der männlichen Mitglieder:
 .
Genauso kannst du auch bei dem Anteil
.
Genauso kannst du auch bei dem Anteil  der Frauen an der Zahl der weiblichen Mitglieder vorgehen, da ein weibliches Mitglied entweder der Altersgruppe der Frauen oder der Altersgruppe der Mädchen angehören muss. Dann erhältst du:
der Frauen an der Zahl der weiblichen Mitglieder vorgehen, da ein weibliches Mitglied entweder der Altersgruppe der Frauen oder der Altersgruppe der Mädchen angehören muss. Dann erhältst du:
 .
Trägst du diese relativen Häufigkeiten ebenfalls ein, so erhältst du folgendes Diagramm:
.
Trägst du diese relativen Häufigkeiten ebenfalls ein, so erhältst du folgendes Diagramm:
 Nun kannst du noch den Anteil
Nun kannst du noch den Anteil  der Frauen an der Gesamtmitgliederzahl berechnen. Dieser ergibt sich mit Hilfe der Pfadmultiplikationsregel durch den Anteil der weiblichen Mitglieder multipliziert mit dem Anteil der Frauen an der Zahl der weiblichen Mitglieder:
der Frauen an der Gesamtmitgliederzahl berechnen. Dieser ergibt sich mit Hilfe der Pfadmultiplikationsregel durch den Anteil der weiblichen Mitglieder multipliziert mit dem Anteil der Frauen an der Zahl der weiblichen Mitglieder:
 .
Genauso kannst du auch den Anteil
.
Genauso kannst du auch den Anteil  der Mädchen an der Gesamtmitgliederzahl berechnen und erhältst:
der Mädchen an der Gesamtmitgliederzahl berechnen und erhältst:
 .
Nun weißt du noch, dass insgesamt ca.
.
Nun weißt du noch, dass insgesamt ca.  der Mitglieder zu den Jugendlichen gehören. Der Anteil der Junioren an der Gesamtmitgliederzahl und der Anteil der Mädchen an der Gesamtmitgliederzahl müssen also zusammen
der Mitglieder zu den Jugendlichen gehören. Der Anteil der Junioren an der Gesamtmitgliederzahl und der Anteil der Mädchen an der Gesamtmitgliederzahl müssen also zusammen  betragen. Damit ergibt sich für den Anteil der Junioren an der Mitgliederzahl:
betragen. Damit ergibt sich für den Anteil der Junioren an der Mitgliederzahl:  .
Als nächstes bietet es sich an, den Anteil
.
Als nächstes bietet es sich an, den Anteil  zu berechnen. Dieser ergibt sich wieder mit Hilfe der Pfadmultiplikationsregel. Es muss gelten:
zu berechnen. Dieser ergibt sich wieder mit Hilfe der Pfadmultiplikationsregel. Es muss gelten:
 .
Setzt du dort die relativen Häufigkeiten ein, die du bereits bestimmt hast, so ergibt sich eine Gleichung, die du nach
.
Setzt du dort die relativen Häufigkeiten ein, die du bereits bestimmt hast, so ergibt sich eine Gleichung, die du nach  lösen kannst:
lösen kannst:
 Trägst du diese berechneten relativen Häufigkeiten in dein Diagramm ein, so sollte es ähnlich aussehen wie hier:
Trägst du diese berechneten relativen Häufigkeiten in dein Diagramm ein, so sollte es ähnlich aussehen wie hier:
 Nun kannst du wie zuvor die beiden übrigen relativen Häufigkeiten berechnen:
Nun kannst du wie zuvor die beiden übrigen relativen Häufigkeiten berechnen:
 .
.
 .
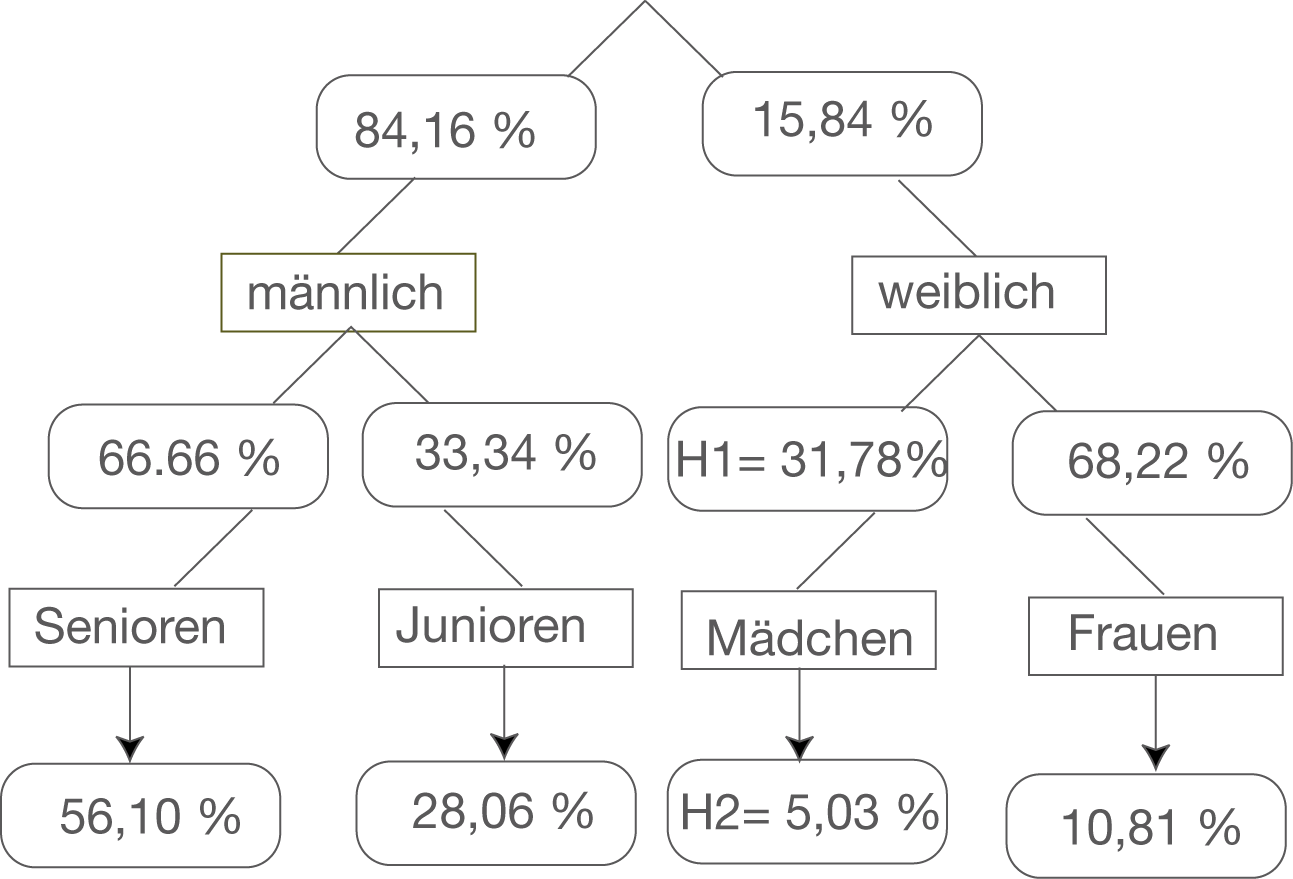
Damit ist das Baumdiagramm nun gefüllt und sollte so aussehen:
.
Damit ist das Baumdiagramm nun gefüllt und sollte so aussehen:
 d) (2)
d) (2)  Relative Häufigkeiten beschreiben
Nun sollst du die beiden relativen Häufigkeiten, die im Baumdiagramm mit
Relative Häufigkeiten beschreiben
Nun sollst du die beiden relativen Häufigkeiten, die im Baumdiagramm mit  und
und  gekennzeichnet sind, mit Worten beschreiben.
gekennzeichnet sind, mit Worten beschreiben.
 gibt den Anteil der Mädchen an, den diese an der Gesamtzahl der weiblichen Mitglieder haben. Also gehören
gibt den Anteil der Mädchen an, den diese an der Gesamtzahl der weiblichen Mitglieder haben. Also gehören  aller weiblichen Mitglieder zur Altersgruppe der Mädchen.
aller weiblichen Mitglieder zur Altersgruppe der Mädchen.
 gibt den Anteil der Mädchen an, den diese an der Gesamtmitgliederzahl haben. Dies bedeutet, dass
gibt den Anteil der Mädchen an, den diese an der Gesamtmitgliederzahl haben. Dies bedeutet, dass  aller Mitglieder des DFB Mädchen sind.
d) (3)
aller Mitglieder des DFB Mädchen sind.
d) (3)  Ermitteln der Wahrscheinlichkeiten
Nun werden zwei Mitglieder des DFB zufällig ausgewählt und du sollst die Wahrscheinlichkeit dafür ermitteln, dass es sich bei den beiden Personen
Ermitteln der Wahrscheinlichkeiten
Nun werden zwei Mitglieder des DFB zufällig ausgewählt und du sollst die Wahrscheinlichkeit dafür ermitteln, dass es sich bei den beiden Personen
 Die Wahrscheinlichkeit dafür, einen „Junior“ und ein „Mädchen“ auszuwählen liegt also bei 0,0282 bzw. 2,82 %.
Die Wahrscheinlichkeit dafür, einen „Junior“ und ein „Mädchen“ auszuwählen liegt also bei 0,0282 bzw. 2,82 %.





- um einen „Junior“
- und ein „Mädchen“ handelt.
- Wahrscheinlichkeit für einen „Junior“:
- Wahrscheinlichkeit für ein „Mädchen“:
e) (1)  Wahl der Nullhypothese begründen
Der Verkaufsleiter führt einen Hypothesentest durch um zu überprüfen, ob der Anteil der weiblichen Stadionbesucher tatsächlich gestiegen ist. Ist dies der Fall, so stellt er mehr Vorräte für die speziellen Angebote für die weiblichen Besucher bereit. Du sollst nun die Wahl seiner Nullhypothese
Wahl der Nullhypothese begründen
Der Verkaufsleiter führt einen Hypothesentest durch um zu überprüfen, ob der Anteil der weiblichen Stadionbesucher tatsächlich gestiegen ist. Ist dies der Fall, so stellt er mehr Vorräte für die speziellen Angebote für die weiblichen Besucher bereit. Du sollst nun die Wahl seiner Nullhypothese  begründen.
Der Aufgabenstellung kannst du entnehmen, dass er möglichst nicht zu viele Vorräte für die speziellen Angebote einkaufen möchte. Ausgehend von dieser Information kannst du nun überlegen, warum es deshalb sinnvoll ist, die Nullhypothese so zu wählen.
Der Verkaufsleiter möchte unbedingt verhindern zu viele Vorräte für die speziellen Angebote zu kaufen und dadurch auf verderblicher Ware sitzen zu bleiben. Er wird also nur davon ausgehen, dass der Anteil der weiblichen Zuschauer tatsächlich auf mehr als
begründen.
Der Aufgabenstellung kannst du entnehmen, dass er möglichst nicht zu viele Vorräte für die speziellen Angebote einkaufen möchte. Ausgehend von dieser Information kannst du nun überlegen, warum es deshalb sinnvoll ist, die Nullhypothese so zu wählen.
Der Verkaufsleiter möchte unbedingt verhindern zu viele Vorräte für die speziellen Angebote zu kaufen und dadurch auf verderblicher Ware sitzen zu bleiben. Er wird also nur davon ausgehen, dass der Anteil der weiblichen Zuschauer tatsächlich auf mehr als  gestiegen ist und dementsprechend mehr Vorräte einkaufen, wenn deutlich mehr weibliche Besucher als erwartet in der Stichprobe gezählt werden. Weil er auf Nummer sicher gehen will, wählt er daher die Nullhypothese
gestiegen ist und dementsprechend mehr Vorräte einkaufen, wenn deutlich mehr weibliche Besucher als erwartet in der Stichprobe gezählt werden. Weil er auf Nummer sicher gehen will, wählt er daher die Nullhypothese  .
.
 Entscheidungsregel ermitteln
Nun sollst du eine Entscheidungsregel ermitteln. Du sollst also auf Grundlage einer Irrtumswahrscheinlichkeit von
Entscheidungsregel ermitteln
Nun sollst du eine Entscheidungsregel ermitteln. Du sollst also auf Grundlage einer Irrtumswahrscheinlichkeit von  ein Intervall bestimmen, sodass der Verkaufsleiter seine Nullhypothese bestätigt sieht, wenn die Anzahl der weiblichen Zuschauer innerhalb dieses Intervalls liegt. Andernfalls wird die Nullhypothese abgelehnt. Die Wahl der Null- und Gegenhypothese ist dir bereits gegeben. Daraus kannst du schließen, dass hier ein rechtsseitiger Hypothesentest durchgeführt wird. Der Annahmebereich hat damit folgende Form:
ein Intervall bestimmen, sodass der Verkaufsleiter seine Nullhypothese bestätigt sieht, wenn die Anzahl der weiblichen Zuschauer innerhalb dieses Intervalls liegt. Andernfalls wird die Nullhypothese abgelehnt. Die Wahl der Null- und Gegenhypothese ist dir bereits gegeben. Daraus kannst du schließen, dass hier ein rechtsseitiger Hypothesentest durchgeführt wird. Der Annahmebereich hat damit folgende Form:
Der Ablehungsbereich hat dementsprechend die Form:
Um eine Entscheidungsregel formulieren zu können, benötigst du also die rechte Grenze des Annahmebereichs, den Wert  . Um diesen zu berechnen, können dir die
. Um diesen zu berechnen, können dir die  -Regeln helfen. Gehe also so vor:
-Regeln helfen. Gehe also so vor:
 welche die Anzahl der weiblichen Zuschauer in der gegebenen Stichprobe vom Umfang 1.000 beschreibt. Die Zufallsvariable
welche die Anzahl der weiblichen Zuschauer in der gegebenen Stichprobe vom Umfang 1.000 beschreibt. Die Zufallsvariable  ist hier wieder mit
ist hier wieder mit  und
und  mit der gleichen Begründung wie in den Aufgabenteilen zuvor binomialverteilt.
2. Schritt: Annahme- und Ablehnungsbereich bestimmen
Um die
mit der gleichen Begründung wie in den Aufgabenteilen zuvor binomialverteilt.
2. Schritt: Annahme- und Ablehnungsbereich bestimmen
Um die  -Regeln anwenden zu können, muss
-Regeln anwenden zu können, muss  gelten. Diesen Wert kannst du mit Hilfe folgender Formel berechnen, die du auch im Anhang mit den
gelten. Diesen Wert kannst du mit Hilfe folgender Formel berechnen, die du auch im Anhang mit den  -Regeln des Aufgabenblattes findest:
-Regeln des Aufgabenblattes findest:
Setzt du dort die entsprechenden Werte  und
und  ein, so erhältst du:
ein, so erhältst du:
 Du kannst hier also die
Du kannst hier also die  -Regeln anwenden.
Passende
-Regeln anwenden.
Passende  -Regel auswählen
Die passende Regel findest du mit Hilfe der Irrtumswahrscheinlichkeit. Diese ist dir mit
-Regel auswählen
Die passende Regel findest du mit Hilfe der Irrtumswahrscheinlichkeit. Diese ist dir mit  gegeben. Da hier ein rechtsseitiger Test durchgeführt wird, soll gelten:
gegeben. Da hier ein rechtsseitiger Test durchgeführt wird, soll gelten:
 also
also  .
Dies kannst du mit Hilfe des Gegenereignisses umformulieren und erhältst:
.
Dies kannst du mit Hilfe des Gegenereignisses umformulieren und erhältst:
 Damit findest du die folgende
Damit findest du die folgende  -Regel:
-Regel:
Grenze  berechnen
Es muss also gelten:
berechnen
Es muss also gelten:  . Den Wert für
. Den Wert für  kennst du bereits. Berechne nun noch
kennst du bereits. Berechne nun noch  mit Hilfe der folgenden Formel:
mit Hilfe der folgenden Formel:
 Damit kannst du nun
Damit kannst du nun  berechnen und erhältst:
berechnen und erhältst:
 Da ein Annahmebereich nur aus ganzzahligen Werten besteht (es kann schließlich keine halben Besucher geben), muss hier gerundet werden. Weil das
Da ein Annahmebereich nur aus ganzzahligen Werten besteht (es kann schließlich keine halben Besucher geben), muss hier gerundet werden. Weil das  der kleinste Wert ist, für den
der kleinste Wert ist, für den  gerade noch
gerade noch  ist, muss hier aufgerundet werden:
ist, muss hier aufgerundet werden:  .
Damit lauten der Annahmebereich und der Ablehnungsbereich wie folgt:
.
Damit lauten der Annahmebereich und der Ablehnungsbereich wie folgt:
![\(A = [0,..,273]\)](https://mathjax.schullv.de/dc3868078bd327c26b2d3e38320e9e0f6f2c34974a205527629d2e639f236b03?color=5a5a5a) und
und ![\(\overline{A} = [274,...,1.000]\)](https://mathjax.schullv.de/c734ef3d60512448aa0bfa1919a3663e8eeff32322b925e9b1c68b4e0c750ea3?color=5a5a5a) 3. Schritt: Entscheidungsregel formulieren
Du weißt, dass der Verkaufsleiter die Nullhypothese ablehnt, wenn
3. Schritt: Entscheidungsregel formulieren
Du weißt, dass der Verkaufsleiter die Nullhypothese ablehnt, wenn  einen Wert aus dem Ablehnungsbereich annimmt. In diesem Fall würde er mehr Vorräte einkaufen, weil er davon ausginge, dass der Anteil der weiblichen Besucher tatsächlich höher als
einen Wert aus dem Ablehnungsbereich annimmt. In diesem Fall würde er mehr Vorräte einkaufen, weil er davon ausginge, dass der Anteil der weiblichen Besucher tatsächlich höher als  ist.
Werden unter den
ist.
Werden unter den  zufällig ausgewählten Fotos mehr als
zufällig ausgewählten Fotos mehr als  weibliche Stadionbesucher gefunden, so lehnt der Verkaufsleiter seine Nullhypothese unter dem Signifikanzniveau
weibliche Stadionbesucher gefunden, so lehnt der Verkaufsleiter seine Nullhypothese unter dem Signifikanzniveau  ab und geht von einem Anteil an weiblichen Personen aus, der höher als
ab und geht von einem Anteil an weiblichen Personen aus, der höher als  ist. In diesem Fall kauft er mehr Vorräte für die speziellen Angebote für Frauen ein.
Werden in der Stichprobe
ist. In diesem Fall kauft er mehr Vorräte für die speziellen Angebote für Frauen ein.
Werden in der Stichprobe  oder weniger Fotos von Frauen gefunden, so geht der Verkaufsleiter bei einer Irrtumswahrscheinlichkeit von
oder weniger Fotos von Frauen gefunden, so geht der Verkaufsleiter bei einer Irrtumswahrscheinlichkeit von  davon aus, dass der Anteil weiblicher Besucher nicht gestiegen ist und immer noch maximal bei
davon aus, dass der Anteil weiblicher Besucher nicht gestiegen ist und immer noch maximal bei  liegt. In diesem Fall kauft der Verkaufsleiter nicht mehr Vorräte als sonst üblich ein.
e) (2)
liegt. In diesem Fall kauft der Verkaufsleiter nicht mehr Vorräte als sonst üblich ein.
e) (2)  Beschreiben des Fehlers 2. Art und Berechnen der Wahrscheinlichkeit
Hier sollst du nun zum obigen Hypothesentest den Fehler 2. Art beschreiben und die Wahrscheinlichkeit für diesen berechnen, für den Fall, dass der Anteil der weiblichen Zuschauer tatsächlich 30 % beträgt.
Beschreiben des Fehlers 2. Art und Berechnen der Wahrscheinlichkeit
Hier sollst du nun zum obigen Hypothesentest den Fehler 2. Art beschreiben und die Wahrscheinlichkeit für diesen berechnen, für den Fall, dass der Anteil der weiblichen Zuschauer tatsächlich 30 % beträgt.
Der Fehler 2. Art beschreibt immer ein Ablehnen der Gegenhypothese, obwohl diese wahr ist. Hier bedeutet das ein Ablehnen der Gegenhypothese obwohl eigentlich
obwohl eigentlich  gilt. Im Sachzusammenhang interpretiert bedeutet das, dass der Anteil der weiblichen Zuschauer in Wirklichkeit über 25 % gestiegen ist, obwohl dies mit dem Hypothesentest widerlegt wurde.
gilt. Im Sachzusammenhang interpretiert bedeutet das, dass der Anteil der weiblichen Zuschauer in Wirklichkeit über 25 % gestiegen ist, obwohl dies mit dem Hypothesentest widerlegt wurde.
Betrachtest du dazu Zufallsvariable die mit
die mit  und
und  die Anzahl der weiblichen Stadionbesucher nach gestiegenem Anteil beschreibt, dann nimmt diese einen Wert aus dem Annahmebereich für die Nullhypothese an, wenn der Fehler 2. Art eintritt.
Willst du die Wahrscheinlichkeit hier berechnen, so musst du also folgenden Term betrachten:
die Anzahl der weiblichen Stadionbesucher nach gestiegenem Anteil beschreibt, dann nimmt diese einen Wert aus dem Annahmebereich für die Nullhypothese an, wenn der Fehler 2. Art eintritt.
Willst du die Wahrscheinlichkeit hier berechnen, so musst du also folgenden Term betrachten:
Verwende dazu auch hier wieder die Tabelle zur kumulierten Binomialverteilung ( ) oder deinen GTR.
) oder deinen GTR.
 Lösungsweg A: Tabelle zur kumulierten Binomialverteilung
Betrachte hier die Tabelle für
Lösungsweg A: Tabelle zur kumulierten Binomialverteilung
Betrachte hier die Tabelle für  und
und  und suche den Wert an der Stelle
und suche den Wert an der Stelle  .
.
Für die Wahrscheinlichkeit ergibt sich also: .
.
 Lösungsweg B: Lösung über GTR
Verwende hier wieder wie in den Aufgabenteilen zuvor deinen GTR. Mit dem binomcdf-Befehl ergibt sich hier:
Lösungsweg B: Lösung über GTR
Verwende hier wieder wie in den Aufgabenteilen zuvor deinen GTR. Mit dem binomcdf-Befehl ergibt sich hier:
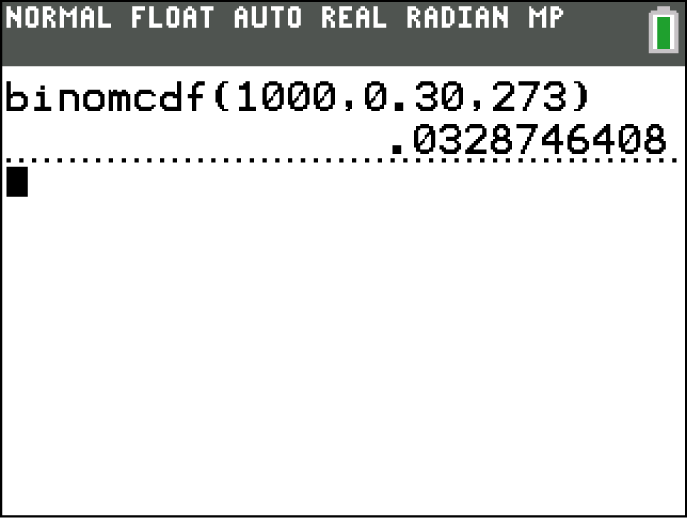 Die Wahrscheinlichkeit für den Fehler 2. Art ist hier also 0,329 bzw. 3,29 %.
Die Wahrscheinlichkeit für den Fehler 2. Art ist hier also 0,329 bzw. 3,29 %.
|
|
|
|
- Führe eine Zufallsvariable
für die Anzahl der weiblichen Zuschauer ein.
- Bestimme den Annahme- und Ablehnungsbereich, indem du die
-Regeln anwendest. Berechne dazu zunächst
um zu überprüfen, ob das Laplace-Kriterium erfüllt ist. Wähle dann die hier passende
-Regel aus und berechne anschließend
. Danach kannst du die Grenzen des Annahme- und Ablehnungsbereichs berechnen.
- Formuliere eine Entscheidungsregel
|
|
|
|
|
{ |
Der Fehler 2. Art beschreibt immer ein Ablehnen der Gegenhypothese, obwohl diese wahr ist. Hier bedeutet das ein Ablehnen der Gegenhypothese
Betrachtest du dazu Zufallsvariable
|
|
Für die Wahrscheinlichkeit ergibt sich also:

a)  Bestimmen der Wahrscheinlichkeiten für die gegebenen Ereignisse
Der Aufgabenstellung kannst du entnehmen, dass die Zuschauerzahlen in der Fußball-Bundesliga in der Saison 2011/12 einen Rekord erreichten. In dieser Saison waren pro Spiel durchschnittlich mehr als 40.000 Zuschauer, wobei das Publikum mittlerweile zu 25 % weiblich ist. Weiterhin kannst du der Aufgabenstellung entnehmen, dass dieser Prozentsatz im Folgenden als Wahrscheinlichkeit verwendet werden soll. Das heißt:
Mit einer Wahrscheinlichkeit von 25 % ist der Zuschauer eines Bundesliga-Spiels weiblich.
Die Aufgabe gibt dir weiterhin 3 Ereignisse vor, zu welchen du die Wahrscheinlichkeiten berechnen sollst. Diese Ereignisse lauten:
Unter 200 bei einem Bundesliga-Spiel ausgewählten Zuschauern, befinden sich
Bestimmen der Wahrscheinlichkeiten für die gegebenen Ereignisse
Der Aufgabenstellung kannst du entnehmen, dass die Zuschauerzahlen in der Fußball-Bundesliga in der Saison 2011/12 einen Rekord erreichten. In dieser Saison waren pro Spiel durchschnittlich mehr als 40.000 Zuschauer, wobei das Publikum mittlerweile zu 25 % weiblich ist. Weiterhin kannst du der Aufgabenstellung entnehmen, dass dieser Prozentsatz im Folgenden als Wahrscheinlichkeit verwendet werden soll. Das heißt:
Mit einer Wahrscheinlichkeit von 25 % ist der Zuschauer eines Bundesliga-Spiels weiblich.
Die Aufgabe gibt dir weiterhin 3 Ereignisse vor, zu welchen du die Wahrscheinlichkeiten berechnen sollst. Diese Ereignisse lauten:
Unter 200 bei einem Bundesliga-Spiel ausgewählten Zuschauern, befinden sich
 , welche die Anzahl der weiblichen Zuschauer unter den 200 befragten repräsentiert. Da die Zufallsvariable
, welche die Anzahl der weiblichen Zuschauer unter den 200 befragten repräsentiert. Da die Zufallsvariable  mit
mit
 hier als binomialverteilt angenommen werden.
hier als binomialverteilt angenommen werden.  ist also mit
ist also mit  und
und  binomialverteilt.
Berechnen der Wahrscheinlichkeit für Ereignis (1)
Mit der Zufallsvariable
binomialverteilt.
Berechnen der Wahrscheinlichkeit für Ereignis (1)
Mit der Zufallsvariable  kannst du nun die Wahrscheinlichkeit für das erste Ereignis berechnen. Dieses lautete:
Unter 200 bei einem Bundesliga-Spiel ausgewählten Zuschauern befinden sich genau 48 weibliche Zuschauer.
Das heißt, hier musst du die Wahrscheinlichkeit dafür berechnen, dass
kannst du nun die Wahrscheinlichkeit für das erste Ereignis berechnen. Dieses lautete:
Unter 200 bei einem Bundesliga-Spiel ausgewählten Zuschauern befinden sich genau 48 weibliche Zuschauer.
Das heißt, hier musst du die Wahrscheinlichkeit dafür berechnen, dass  einen Wert von 48 annimmt. In Formeln ausgedrückt also:
einen Wert von 48 annimmt. In Formeln ausgedrückt also:
 Beim Lösen dieser Aufgabe gibt es hier 2 Wege, die Berechnung mit deinem GTR und die Lösung mit der Tabelle zur kumulierten Binomialverteilung. Im Folgenden werden beide Lösungswege ausgeführt.
Beim Lösen dieser Aufgabe gibt es hier 2 Wege, die Berechnung mit deinem GTR und die Lösung mit der Tabelle zur kumulierten Binomialverteilung. Im Folgenden werden beide Lösungswege ausgeführt.
 Lösungsweg A: Lösen mit dem GTR
Willst du diese Aufgabe mit deinem GTR lösen, so wählst du hier den Bpd-Befehl, welchen du im STAT-Menü unter
Lösungsweg A: Lösen mit dem GTR
Willst du diese Aufgabe mit deinem GTR lösen, so wählst du hier den Bpd-Befehl, welchen du im STAT-Menü unter
 hier zu berechnen, wendest du diesen Befehl wie in den Schaubildern unten an.
hier zu berechnen, wendest du diesen Befehl wie in den Schaubildern unten an.
 Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Willst du die Wahrscheinlichkeit
Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Willst du die Wahrscheinlichkeit  mit der Tabelle zur kumulierten Binomialverteilung berechnen, so betrachtest du hier die Tabelle mit
mit der Tabelle zur kumulierten Binomialverteilung berechnen, so betrachtest du hier die Tabelle mit  und
und  . Da dir die Tabelle zur kumulierten Binomialverteilung nur die Wahrscheinlichkeiten
. Da dir die Tabelle zur kumulierten Binomialverteilung nur die Wahrscheinlichkeiten  angibt, musst du hier den gesuchten Wert
angibt, musst du hier den gesuchten Wert  über folgende Differenz berechnen:
über folgende Differenz berechnen:
 Es ergibt sich hier also folgende Berechnung:
Es ergibt sich hier also folgende Berechnung:
 Die Wahrscheinlichkeit dafür, dass genau 48 der befragten Personen weiblich sind, liegt also bei 0,0625 bzw. 6,25%.
Berechnen der Wahrscheinlichkeit für Ereignis (2)
Ereignis (2) war gegeben mit:
Unter den 200 befragten Zuschauern befinden sich mindestens 35 und höchstens 60 weibliche Zuschauer.
Auch hier betrachtest du wieder die Zufallsvariable
Die Wahrscheinlichkeit dafür, dass genau 48 der befragten Personen weiblich sind, liegt also bei 0,0625 bzw. 6,25%.
Berechnen der Wahrscheinlichkeit für Ereignis (2)
Ereignis (2) war gegeben mit:
Unter den 200 befragten Zuschauern befinden sich mindestens 35 und höchstens 60 weibliche Zuschauer.
Auch hier betrachtest du wieder die Zufallsvariable  . Willst du hier die Wahrscheinlichkeit für das gegebene Ereignis berechnen, so muss für
. Willst du hier die Wahrscheinlichkeit für das gegebene Ereignis berechnen, so muss für  gelten:
gelten:
 Du musst also die Wahrscheinlichkeit dafür berechnen, dass
Du musst also die Wahrscheinlichkeit dafür berechnen, dass  nur Werte zwischen 35 und 60 annimmt. Um die Wahrscheinlichkeit dafür zu berechnen, dass
nur Werte zwischen 35 und 60 annimmt. Um die Wahrscheinlichkeit dafür zu berechnen, dass  einen Wert zwischen 35 und 60 annimmt, musst du von der Wahrscheinlichkeit, dass
einen Wert zwischen 35 und 60 annimmt, musst du von der Wahrscheinlichkeit, dass  einen Wert von kleiner gleich 60 annimmt, die Wahrscheinlichkeit dafür subtrahieren, dass
einen Wert von kleiner gleich 60 annimmt, die Wahrscheinlichkeit dafür subtrahieren, dass  eine Wahrscheinlichkeit kleiner gleich 34 annimmt.
Hast du die Wahrscheinlichkeit wie folgt umgeformt, so kannst du zur Berechnung deinen GTR bzw. die Tabelle zur kumulierten Binomialverteilung verwenden.
eine Wahrscheinlichkeit kleiner gleich 34 annimmt.
Hast du die Wahrscheinlichkeit wie folgt umgeformt, so kannst du zur Berechnung deinen GTR bzw. die Tabelle zur kumulierten Binomialverteilung verwenden.

 Lösungsweg A: Lösen mit dem GTR
Willst du diese Aufgabe mit deinem GTR lösen, so wählst du hier den Bcd-Befehl, welchen du im STAT-Menü unter
Lösungsweg A: Lösen mit dem GTR
Willst du diese Aufgabe mit deinem GTR lösen, so wählst du hier den Bcd-Befehl, welchen du im STAT-Menü unter
 ,
,  und schließlich
und schließlich  hier zu berechnen, wendest du diesen Befehl wie in den Schaubildern unten an. Dabei ist im linken Schaubild exemplarisch das Berechnen von
hier zu berechnen, wendest du diesen Befehl wie in den Schaubildern unten an. Dabei ist im linken Schaubild exemplarisch das Berechnen von  dargestellt.
dargestellt.
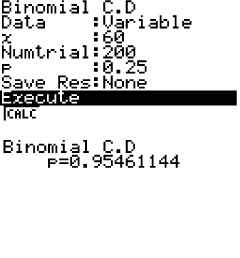 Es folgt also:
Es folgt also:
 .
.
 Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Auch hier betrachtest du wieder die Tabelle mit
Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Auch hier betrachtest du wieder die Tabelle mit  und
und  . Suche die Werte zu
. Suche die Werte zu  und
und  in der Tabelle und berechne die gesuchte Wahrscheinlichkeit über die folgende Differenz:
in der Tabelle und berechne die gesuchte Wahrscheinlichkeit über die folgende Differenz:
 Die Wahrscheinlichkeit dafür, dass sich mindestens 35 und höchstens 60 weibliche Zuschauer unter den 200 befragten Zuschauern befinden, beträgt also 0,9502 bzw. 95,02 %.
Berechnen der Wahrscheinlichkeit für Ereignis (3)
Ereignis (3) war gegeben mit:
Unter den 200 befragten Zuschauern befindet sich eine Anzahl von weiblichen Zuschauern, die um mindestens 10 von ihrem Erwartungswert abweicht.
Da hier mit
Die Wahrscheinlichkeit dafür, dass sich mindestens 35 und höchstens 60 weibliche Zuschauer unter den 200 befragten Zuschauern befinden, beträgt also 0,9502 bzw. 95,02 %.
Berechnen der Wahrscheinlichkeit für Ereignis (3)
Ereignis (3) war gegeben mit:
Unter den 200 befragten Zuschauern befindet sich eine Anzahl von weiblichen Zuschauern, die um mindestens 10 von ihrem Erwartungswert abweicht.
Da hier mit  eine binomialverteilte Zufallsvariable vorliegt, berechnet sich deren Erwartungswert über die folgende Formel:
eine binomialverteilte Zufallsvariable vorliegt, berechnet sich deren Erwartungswert über die folgende Formel:
 Hast du den Erwartungswert
Hast du den Erwartungswert  von
von  berechnet, so musst du die Wahrscheinlichkeit für die Abweichung um 10 von diesem berechnen. Eine Abweichung um 10 vom Erwartungswert schließt dabei eine Abweichung nach oben und nach unten ein. Die hier gesuchte Wahrscheinlichkeit
berechnet, so musst du die Wahrscheinlichkeit für die Abweichung um 10 von diesem berechnen. Eine Abweichung um 10 vom Erwartungswert schließt dabei eine Abweichung nach oben und nach unten ein. Die hier gesuchte Wahrscheinlichkeit  ergibt sich also über folgenden Ansatz:
ergibt sich also über folgenden Ansatz:
 %LT Der Erwartungswert von
%LT Der Erwartungswert von  ist hier:
ist hier:
 .
Willst du die hier vorliegende Wahrscheinlichkeit wie oben berechnen, so musst du diese auch hier zunächst wie folgt mit dem Gegenereignis umformen:
.
Willst du die hier vorliegende Wahrscheinlichkeit wie oben berechnen, so musst du diese auch hier zunächst wie folgt mit dem Gegenereignis umformen:

 Lösungsweg A: Lösen mit dem GTR
Willst du auch diese Aufgabe mit deinem GTR lösen, so wählst du hier wieder den binomcdf-Befehl. Die hier gesuchte Wahrscheinlichkeit wird im Schaubild unten berechnet, wobei wie in den vorherigen Aufgabenteilen vorgegangen wird.
Lösungsweg A: Lösen mit dem GTR
Willst du auch diese Aufgabe mit deinem GTR lösen, so wählst du hier wieder den binomcdf-Befehl. Die hier gesuchte Wahrscheinlichkeit wird im Schaubild unten berechnet, wobei wie in den vorherigen Aufgabenteilen vorgegangen wird.
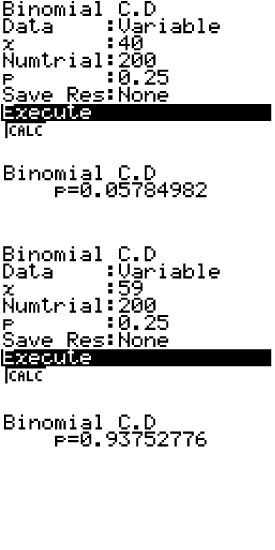 Es folgt:
Es folgt:
 .
.
 Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Auch hier betrachtest du wieder die Tabelle mit
Lösungsweg B: Lösen mit der Tabelle zur kumulierten Binomialverteilung
Auch hier betrachtest du wieder die Tabelle mit  und
und  . Suche die Werte zu
. Suche die Werte zu  und
und  in der Tabelle und berechne die gesuchte Wahrscheinlichkeit über die folgende Summe:
in der Tabelle und berechne die gesuchte Wahrscheinlichkeit über die folgende Summe:
 Die Wahrscheinlichkeit dafür, dass die Anzahl der weiblichen Zuschauer um mindestens 10 vom Erwartungswert abweicht, beträgt also 0,1203 bzw. 12,03%.
Die Wahrscheinlichkeit dafür, dass die Anzahl der weiblichen Zuschauer um mindestens 10 vom Erwartungswert abweicht, beträgt also 0,1203 bzw. 12,03%.
- (1) genau 48 weibliche Zuschauer.
- (2) mindestens 35 und höchstens 60 weibliche Zuschauer.
- (3) eine Anzahl von weiblichen Zuschauern, die um mindestens 10 von ihrem Erwartungswert abweicht.
- „Zuschauer ist weiblich“
- „Zuschauer ist nicht weiblich“
DIST  BINM
BINM  Bpd
Bpd
findest. Um 
DIST  BINM
BINM  Bpd
Bpd
findest. Um 

b)  Ereignis
Ereignis  im Sachzusammenhang beschreiben
Hier sollst du nun ein Ereignis
im Sachzusammenhang beschreiben
Hier sollst du nun ein Ereignis  im Sachzusammenhang beschreiben, dessen Wahrscheinlichkeit durch den folgenden Term berechnet werden kann:
im Sachzusammenhang beschreiben, dessen Wahrscheinlichkeit durch den folgenden Term berechnet werden kann:
 Den Wert des Terms musst du dabei aber nicht berechnen. Du kannst dir dabei zunächst überlegen, was der Term im mathematischen Sinn bedeutet und dies anschließend auf den Sachzusammenhang übertragen.
Den Wert des Terms musst du dabei aber nicht berechnen. Du kannst dir dabei zunächst überlegen, was der Term im mathematischen Sinn bedeutet und dies anschließend auf den Sachzusammenhang übertragen.
Hierfür kannst du den Term in zwei Teile aufteilen und dir zunächst für diese beiden einzelnen Teile klarmachen, was sie bedeuten.


 1. Schritt: Mathematische Bedeutung
Der grüne Teil 1- zeigt dir an, dass es hier um die Berechnung der Wahrscheinlichkeit eines Gegenereignisses geht. Und zwar berechnet
1. Schritt: Mathematische Bedeutung
Der grüne Teil 1- zeigt dir an, dass es hier um die Berechnung der Wahrscheinlichkeit eines Gegenereignisses geht. Und zwar berechnet  die Wahrscheinlichkeit des Gegenereignisses
die Wahrscheinlichkeit des Gegenereignisses  , dessen Wahrscheinlichkeit durch den zweiten (roten) Teil des Terms berechnet wird.
Der rote Teil des Terms hat eine bestimmte Form. Diese Form sollte dir bekannt vorkommen. Sie hat Ähnlichkeiten mit der Formel für die kumulierte Binomialverteilung, die du im vorherigen Aufgabenteil bereits in Form der Tabelle verwendet hast.
Du weißt, dass für eine binomialverteilte Zufallsvariable
, dessen Wahrscheinlichkeit durch den zweiten (roten) Teil des Terms berechnet wird.
Der rote Teil des Terms hat eine bestimmte Form. Diese Form sollte dir bekannt vorkommen. Sie hat Ähnlichkeiten mit der Formel für die kumulierte Binomialverteilung, die du im vorherigen Aufgabenteil bereits in Form der Tabelle verwendet hast.
Du weißt, dass für eine binomialverteilte Zufallsvariable  mit den Parametern
mit den Parametern  und
und  gilt:
gilt:
 Hier beschreibt der Term
Hier beschreibt der Term
 demnach die Wahrscheinlichkeit
demnach die Wahrscheinlichkeit  einer Zufallsvariablen
einer Zufallsvariablen  , die binomialverteilt ist mit den Parametern
, die binomialverteilt ist mit den Parametern  und
und  . Dabei sind
. Dabei sind  und
und  :
:

 Insgesamt ist damit
Insgesamt ist damit  . Diesen Term kannst du mit Hilfe des Gegenereignisses umformulieren und erhältst:
. Diesen Term kannst du mit Hilfe des Gegenereignisses umformulieren und erhältst:
 Damit beschreibt
Damit beschreibt  also die Wahrscheinlichkeit dafür, dass eine binomialverteilte Zufallsvariable
also die Wahrscheinlichkeit dafür, dass eine binomialverteilte Zufallsvariable  mit den Parametern
mit den Parametern  und
und  , mindestens den Wert
, mindestens den Wert  annimmt.
2. Schritt: Übertragung auf den Sachzusammenhang
Dir fällt auf, dass die oben genannte Zufallsvariable
annimmt.
2. Schritt: Übertragung auf den Sachzusammenhang
Dir fällt auf, dass die oben genannte Zufallsvariable  binomialverteilt ist, mit der Wahrscheinlichkeit
binomialverteilt ist, mit der Wahrscheinlichkeit  und dem Stichprobenumfang
und dem Stichprobenumfang  .
.
Im gegebenen Sachzusammenhang beträgt die Wahrscheinlichkeit dafür, dass ein Zuschauer weiblich ist, ebenfalls .
.
Die Zufallsvariable kann also als Zufallsvariable betrachtet werden, die die zufällige Anzahl an weiblichen Zuschauern unter
kann also als Zufallsvariable betrachtet werden, die die zufällige Anzahl an weiblichen Zuschauern unter  Besuchern des untersuchten Bundesliga-Spiels beschreibt.
Damit ist
Besuchern des untersuchten Bundesliga-Spiels beschreibt.
Damit ist  die Wahrscheinlichkeit dafür, dass sich unter den
die Wahrscheinlichkeit dafür, dass sich unter den  zufällig ausgewählten Zuschauern des Bundesliga-Spiels mehr als 300 weibliche Zuschauer befinden.
Demnach beschreibt
zufällig ausgewählten Zuschauern des Bundesliga-Spiels mehr als 300 weibliche Zuschauer befinden.
Demnach beschreibt  das Ereignis, dass sich unter den
das Ereignis, dass sich unter den  zufällig ausgewählten Zuschauern des Bundesliga-Spiels mehr als 300 weibliche Zuschauer befinden.
zufällig ausgewählten Zuschauern des Bundesliga-Spiels mehr als 300 weibliche Zuschauer befinden.
Hierfür kannst du den Term in zwei Teile aufteilen und dir zunächst für diese beiden einzelnen Teile klarmachen, was sie bedeuten.
Im gegebenen Sachzusammenhang beträgt die Wahrscheinlichkeit dafür, dass ein Zuschauer weiblich ist, ebenfalls
Die Zufallsvariable
c) (1)  Ermitteln des zum Erwartungswert symmetrischen Intervalls
Der Aufgabenstellung kannst du jetzt entnehmen, dass bei einem Bundesliga-Spiel 20.000 Zuschauer ins Stadion strömen. An die weiblichen Zuschauer soll dabei ein Flyer verteilt werden, welcher auf ein spezielles Getränkeangebot hinweist.
Deine Aufgabe ist es dabei zunächst, auf Grundlage der 20.000 Zuschauer, das zum Erwartungswert symmetrische Intervall kleinster Länge zu bestimmen, in dem die Anzahl der weiblichen Zuschauer mit einer Wahrscheinlichkeit von mindestens 0,9 bzw. 90 % liegt.
Willst du diese Aufgabe hier lösen, so betrachtest du die Zufallsvariable
Ermitteln des zum Erwartungswert symmetrischen Intervalls
Der Aufgabenstellung kannst du jetzt entnehmen, dass bei einem Bundesliga-Spiel 20.000 Zuschauer ins Stadion strömen. An die weiblichen Zuschauer soll dabei ein Flyer verteilt werden, welcher auf ein spezielles Getränkeangebot hinweist.
Deine Aufgabe ist es dabei zunächst, auf Grundlage der 20.000 Zuschauer, das zum Erwartungswert symmetrische Intervall kleinster Länge zu bestimmen, in dem die Anzahl der weiblichen Zuschauer mit einer Wahrscheinlichkeit von mindestens 0,9 bzw. 90 % liegt.
Willst du diese Aufgabe hier lösen, so betrachtest du die Zufallsvariable  , die die Anzahl der Frauen im Stadion beschreibt. Da sich insgesamt 20.000 Zuschauer im Stadion befinden, gilt für
, die die Anzahl der Frauen im Stadion beschreibt. Da sich insgesamt 20.000 Zuschauer im Stadion befinden, gilt für  :
:  . Weiterhin gilt für die Zufallsvariable
. Weiterhin gilt für die Zufallsvariable  , dass die Wahrscheinlichkeit, für das Befragen einer Frau bei 0,25 bzw. 25 % liegt (siehe Aufgabe zuvor).
Nun sollst du ein 90 %-Konfidenzintervall um den Erwartungswert von
, dass die Wahrscheinlichkeit, für das Befragen einer Frau bei 0,25 bzw. 25 % liegt (siehe Aufgabe zuvor).
Nun sollst du ein 90 %-Konfidenzintervall um den Erwartungswert von  bilden.
Zum Lösen dieser, musst du hier die
bilden.
Zum Lösen dieser, musst du hier die  -Regeln anwenden. Gehe dabei so vor:
-Regeln anwenden. Gehe dabei so vor:
 und
und  ergibt sich
ergibt sich
 .
Damit ist das Laplace-Kriterium für die Zufallsvariable
.
Damit ist das Laplace-Kriterium für die Zufallsvariable  erfüllt und die Sigma-Regeln dürfen angewandt werden.
2. Schritt:
erfüllt und die Sigma-Regeln dürfen angewandt werden.
2. Schritt:  -Regeln umformen
Setze nun wie oben beschrieben in den Ausdruck
-Regeln umformen
Setze nun wie oben beschrieben in den Ausdruck  ein und berechne wie folgt das gesuchte Intervall
ein und berechne wie folgt das gesuchte Intervall
 Das hier gesuchte Intervall ist:
Das hier gesuchte Intervall ist: ![\(\left[4.899;5.101\right]\)](https://mathjax.schullv.de/f783f67e6ca0667e9704b5edaaf0075279cfd88c3cfa8cb894d4cfad3764a85a?color=5a5a5a) .
.
- Berechne zunächst die Standardabweichung von
und stelle mit dieser sicher, ob das Laplace-Kriterium
erfüllt ist.
- Du findest die Regel
- Setze
und
- Forme so weit wie möglich um und ermittle so das gesuchte Intervall.
c) (2)  Voraussetzung, mit der die Wahrscheinlichkeit berechnet werden kann
Der Aufgabenstellung kannst du nun entnehmen, dass sich vor einem Kassenhäuschen eine Schlange von 50 Zuschauern gebildet hat. Deine Aufgabe ist es nun, die Voraussetzung zu nennen, unter der die Wahrscheinlichkeit
Voraussetzung, mit der die Wahrscheinlichkeit berechnet werden kann
Der Aufgabenstellung kannst du nun entnehmen, dass sich vor einem Kassenhäuschen eine Schlange von 50 Zuschauern gebildet hat. Deine Aufgabe ist es nun, die Voraussetzung zu nennen, unter der die Wahrscheinlichkeit  , dass sich in der Schlange 12 weibliche Zuschauer befinden, so berechnet werden kann:
, dass sich in der Schlange 12 weibliche Zuschauer befinden, so berechnet werden kann:
 P= \dbinom{50}{12} \cdot 0,25^{12} \cdot 0,75^{38}
P= \dbinom{50}{12} \cdot 0,25^{12} \cdot 0,75^{38}  Betrachtest du den gegebenen Term genauer, so kannst du erkennen, dass es sich hier um den Ansatz zur Berechnung der Wahrscheinlichkeit einer binomialverteilten Zufallsvariablen handelt. Mit diesem Term können Wahrscheinlichkeiten der Form
Betrachtest du den gegebenen Term genauer, so kannst du erkennen, dass es sich hier um den Ansatz zur Berechnung der Wahrscheinlichkeit einer binomialverteilten Zufallsvariablen handelt. Mit diesem Term können Wahrscheinlichkeiten der Form  für ein bestimmtes
für ein bestimmtes  berechnet werden. Das heißt, die hier gesuchten Voraussetzungen ergeben sich aus den Voraussetzungen für eine binomialverteilte Zufallsvariable.
Damit die Wahrscheinlichkeit hier mit Hilfe der Binomialverteilung berechnet werden kann, muss es sich um ein Ziehen mit Zurücklegen handeln. Das heißt die Wahrscheinlichkeit dafür, dass die Person, die vor dem Kassenhäuschen als nächstes steht, eine Frau ist, muss immer die gleiche sein und darf sich nicht im Laufe des Experiments verändern. Weiterhin darf die hier betrachtete Zufallsvariable nur zwei mögliche Ausprägungen besitzen, es darf also nur zwischen Mann und Frau und nicht z.B. Mann, Frau und Kind unterschieden werden.
berechnet werden. Das heißt, die hier gesuchten Voraussetzungen ergeben sich aus den Voraussetzungen für eine binomialverteilte Zufallsvariable.
Damit die Wahrscheinlichkeit hier mit Hilfe der Binomialverteilung berechnet werden kann, muss es sich um ein Ziehen mit Zurücklegen handeln. Das heißt die Wahrscheinlichkeit dafür, dass die Person, die vor dem Kassenhäuschen als nächstes steht, eine Frau ist, muss immer die gleiche sein und darf sich nicht im Laufe des Experiments verändern. Weiterhin darf die hier betrachtete Zufallsvariable nur zwei mögliche Ausprägungen besitzen, es darf also nur zwischen Mann und Frau und nicht z.B. Mann, Frau und Kind unterschieden werden.
 Entscheiden, ob Berechnung hier zulässig ist
Nun sollst du zusätzlich entscheiden, ob die Berechnung der Wahrscheinlichkeit in der vorliegenden Situation zulässig ist. Stelle dir dazu die Frage, ob die Anzahl der Frauen unter den 50 Personen vor dem Kassenhäuschen als binomialverteilt angenommen werden kann. Dazu musst du dir die Frage stellen, ob es sich hier wirklich um ein Ziehen mit Zurücklegen handelt.
Würde es sich hier nicht um ein Ziehen mit Zurücklegen handeln, so würde sich die Wahrscheinlichkeit für das Auftreten einer Frau unter den 50 Personen vor dem Kassenhäuschen ändern, nachdem eine von ihnen vor dem Kassenhäuschen stand.
Die Wahrscheinlichkeit dafür, dass eine Frau ein deutsches Stadion besucht, liegt laut einer Untersuchung bei 25 %. Diese Wahrscheinlichkeit gilt also für alle Stadien in Deutschland. Die Größe ist also „von außen“ bzw. „exogen“ gegeben. Das heißt, die Wahrscheinlichkeit dafür, dass eine Frau vor dem Kassenhäuschen steht, ist immer die gleiche, weshalb hier ein Ziehen mit Zurücklegen vorliegt und die Berechnung über den gegeben Ansatz zulässig ist.
Entscheiden, ob Berechnung hier zulässig ist
Nun sollst du zusätzlich entscheiden, ob die Berechnung der Wahrscheinlichkeit in der vorliegenden Situation zulässig ist. Stelle dir dazu die Frage, ob die Anzahl der Frauen unter den 50 Personen vor dem Kassenhäuschen als binomialverteilt angenommen werden kann. Dazu musst du dir die Frage stellen, ob es sich hier wirklich um ein Ziehen mit Zurücklegen handelt.
Würde es sich hier nicht um ein Ziehen mit Zurücklegen handeln, so würde sich die Wahrscheinlichkeit für das Auftreten einer Frau unter den 50 Personen vor dem Kassenhäuschen ändern, nachdem eine von ihnen vor dem Kassenhäuschen stand.
Die Wahrscheinlichkeit dafür, dass eine Frau ein deutsches Stadion besucht, liegt laut einer Untersuchung bei 25 %. Diese Wahrscheinlichkeit gilt also für alle Stadien in Deutschland. Die Größe ist also „von außen“ bzw. „exogen“ gegeben. Das heißt, die Wahrscheinlichkeit dafür, dass eine Frau vor dem Kassenhäuschen steht, ist immer die gleiche, weshalb hier ein Ziehen mit Zurücklegen vorliegt und die Berechnung über den gegeben Ansatz zulässig ist.
d)(1)  Gegebene Daten im Baumdiagramm darstellen
Nun ist es deine Aufgabe, die Daten, die du der Aufgabenstellung entnehmen kannst, in das Baumdiagramm einzutragen und die fehlenden relativen Häufigkeiten zu ergänzen.
Dazu kannst du zunächst die Bezeichnungen in die eckigen Kästchen und anschließend die relativen Häufigkeiten in die runden Kästchen eintragen, die du der Aufgabenstellung entnehmen kannst. Anschließend kannst du die fehlenden relativen Häufigkeiten berechnen. Die vier runden Kästchen, die sich jeweils am Ende eines „Astes“, befinden, sind für die Anteile der jeweiligen Gruppe an der Gesamtmitgliederzahl vorgesehen, also beispielsweise, wie groß der Anteil der Frauen im gesamten DFB ist. Die runden Kästchen in der Mitte sind dagegen bedingte relative Häufigkeiten. Hier soll das Feld mit
Gegebene Daten im Baumdiagramm darstellen
Nun ist es deine Aufgabe, die Daten, die du der Aufgabenstellung entnehmen kannst, in das Baumdiagramm einzutragen und die fehlenden relativen Häufigkeiten zu ergänzen.
Dazu kannst du zunächst die Bezeichnungen in die eckigen Kästchen und anschließend die relativen Häufigkeiten in die runden Kästchen eintragen, die du der Aufgabenstellung entnehmen kannst. Anschließend kannst du die fehlenden relativen Häufigkeiten berechnen. Die vier runden Kästchen, die sich jeweils am Ende eines „Astes“, befinden, sind für die Anteile der jeweiligen Gruppe an der Gesamtmitgliederzahl vorgesehen, also beispielsweise, wie groß der Anteil der Frauen im gesamten DFB ist. Die runden Kästchen in der Mitte sind dagegen bedingte relative Häufigkeiten. Hier soll das Feld mit  beispielsweise den Anteil der Mädchen unter allen weiblichen Mitgliedern angeben.
Die Zuschauer werden zunächst in „weiblich“ und „ männlich“ unterschieden. Anschließend werden diese beiden Gruppen jeweils wieder in zwei unterschiedliche Altersgruppen eingeteilt. Bei den weiblichen Zuschauern sind dies „Frauen“ und „Mädchen“, bei den männlichen „Senioren“ und „Junioren“.
Die Bezeichnungen müssen demnach wie folgt eingetragen werden:
beispielsweise den Anteil der Mädchen unter allen weiblichen Mitgliedern angeben.
Die Zuschauer werden zunächst in „weiblich“ und „ männlich“ unterschieden. Anschließend werden diese beiden Gruppen jeweils wieder in zwei unterschiedliche Altersgruppen eingeteilt. Bei den weiblichen Zuschauern sind dies „Frauen“ und „Mädchen“, bei den männlichen „Senioren“ und „Junioren“.
Die Bezeichnungen müssen demnach wie folgt eingetragen werden:
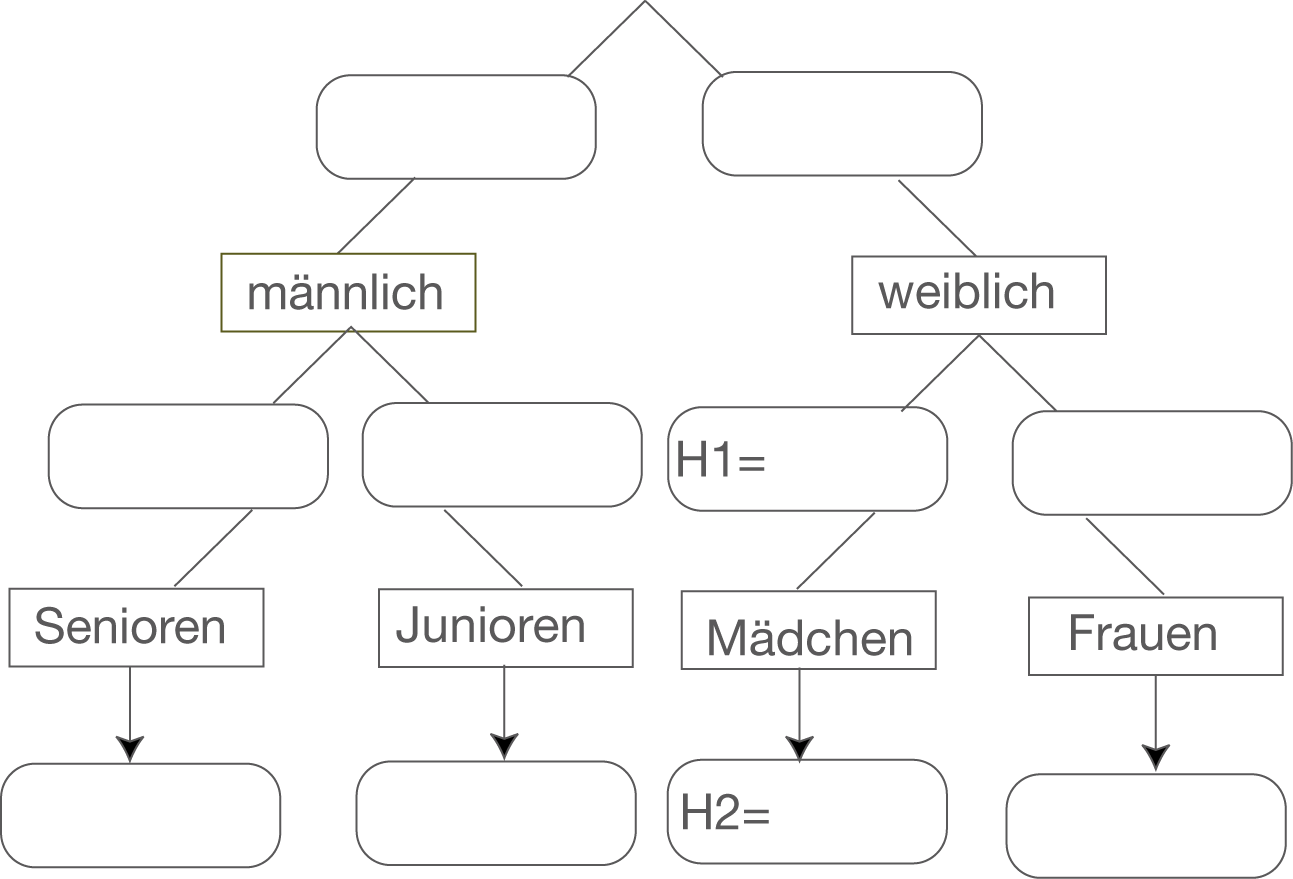 Nun kannst du die relativen Häufigkeiten eintragen, die du der Aufgabenstellung bereits entnehmen kannst. Damit ergibt sich dann das folgende Diagramm:
Nun kannst du die relativen Häufigkeiten eintragen, die du der Aufgabenstellung bereits entnehmen kannst. Damit ergibt sich dann das folgende Diagramm:
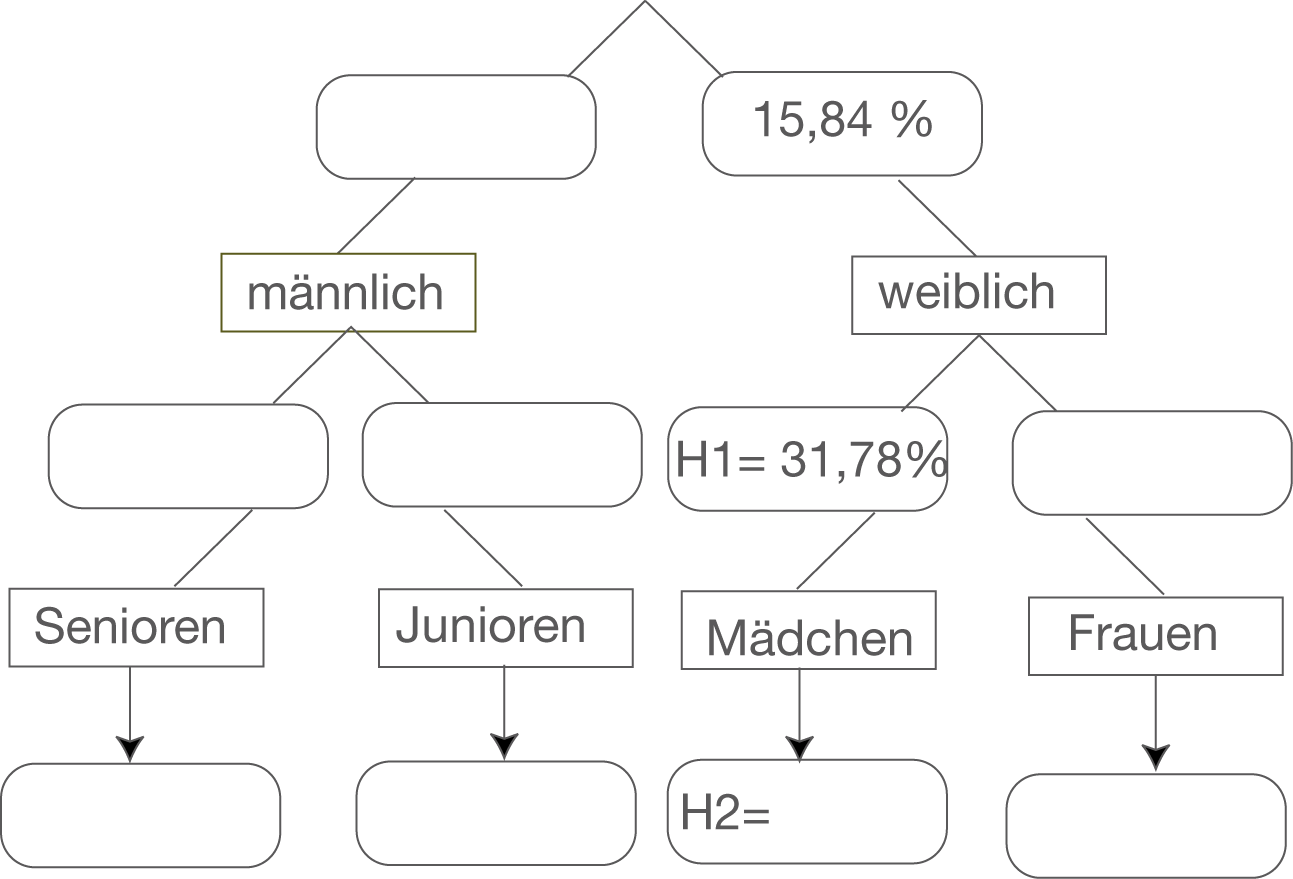 Nun kannst du die fehlenden relativen Häufigkeiten berechnen.
Da ein Mitglied entweder weiblich oder männlich ist, weder beides noch keins von beidem sein kann, muss der Anteil
Nun kannst du die fehlenden relativen Häufigkeiten berechnen.
Da ein Mitglied entweder weiblich oder männlich ist, weder beides noch keins von beidem sein kann, muss der Anteil  der männlichen Mitglieder zusammen mit dem Anteil
der männlichen Mitglieder zusammen mit dem Anteil  der weiblichen Mitglieder
der weiblichen Mitglieder  ergeben. Dadurch erhältst du für den Anteil der männlichen Mitglieder:
ergeben. Dadurch erhältst du für den Anteil der männlichen Mitglieder:
 .
Genauso kannst du auch bei dem Anteil
.
Genauso kannst du auch bei dem Anteil  der Frauen an der Zahl der weiblichen Mitglieder vorgehen, da ein weibliches Mitglied entweder der Altersgruppe der Frauen oder der Altersgruppe der Mädchen angehören muss. Dann erhältst du:
der Frauen an der Zahl der weiblichen Mitglieder vorgehen, da ein weibliches Mitglied entweder der Altersgruppe der Frauen oder der Altersgruppe der Mädchen angehören muss. Dann erhältst du:
 .
Trägst du diese relativen Häufigkeiten ebenfalls ein, so erhältst du folgendes Diagramm:
.
Trägst du diese relativen Häufigkeiten ebenfalls ein, so erhältst du folgendes Diagramm:
 Nun kannst du noch den Anteil
Nun kannst du noch den Anteil  der Frauen an der Gesamtmitgliederzahl berechnen. Dieser ergibt sich mit Hilfe der Pfadmultiplikationsregel durch den Anteil der weiblichen Mitglieder multipliziert mit dem Anteil der Frauen an der Zahl der weiblichen Mitglieder:
der Frauen an der Gesamtmitgliederzahl berechnen. Dieser ergibt sich mit Hilfe der Pfadmultiplikationsregel durch den Anteil der weiblichen Mitglieder multipliziert mit dem Anteil der Frauen an der Zahl der weiblichen Mitglieder:
 .
Genauso kannst du auch den Anteil
.
Genauso kannst du auch den Anteil  der Mädchen an der Gesamtmitgliederzahl berechnen und erhältst:
der Mädchen an der Gesamtmitgliederzahl berechnen und erhältst:
 .
Nun weißt du noch, dass insgesamt ca.
.
Nun weißt du noch, dass insgesamt ca.  der Mitglieder zu den Jugendlichen gehören. Der Anteil der Junioren an der Gesamtmitgliederzahl und der Anteil der Mädchen an der Gesamtmitgliederzahl müssen also zusammen
der Mitglieder zu den Jugendlichen gehören. Der Anteil der Junioren an der Gesamtmitgliederzahl und der Anteil der Mädchen an der Gesamtmitgliederzahl müssen also zusammen  betragen. Damit ergibt sich für den Anteil der Junioren an der Mitgliederzahl:
betragen. Damit ergibt sich für den Anteil der Junioren an der Mitgliederzahl:  .
Als nächstes bietet es sich an, den Anteil
.
Als nächstes bietet es sich an, den Anteil  zu berechnen. Dieser ergibt sich wieder mit Hilfe der Pfadmultiplikationsregel. Es muss gelten:
zu berechnen. Dieser ergibt sich wieder mit Hilfe der Pfadmultiplikationsregel. Es muss gelten:
 .
Setzt du dort die relativen Häufigkeiten ein, die du bereits bestimmt hast, so ergibt sich eine Gleichung, die du nach
.
Setzt du dort die relativen Häufigkeiten ein, die du bereits bestimmt hast, so ergibt sich eine Gleichung, die du nach  lösen kannst:
lösen kannst:
 Trägst du diese berechneten relativen Häufigkeiten in dein Diagramm ein, so sollte es ähnlich aussehen wie hier:
Trägst du diese berechneten relativen Häufigkeiten in dein Diagramm ein, so sollte es ähnlich aussehen wie hier:
 Nun kannst du wie zuvor die beiden übrigen relativen Häufigkeiten berechnen:
Nun kannst du wie zuvor die beiden übrigen relativen Häufigkeiten berechnen:
 .
.
 .
Damit ist das Baumdiagramm nun gefüllt und sollte so aussehen:
.
Damit ist das Baumdiagramm nun gefüllt und sollte so aussehen:
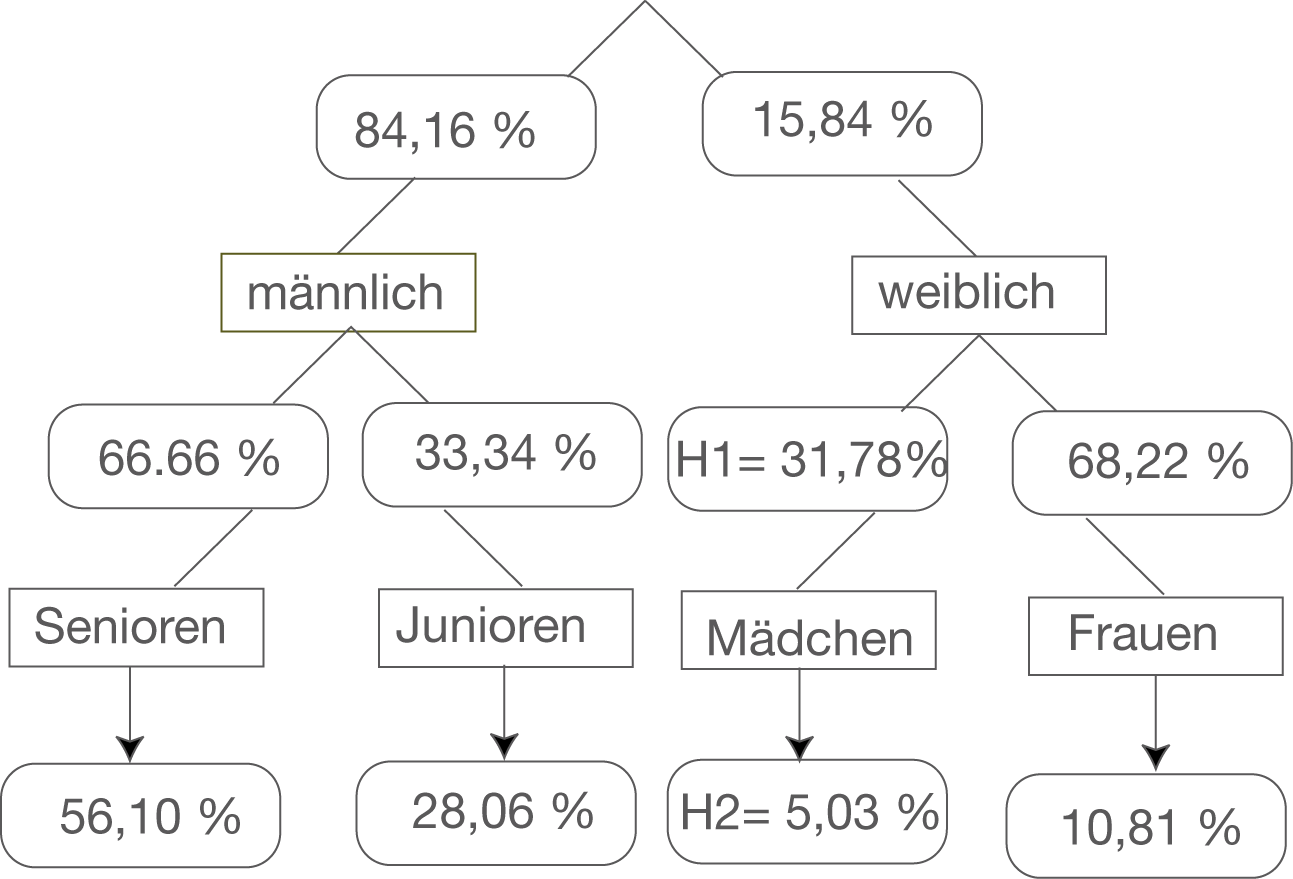 d) (2)
d) (2)  Relative Häufigkeiten beschreiben
Nun sollst du die beiden relativen Häufigkeiten, die im Baumdiagramm mit
Relative Häufigkeiten beschreiben
Nun sollst du die beiden relativen Häufigkeiten, die im Baumdiagramm mit  und
und  gekennzeichnet sind, mit Worten beschreiben.
gekennzeichnet sind, mit Worten beschreiben.
 gibt den Anteil der Mädchen an, den diese an der Gesamtzahl der weiblichen Mitglieder haben. Also gehören
gibt den Anteil der Mädchen an, den diese an der Gesamtzahl der weiblichen Mitglieder haben. Also gehören  aller weiblichen Mitglieder zur Altersgruppe der Mädchen.
aller weiblichen Mitglieder zur Altersgruppe der Mädchen.
 gibt den Anteil der Mädchen an, den diese an der Gesamtmitgliederzahl haben. Dies bedeutet, dass
gibt den Anteil der Mädchen an, den diese an der Gesamtmitgliederzahl haben. Dies bedeutet, dass  aller Mitglieder des DFB Mädchen sind.
d) (3)
aller Mitglieder des DFB Mädchen sind.
d) (3)  Ermitteln der Wahrscheinlichkeiten
Nun werden zwei Mitglieder des DFB zufällig ausgewählt und du sollst die Wahrscheinlichkeit dafür ermitteln, dass es sich bei den beiden Personen
Ermitteln der Wahrscheinlichkeiten
Nun werden zwei Mitglieder des DFB zufällig ausgewählt und du sollst die Wahrscheinlichkeit dafür ermitteln, dass es sich bei den beiden Personen
 Die Wahrscheinlichkeit dafür, einen „Junior“ und ein „Mädchen“ auszuwählen liegt also bei 0,0282 bzw. 2,82 %.
Die Wahrscheinlichkeit dafür, einen „Junior“ und ein „Mädchen“ auszuwählen liegt also bei 0,0282 bzw. 2,82 %.





- um einen „Junior“
- und ein „Mädchen“ handelt.
- Wahrscheinlichkeit für einen „Junior“:
- Wahrscheinlichkeit für ein „Mädchen“:
e)(1)  Wahl der Nullhypothese begründen
Der Verkaufsleiter führt einen Hypothesentest durch um zu überprüfen, ob der Anteil der weiblichen Stadionbesucher tatsächlich gestiegen ist. Ist dies der Fall, so stellt er mehr Vorräte für die speziellen Angebote für die weiblichen Besucher bereit. Du sollst nun die Wahl seiner Nullhypothese
Wahl der Nullhypothese begründen
Der Verkaufsleiter führt einen Hypothesentest durch um zu überprüfen, ob der Anteil der weiblichen Stadionbesucher tatsächlich gestiegen ist. Ist dies der Fall, so stellt er mehr Vorräte für die speziellen Angebote für die weiblichen Besucher bereit. Du sollst nun die Wahl seiner Nullhypothese  begründen.
Der Aufgabenstellung kannst du entnehmen, dass er möglichst nicht zu viele Vorräte für die speziellen Angebote einkaufen möchte. Ausgehend von dieser Information kannst du nun überlegen, warum es deshalb sinnvoll ist, die Nullhypothese so zu wählen.
Der Verkaufsleiter möchte unbedingt verhindern zu viele Vorräte für die speziellen Angebote zu kaufen und dadurch auf verderblicher Ware sitzen zu bleiben. Er wird also nur davon ausgehen, dass der Anteil der weiblichen Zuschauer tatsächlich auf mehr als
begründen.
Der Aufgabenstellung kannst du entnehmen, dass er möglichst nicht zu viele Vorräte für die speziellen Angebote einkaufen möchte. Ausgehend von dieser Information kannst du nun überlegen, warum es deshalb sinnvoll ist, die Nullhypothese so zu wählen.
Der Verkaufsleiter möchte unbedingt verhindern zu viele Vorräte für die speziellen Angebote zu kaufen und dadurch auf verderblicher Ware sitzen zu bleiben. Er wird also nur davon ausgehen, dass der Anteil der weiblichen Zuschauer tatsächlich auf mehr als  gestiegen ist und dementsprechend mehr Vorräte einkaufen, wenn deutlich mehr weibliche Besucher als erwartet in der Stichprobe gezählt werden. Weil er auf Nummer sicher gehen will, wählt er daher die Nullhypothese
gestiegen ist und dementsprechend mehr Vorräte einkaufen, wenn deutlich mehr weibliche Besucher als erwartet in der Stichprobe gezählt werden. Weil er auf Nummer sicher gehen will, wählt er daher die Nullhypothese  .
.
 Entscheidungsregel ermitteln
Nun sollst du eine Entscheidungsregel ermitteln. Du sollst also auf Grundlage einer Irrtumswahrscheinlichkeit von
Entscheidungsregel ermitteln
Nun sollst du eine Entscheidungsregel ermitteln. Du sollst also auf Grundlage einer Irrtumswahrscheinlichkeit von  ein Intervall bestimmen, sodass der Verkaufsleiter seine Nullhypothese bestätigt sieht, wenn die Anzahl der weiblichen Zuschauer innerhalb dieses Intervalls liegt. Andernfalls wird die Nullhypothese abgelehnt. Die Wahl der Null- und Gegenhypothese ist dir bereits gegeben. Daraus kannst du schließen, dass hier ein rechtsseitiger Hypothesentest durchgeführt wird. Der Annahmebereich hat damit folgende Form:
ein Intervall bestimmen, sodass der Verkaufsleiter seine Nullhypothese bestätigt sieht, wenn die Anzahl der weiblichen Zuschauer innerhalb dieses Intervalls liegt. Andernfalls wird die Nullhypothese abgelehnt. Die Wahl der Null- und Gegenhypothese ist dir bereits gegeben. Daraus kannst du schließen, dass hier ein rechtsseitiger Hypothesentest durchgeführt wird. Der Annahmebereich hat damit folgende Form:
Der Ablehungsbereich hat dementsprechend die Form:
Um eine Entscheidungsregel formulieren zu können, benötigst du also die rechte Grenze des Annahmebereichs, den Wert  . Um diesen zu berechnen, können dir die
. Um diesen zu berechnen, können dir die  -Regeln helfen. Gehe also so vor:
-Regeln helfen. Gehe also so vor:
 welche die Anzahl der weiblichen Zuschauer in der gegebenen Stichprobe vom Umfang 1.000 beschreibt. Die Zufallsvariable
welche die Anzahl der weiblichen Zuschauer in der gegebenen Stichprobe vom Umfang 1.000 beschreibt. Die Zufallsvariable  ist hier wieder mit
ist hier wieder mit  und
und  mit der gleichen Begründung wie in den Aufgabenteilen zuvor binomialverteilt.
2. Schritt: Annahme- und Ablehnungsbereich bestimmen
Um die
mit der gleichen Begründung wie in den Aufgabenteilen zuvor binomialverteilt.
2. Schritt: Annahme- und Ablehnungsbereich bestimmen
Um die  -Regeln anwenden zu können, muss
-Regeln anwenden zu können, muss  gelten. Diesen Wert kannst du mit Hilfe folgender Formel berechnen, die du auch im Anhang mit den
gelten. Diesen Wert kannst du mit Hilfe folgender Formel berechnen, die du auch im Anhang mit den  -Regeln des Aufgabenblattes findest:
-Regeln des Aufgabenblattes findest:
Setzt du dort die entsprechenden Werte  und
und  ein, so erhältst du:
ein, so erhältst du:
 Du kannst hier also die
Du kannst hier also die  -Regeln anwenden.
Passende
-Regeln anwenden.
Passende  -Regel auswählen
Die passende Regel findest du mit Hilfe der Irrtumswahrscheinlichkeit. Diese ist dir mit
-Regel auswählen
Die passende Regel findest du mit Hilfe der Irrtumswahrscheinlichkeit. Diese ist dir mit  gegeben. Da hier ein rechtsseitiger Test durchgeführt wird, soll gelten:
gegeben. Da hier ein rechtsseitiger Test durchgeführt wird, soll gelten:
 also
also  .
Dies kannst du mit Hilfe des Gegenereignisses umformulieren und erhältst:
.
Dies kannst du mit Hilfe des Gegenereignisses umformulieren und erhältst:
 Damit findest du die folgende
Damit findest du die folgende  -Regel:
-Regel:
Grenze  berechnen
Es muss also gelten:
berechnen
Es muss also gelten:  . Den Wert für
. Den Wert für  kennst du bereits. Berechne nun noch
kennst du bereits. Berechne nun noch  mit Hilfe der folgenden Formel:
mit Hilfe der folgenden Formel:
 Damit kannst du nun
Damit kannst du nun  berechnen und erhältst:
berechnen und erhältst:
 Da ein Annahmebereich nur aus ganzzahligen Werten besteht (es kann schließlich keine halben Besucher geben), muss hier gerundet werden. Weil das
Da ein Annahmebereich nur aus ganzzahligen Werten besteht (es kann schließlich keine halben Besucher geben), muss hier gerundet werden. Weil das  der kleinste Wert ist, für den
der kleinste Wert ist, für den  gerade noch
gerade noch  ist, muss hier aufgerundet werden:
ist, muss hier aufgerundet werden:  .
Damit lauten der Annahmebereich und der Ablehnungsbereich wie folgt:
.
Damit lauten der Annahmebereich und der Ablehnungsbereich wie folgt:
![\(A = [0,..,273]\)](https://mathjax.schullv.de/dc3868078bd327c26b2d3e38320e9e0f6f2c34974a205527629d2e639f236b03?color=5a5a5a) und
und ![\(\overline{A} = [274,...,1.000]\)](https://mathjax.schullv.de/c734ef3d60512448aa0bfa1919a3663e8eeff32322b925e9b1c68b4e0c750ea3?color=5a5a5a) 3. Schritt: Entscheidungsregel formulieren
Du weißt, dass der Verkaufsleiter die Nullhypothese ablehnt, wenn
3. Schritt: Entscheidungsregel formulieren
Du weißt, dass der Verkaufsleiter die Nullhypothese ablehnt, wenn  einen Wert aus dem Ablehnungsbereich annimmt. In diesem Fall würde er mehr Vorräte einkaufen, weil er davon ausginge, dass der Anteil der weiblichen Besucher tatsächlich höher als
einen Wert aus dem Ablehnungsbereich annimmt. In diesem Fall würde er mehr Vorräte einkaufen, weil er davon ausginge, dass der Anteil der weiblichen Besucher tatsächlich höher als  ist.
Werden unter den
ist.
Werden unter den  zufällig ausgewählten Fotos mehr als
zufällig ausgewählten Fotos mehr als  weibliche Stadionbesucher gefunden, so lehnt der Verkaufsleiter seine Nullhypothese unter dem Signifikanzniveau
weibliche Stadionbesucher gefunden, so lehnt der Verkaufsleiter seine Nullhypothese unter dem Signifikanzniveau  ab und geht von einem Anteil an weiblichen Personen aus, der höher als
ab und geht von einem Anteil an weiblichen Personen aus, der höher als  ist. In diesem Fall kauft er mehr Vorräte für die speziellen Angebote für Frauen ein.
Werden in der Stichprobe
ist. In diesem Fall kauft er mehr Vorräte für die speziellen Angebote für Frauen ein.
Werden in der Stichprobe  oder weniger Fotos von Frauen gefunden, so geht der Verkaufsleiter bei einer Irrtumswahrscheinlichkeit von
oder weniger Fotos von Frauen gefunden, so geht der Verkaufsleiter bei einer Irrtumswahrscheinlichkeit von  davon aus, dass der Anteil weiblicher Besucher nicht gestiegen ist und immer noch maximal bei
davon aus, dass der Anteil weiblicher Besucher nicht gestiegen ist und immer noch maximal bei  liegt. In diesem Fall kauft der Verkaufsleiter nicht mehr Vorräte als sonst üblich ein.
e) (2)
liegt. In diesem Fall kauft der Verkaufsleiter nicht mehr Vorräte als sonst üblich ein.
e) (2)  Beschreiben des Fehlers 2. Art und Berechnen der Wahrscheinlichkeit
Hier sollst du nun zum obigen Hypothesentest den Fehler 2. Art beschreiben und die Wahrscheinlichkeit für diesen berechnen, für den Fall, dass der Anteil der weiblichen Zuschauer tatsächlich 30 % beträgt.
Beschreiben des Fehlers 2. Art und Berechnen der Wahrscheinlichkeit
Hier sollst du nun zum obigen Hypothesentest den Fehler 2. Art beschreiben und die Wahrscheinlichkeit für diesen berechnen, für den Fall, dass der Anteil der weiblichen Zuschauer tatsächlich 30 % beträgt.
Der Fehler 2. Art beschreibt immer ein Ablehnen der Gegenhypothese, obwohl diese wahr ist. Hier bedeutet das ein Ablehnen der Gegenhypothese obwohl eigentlich
obwohl eigentlich  gilt. Im Sachzusammenhang interpretiert bedeutet das, dass der Anteil der weiblichen Zuschauer in Wirklichkeit über 25 % gestiegen ist, obwohl dies mit dem Hypothesentest widerlegt wurde.
gilt. Im Sachzusammenhang interpretiert bedeutet das, dass der Anteil der weiblichen Zuschauer in Wirklichkeit über 25 % gestiegen ist, obwohl dies mit dem Hypothesentest widerlegt wurde.
Betrachtest du dazu Zufallsvariable die mit
die mit  und
und  die Anzahl der weiblichen Stadionbesucher nach gestiegenem Anteil beschreibt, dann nimmt diese einen Wert aus dem Annahmebereich für die Nullhypothese an, wenn der Fehler 2. Art eintritt.
Willst du die Wahrscheinlichkeit hier berechnen, so musst du also folgenden Term betrachten:
die Anzahl der weiblichen Stadionbesucher nach gestiegenem Anteil beschreibt, dann nimmt diese einen Wert aus dem Annahmebereich für die Nullhypothese an, wenn der Fehler 2. Art eintritt.
Willst du die Wahrscheinlichkeit hier berechnen, so musst du also folgenden Term betrachten:
Verwende dazu auch hier wieder die Tabelle zur kumulierten Binomialverteilung ( ) oder deinen GTR.
) oder deinen GTR.
 Lösungsweg A: Tabelle zur kumulierten Binomialverteilung
Betrachte hier die Tabelle für
Lösungsweg A: Tabelle zur kumulierten Binomialverteilung
Betrachte hier die Tabelle für  und
und  und suche den Wert an der Stelle
und suche den Wert an der Stelle  .
.
Für die Wahrscheinlichkeit ergibt sich also: .
.
 Lösungsweg B: Lösung über GTR
Verwende hier wieder wie in den Aufgabenteilen zuvor deinen GTR. Mit dem Bcd-Befehl ergibt sich hier:
Lösungsweg B: Lösung über GTR
Verwende hier wieder wie in den Aufgabenteilen zuvor deinen GTR. Mit dem Bcd-Befehl ergibt sich hier:
 Die Wahrscheinlichkeit für den Fehler 2. Art ist hier also 0,329 bzw. 3,29 %.
Die Wahrscheinlichkeit für den Fehler 2. Art ist hier also 0,329 bzw. 3,29 %.
|
|
|
|
- Führe eine Zufallsvariable
für die Anzahl der weiblichen Zuschauer ein.
- Bestimme den Annahme- und Ablehnungsbereich, indem du die
-Regeln anwendest. Berechne dazu zunächst
um zu überprüfen, ob das Laplace-Kriterium erfüllt ist. Wähle dann die hier passende
-Regel aus und berechne anschließend
. Danach kannst du die Grenzen des Annahme- und Ablehnungsbereichs berechnen.
- Formuliere eine Entscheidungsregel
|
|
|
|
|
{ |
Der Fehler 2. Art beschreibt immer ein Ablehnen der Gegenhypothese, obwohl diese wahr ist. Hier bedeutet das ein Ablehnen der Gegenhypothese
Betrachtest du dazu Zufallsvariable
|
|
Für die Wahrscheinlichkeit ergibt sich also:
