Aufgabe 1

Gegeben ist die Funktion $f$ mit der Gleichung $f(x)=9\cdot x\cdot \mathbb{e}^{-1,5\cdot x},$ $x\in\mathbb{R}.$ Der Graph der Funktion $f$ ist in Abbildung 1 dargestellt.

Für die zweite Ableitung der Funktion $f$ gilt: $\(f$

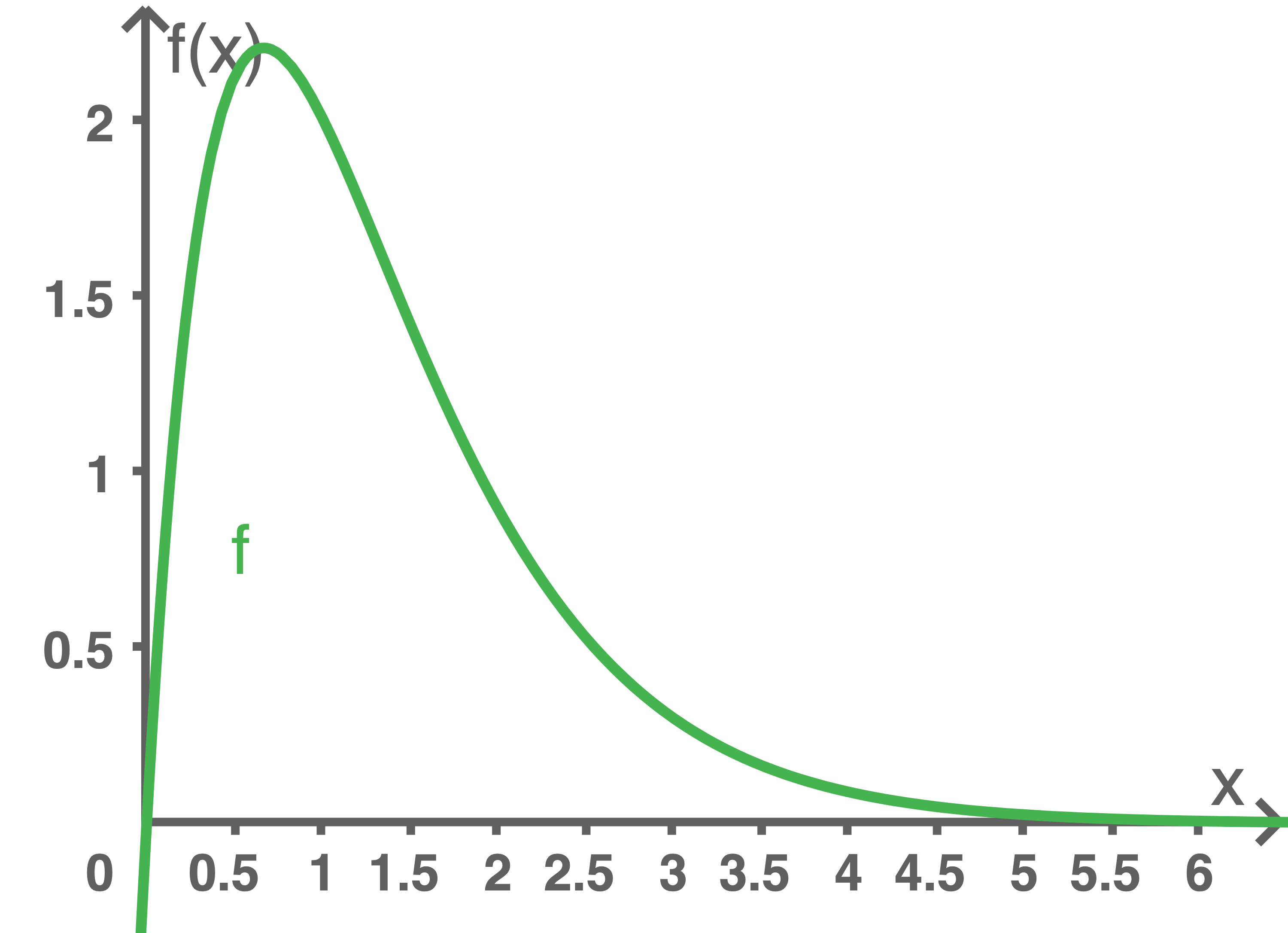
nrw abi gk gtr 2022 teil b aufgabe 1 abbildung 2 funktion f

Abbildung 1

(1)

Begründe, dass die Funktion $f$ nur eine Nullstelle besitzt.

(2)

Zeige, dass $\(f$ die erste Ableitung der Funktion $f$ ist.

(3)

Untersuche den Graphen von $f$ rechnerisch auf lokale Extrempunkte.

(4)

Der Graph der Funktion $f$ hat genau einen Wendepunkt.
Ermittle die Koordinaten des Wendepunktes.

(5)

Ermittle, an welchen Stellen im Intervall $[0;6]$ der Graph der Funktion $f$ die größte bzw. kleinste Steigung hat.

(2 + 2 + 4 + 2 + 3 Punkte)

Der Graph der Funktion $f,$ die $x$ -Achse und die Gerade mit der Gleichung $x=6$ schließen die Fläche $A$ ein.

(1)

Ermittle den Inhalt der Fläche $A.$

(2)

Für jedes $0\lt u\leq6$ sind $O(0\mid0),$ $P(6\mid0)$ und $Q_u(u\mid f(u))$ die Eckpunkte eines Dreiecks.

(i)

Zeichne das Dreieck $OPQ_u$ mit $u=2$ in Abbildung 1 ein.

(ii)

Begründe, dass sich der Flächeninhalt des Dreiecks $OPQ_u$ in Abhängigkeit von $u$ mit der Gleichung $A_{OPQ_u}(u)=3\cdot f(u)$ berechnen lässt.

(iii)

Begründe ohne weitere Rechnung, für welchen Wert von $u$ der Flächeninhalt des Dreiecks $OPQ_u$ maximal wird.

(iv)

Bestimme alle Werte von $u,$ für die das Dreieck $OPQ_u$ einen Flächeninhalt von $4$ Flächeneinheiten hat.

(2 + 7 Punkte)

Für ein $z$ mit $\dfrac{2}{3}\lt z\lt\dfrac{4}{3}$ ist der Punkt $R(z\mid f(z))$ gegeben. Der Graph der Funktion $t$ ist die Tangente an den Graphen von $f$ im Punkt $R.$ Für $x\lt z$ wird der Graph von $f$ betrachtet. Für $x\geq z$ wird der Graph von $t$ betrachtet. Abbildung 2 veranschaulicht diese Situation für das Beispiel $z = 0,9.$
Die betrachteten Graphen der Funktionen $f$ und $t$ schließen mit der $x$ -Achse die in Abbildung 2 farbig dargestellte Fläche ein. Der Wert von $z$ kann mithilfe der folgenden Bedingungen so bestimmt werden, dass diese Fläche einen Flächeninhalt von $4$ Flächeneinheiten hat:

$I:$

$t(z)=f(z)$

$II:$

$\(t$

$III:$

$\displaystyle\int_{0}^{z}f(x)\;\mathrm dx+\displaystyle\int_{z}^{c}t(x)\;\mathrm dx=4,$ wobei $c$ die Nullstelle von $t$ ist.

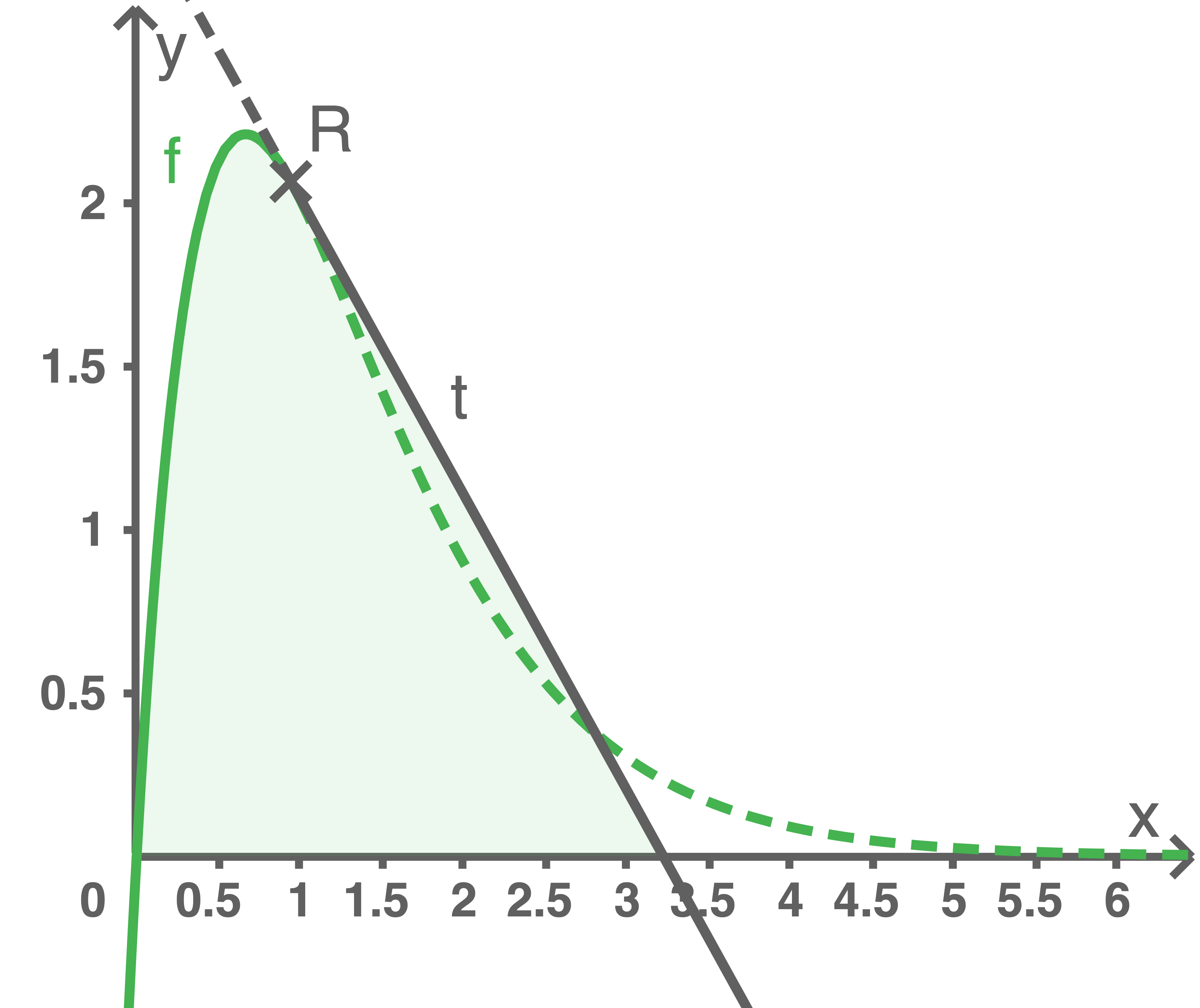
nrw abi gk gtr 2022 teil b aufgabe 1 abbildung 3 funktion f tangente t punkt r

Abbildung 2

(1)

(i)

Begründe die Wahl der Bedingungen $I$ und $II.$

(ii)

Erläutere die linke Seite der Gleichung in Bedingung $III.$

(2)

Aus den Bedingungen folgt $z\approx0,9428.$ [Nachweis nicht erforderlich.]

Bestimme für $z = 0,9428$ rechnerisch eine Gleichung der Funktion $t ,$ deren Graph die Tangente an den Graphen von $f$ im Punkt $R(z\mid f(z))$ ist.

(4 + 3 Punkte)

Für $k\gt0$ ist die Funktion $j$ mit der Gleichung $j(x)=4\cdot k^2\cdot x\cdot \mathbb{e}^{-k\cdot x}$ für $x\in\mathbb{R}$ gegeben. Setzt man $k=1,5$ in den Funktionsterm von $j$ ein, so erhält man den Funktionsterm von $f.$
Setzt man $k=2,6$ in den Funktionsterm von $j$ ein, so erhält man den Funktionsterm der Funktion $g$ mit $g(x)=4\cdot 2,6^2\cdot x\cdot \mathbb{e}^{-2,6\cdot x}.$

(1)

Die Graphen der Funktionen $f$ und $g$ schneiden sich nur im Koordinatenursprung und in einem weiteren Punkt $S.$

(i)

Bestimme die Koordinaten des Hochpunkts des Graphen von $g$ und des Schnittpunkts $S$ der Graphen von $f$ und $g.$

(ii)

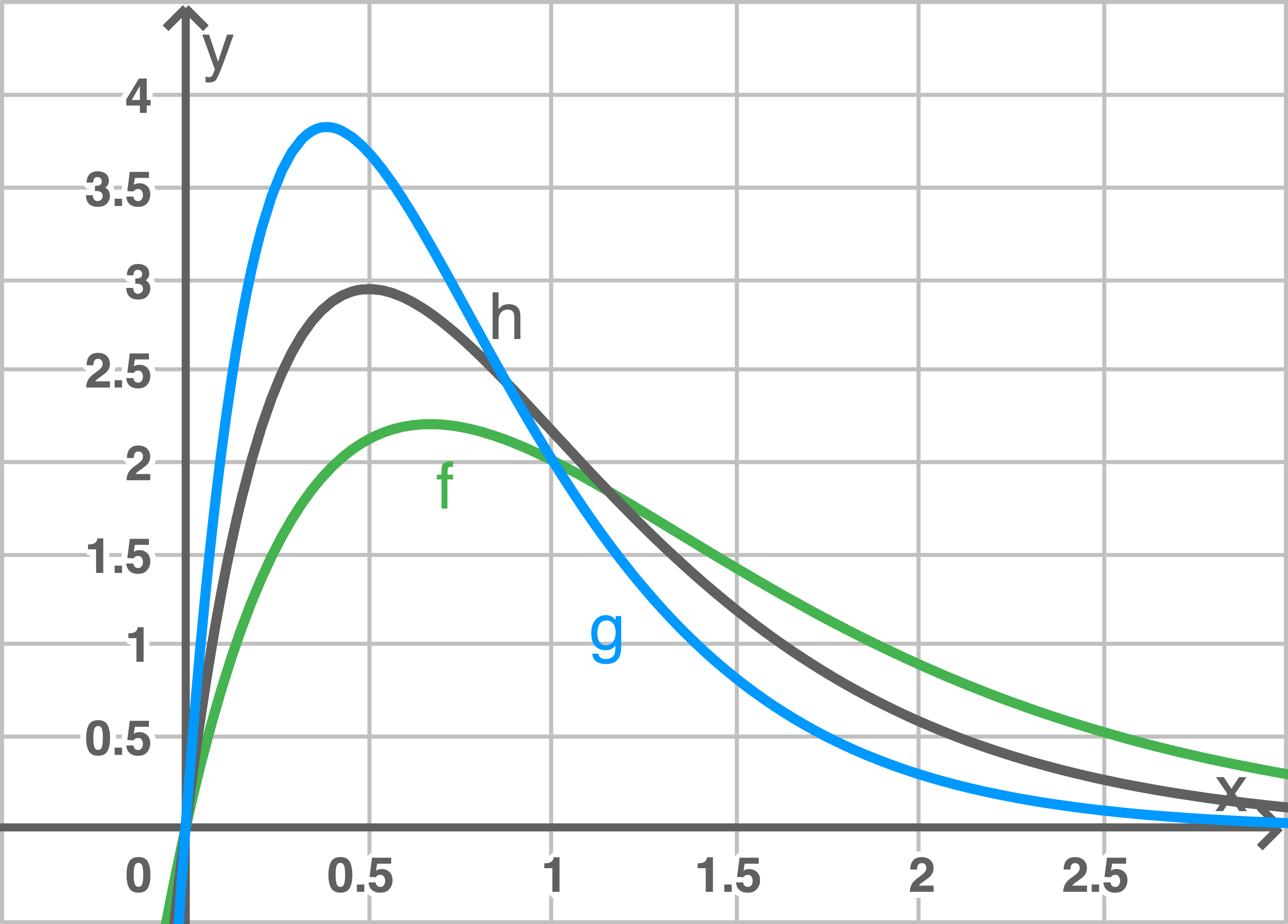
Skizziere mithilfe dieser Punkte den Graphen der Funktion $g$ in Abbildung 3.

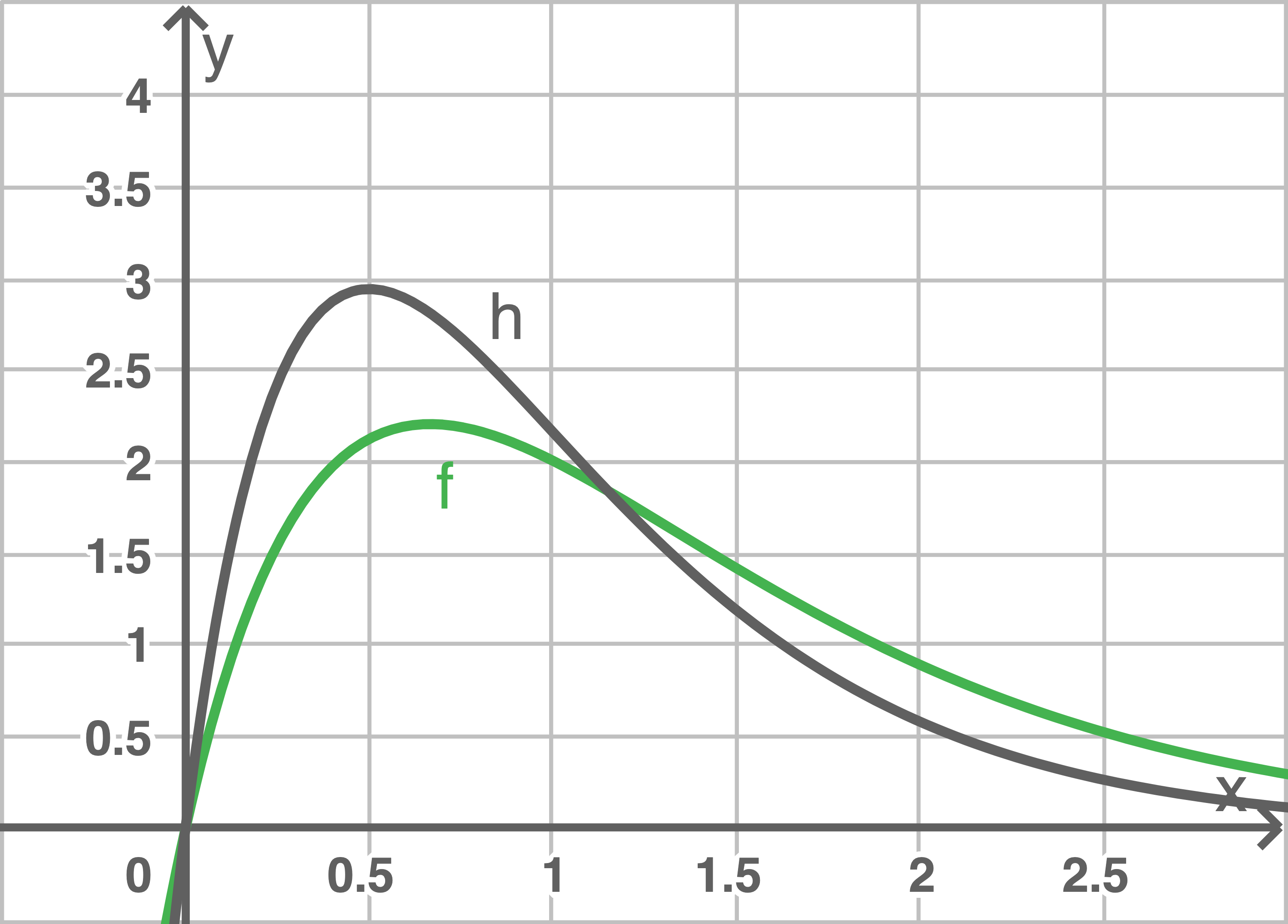
Abbildung 3

(2)

Setzt man einen bestimmten Wert von $k$ in den Funktionsterm von $j$ ein, so erhält man den Funktionsterm der Funktion $h,$ deren Graph in Abbildung 3 dargestellt ist.
Gib ohne weitere Rechnung einen Schätzwert für diesen Wert von $k$ an.

(5 + 1 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

(1)

$\begin{array}[t]{rll} f(x)&=& 0 \\[5pt] 9\cdot x \cdot \mathrm e^{-1,5\cdot x}&=& 0 &\quad \scriptsize \mid\; :9 \\[5pt] x \cdot \mathrm e^{-1,5\cdot x}&=& 0 \end{array}$

Mit dem Satz vom Nullprodukt folgt:

Da $\mathrm e^{-1,5\cdot x}\neq 0$ gilt:

$x=0.$

(2)

Mit der Produktregel gilt:

$\(\begin{array}[t]{rll} f$

(3)

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

Mit dem Satz vom Nullprodukt und $\mathrm e^{-1,5\cdot x}\neq0$ gilt:

$\begin{array}[t]{rll} -\dfrac{27}{2}x+9 &=& 0 &\quad \scriptsize \mid\; -9 \\[5pt] -\dfrac{27}{2}x &=& -9 &\quad \scriptsize \mid\; :(-\dfrac{27}{2}) \\[5pt] x &=& \dfrac{2}{3} \end{array}$

2. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$\(f$

Somit befindet sich an der Stelle $x=\dfrac{2}{3}$ der Hochpunkt des Graphen der Funktion $f$ .

3. Schritt: Extremstellen in $f(x)$ einsetzen

$f\left( \dfrac{2}{3} \right)=\dfrac{6}{\mathrm e}$

Der Graph der Funktion $f$ hat den Hochpunkt $H\left( \dfrac{2}{3}\,\bigg \vert \, \dfrac{6}{\mathrm e} \right).$

(4)

Es muss $\(f$ gelten.

Mit dem GTR wird die Extremstelle des Graphen der Ableitungsfunktion f' bestimmt.

$x_w=\dfrac{4}{3}.$

$f\left( \dfrac{4}{3} \right)=\dfrac{12}{\mathrm e^2}$

Der Graph der Funktion $f$ hat den Wendepunkt $W\left(\dfrac{4}{3}\,\bigg \vert \,\dfrac{12}{\mathrm e^2}\right).$

(5)

Die größte bzw. kleinste Steigung liegt im Wendepunkt oder am Rand des Intervalls vor. Es gilt: $\(f$ , $\(f$ und $\(f$ . Die Steigung ist an der Stelle $x = 0$ am größten und an der Wendestelle $x \approx 1,33$ am kleinsten.

(1)

$\begin{array}[t]{rll} A&=& \displaystyle\int_{0}^{6}f(x)\;\mathrm dx \\[5pt] &=& \displaystyle\int_{0}^{6} 9\cdot x \cdot \mathrm e^{-1,5\cdot x} \;\mathrm dx \\[5pt] &=&A=4 \; \text{[FE]} \end{array}$

(2)

(i)

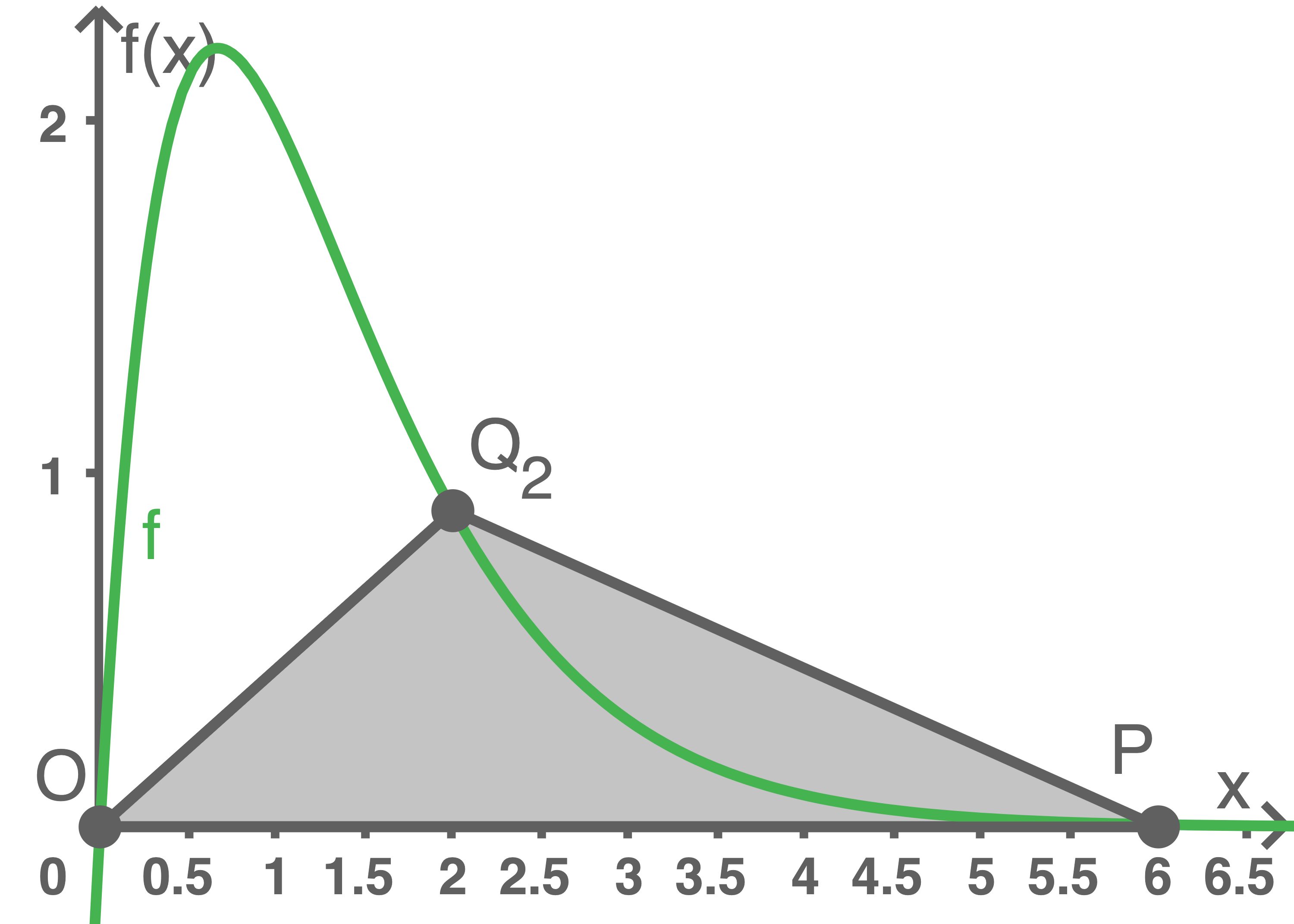
(ii)

Da die Grundseite $\overline{OP}$ des Dreiecks $OPQ_u$ eine Länge von $6\;\text{LE}$ hat und die Länge der zugehörigen Höhe durch $f(u)$ gegeben ist, gilt für den Flächeninhalt des Dreiecks:

$A_{OPQ_u}(u)=\dfrac{1}{2}\cdot 6 \cdot f(u)=3\cdot f(u).$

(iii)

Da der Flächeninhalt immer der dreifache Wert des Funktionswertes $f(u)$ und der Funktionswert im Hochpunkt maximal ist, wird der Flächeninhalt des Dreiecks $OPQ_u$ für $u=\dfrac{2}{3}$ maximal.

(iv)

$\begin{array}[t]{rll} A_{OPQ_u}&=& 4 \\[5pt] 3\cdot f(u)&=& 4 \\[5pt] 27\cdot u\cdot \mathrm e^{-1,5\cdot u}&=& 4 \end{array}$

Mit dem solve-Befehl des GTR ergeben sich die Lösungen $u_1\approx 0,2$ und $u_2\approx 1,58.$

Für diese beiden Werte hat das Dreieck $OPQ_u$ einen Flächeninhalt von $4\;\text{FE}.$

(1)

(i)

Die Bedingungen $I$ und $II$ stellen sicher, dass es sich bei der Funktion $t$ um die Tangente an den Graphen der Funktion $f$ im Punkt $R$ handelt bzw. dass der Übergang „knickfrei“ erfolgt.

(ii)

Mit dem ersten Integral wird der Inhalt der Fläche zwischen dem Graphen von $f$ und der $x$ -Achse über dem Intervall $[0 ; z]$ berechnet. Mit dem zweiten Integral wird der Inhalt der Fläche zwischen dem Graphen von $t$ und der $x$ -Achse über dem Intervall $[z ;c ]$ berechnet, wobei $c$ die Nullstelle der Funktion $t$ ist. Die Addition ergibt den Flächeninhalt der in der Aufgabe beschriebenen Fläche.

(2)

$f(0,9428)\approx 2,0629$

$\(f$

Somit lautet die Gleichung der Funktion:

$\begin{array}[t]{rll} t(x)&=& -0,9063\cdot (x-0,9063)+2,0629 \\[5pt] &=& -0,9063\cdot x+2,9174 \end{array}$

(1)

(i)

Mit dem GTR folgen die Koordinaten des Hochpunktes mit $H(0,38\mid 3,83)$ und die Koordinaten des Schnittpunktes der Graphen $f$ und $g$ mit $S(1\mid 2).$

(ii)

(2)

Alle Werte im Intervall $(1,5;2,6)$ können für $k$ eingesetzt werden. $k=2$ ist beispielsweise eine Lösung.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?