Aufgabe 5
Abbildung 1 zeigt schematisch die achsensymmetrische Seitenansicht einer Hängebrücke. Die beiden vertikalen Pfeiler haben einen Abstand von 
Die Wasseroberfläche liegt 
unterhalb der Fahrbahn.
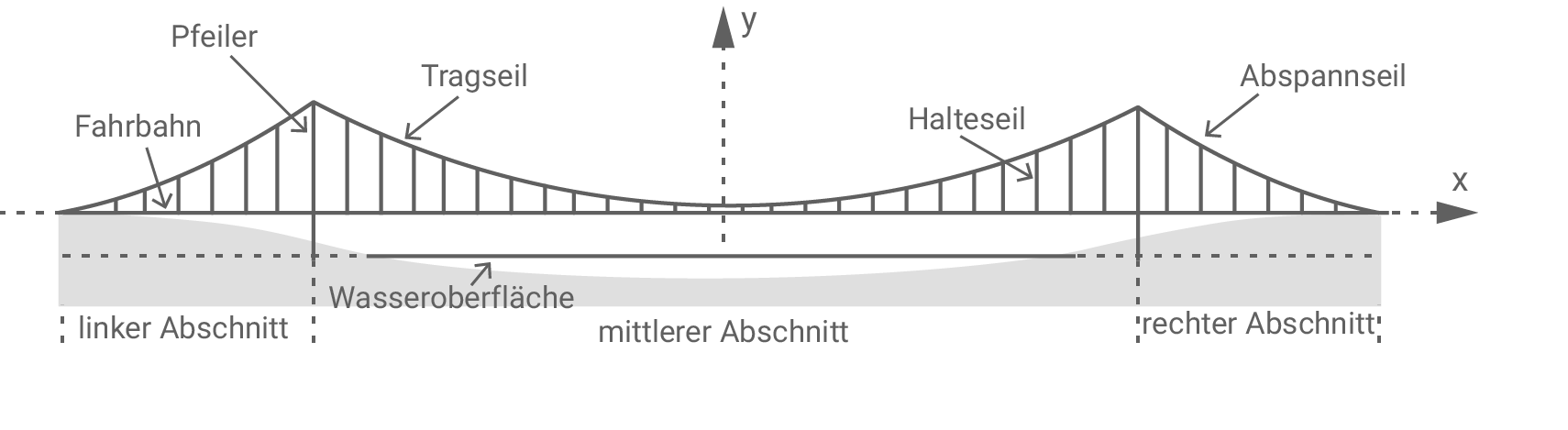
Die beiden Pfeiler gliedern die Brücke in einen linken, einen mittleren und einen rechten Abschnitt. Am oberen Ende jedes Pfeilers ist sowohl das Tragseil des mittleren Abschnitts als auch das Abspannseil des linken bzw. rechten Abschnitts befestigt. Die beiden Abspannseile sind am jeweiligen Ende der Fahrbahn verankert.
Im verwendeten Koordinatensystem entspricht eine Längeneinheit 
in der Realität. In der Seitenansicht der Brücke verläuft die 
-Achse entlang der horizontal verlaufenden Fahrbahn, die 
-Achse entlang der Symmetrieachse.
Abbildung 1
a)
Im rechten Abschnitt der Brücke wird der Verlauf des Abspannseils modellhaft durch den Funktionsterm
beschrieben.
(1)
Zeige, dass die Fahrbahn der Brücke insgesamt 
lang ist.
(2)
Auch im linken Abschnitt der Brücke kann der Verlauf des Abspannseils im Modell durch einen Funktionsterm beschrieben werden.
Gib einen passenden Term 
sowie das Intervall an, in dem dieser Term das Abspannseil darstellt.
(3)
Berechne die Höhe der Pfeiler über der Wasseroberfläche.
(4)
Weise nach: 
(5)
Untersuche rechnerisch, ob die Steigung, mit der das rechte Abspannseil auf den zugehörigen Pfeiler trifft, zwischen 
und 
liegt.
(6)
In der Seitenansicht begrenzen der rechte Pfeiler, das zugehörige Abspannseil und die Fahrbahn ein Flächenstück.
Ermittle dessen Inhalt in der Realität.
(3 + 3 + 2 + 2 + 3 + 3 Punkte)
b)
Im Folgenden wird der mittlere Abschnitt der Brücke betrachtet. Die vertikal verlaufenden Halteseile verbinden die Fahrbahn mit dem Tragseil. Sie haben sowohl von den Pfeilern als auch untereinander einen horizontalen Abstand von 
Der Verlauf des Tragseils wird modellhaft durch den Funktionsterm
beschrieben.
(1)
Begründe, dass der Term von 
damit in Einklang steht, dass die Seitenansicht der Brücke achsensymmetrisch ist.
(2)
Zwei Punkte des Tragseils in der rechten Hälfte des mittleren Abschnitts haben einen horizontalen Abstand von 
und einen Höhenunterschied von 
Gib eine Gleichung an, deren Lösung die -Koordinate des höher liegenden Punkts im Modell ist.
(2 + 2 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
Die Stelle, an der der Graph der Funktion 
die -Achse schneidet, entspricht im Modell der Stelle, an der das rechte Abspannseil endet.
![\(\begin{array}[t]{rll}
r(x)&=&0 \\[5pt]
\dfrac{253}{100} \cdot\left( \mathrm e ^{\frac{1}{11}(32-x)}-1\right)&=& 0
\end{array}\)](https://mathjax.schullv.de/46d897fcebc573f89d1b4189ca8f4f15532cc968ae6d1ede59c47737261cfb57?color=5a5a5a)
Mit dem GTR ergibt sich ![\(x=32 \;\text{[LE]}.\)](https://mathjax.schullv.de/6039f5d02e3f5300a587e896347045292db4883310aa73962aa51c4dbc143fba?color=5a5a5a)
Aufgrund der Symmetrie der Brücke, ergibt sich die Länge der Fahrbahn zu 
(2)
Aufgrund der durch die Symmetrieachse verlaufenden -Achse folgt:
![\(\begin{array}[t]{rll}
l(x)&=& r(-x) \\[5pt]
&=&\dfrac{253}{100}\cdot \mathrm e ^{\frac{1}{11} \cdot(32+x)}- \dfrac{253}{100}
\end{array}\)](https://mathjax.schullv.de/52e80e43132afa1e5d04a936a49a8371b2bd54ac16627cc6d6a44d99fdad0912?color=5a5a5a)
für 
(3)
Mit 
folgt, dass die Höhe der Pfeiler über der Wasseroberfläche ungefähr 
beträgt.
(4)
Ableitung mittels Kettenregel bestimmen:
(5)
Steigung an der Stelle 
Der Wert liegt zwischen und 
(6)
Die Fläche wird im Modell durch 
(Position des Pfeilers) und die Nullstelle bei 
(Ende des Abspannseils) begrenzt.
Daraus folgt mit dem GTR:
Der Flächeninhalt beträgt etwa 
b)
(1)
Die Funktion ist eine ganzrationale Funktion, deren Funktionsterm nur Potenzen von mit geraden Exponenten enthält.
(2)
Es gilt:
