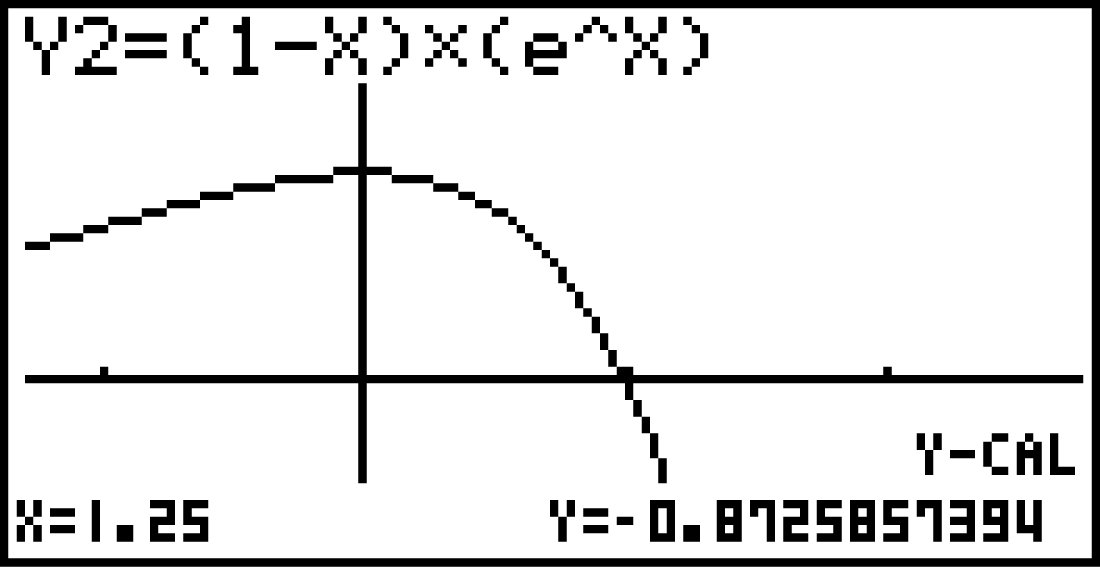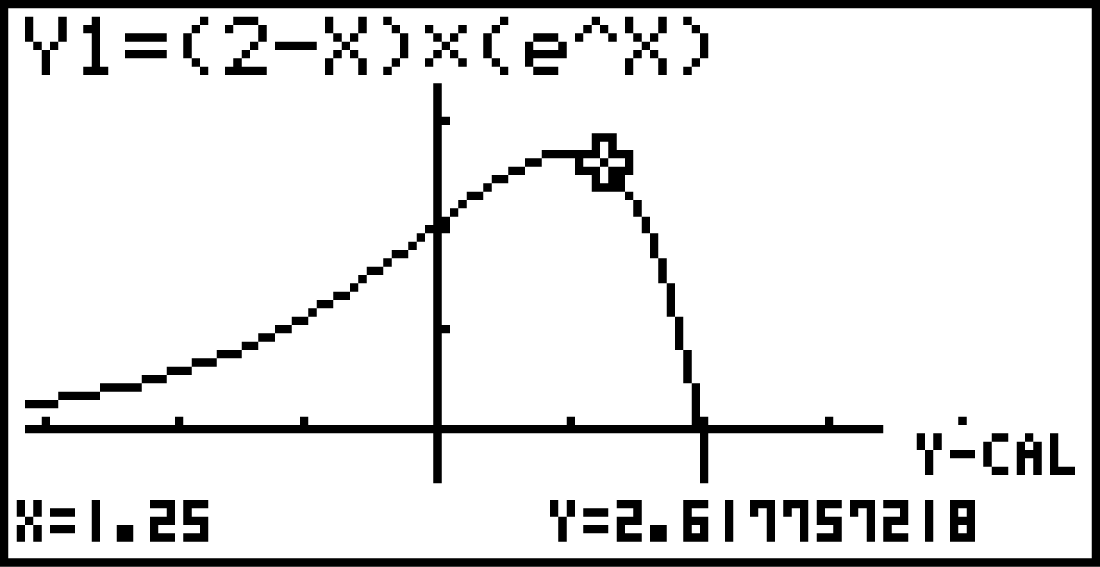Aufgabe 1
Die Funktion  ist gegeben durch
ist gegeben durch  .
.
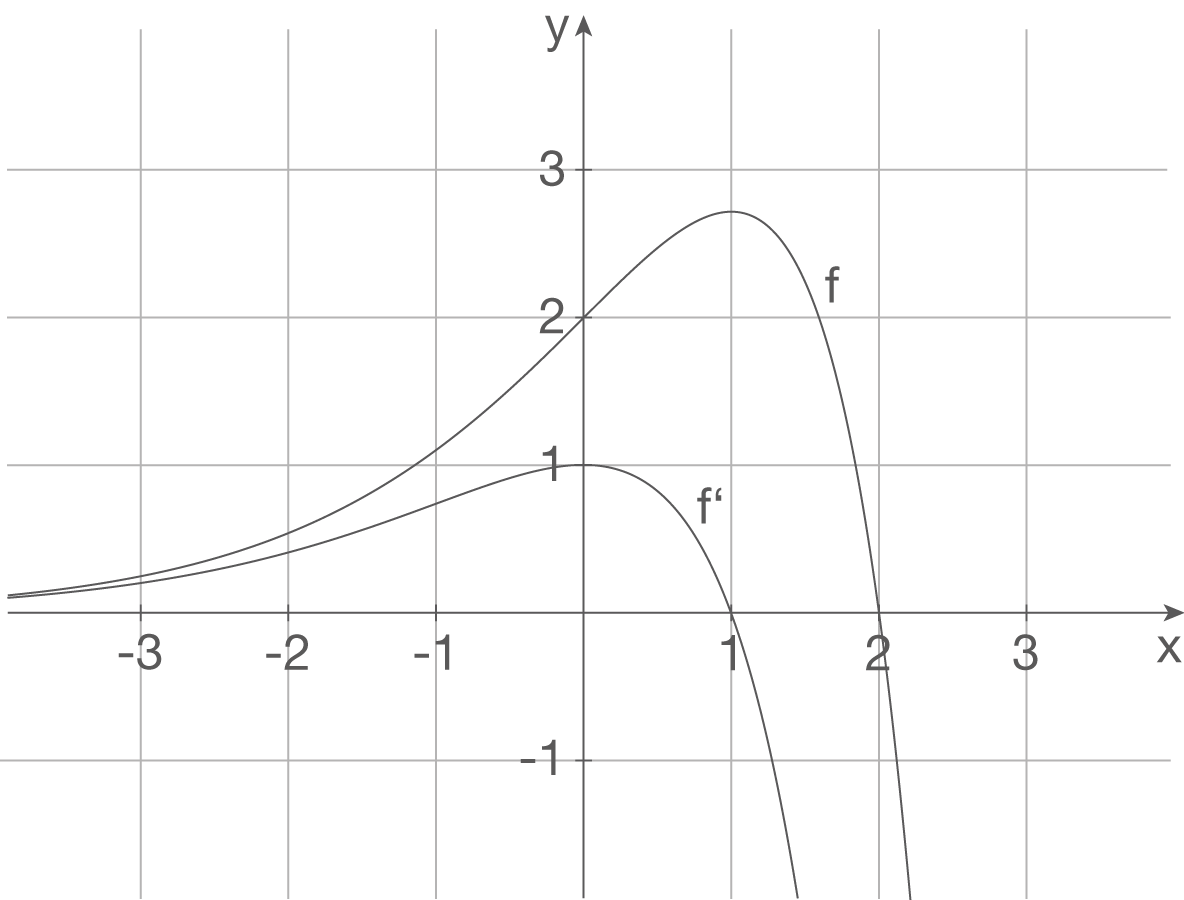
Die Graphen der Funktion und ihrer Ableitungsfunktion
und ihrer Ableitungsfunktion  sind in der Abbildung dargestellt.
sind in der Abbildung dargestellt.
Die Graphen der Funktion
a)
- Berechnen Sie die Koordinaten der Schnittpunkte des Graphen von
mit den Koordinatenachsen.
- Bestimmen Sie rechnerisch die Koordinaten der Extrem- und Wendepunkte des Graphen von
.
[Zur Kontrolle:]
- Untersuchen Sie, ob sich die Graphen der Funktionen
und
schneiden.
(5P + 16P + 4P)
b)
- Zeigen Sie, dass die Funktion
mit der Gleichung
eine Stammfunktion von
ist.
- Ermitteln Sie für
den Inhalt
der zwischen dem Graphen von
und der x-Achse im Intervall [0;z] eingeschlossenen Fläche in Abhängigkeit von z.
[Zur Kontrolle:]
(4P + 6P)
c) Auf einem Erdölfeld wird Öl gefördert. Durch die Funktion  wird nun für
wird nun für  die Förderrate1 von Beginn des Jahres 2013 bis Ende des Jahres 2014 modelliert. Dabei wird
die Förderrate1 von Beginn des Jahres 2013 bis Ende des Jahres 2014 modelliert. Dabei wird  als Maßzahl der Zeit zur Einheit 1 Jahr und
als Maßzahl der Zeit zur Einheit 1 Jahr und  als Maßzahl der Förderrate zur Einheit 1 Million Tonnen pro Jahr aufgefasst.
als Maßzahl der Förderrate zur Einheit 1 Million Tonnen pro Jahr aufgefasst.
- Beschreiben Sie den Verlauf des Graphen von
im Intervall [0;2] im Sachzusammenhang.
- Bestimmen Sie die für den gesamten Zeitraum von Beginn des Jahres 2013 bis Ende des Jahres 2014 zu erwartende Fördermenge.
- Am Endes des ersten Quartals 2014 erkennt der Betreiber, dass die Förderrate von diesem Zeitpunkt an - im Gegensatz zur Modellierung durch die Funktion
- bis zum Ende der Ölförderung linear abnehmen wird. Zur Darstellung der Förderrate für die verbleibende Dauer der Ölförderung wird daher eine lineare Funktion
gesucht, deren Graph zum Zeitpunkt
dieselbe Steigung hat wie der Graph der Funktion
.
Ermitteln Sie eine Gleichung dieser Funktion.
Berechnen Sie den Zeitpunkt, zu dem die Ölförderung enden wird.\vspace{.2cm}
[Zur Kontrolle:]
1 Unter Förderrate ist stets die momentane Förderrate zu verstehen.
(3P + 4P + 8P)
a) (1)  Schnittpunkte mit den Koordinatenachsen berechnen
Deine Aufgabe ist es hier, die Schnittpunkte des Graphen von
Schnittpunkte mit den Koordinatenachsen berechnen
Deine Aufgabe ist es hier, die Schnittpunkte des Graphen von  mit den Koordinatenachsen zu bestimmen. Dabei gilt folgendes:
mit den Koordinatenachsen zu bestimmen. Dabei gilt folgendes:
 Du suchst hier die Nullstelle der Funktion
Du suchst hier die Nullstelle der Funktion  mit
mit  .
.
 Lösungsweg A: Handschriftlich
Durch Gleichsetzen des Funktionsterms mit Null erhältst du folgende Gleichung, die du nach
Lösungsweg A: Handschriftlich
Durch Gleichsetzen des Funktionsterms mit Null erhältst du folgende Gleichung, die du nach  lösen kannst:
lösen kannst:
 Die einzige Nullstelle von
Die einzige Nullstelle von  liegt bei
liegt bei  . Damit lautet der Schnittpunkt des Graphen von
. Damit lautet der Schnittpunkt des Graphen von  mit der
mit der  -Achse
-Achse  .
.
 Lösungsweg B: GTR
Den Schnittpunkt des Graphen von
Lösungsweg B: GTR
Den Schnittpunkt des Graphen von  mit der
mit der  -Achse kannst du mit Hilfe des Graph-Menüs in deinem GTR berechnen. Gib dazu zunächst den Funktionsterm
-Achse kannst du mit Hilfe des Graph-Menüs in deinem GTR berechnen. Gib dazu zunächst den Funktionsterm  im Y=-Menü ein und lass dir den zugehörigen Graphen anzeigen.
Anschließend kannst du unter folgendem Befehl die Nullstellen bestimmen:
im Y=-Menü ein und lass dir den zugehörigen Graphen anzeigen.
Anschließend kannst du unter folgendem Befehl die Nullstellen bestimmen:
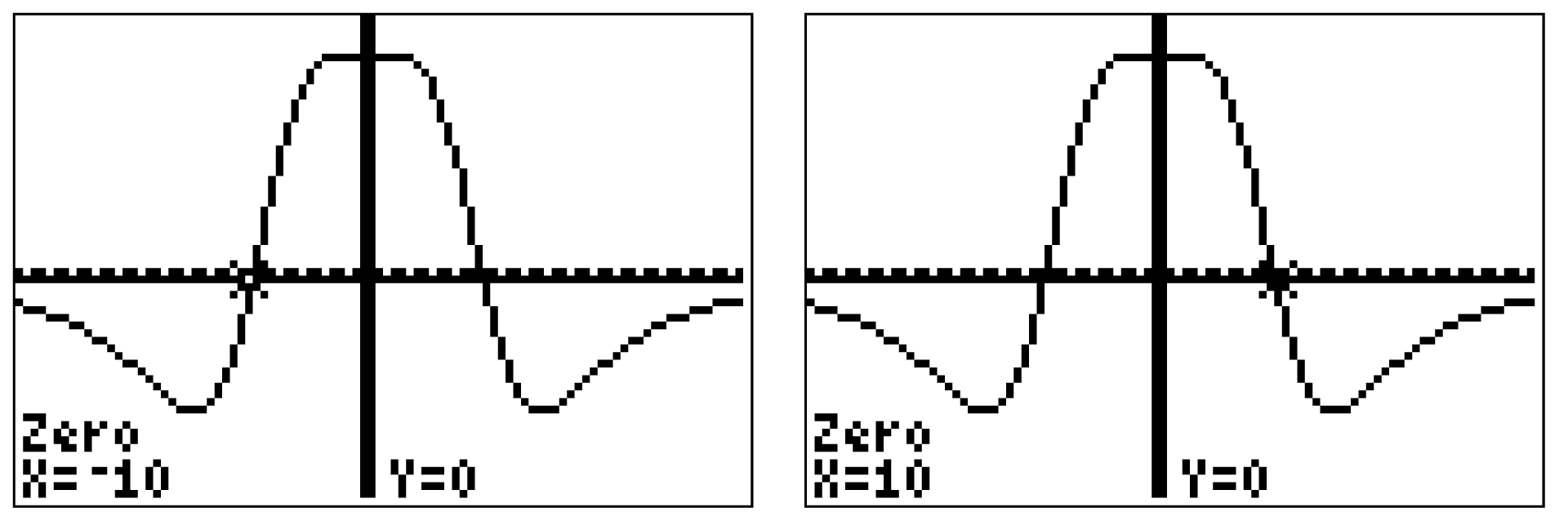
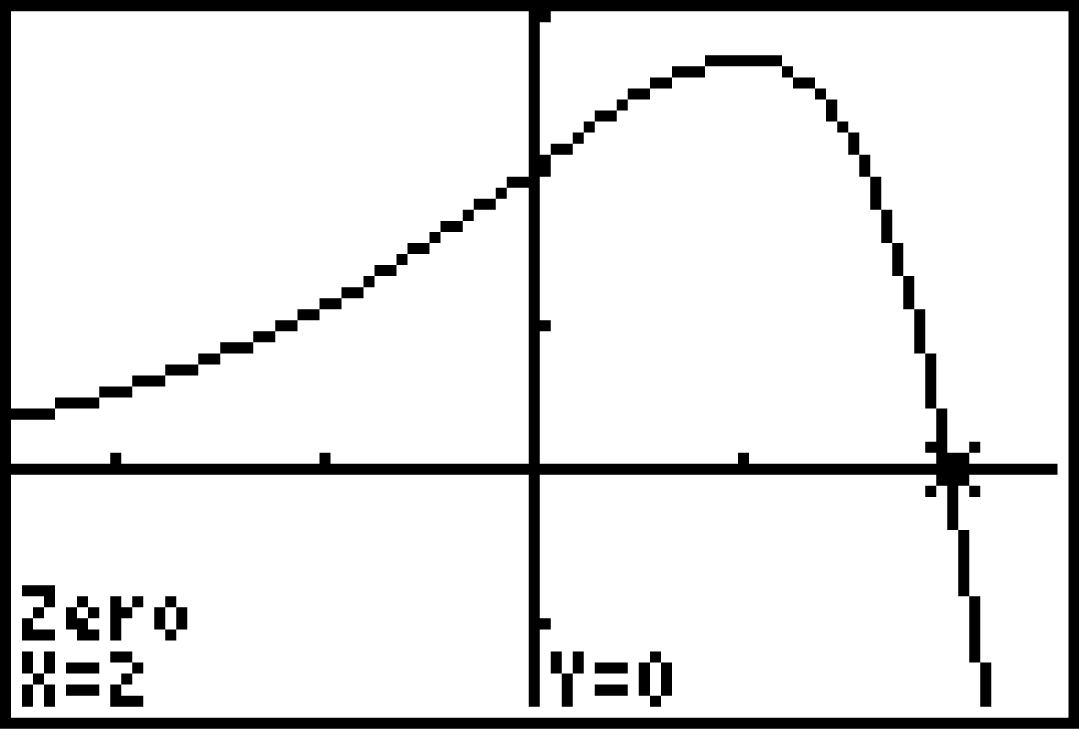 Du erhältst das Ergebnis:
Du erhältst das Ergebnis:  ,
,  Die Koordinaten des Schnittpunkts des Graphen von
Die Koordinaten des Schnittpunkts des Graphen von  mit der
mit der  -Achse lauten
-Achse lauten  .
.
 Auch hier kannst du sowohl handschriftlich, als auch mit dem GTR arbeiten um
Auch hier kannst du sowohl handschriftlich, als auch mit dem GTR arbeiten um  zu berechnen.
zu berechnen.
 Lösungsweg A: Handschriftlich
Setze nun
Lösungsweg A: Handschriftlich
Setze nun  in den Funktionsterm von
in den Funktionsterm von  ein:
ein:
 Damit lauten die Koordinaten des Schnittpunkts des Graphen von
Damit lauten die Koordinaten des Schnittpunkts des Graphen von  mit der
mit der  -Achse
-Achse  .
.
 Lösungsweg B: GTR
Lösungsweg B: GTR
 kannst du ebenfalls mit dem GTR berechnen, wenn du dir zuerst den Graphen von
kannst du ebenfalls mit dem GTR berechnen, wenn du dir zuerst den Graphen von  anzeigen lässt.
Anschließend kannst du folgendermaßen eine
anzeigen lässt.
Anschließend kannst du folgendermaßen eine  -Koordinate, in diesem Fall
-Koordinate, in diesem Fall  , eingeben:
, eingeben:
 Die Koordinaten des Schnittpunkts des Graphen von
Die Koordinaten des Schnittpunkts des Graphen von  mit der
mit der  -Achse lauten
-Achse lauten  .
(2)
.
(2)  Koordinaten der Extrempunkte bestimmen
Das Wort rechnerisch bedeutet hier, dass du die Extrempunkte nicht mit deinem GTR berechnen sollst.
Für einen Extrempunkt
Koordinaten der Extrempunkte bestimmen
Das Wort rechnerisch bedeutet hier, dass du die Extrempunkte nicht mit deinem GTR berechnen sollst.
Für einen Extrempunkt  des Graphen einer Funktion
des Graphen einer Funktion  gibt es zwei Bedingungen:
gibt es zwei Bedingungen:
 benötigst.
Gehe also wie folgt vor:
benötigst.
Gehe also wie folgt vor:
 um ein Produkt handelt. Um die erste Ableitungsfunktion zu bilden kannst du also die Produktregel verwenden. Diese lautet:
um ein Produkt handelt. Um die erste Ableitungsfunktion zu bilden kannst du also die Produktregel verwenden. Diese lautet:




 f‘(x) =
f‘(x) =


 Bildest du nun zuerst die erste Ableitung von
Bildest du nun zuerst die erste Ableitung von  , so ergeben sich
, so ergeben sich  und
und  wie folgt:
wie folgt:
 bilden:
bilden:
 Wie du sehen kannst, ist der Funktionsterm der ersten Ableitung von
Wie du sehen kannst, ist der Funktionsterm der ersten Ableitung von  immernoch ein Produkt. Verwende also zum Bilden der zweiten Ableitungsfunktion wieder die Produktregel. Hierbei ergeben sich
immernoch ein Produkt. Verwende also zum Bilden der zweiten Ableitungsfunktion wieder die Produktregel. Hierbei ergeben sich  und
und  wie folgt:
wie folgt:
 bilden:
bilden:
 2. Schritt: Notwendiges Kriterium anwenden
Wende nun das notwendige Kriterium an, indem du
2. Schritt: Notwendiges Kriterium anwenden
Wende nun das notwendige Kriterium an, indem du  setzt und die Gleichung nach
setzt und die Gleichung nach  löst:
löst:
 Der Graph von
Der Graph von  besitzt also nur eine mögliche Extremstelle bei
besitzt also nur eine mögliche Extremstelle bei  .
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun
.
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun  in
in  ein, um zu überprüfen, ob es sich bei
ein, um zu überprüfen, ob es sich bei  tatsächlich um eine Extremstelle handelt:
tatsächlich um eine Extremstelle handelt:
 An der Stelle
An der Stelle  liegt also tatsächlich ein Extrempunkt vor, und zwar ein Hochpunkt.
4. Schritt:
liegt also tatsächlich ein Extrempunkt vor, und zwar ein Hochpunkt.
4. Schritt:  -Koordinate berechnen
Du kennst nun die
-Koordinate berechnen
Du kennst nun die  -Koordinate des einzigen Extrempunkts des Graphen von
-Koordinate des einzigen Extrempunkts des Graphen von  . Setze diese nun in
. Setze diese nun in  ein, um die zugehörige
ein, um die zugehörige  -Koordinate zu berechnen:
-Koordinate zu berechnen:
 Die Koordinaten des einzigen Extrempunkts des Graphen von
Die Koordinaten des einzigen Extrempunkts des Graphen von  lauten
lauten  .
.
 Koordinaten der Wendepunkte bestimmen
Diese Aufgabe sollst du ebenfalls rechnerisch lösen. Für einen Wendepunkt
Koordinaten der Wendepunkte bestimmen
Diese Aufgabe sollst du ebenfalls rechnerisch lösen. Für einen Wendepunkt  des Graphen einer Funktion
des Graphen einer Funktion  gibt es ebenfalls zwei Kriterien, die den Kriterien für einen Extrempunkt sehr ähnlich sind:
gibt es ebenfalls zwei Kriterien, die den Kriterien für einen Extrempunkt sehr ähnlich sind:
 bereits gebildet hast, musst du nun für die Berechnung der Wendestellen nur noch die dritte Ableitung bilden. Hier kannst du ebenfalls wieder mit der Produktregel arbeiten. In diesem Fall ergeben sich
bereits gebildet hast, musst du nun für die Berechnung der Wendestellen nur noch die dritte Ableitung bilden. Hier kannst du ebenfalls wieder mit der Produktregel arbeiten. In diesem Fall ergeben sich  und
und  mit:
mit:
 bilden:
bilden:
 2. Schritt: Notwendiges Kriterium anwenden
Ermittle nun mögliche Wendestellen durch Gleichsetzen von
2. Schritt: Notwendiges Kriterium anwenden
Ermittle nun mögliche Wendestellen durch Gleichsetzen von  :
:
 Der Graph von
Der Graph von  besitzt also möglicherweise an der Stelle
besitzt also möglicherweise an der Stelle  einen Wendepunkt.
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun die mögliche Wendestelle in
einen Wendepunkt.
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun die mögliche Wendestelle in  ein um zu überprüfen, ob es sich dabei tatsächlich um eine Wendestelle handelt:
ein um zu überprüfen, ob es sich dabei tatsächlich um eine Wendestelle handelt:
 Das hinreichende Kriterium ist demnach an der Stelle
Das hinreichende Kriterium ist demnach an der Stelle  ebenfalls erfüllt und es handelt sich dabei tatsächlich um eine Wendestelle.
4. Schritt:
ebenfalls erfüllt und es handelt sich dabei tatsächlich um eine Wendestelle.
4. Schritt:  -Koordinate berechnen
Den Funktionswert von
-Koordinate berechnen
Den Funktionswert von  an der Stelle
an der Stelle  kennst du bereits aus der Berechnung der Schnittpunkte des Graphen von
kennst du bereits aus der Berechnung der Schnittpunkte des Graphen von  mit den Koordinatenachsen:
mit den Koordinatenachsen:
 Die Koordinaten des einzigen Wendepunkts des Graphen von
Die Koordinaten des einzigen Wendepunkts des Graphen von  lauten
lauten  .
(3)
.
(3)  Graphen auf Schnittpunkte untersuchen
Du sollst nun untersuchen, ob sich die Graphen von
Graphen auf Schnittpunkte untersuchen
Du sollst nun untersuchen, ob sich die Graphen von  und
und  schneiden. Die Graphen zweier Funktionen schneiden sich dann, wenn sie gemeinsame Punkte besitzen, wenn es also ein
schneiden. Die Graphen zweier Funktionen schneiden sich dann, wenn sie gemeinsame Punkte besitzen, wenn es also ein  gibt, sodass gilt:
gibt, sodass gilt:
 Dabei kannst du also so vorgehen, dass du die Funktionsterme von
Dabei kannst du also so vorgehen, dass du die Funktionsterme von  und
und  gleichsetzt und versuchst nach
gleichsetzt und versuchst nach  zu lösen. Hat diese Gleichung Lösungen, so schneiden sich die beiden Graphen, hat sie keine Lösungen, so gibt es keinen Schnittpunkt.
zu lösen. Hat diese Gleichung Lösungen, so schneiden sich die beiden Graphen, hat sie keine Lösungen, so gibt es keinen Schnittpunkt.
 Es gibt also kein
Es gibt also kein  , welches diese Gleichung erfüllt. Damit existiert kein Schnittpunkt der Graphen von
, welches diese Gleichung erfüllt. Damit existiert kein Schnittpunkt der Graphen von  und
und  .
.
- Der Schnittpunkt
mit der
-Achse ergibt sich über die Nullstelle
und hat folgende Koordinaten:
- Der Schnittpunkt
mit der
-Achse hat die Koordinaten
: Setze den Funktionsterm von
gleich Null und löse nach
auf, so erhältst du
: Berechne
um die
-Koordinate des Schnittpunkts zu bestimmen
2ND  TRACE(CALC)
TRACE(CALC)  2: zero
2: zero



2ND  TRACE(CALC)
TRACE(CALC)  1: value
1: value
Dann erhältst du das Ergebnis:
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
. Gilt
, so liegt an der Stelle
ein Hochpunkt. Gilt
, so liegt an der Stelle
ein Tiefpunkt.
- Bilde die Funktionsterme der ersten und zweiten Ableitung von
mit Hilfe der Produktregel.
- Setze
und bestimme so mögliche Extremstellen.
- Überprüfe das hinreichende Kriterium, indem du die möglichen Extremstellen in
einsetzt.
- Berechne die
-Koordinaten der Extrempunkte
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
- Bilden der dritten Ableitungsfunktion
.
- Notwendiges Kriterium anwenden durch Gleichsetzen von
und so mögliche Wendestellen ermitteln.
- Hinreichendes Kriterium überprüfen durch Einsetzen von
in
.
-Koordinaten der Wendepunkte berechnen
b) (1)  Zeigen, dass
Zeigen, dass  eine Stammfunktion von
eine Stammfunktion von  ist
Du weißt, dass die Ableitung
ist
Du weißt, dass die Ableitung  einer Stammfunktion
einer Stammfunktion  einer Funktion
einer Funktion  wieder die ursprüngliche Funktion
wieder die ursprüngliche Funktion  ist. Du kannst hier also die Funktion
ist. Du kannst hier also die Funktion  ableiten. Ist
ableiten. Ist  , so ist
, so ist  eine Stammfunktion von
eine Stammfunktion von  . Dazu kannst du wieder die Produktregel verwenden.
Dabei ergeben sich
. Dazu kannst du wieder die Produktregel verwenden.
Dabei ergeben sich  und
und  hier wie folgt:
hier wie folgt:
 ergibt sich dann durch:
ergibt sich dann durch:
 Durch Ableiten von
Durch Ableiten von  ergibt sich
ergibt sich  . Demnach ist
. Demnach ist  eine Stammfunktion von
eine Stammfunktion von  .
(2)
.
(2)  Flächeninhalt berechnen
In diesem Aufgabenteil sollst du den Inhalt
Flächeninhalt berechnen
In diesem Aufgabenteil sollst du den Inhalt  der Fläche berechnen, die von dem Graphen von
der Fläche berechnen, die von dem Graphen von  und der
und der  -Achse im Intervall
-Achse im Intervall ![\( \left[0;z\right]\)](https://mathjax.schullv.de/6572543b73594f39eb5a744308107f3983a66ab48190456bf2355f5180f74446?color=5a5a5a) eingeschlossen wird.
Solch einen Flächeninhalt kannst du mit einem Integral berechnen. Dabei musst du von Nullstelle zu Nullstelle integrieren, damit sich nicht Flächenstücke unterhalb und oberhalb der
eingeschlossen wird.
Solch einen Flächeninhalt kannst du mit einem Integral berechnen. Dabei musst du von Nullstelle zu Nullstelle integrieren, damit sich nicht Flächenstücke unterhalb und oberhalb der  -Achse gegenseitig beim Integrieren aufheben können. In diesem Fall, liegt aber keine Nullstelle innerhalb des Intervalls, da du weißt, dass die Nullstelle von
-Achse gegenseitig beim Integrieren aufheben können. In diesem Fall, liegt aber keine Nullstelle innerhalb des Intervalls, da du weißt, dass die Nullstelle von  bei
bei  liegt. Das Intervall über welches du integrieren sollst, reicht maximal bis zur Nullstelle hin.
Deine Integrationsgrenzen sind demnach gegeben durch
liegt. Das Intervall über welches du integrieren sollst, reicht maximal bis zur Nullstelle hin.
Deine Integrationsgrenzen sind demnach gegeben durch  und
und  .
Demnach ist hier der Wert des folgenden Integrals gesucht:
.
Demnach ist hier der Wert des folgenden Integrals gesucht:
 Um dies zu berechnen, benötigst du eine Stammfunktion von
Um dies zu berechnen, benötigst du eine Stammfunktion von  . Eine solche kennst du aus dem vorigen Aufgabenteil bereits. Dann ergibt sich:
. Eine solche kennst du aus dem vorigen Aufgabenteil bereits. Dann ergibt sich:
![\( \begin{array}{rll}
A(z)&=&\displaystyle\int_{0}^{z}f(x)\mathrm dx \\
&=&\left[F(x)\right]_0^z\\
&=&F(z)- F(0) \\
&=&(3-z)\cdot\mathrm e^z- (3-0)\cdot\mathrm e^0 \\
&=&(3-z)\cdot\mathrm e^z-3\cdot1 \\
&=&(3-z) \cdot \mathrm e^z-3 \\
\end{array}\)](https://mathjax.schullv.de/6d2fbaca9216b3f74382b26d275b865e2d3ddcfcac64bea363bd50606a468c9b?color=5a5a5a) Der Inhalt der Fläche zwischen dem Graphen von
Der Inhalt der Fläche zwischen dem Graphen von  und der
und der  -Achse im Intervall
-Achse im Intervall ![\( \left[0;z\right]\)](https://mathjax.schullv.de/6572543b73594f39eb5a744308107f3983a66ab48190456bf2355f5180f74446?color=5a5a5a) ist gegeben durch
ist gegeben durch  .
.
c) (1)  Verlauf des Graphen im Sachzusammenhang beschreiben
Hier ist es deine Aufgabe, den Verlauf des Graphen von
Verlauf des Graphen im Sachzusammenhang beschreiben
Hier ist es deine Aufgabe, den Verlauf des Graphen von  im Intervall
im Intervall ![\( \left[0;2\right]\)](https://mathjax.schullv.de/2457cbbc4d324c1dd92f8987b0cc07b7ceeb9b4def8ca113f5f42e0d9ace1944?color=5a5a5a) im Sachzusammenhang zu beschreiben. Dabei kannst du wie folgt vorgehen:
im Sachzusammenhang zu beschreiben. Dabei kannst du wie folgt vorgehen:
 zuerst stark ansteigt und dann im Punkt
zuerst stark ansteigt und dann im Punkt  das Maximum erreicht. Anschließend fällt der Graph steil ab bis er an der Stelle
das Maximum erreicht. Anschließend fällt der Graph steil ab bis er an der Stelle  den Wert Null erreicht.
2. Schritt: Übertragung auf den Sachzusammenhang
Da
den Wert Null erreicht.
2. Schritt: Übertragung auf den Sachzusammenhang
Da  die momentane Förderungsrate beschreibt, also sozusagen die Geschwindigkeit der Förderung angibt, kannst du den Verlauf des Graphen wie folgt auf den Sachzusammenhang übertragen:
die momentane Förderungsrate beschreibt, also sozusagen die Geschwindigkeit der Förderung angibt, kannst du den Verlauf des Graphen wie folgt auf den Sachzusammenhang übertragen:
 Zu erwartende Fördermenge berechnen
Deine Aufgabe ist es nun, die zu erwartende Fördermenge in den beiden Jahren 2013 und 2014 zu berechnen. Da
Zu erwartende Fördermenge berechnen
Deine Aufgabe ist es nun, die zu erwartende Fördermenge in den beiden Jahren 2013 und 2014 zu berechnen. Da  die Förderungsrate beschreibt, wird die Menge des geförderten Öls vom Zeitpunkt
die Förderungsrate beschreibt, wird die Menge des geförderten Öls vom Zeitpunkt  bis zum Zeitpunkt
bis zum Zeitpunkt  durch folgendes Integral beschrieben, welches du bereits aus dem vorigen Aufgabenteil kennst:
durch folgendes Integral beschrieben, welches du bereits aus dem vorigen Aufgabenteil kennst:
 Deine Integrationsgrenzen sind in diesem Fall nun
Deine Integrationsgrenzen sind in diesem Fall nun  und
und  . Setzt du diese Grenzen ein, so sollte dir eine gewisse Ähnlichkeit zum Aufgabenteil b) (2) auffallen:
. Setzt du diese Grenzen ein, so sollte dir eine gewisse Ähnlichkeit zum Aufgabenteil b) (2) auffallen:
 Dies entspricht nämlich genau
Dies entspricht nämlich genau  mit
mit  .
Gesucht ist hier also
.
Gesucht ist hier also  . Dies kannst du durch einsetzen berechnen:
. Dies kannst du durch einsetzen berechnen:
 Die zu erwartende Fördermenge von Beginn des Jahres 2013 bis zum Ende des Jahres 2014 beträgt
Die zu erwartende Fördermenge von Beginn des Jahres 2013 bis zum Ende des Jahres 2014 beträgt  Tonnen.
(3)
Tonnen.
(3)  Lineare Funktion bestimmen
Nun sollst du eine lineare Funktion
Lineare Funktion bestimmen
Nun sollst du eine lineare Funktion  bestimmen, die die Förderungsrate vom Zeitpunkt
bestimmen, die die Förderungsrate vom Zeitpunkt  bis zum Ende der Ölförderung beschreibt. Das Ende der Ölförderung ist durch die neue Darstellung durch die Funktion
bis zum Ende der Ölförderung beschreibt. Das Ende der Ölförderung ist durch die neue Darstellung durch die Funktion  nun nicht mehr
nun nicht mehr  sondern eine Nullstelle von
sondern eine Nullstelle von  .
Du hast dabei folgende Informationen über
.
Du hast dabei folgende Informationen über  gegeben:
gegeben:
 wird immer durch deren erste Ableitung
wird immer durch deren erste Ableitung  beschrieben. Bei einer linearen Funktion ist die Steigung konstant, also an jeder Stelle gleich, und wird genau durch den Wert
beschrieben. Bei einer linearen Funktion ist die Steigung konstant, also an jeder Stelle gleich, und wird genau durch den Wert  beschrieben. Du kannst die Informationen wie folgt formulieren:
beschrieben. Du kannst die Informationen wie folgt formulieren:
 und
und  . Diese kannst du wie folgt berechnen:
. Diese kannst du wie folgt berechnen:
 bereits kennst, kannst du nun
bereits kennst, kannst du nun  dort einsetzen und so
dort einsetzen und so  berechnen. Dies kannst du sowohl mit deinem GTR, als auch handschriftlich tun.
berechnen. Dies kannst du sowohl mit deinem GTR, als auch handschriftlich tun.
 Lösungsweg A: Handschriftlich
Lösungsweg A: Handschriftlich
 Damit kennst du nun die Steigung von
Damit kennst du nun die Steigung von  mit
mit  . Setzt du dies in
. Setzt du dies in  ein, so erhältst du:
ein, so erhältst du:

 Lösungsweg B: GTR
Wie schon im ersten Aufgabenteil, kannst du nun
Lösungsweg B: GTR
Wie schon im ersten Aufgabenteil, kannst du nun  im Graph-Modus deines GTR berechnen, indem du dir den Graphen von
im Graph-Modus deines GTR berechnen, indem du dir den Graphen von  anzeigen lässt und anschließend
anzeigen lässt und anschließend
 eingibst.
eingibst.
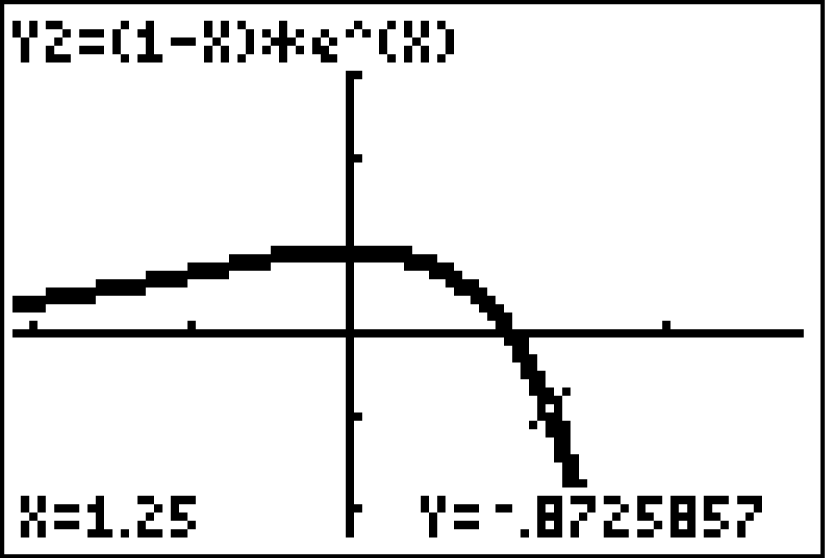 Dann erhältst du das Ergebnis:
Dann erhältst du das Ergebnis:
 Setzt du dies schon einmal in die Funktionsgleichung von
Setzt du dies schon einmal in die Funktionsgleichung von  ein, so erhältst du:
ein, so erhältst du:
 .
2. Schritt: Punktprobe
Berechne nun die Koordinaten des Punkts
.
2. Schritt: Punktprobe
Berechne nun die Koordinaten des Punkts  , indem du
, indem du  in
in  einsetzt und führe anschließend eine Punktprobe mit der Funktion
einsetzt und führe anschließend eine Punktprobe mit der Funktion  durch. Dabei kannst du ebenfalls wieder mit dem GTR oder handschriftlich arbeiten.
durch. Dabei kannst du ebenfalls wieder mit dem GTR oder handschriftlich arbeiten.
 Lösungsweg A: Handschriftlich
Lösungsweg A: Handschriftlich
 Damit weißt du nun, dass der Punkt des Graphen von
Damit weißt du nun, dass der Punkt des Graphen von  mit den Koordinaten
mit den Koordinaten  auf dem Graphen von
auf dem Graphen von  liegen soll und kannst somit eine Punktprobe durchführen und nach
liegen soll und kannst somit eine Punktprobe durchführen und nach  lösen:
lösen:
 Setzt du diesen Wert nun in die Funktionsgleichung ein, so erhältst du:
Setzt du diesen Wert nun in die Funktionsgleichung ein, so erhältst du:
 Eine Funktionsgleichung der Funktion
Eine Funktionsgleichung der Funktion  lautet
lautet  .
.
 Lösungsweg B: GTR
Lösungsweg B: GTR
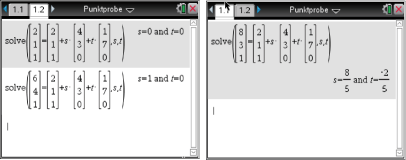 Berechnest du
Berechnest du  wie zuvor mit dem GTR, so erhältst du das Ergebnis:
wie zuvor mit dem GTR, so erhältst du das Ergebnis:
 Der Punkt
Der Punkt  des Graphen von
des Graphen von  soll ebenfalls auf dem Graphen von
soll ebenfalls auf dem Graphen von  liegen. Daher kannst du nun eine Punktprobe durchführen und so
liegen. Daher kannst du nun eine Punktprobe durchführen und so  berechnen:
berechnen:
 Setzt du dies nun in
Setzt du dies nun in  ein, so erhältst du die folgende Funktionsgleichung:
ein, so erhältst du die folgende Funktionsgleichung:
 Eine Funktionsgleichung von
Eine Funktionsgleichung von  lautet
lautet  .
.
 Ende der Ölförderung berechnen
Deine Aufgabe ist es, den Zeitpunkt zu bestimmen, zu dem die Ölförderung enden wird. Die Ölförderung endet genau dann, wenn die Förderungsrate den Wert Null erreicht, denn dann werden Null Tonnen pro Jahr gefördert. Du suchst hier also die Nullstelle der Funktion
Ende der Ölförderung berechnen
Deine Aufgabe ist es, den Zeitpunkt zu bestimmen, zu dem die Ölförderung enden wird. Die Ölförderung endet genau dann, wenn die Förderungsrate den Wert Null erreicht, denn dann werden Null Tonnen pro Jahr gefördert. Du suchst hier also die Nullstelle der Funktion  . Diese kannst du wieder handschriftlich oder aber mit dem GTR durch Gleichsetzen des Funktiosterms von
. Diese kannst du wieder handschriftlich oder aber mit dem GTR durch Gleichsetzen des Funktiosterms von  mit Null bestimmen. Nutze hier in jedem Fall das Kontrollergebnis für die Funktionsgleichung von
mit Null bestimmen. Nutze hier in jedem Fall das Kontrollergebnis für die Funktionsgleichung von  , damit dein Wert so genau wie möglich ausfällt.
, damit dein Wert so genau wie möglich ausfällt.
 Lösungsweg A: Handschriftlich
Lösungsweg A: Handschriftlich
 Die Ölförderung endet nach
Die Ölförderung endet nach  Jahren, also am 31. März 2017.
Jahren, also am 31. März 2017.
 Lösungsweg B: GTR
Lösungsweg B: GTR
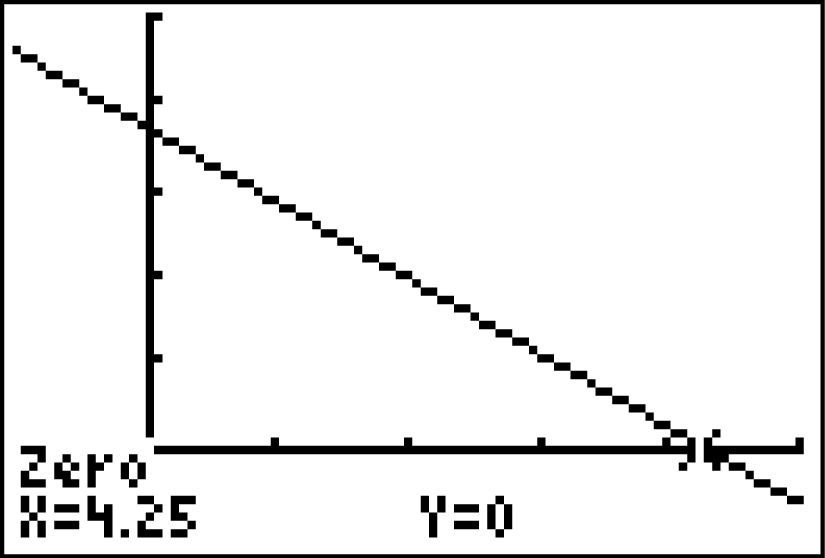 Du kannst die Nullstelle von
Du kannst die Nullstelle von  wieder mit Hilfe des Graph-Menüs deines GTR berechnen. Du erhältst dann das Ergebnis:
wieder mit Hilfe des Graph-Menüs deines GTR berechnen. Du erhältst dann das Ergebnis:
 Die Ölförderung endet nach
Die Ölförderung endet nach  Jahren, also am 31. März 2017.
Jahren, also am 31. März 2017.
- Beschreibe den Verlauf des Graphen von
allgemein
- Übertrage die Informationen aus dem 1. Schritt auf den Sachzusammenhang mit Hilfe der Information, dass
die momentane Förderrate beschreibt.
- Im ersten Jahr nimmt die Förderungsrate des Öls stark zu, das heißt es wird immer schneller Öl gefördert.
- Am schnellsten verläuft die Förderung nach genau einem Jahr, dort hat der Graph von
sein Maximum erreicht.
- Anschließend nimmt die Förderungsrate ab. Das bedeutet, die Förderung verläuft immer langsamer bis sie nach genau zwei Jahren still liegt, also kein Öl mehr gefördert wird.
ist linear.
soll an der Stelle
den gleichen Funktionswert wie
besitzen.
soll an der Stelle
die gleiche Steigung wie
besitzen.
hat die Form
- Berechne
und setze dies bereits in die Funktionsgleichung von
ein.
- Berechne
und führe eine Punktprobe mit dem Punkt
durch, um
zu berechnen.
2ND  TRACE(CALC)
TRACE(CALC)  1: value
1: value
wählst und 


a) (1)  Schnittpunkte mit den Koordinatenachsen berechnen
Deine Aufgabe ist es hier, die Schnittpunkte des Graphen von
Schnittpunkte mit den Koordinatenachsen berechnen
Deine Aufgabe ist es hier, die Schnittpunkte des Graphen von  mit den Koordinatenachsen zu bestimmen. Dabei gilt folgendes:
mit den Koordinatenachsen zu bestimmen. Dabei gilt folgendes:
 Du suchst hier die Nullstelle der Funktion
Du suchst hier die Nullstelle der Funktion  mit
mit  .
.
 Lösungsweg A: Handschriftlich
Durch Gleichsetzen des Funktionsterms mit Null erhältst du folgende Gleichung, die du nach
Lösungsweg A: Handschriftlich
Durch Gleichsetzen des Funktionsterms mit Null erhältst du folgende Gleichung, die du nach  lösen kannst:
lösen kannst:
 Die einzige Nullstelle von
Die einzige Nullstelle von  liegt bei
liegt bei  . Damit lautet der Schnittpunkt des Graphen von
. Damit lautet der Schnittpunkt des Graphen von  mit der
mit der  -Achse
-Achse  .
.
 Lösungsweg B: GTR
Den Schnittpunkt des Graphen von
Lösungsweg B: GTR
Den Schnittpunkt des Graphen von  mit der
mit der  -Achse kannst du mit Hilfe des Graph-Menüs in deinem GTR berechnen. Gib dazu zunächst den Funktionsterm
-Achse kannst du mit Hilfe des Graph-Menüs in deinem GTR berechnen. Gib dazu zunächst den Funktionsterm  dort ein und lass dir den zugehörigen Graphen anzeigen.
Anschließend kannst du unter folgendem Befehl die Nullstellen bestimmen:
dort ein und lass dir den zugehörigen Graphen anzeigen.
Anschließend kannst du unter folgendem Befehl die Nullstellen bestimmen:
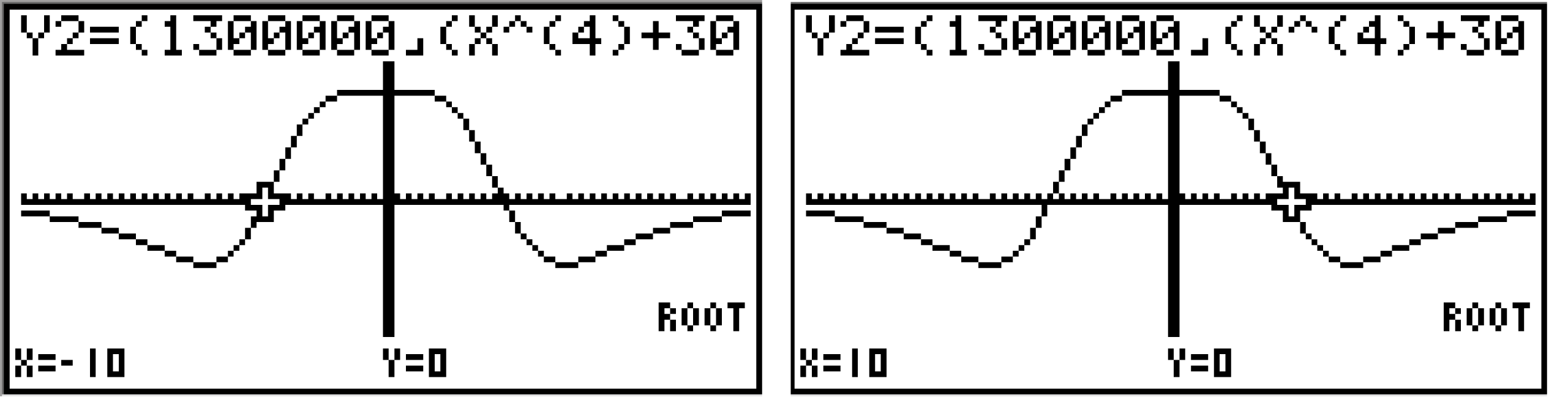
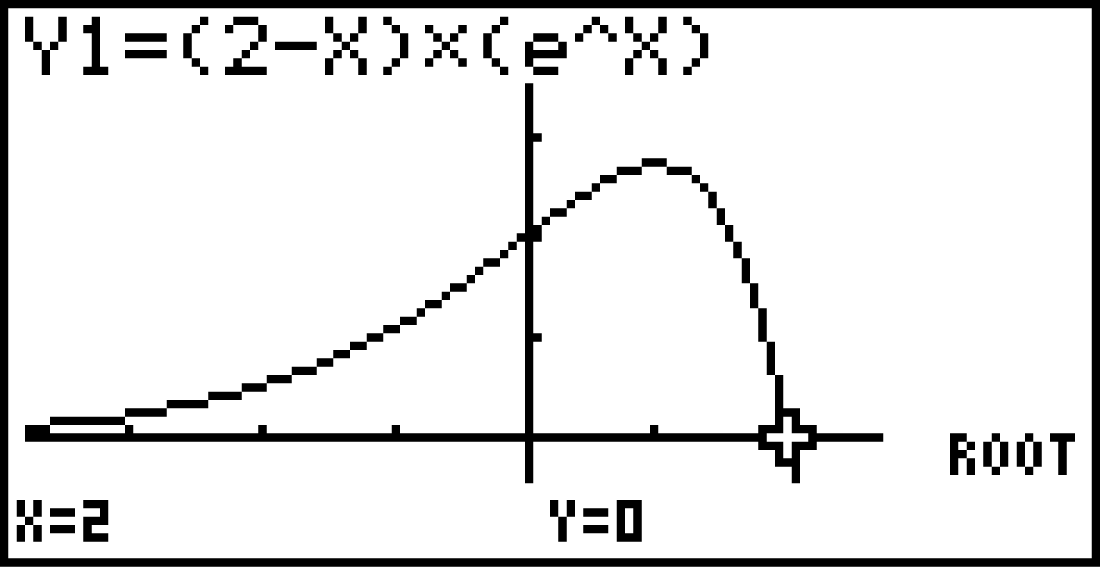 Du erhältst das Ergebnis:
Du erhältst das Ergebnis:  ,
,  Die Koordinaten des Schnittpunkts des Graphen von
Die Koordinaten des Schnittpunkts des Graphen von  mit der
mit der  -Achse lauten
-Achse lauten  .
.
 Auch hier kannst du sowohl handschriftlich, als auch mit dem GTR arbeiten um
Auch hier kannst du sowohl handschriftlich, als auch mit dem GTR arbeiten um  zu berechnen.
zu berechnen.
 Lösungsweg A: Handschriftlich
Setze nun
Lösungsweg A: Handschriftlich
Setze nun  in den Funktionsterm von
in den Funktionsterm von  ein:
ein:
 Damit lauten die Koordinaten des Schnittpunkts des Graphen von
Damit lauten die Koordinaten des Schnittpunkts des Graphen von  mit der
mit der  -Achse
-Achse  .
.
 Lösungsweg B: GTR
Lösungsweg B: GTR
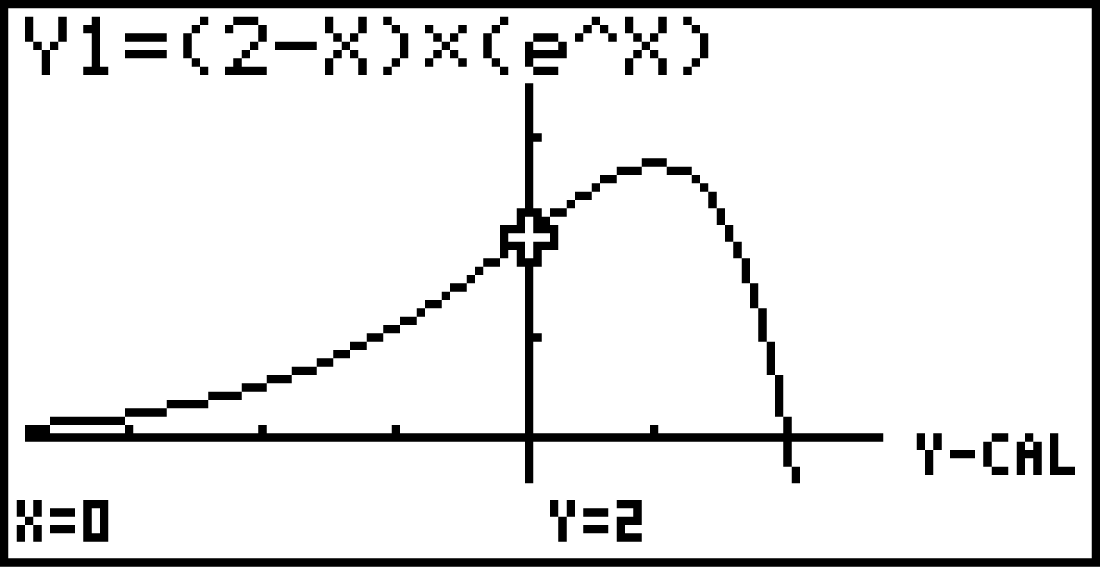
 kannst du ebenfalls mit dem GTR berechnen, wenn du dir zuerst den Graphen von
kannst du ebenfalls mit dem GTR berechnen, wenn du dir zuerst den Graphen von  anzeigen lässt.
Anschließend kannst du folgendermaßen eine
anzeigen lässt.
Anschließend kannst du folgendermaßen eine  -Koordinate, in diesem Fall
-Koordinate, in diesem Fall  , eingeben:
, eingeben:
 Die Koordinaten des Schnittpunkts des Graphen von
Die Koordinaten des Schnittpunkts des Graphen von  mit der
mit der  -Achse lauten
-Achse lauten  .
(2)
.
(2)  Koordinaten der Extrempunkte bestimmen
Das Wort rechnerisch bedeutet hier, dass du die Extrempunkte nicht mit deinem GTR berechnen sollst.
Für einen Extrempunkt
Koordinaten der Extrempunkte bestimmen
Das Wort rechnerisch bedeutet hier, dass du die Extrempunkte nicht mit deinem GTR berechnen sollst.
Für einen Extrempunkt  des Graphen einer Funktion
des Graphen einer Funktion  gibt es zwei Bedingungen:
gibt es zwei Bedingungen:
 benötigst.
Gehe also wie folgt vor:
benötigst.
Gehe also wie folgt vor:
 um ein Produkt handelt. Um die erste Ableitungsfunktion zu bilden kannst du also die Produktregel verwenden. Diese lautet:
um ein Produkt handelt. Um die erste Ableitungsfunktion zu bilden kannst du also die Produktregel verwenden. Diese lautet:




 f‘(x) =
f‘(x) =


 Bildest du nun zuerst die erste Ableitung von
Bildest du nun zuerst die erste Ableitung von  , so ergeben sich
, so ergeben sich  und
und  wie folgt:
wie folgt:
 bilden:
bilden:
 Wie du sehen kannst, ist der Funktionsterm der ersten Ableitung von
Wie du sehen kannst, ist der Funktionsterm der ersten Ableitung von  immernoch ein Produkt. Verwende also zum Bilden der zweiten Ableitungsfunktion wieder die Produktregel. Hierbei ergeben sich
immernoch ein Produkt. Verwende also zum Bilden der zweiten Ableitungsfunktion wieder die Produktregel. Hierbei ergeben sich  und
und  wie folgt:
wie folgt:
 bilden:
bilden:
 2. Schritt: Notwendiges Kriterium anwenden
Wende nun das notwendige Kriterium an, indem du
2. Schritt: Notwendiges Kriterium anwenden
Wende nun das notwendige Kriterium an, indem du  setzt und die Gleichung nach
setzt und die Gleichung nach  löst:
löst:
 Der Graph von
Der Graph von  besitzt also nur eine mögliche Extremstelle bei
besitzt also nur eine mögliche Extremstelle bei  .
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun
.
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun  in
in  ein, um zu überprüfen, ob es sich bei
ein, um zu überprüfen, ob es sich bei  tatsächlich um eine Extremstelle handelt:
tatsächlich um eine Extremstelle handelt:
 An der Stelle
An der Stelle  liegt also tatsächlich ein Extrempunkt vor, und zwar ein Hochpunkt.
4. Schritt:
liegt also tatsächlich ein Extrempunkt vor, und zwar ein Hochpunkt.
4. Schritt:  -Koordinate berechnen
Du kennst nun die
-Koordinate berechnen
Du kennst nun die  -Koordinate des einzigen Extrempunkts des Graphen von
-Koordinate des einzigen Extrempunkts des Graphen von  . Setze diese nun in
. Setze diese nun in  ein, um die zugehörige
ein, um die zugehörige  -Koordinate zu berechnen:
-Koordinate zu berechnen:
 Die Koordinaten des einzigen Extrempunkts des Graphen von
Die Koordinaten des einzigen Extrempunkts des Graphen von  lauten
lauten  .
.
 Koordinaten der Wendepunkte bestimmen
Diese Aufgabe sollst du ebenfalls rechnerisch lösen. Für einen Wendepunkt
Koordinaten der Wendepunkte bestimmen
Diese Aufgabe sollst du ebenfalls rechnerisch lösen. Für einen Wendepunkt  des Graphen einer Funktion
des Graphen einer Funktion  gibt es ebenfalls zwei Kriterien, die den Kriterien für einen Extrempunkt sehr ähnlich sind:
gibt es ebenfalls zwei Kriterien, die den Kriterien für einen Extrempunkt sehr ähnlich sind:
 bereits gebildet hast, musst du nun für die Berechnung der Wendestellen nur noch die dritte Ableitung bilden. Hier kannst du ebenfalls wieder mit der Produktregel arbeiten. In diesem Fall ergeben sich
bereits gebildet hast, musst du nun für die Berechnung der Wendestellen nur noch die dritte Ableitung bilden. Hier kannst du ebenfalls wieder mit der Produktregel arbeiten. In diesem Fall ergeben sich  und
und  mit:
mit:
 bilden:
bilden:
 2. Schritt: Notwendiges Kriterium anwenden
Ermittle nun mögliche Wendestellen durch Gleichsetzen von
2. Schritt: Notwendiges Kriterium anwenden
Ermittle nun mögliche Wendestellen durch Gleichsetzen von  :
:
 Der Graph von
Der Graph von  besitzt also möglicherweise an der Stelle
besitzt also möglicherweise an der Stelle  einen Wendepunkt.
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun die mögliche Wendestelle in
einen Wendepunkt.
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun die mögliche Wendestelle in  ein um zu überprüfen, ob es sich dabei tatsächlich um eine Wendestelle handelt:
ein um zu überprüfen, ob es sich dabei tatsächlich um eine Wendestelle handelt:
 Das hinreichende Kriterium ist demnach an der Stelle
Das hinreichende Kriterium ist demnach an der Stelle  ebenfalls erfüllt und es handelt sich dabei tatsächlich um eine Wendestelle.
4. Schritt:
ebenfalls erfüllt und es handelt sich dabei tatsächlich um eine Wendestelle.
4. Schritt:  -Koordinate berechnen
Den Funktionswert von
-Koordinate berechnen
Den Funktionswert von  an der Stelle
an der Stelle  kennst du bereits aus der Berechnung der Schnittpunkte des Graphen von
kennst du bereits aus der Berechnung der Schnittpunkte des Graphen von  mit den Koordinatenachsen:
mit den Koordinatenachsen:
 Die Koordinaten des einzigen Wendepunkts des Graphen von
Die Koordinaten des einzigen Wendepunkts des Graphen von  lauten
lauten  .
(3)
.
(3)  Graphen auf Schnittpunkte untersuchen
Du sollst nun untersuchen, ob sich die Graphen von
Graphen auf Schnittpunkte untersuchen
Du sollst nun untersuchen, ob sich die Graphen von  und
und  schneiden. Die Graphen zweier Funktionen schneiden sich dann, wenn sie gemeinsame Punkte besitzen, wenn es also ein
schneiden. Die Graphen zweier Funktionen schneiden sich dann, wenn sie gemeinsame Punkte besitzen, wenn es also ein  gibt, sodass gilt:
gibt, sodass gilt:
 Dabei kannst du also so vorgehen, dass du die Funktionsterme von
Dabei kannst du also so vorgehen, dass du die Funktionsterme von  und
und  gleichsetzt und versuchst nach
gleichsetzt und versuchst nach  zu lösen. Hat diese Gleichung Lösungen, so schneiden sich die beiden Graphen, hat sie keine Lösungen, so gibt es keinen Schnittpunkt.
zu lösen. Hat diese Gleichung Lösungen, so schneiden sich die beiden Graphen, hat sie keine Lösungen, so gibt es keinen Schnittpunkt.
 Es gibt also kein
Es gibt also kein  , welches diese Gleichung erfüllt. Damit existiert kein Schnittpunkt der Graphen von
, welches diese Gleichung erfüllt. Damit existiert kein Schnittpunkt der Graphen von  und
und  .
.
- Der Schnittpunkt
mit der
-Achse ergibt sich über die Nullstelle
und hat folgende Koordinaten:
- Der Schnittpunkt
mit der
-Achse hat die Koordinaten
: Setze den Funktionsterm von
gleich Null und löse nach
auf, so erhältst du
: Berechne
um die
-Koordinate des Schnittpunkts zu bestimmen
F5(G-Solv)  F1: ROOT
F1: ROOT

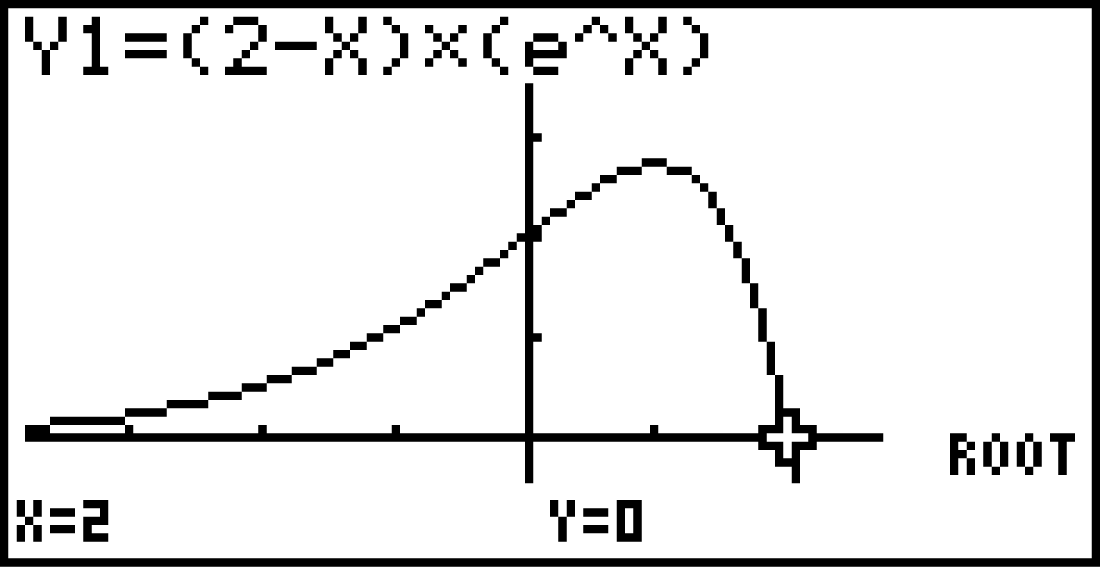

F5(G-Solv)  F6
F6  F1: Y-CAL
F1: Y-CAL
Dann erhältst du das Ergebnis:
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
. Gilt
, so liegt an der Stelle
ein Hochpunkt. Gilt
, so liegt an der Stelle
ein Tiefpunkt.
- Bilde die Funktionsterme der ersten und zweiten Ableitung von
mit Hilfe der Produktregel.
- Setze
und bestimme so mögliche Extremstellen.
- Überprüfe das hinreichende Kriterium, indem du die möglichen Extremstellen in
einsetzt.
- Berechne die
-Koordinaten der Extrempunkte
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
- Bilden der dritten Ableitungsfunktion
.
- Notwendiges Kriterium anwenden durch Gleichsetzen von
und so mögliche Wendestellen ermitteln.
- Hinreichendes Kriterium überprüfen durch Einsetzen von
in
.
-Koordinaten der Wendepunkte berechnen
b) (1)  Zeigen, dass
Zeigen, dass  eine Stammfunktion von
eine Stammfunktion von  ist
Du weißt, dass die Ableitung
ist
Du weißt, dass die Ableitung  einer Stammfunktion
einer Stammfunktion  einer Funktion
einer Funktion  wieder die ursprüngliche Funktion
wieder die ursprüngliche Funktion  ist. Du kannst hier also die Funktion
ist. Du kannst hier also die Funktion  ableiten. Ist
ableiten. Ist  , so ist
, so ist  eine Stammfunktion von
eine Stammfunktion von  . Dazu kannst du wieder die Produktregel verwenden.
Dabei ergeben sich
. Dazu kannst du wieder die Produktregel verwenden.
Dabei ergeben sich  und
und  hier wie folgt:
hier wie folgt:
 ergibt sich dann durch:
ergibt sich dann durch:
 Durch Ableiten von
Durch Ableiten von  ergibt sich
ergibt sich  . Demnach ist
. Demnach ist  eine Stammfunktion von
eine Stammfunktion von  .
(2)
.
(2)  Flächeninhalt berechnen
In diesem Aufgabenteil sollst du den Inhalt
Flächeninhalt berechnen
In diesem Aufgabenteil sollst du den Inhalt  der Fläche berechnen, die von dem Graphen von
der Fläche berechnen, die von dem Graphen von  und der
und der  -Achse im Intervall
-Achse im Intervall ![\(\left[0;z\right]\)](https://mathjax.schullv.de/a00c510e61e0f479a4db70b3b2c6ef5250afe8a3d824347fe87fd02fb0cf372c?color=5a5a5a) eingeschlossen wird.
Solch einen Flächeninhalt kannst du mit einem Integral berechnen. Dabei musst du von Nullstelle zu Nullstelle integrieren, damit sich nicht Flächenstücke unterhalb und oberhalb der
eingeschlossen wird.
Solch einen Flächeninhalt kannst du mit einem Integral berechnen. Dabei musst du von Nullstelle zu Nullstelle integrieren, damit sich nicht Flächenstücke unterhalb und oberhalb der  -Achse gegenseitig beim Integrieren aufheben können. In diesem Fall, liegt aber keine Nullstelle innerhalb des Intervalls, da du weißt, dass die Nullstelle von
-Achse gegenseitig beim Integrieren aufheben können. In diesem Fall, liegt aber keine Nullstelle innerhalb des Intervalls, da du weißt, dass die Nullstelle von  bei
bei  liegt. Das Intervall über welches du integrieren sollst, reicht maximal bis zur Nullstelle hin.
Deine Integrationsgrenzen sind demnach gegeben durch
liegt. Das Intervall über welches du integrieren sollst, reicht maximal bis zur Nullstelle hin.
Deine Integrationsgrenzen sind demnach gegeben durch  und
und  .
Demnach ist hier der Wert des folgenden Integrals gesucht:
.
Demnach ist hier der Wert des folgenden Integrals gesucht:
 Um dies zu berechnen, benötigst du eine Stammfunktion von
Um dies zu berechnen, benötigst du eine Stammfunktion von  . Eine solche kennst du aus dem vorigen Aufgabenteil bereits. Dann ergibt sich:
. Eine solche kennst du aus dem vorigen Aufgabenteil bereits. Dann ergibt sich:
![\(\begin{array}{rll}
A(z)&=&\displaystyle\int_{0}^{z}f(x)\mathrm dx \\
&=&\left[F(x)\right]_0^z\\
&=&F(z)- F(0) \\
&=&(3-z)\cdot\mathrm e^z- (3-0)\cdot\mathrm e^0 \\
&=&(3-z)\cdot\mathrm e^z-3\cdot1 \\
&=&(3-z) \cdot \mathrm e^z-3 \\
\end{array}\)](https://mathjax.schullv.de/5415b34f872c3a49f16ed543020814d6c464ace4defe098f301ac28262c1d979?color=5a5a5a) Der Inhalt der Fläche zwischen dem Graphen von
Der Inhalt der Fläche zwischen dem Graphen von  und der
und der  -Achse im Intervall
-Achse im Intervall ![\(\left[0;z\right]\)](https://mathjax.schullv.de/a00c510e61e0f479a4db70b3b2c6ef5250afe8a3d824347fe87fd02fb0cf372c?color=5a5a5a) ist gegeben durch
ist gegeben durch  .
.
c) (1)  Verlauf des Graphen im Sachzusammenhang beschreiben
Hier ist es deine Aufgabe, den Verlauf des Graphen von
Verlauf des Graphen im Sachzusammenhang beschreiben
Hier ist es deine Aufgabe, den Verlauf des Graphen von  im Intervall
im Intervall ![\(\left[0;2\right]\)](https://mathjax.schullv.de/b9a09a41b5c5ec1c4251ed3da41004d122c02d75d95d2ab5b8a3080687ede910?color=5a5a5a) im Sachzusammenhang zu beschreiben. Dabei kannst du wie folgt vorgehen:
im Sachzusammenhang zu beschreiben. Dabei kannst du wie folgt vorgehen:
 zuerst stark ansteigt und dann im Punkt
zuerst stark ansteigt und dann im Punkt  das Maximum erreicht. Anschließend fällt der Graph steil ab bis er an der Stelle
das Maximum erreicht. Anschließend fällt der Graph steil ab bis er an der Stelle  den Wert Null erreicht.
2. Schritt: Übertragung auf den Sachzusammenhang
Da
den Wert Null erreicht.
2. Schritt: Übertragung auf den Sachzusammenhang
Da  die momentane Förderungsrate beschreibt, also sozusagen die Geschwindigkeit der Förderung angibt, kannst du den Verlauf des Graphen wie folgt auf den Sachzusammenhang übertragen:
die momentane Förderungsrate beschreibt, also sozusagen die Geschwindigkeit der Förderung angibt, kannst du den Verlauf des Graphen wie folgt auf den Sachzusammenhang übertragen:
 Zu erwartende Fördermenge berechnen
Deine Aufgabe ist es nun, die zu erwartende Fördermenge in den beiden Jahren 2013 und 2014 zu berechnen. Da
Zu erwartende Fördermenge berechnen
Deine Aufgabe ist es nun, die zu erwartende Fördermenge in den beiden Jahren 2013 und 2014 zu berechnen. Da  die Förderungsrate beschreibt, wird die Menge des geförderten Öls vom Zeitpunkt
die Förderungsrate beschreibt, wird die Menge des geförderten Öls vom Zeitpunkt  bis zum Zeitpunkt
bis zum Zeitpunkt  durch folgendes Integral beschrieben, welches du bereits aus dem vorigen Aufgabenteil kennst:
durch folgendes Integral beschrieben, welches du bereits aus dem vorigen Aufgabenteil kennst:
 Deine Integrationsgrenzen sind in diesem Fall nun
Deine Integrationsgrenzen sind in diesem Fall nun  und
und  . Setzt du diese Grenzen ein, so sollte dir eine gewisse Ähnlichkeit zum Aufgabenteil b) (2) auffallen:
. Setzt du diese Grenzen ein, so sollte dir eine gewisse Ähnlichkeit zum Aufgabenteil b) (2) auffallen:
 Dies entspricht nämlich genau
Dies entspricht nämlich genau  mit
mit  .
Gesucht ist hier also
.
Gesucht ist hier also  . Dies kannst du durch einsetzen berechnen:
. Dies kannst du durch einsetzen berechnen:
 Die zu erwartende Fördermenge von Beginn des Jahres 2013 bis zum Ende des Jahres 2014 beträgt
Die zu erwartende Fördermenge von Beginn des Jahres 2013 bis zum Ende des Jahres 2014 beträgt  Tonnen.
(3)
Tonnen.
(3)  Lineare Funktion bestimmen
Nun sollst du eine lineare Funktion
Lineare Funktion bestimmen
Nun sollst du eine lineare Funktion  bestimmen, die die Förderungsrate vom Zeitpunkt
bestimmen, die die Förderungsrate vom Zeitpunkt  bis zum Ende der Ölförderung beschreibt. Das Ende der Ölförderung ist durch die neue Darstellung durch die Funktion
bis zum Ende der Ölförderung beschreibt. Das Ende der Ölförderung ist durch die neue Darstellung durch die Funktion  nun nicht mehr
nun nicht mehr  sondern eine Nullstelle von
sondern eine Nullstelle von  .
Du hast dabei folgende Informationen über
.
Du hast dabei folgende Informationen über  gegeben:
gegeben:
 wird immer durch deren erste Ableitung
wird immer durch deren erste Ableitung  beschrieben. Bei einer linearen Funktion ist die Steigung konstant, also an jeder Stelle gleich, und wird genau durch den Wert
beschrieben. Bei einer linearen Funktion ist die Steigung konstant, also an jeder Stelle gleich, und wird genau durch den Wert  beschrieben. Du kannst die Informationen wie folgt formulieren:
beschrieben. Du kannst die Informationen wie folgt formulieren:
 und
und  . Diese kannst du wie folgt berechnen:
. Diese kannst du wie folgt berechnen:
 bereits kennst, kannst du nun
bereits kennst, kannst du nun  dort einsetzen und so
dort einsetzen und so  berechnen. Dies kannst du sowohl mit deinem GTR, als auch handschriftlich tun.
berechnen. Dies kannst du sowohl mit deinem GTR, als auch handschriftlich tun.
 Lösungsweg A: Handschriftlich
Lösungsweg A: Handschriftlich
 Damit kennst du nun die Steigung von
Damit kennst du nun die Steigung von  mit
mit  . Setzt du dies in
. Setzt du dies in  ein, so erhältst du:
ein, so erhältst du:

 Lösungsweg B: GTR
Wie schon im ersten Aufgabenteil, kannst du nun
Lösungsweg B: GTR
Wie schon im ersten Aufgabenteil, kannst du nun  im Graph-Modus deines GTR berechnen, indem du dir den Graphen von
im Graph-Modus deines GTR berechnen, indem du dir den Graphen von  anzeigen lässt und anschließend
anzeigen lässt und anschließend
 eingibst.
eingibst.
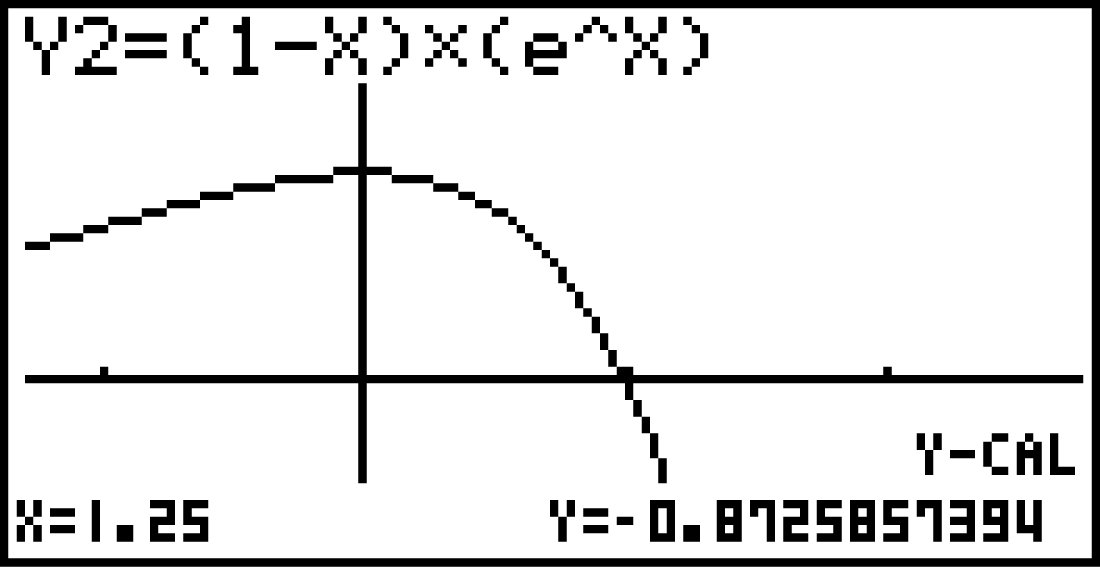 Dann erhältst du das Ergebnis:
Dann erhältst du das Ergebnis:
 Setzt du dies schon einmal in die Funktionsgleichung von
Setzt du dies schon einmal in die Funktionsgleichung von  ein, so erhältst du:
ein, so erhältst du:
 .
2. Schritt: Punktprobe
Berechne nun die Koordinaten des Punkts
.
2. Schritt: Punktprobe
Berechne nun die Koordinaten des Punkts  , indem du
, indem du  in
in  einsetzt und führe anschließend eine Punktprobe mit der Funktion
einsetzt und führe anschließend eine Punktprobe mit der Funktion  durch. Dabei kannst du ebenfalls wieder mit dem GTR oder handschriftlich arbeiten.
durch. Dabei kannst du ebenfalls wieder mit dem GTR oder handschriftlich arbeiten.
 Lösungsweg A: Handschriftlich
Lösungsweg A: Handschriftlich
 Damit weißt du nun, dass der Punkt des Graphen von
Damit weißt du nun, dass der Punkt des Graphen von  mit den Koordinaten
mit den Koordinaten  auf dem Graphen von
auf dem Graphen von  liegen soll und kannst somit eine Punktprobe durchführen und nach
liegen soll und kannst somit eine Punktprobe durchführen und nach  lösen:
lösen:
 Setzt du diesen Wert nun in die Funktionsgleichung ein, so erhältst du:
Setzt du diesen Wert nun in die Funktionsgleichung ein, so erhältst du:
 Eine Funktionsgleichung der Funktion
Eine Funktionsgleichung der Funktion  lautet
lautet  .
.
 Lösungsweg B: GTR
Lösungsweg B: GTR
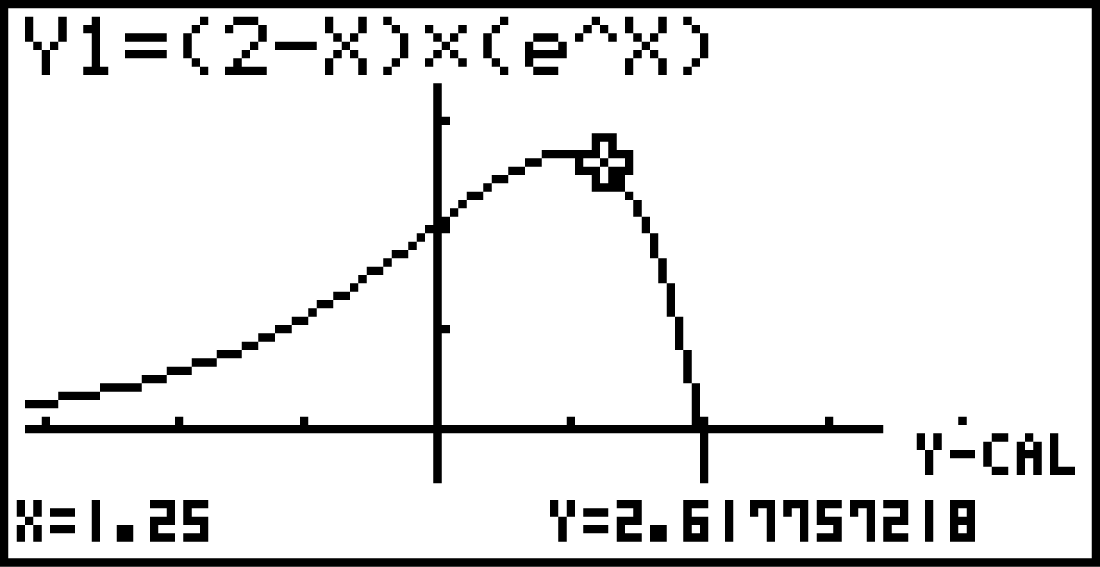 Berechnest du
Berechnest du  wie zuvor mit dem GTR, so erhältst du das Ergebnis:
wie zuvor mit dem GTR, so erhältst du das Ergebnis:
 Der Punkt
Der Punkt  des Graphen von
des Graphen von  soll ebenfalls auf dem Graphen von
soll ebenfalls auf dem Graphen von  liegen. Daher kannst du nun eine Punktprobe durchführen und so
liegen. Daher kannst du nun eine Punktprobe durchführen und so  berechnen:
berechnen:
 Setzt du dies nun in
Setzt du dies nun in  ein, so erhältst du die folgende Funktionsgleichung:
ein, so erhältst du die folgende Funktionsgleichung:
 Eine Funktionsgleichung von
Eine Funktionsgleichung von  lautet
lautet  .
.
 Ende der Ölförderung berechnen
Deine Aufgabe ist es, den Zeitpunkt zu bestimmen, zu dem die Ölförderung enden wird. Die Ölförderung endet genau dann, wenn die Förderungsrate den Wert Null erreicht, denn dann werden Null Tonnen pro Jahr gefördert. Du suchst hier also die Nullstelle der Funktion
Ende der Ölförderung berechnen
Deine Aufgabe ist es, den Zeitpunkt zu bestimmen, zu dem die Ölförderung enden wird. Die Ölförderung endet genau dann, wenn die Förderungsrate den Wert Null erreicht, denn dann werden Null Tonnen pro Jahr gefördert. Du suchst hier also die Nullstelle der Funktion  . Diese kannst du wieder handschriftlich oder aber mit dem GTR durch Gleichsetzen des Funktiosterms von
. Diese kannst du wieder handschriftlich oder aber mit dem GTR durch Gleichsetzen des Funktiosterms von  mit Null bestimmen. Nutze hier in jedem Fall das Kontrollergebnis für die Funktionsgleichung von
mit Null bestimmen. Nutze hier in jedem Fall das Kontrollergebnis für die Funktionsgleichung von  , damit dein Wert so genau wie möglich ausfällt.
, damit dein Wert so genau wie möglich ausfällt.
 Lösungsweg A: Handschriftlich
Lösungsweg A: Handschriftlich
 Die Ölförderung endet nach
Die Ölförderung endet nach  Jahren, also am 31. März 2017.
Jahren, also am 31. März 2017.
 Lösungsweg B: GTR
Lösungsweg B: GTR
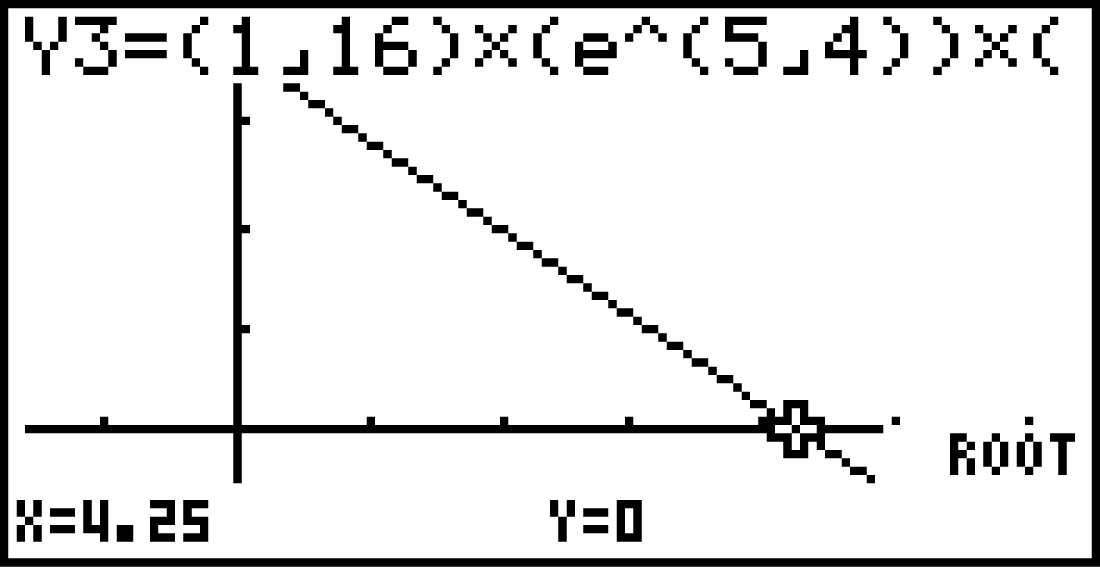 Du kannst die Nullstelle von
Du kannst die Nullstelle von  wieder mit Hilfe des Graph-Menüs deines GTR berechnen. Du erhältst dann das Ergebnis:
wieder mit Hilfe des Graph-Menüs deines GTR berechnen. Du erhältst dann das Ergebnis:
 Die Ölförderung endet nach
Die Ölförderung endet nach  Jahren, also am 31. März 2017.
Jahren, also am 31. März 2017.
- Beschreibe den Verlauf des Graphen von
allgemein
- Übertrage die Informationen aus dem 1. Schritt auf den Sachzusammenhang mit Hilfe der Information, dass
die momentane Förderrate beschreibt.
- Im ersten Jahr nimmt die Förderungsrate des Öls stark zu, das heißt es wird immer schneller Öl gefördert.
- Am schnellsten verläuft die Förderung nach genau einem Jahr, dort hat der Graph von
sein Maximum erreicht.
- Anschließend nimmt die Förderungsrate ab. Das bedeutet, die Förderung verläuft immer langsamer bis sie nach genau zwei Jahren still liegt, also kein Öl mehr gefördert wird.
ist linear.
soll an der Stelle
den gleichen Funktionswert wie
besitzen.
soll an der Stelle
die gleiche Steigung wie
besitzen.
hat die Form
- Berechne
und setze dies bereits in die Funktionsgleichung von
ein.
- Berechne
und führe eine Punktprobe mit dem Punkt
durch, um
zu berechnen.
F5(G-Solv)  F6
F6  F1: Y-CAL
F1: Y-CAL
wählst und