Aufgabe 1
Flüsse treten manchmal über ihre Ufer. Zur Vermeidung solcher Überschwemmungen werden große Wasserbecken eingesetzt, sogenannte Rückhaltebecken. Droht eine Überschwemmung, so wird ein Teil des Flusswassers in das Rückhaltebecken geleitet. Dort wird das Wasser zunächst zurückgehalten und später kontrolliert in den Fluss geleitet.
Im Folgenden soll zunächst der Zufluss in und anschließend der Abfluss des Wassers aus einem Rückhaltebecken betrachtet werden.
Zur Modellierung der momentanen Zuflussrate, mit der das Wasser des Flusses während eines Beobachtungszeitraumes von  Stunden in das Rückhaltebecken fließt, wird für
Stunden in das Rückhaltebecken fließt, wird für  die Funktion
die Funktion  mit der Gleichung
mit der Gleichung
 , mit
, mit 
verwendet. Dabei ist die Zeit seit Beobachtungsbeginn in Stunden und
die Zeit seit Beobachtungsbeginn in Stunden und  die momentane Zuflussrate in
die momentane Zuflussrate in  Wasser pro Stunde.
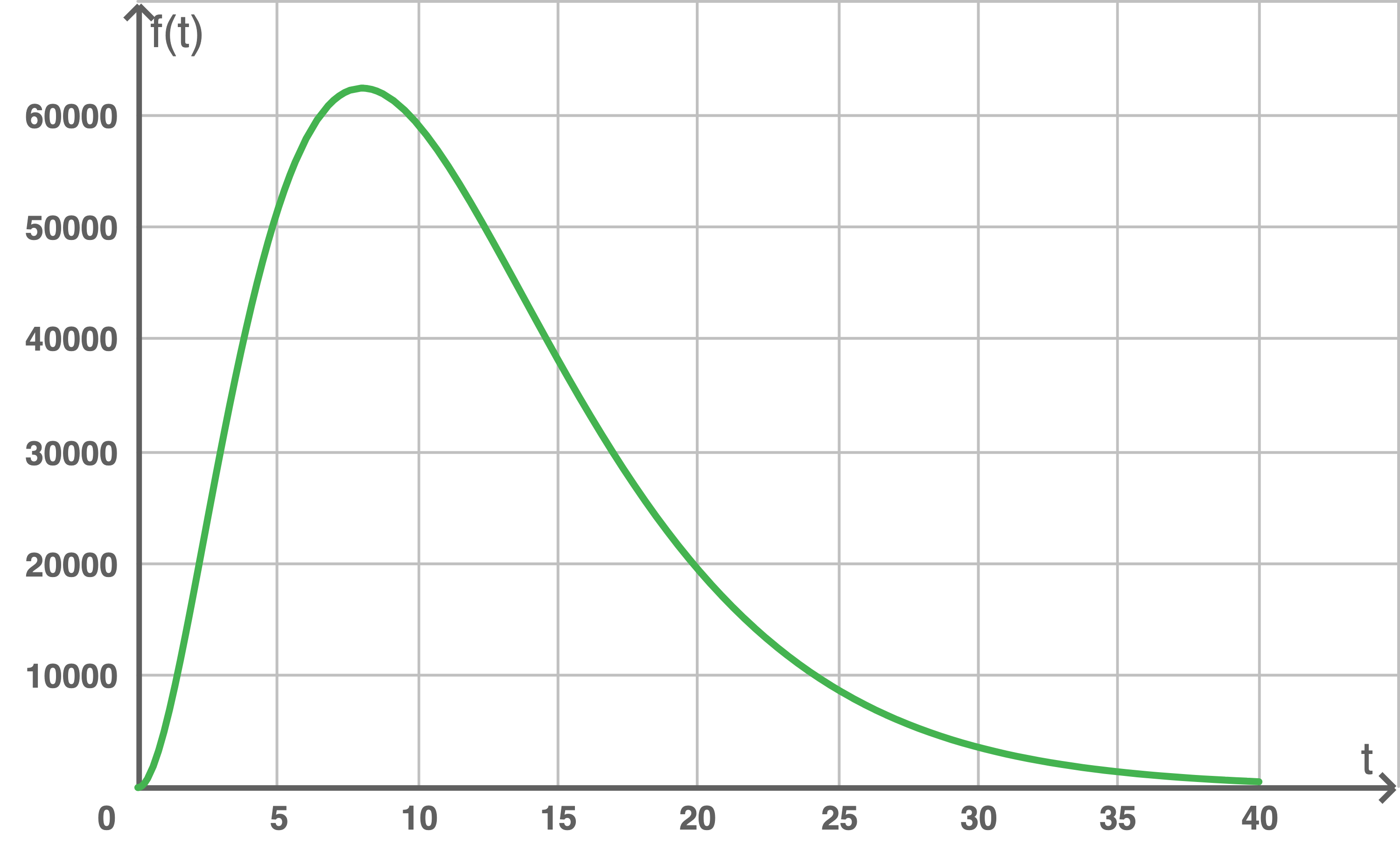
In der folgenden Abbildung 1 ist der Graph von
Wasser pro Stunde.
In der folgenden Abbildung 1 ist der Graph von  im Intervall
im Intervall ![\([0;40]\)](https://mathjax.schullv.de/92024017c23b22a74de1b9e273c916a9b37db62564aea3cef60aa5075052123a?color=5a5a5a) dargestellt.
dargestellt.
verwendet. Dabei ist

Abbildung 1
a)
(1)
Gib den Funktionswert von  an der Stelle
an der Stelle  an und interpretiere diesen Wert im Sachzusammenhang.
an und interpretiere diesen Wert im Sachzusammenhang.
(2)
Weise rechnerisch nach, dass die momentane Zuflussrate im Modell  Stunden nach Beobachtungsbeginn maximal ist, und gib die maximale momentane Zuflussrate an.
Stunden nach Beobachtungsbeginn maximal ist, und gib die maximale momentane Zuflussrate an.
(3+7 Punkte)
b)
Ermittle, wie viel Wasser im Beobachtungszeitraum von  Stunden in das Rückhaltebecken fließt.
Stunden in das Rückhaltebecken fließt.
(4 Punkte)
c)
Die momentane Abflussrate vom Rückhaltebecken in den Fluss im Beobachtungszeitraum wird für  durch die Funktion
durch die Funktion  mit der Gleichung
mit der Gleichung
 , mit
, mit  modelliert. Dabei ist
modelliert. Dabei ist  die momentane Abflussrate in
die momentane Abflussrate in  Wasser pro Stunde.
Wasser pro Stunde.
(1)
Ermittle das Zeitintervall im Beobachtungszeitraum, in dem die momentane Abflussrate größer als  Wasser pro Stunde ist.
Wasser pro Stunde ist.
(2)
Bestimme den Zeitpunkt im Beobachtungszeitraum, zu dem die momentane Abflussrate am stärksten zunimmt.
(3)
Bestimme den Zeitpunkt, bis zu dem seit Beobachtungsbeginn  Wasser aus dem Becken fließen.
Wasser aus dem Becken fließen.
(4 + 5 + 4 Punkte)
d)
Der Graph von  und der Graph von
und der Graph von  sind in der Abbildung 2 dargestellt.
sind in der Abbildung 2 dargestellt.
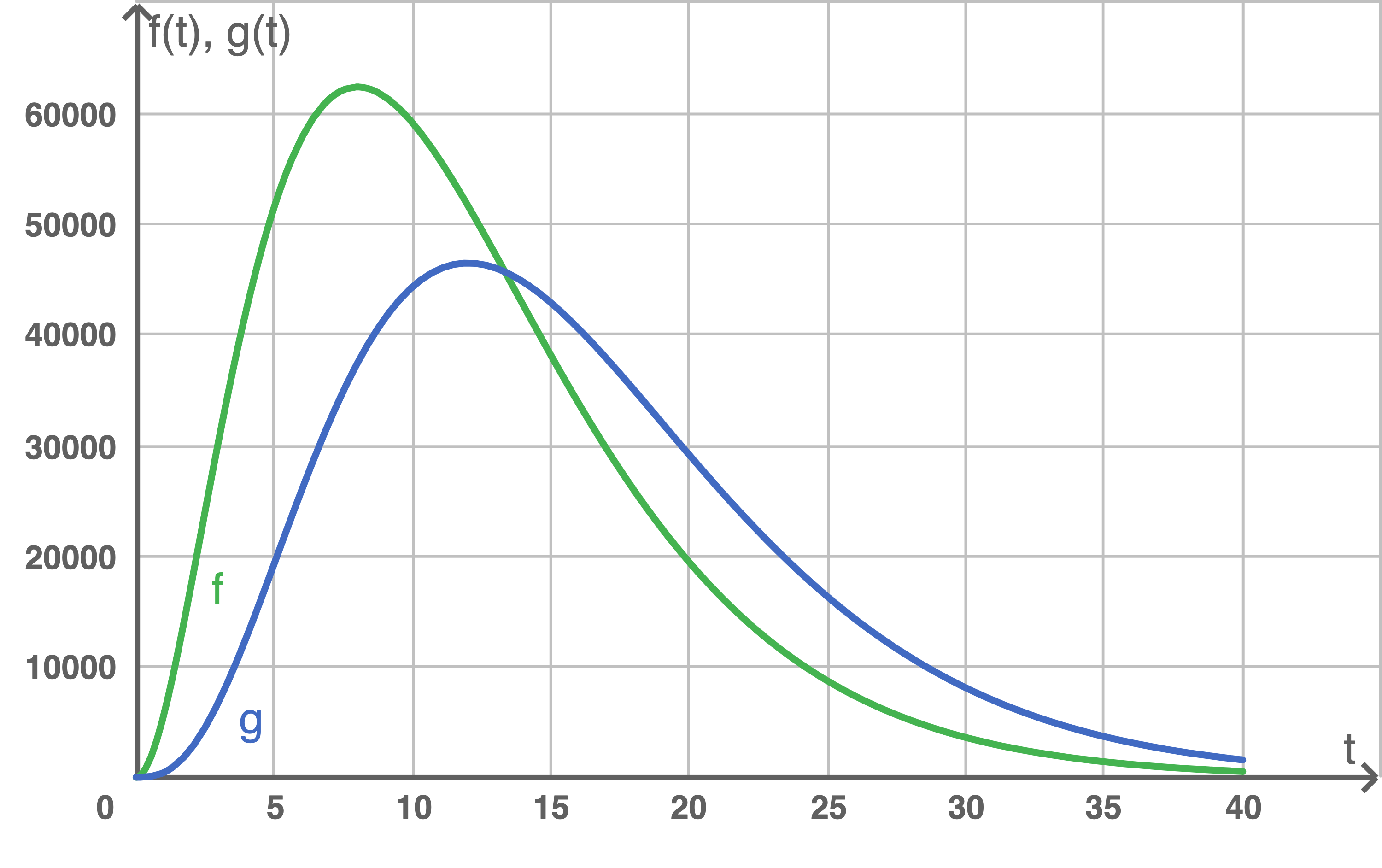 Die Funktion
Die Funktion  ist durch die Gleichung
ist durch die Gleichung  gegeben.
gegeben.

Abbildung 2
(1)
Gib  und
und  an und interpretiere die beiden Werte im Sachzusammenhang.
an und interpretiere die beiden Werte im Sachzusammenhang.
(2)
Ermittle anhand von Abbildung 2 näherungsweise den Zeitpunkt im Beobachtungszeitraum, bis zu dem die Wassermenge im Rückhaltebecken zunimmt und begründe dein Vorgehen.
(3)
Bestimme  und interpretiere das Ergebnis im Sachzusammenhang.
und interpretiere das Ergebnis im Sachzusammenhang.
(5 + 4 + 4 Punkte)
a)
(1)
(2)
Die Zuflussrate soll nach  Stunden maximal sein, das heißt, es muss ein Hochpunkt bestimmt werden:
Anwenden der Produkt- und Kettenregel:
Stunden maximal sein, das heißt, es muss ein Hochpunkt bestimmt werden:
Anwenden der Produkt- und Kettenregel:



![\(\begin{array}[t]{rll}
0&=& 7200 \cdot (-0,25 t^2 +2t) \mathrm e^{-0,25t}&\quad \scriptsize \; \\[5pt]
\end{array}\)](https://mathjax.schullv.de/ed8540c46aa82490744bcccc8a52e0d16d54d70fcd905abd6a436d39314b1b92?color=5a5a5a) Nun kannst du
Nun kannst du  mit dem solve-Befel des TR bestimmen. Es ist
mit dem solve-Befel des TR bestimmen. Es ist  und
und 
Einsetzen der beiden Werte für in die Gleichung, um die passenden
in die Gleichung, um die passenden  -Koordinaten zu erhalten und den gesuchten Hochpunkt zu bestimmen.
-Koordinaten zu erhalten und den gesuchten Hochpunkt zu bestimmen.
 und
und  .
Somit ist der gesuchte Hochpunkt bei
.
Somit ist der gesuchte Hochpunkt bei  . Also
. Also  Stunden nach Beobachtungsbeginn ist die momentane Zuflussrate mit ca.
Stunden nach Beobachtungsbeginn ist die momentane Zuflussrate mit ca.  am größten. Dies passt auch mit dem Graphen der Funktion
am größten. Dies passt auch mit dem Graphen der Funktion  in der Abbildung zusammen.
in der Abbildung zusammen.
Einsetzen der beiden Werte für
b)
Integration mithilfe des TR:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II
 Es fließen ca.
Es fließen ca.  während des gesamten Beobachtungszeitraumes in das Becken.
während des gesamten Beobachtungszeitraumes in das Becken.
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

c)
(1)
Auflösen der Gleichung  nach
nach  mit dem solve-Befehl des TR:
mit dem solve-Befehl des TR:
 .
Das gesuchte Intervall ist folglich
.
Das gesuchte Intervall ist folglich ![\([8,6; \, 16,2]\)](https://mathjax.schullv.de/79cd80197f85b5d8f55fa4284d9f015d49a45bb08f2c241bf79da621878a21b7?color=5a5a5a) .
.
(2)
Bestimmen des gesuchten Wendepunktes von  mithilfe des TR:
mithilfe des TR:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der globale Hochpunkt des Graphen von
Casio Classpad II
Der globale Hochpunkt des Graphen von  hat die Koordinaten
hat die Koordinaten  .
Die momentane Zuflussrate ist folglich nach ca.
.
Die momentane Zuflussrate ist folglich nach ca.  Stunden am größten.
Stunden am größten.
menu  6: Graph analysieren
6: Graph analysieren  3: Maximum
3: Maximum
Analyse  Grafische Lösung
Grafische Lösung  Maximum
Maximum
(3)
Mit dem solve-Befehl des TR ergibt sich:  und
und  . Das heißt, dass bis zum Zeitpunkt
. Das heißt, dass bis zum Zeitpunkt  (nur dieser liegt im Intervall)
(nur dieser liegt im Intervall)  Wasser aus dem Rückhaltebecken fließen.
Wasser aus dem Rückhaltebecken fließen.
d)
(1)
Die Werte lauten:
 und
und 
 Stunden nach Beobachtungsbeginn nimmt die Wassermenge im Rückhaltebecken mit einer Rate von ca.
Stunden nach Beobachtungsbeginn nimmt die Wassermenge im Rückhaltebecken mit einer Rate von ca.  pro Stunde zu. Nach
pro Stunde zu. Nach  Stunden nimmt die Wassermenge mit einer Rate von ca.
Stunden nimmt die Wassermenge mit einer Rate von ca.  pro Stunde ab.
pro Stunde ab.
(2)
Die Wassermenge im Rückhaltebecken nimmt bei  zu, da ab diesem Zeitpunkt der Graph von
zu, da ab diesem Zeitpunkt der Graph von  oberhalb des Graphen von
oberhalb des Graphen von  verläuft. Die momentane Zuflussrate ist größer als die momentane Abflussrate.
verläuft. Die momentane Zuflussrate ist größer als die momentane Abflussrate.
(3)
Lösen des Integrals mit dem TR:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Zum Ende des Beobachtungszeitraumes befinden sich ca.
Casio Classpad II
Zum Ende des Beobachtungszeitraumes befinden sich ca.  Wasser mehr im Becken als zu Beginn.
Wasser mehr im Becken als zu Beginn.
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 
