Aufgabe 1
Die Funktion  ist gegeben durch die Gleichung
ist gegeben durch die Gleichung
 ,
,  .
Der Graph von
.
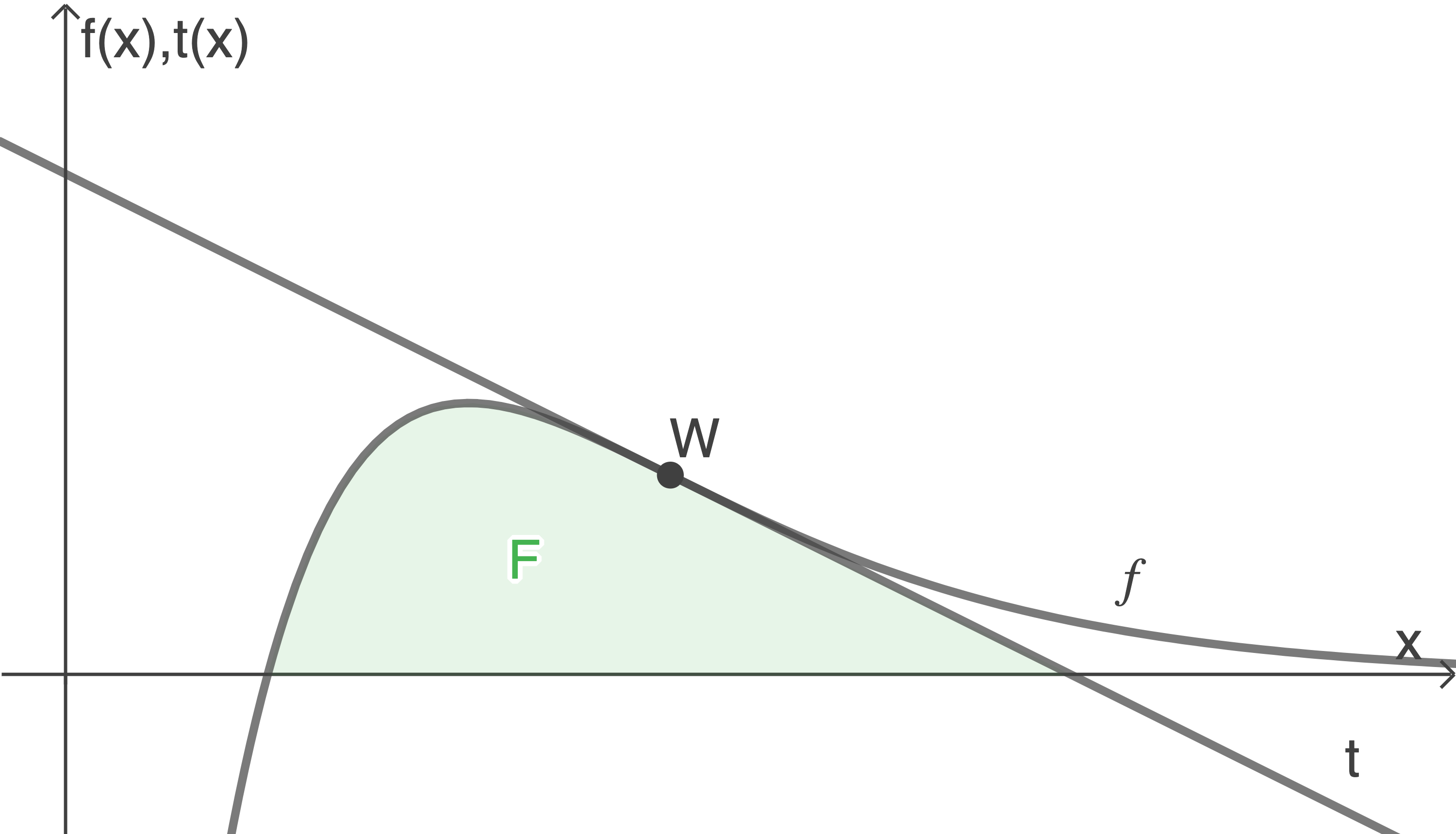
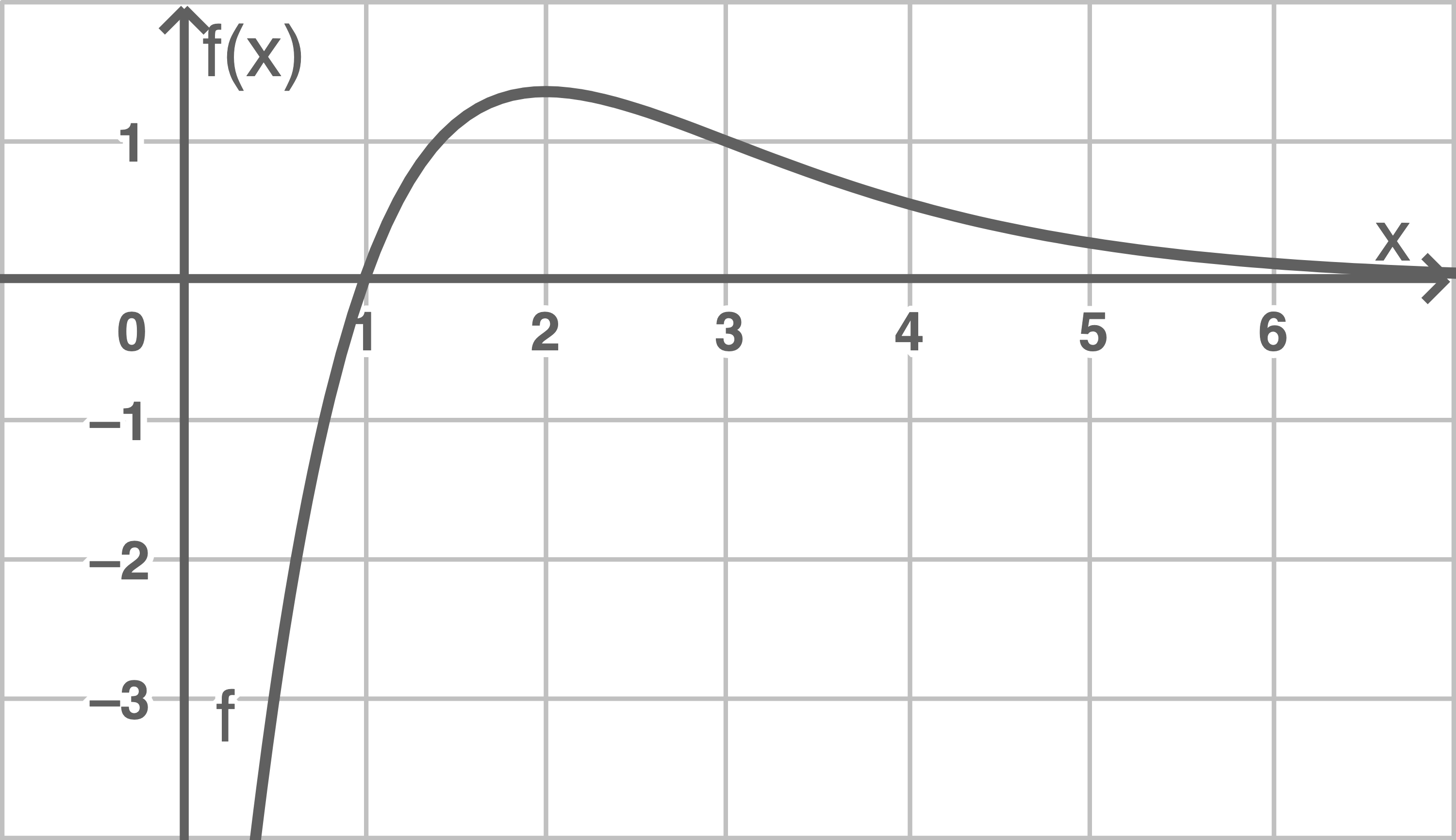
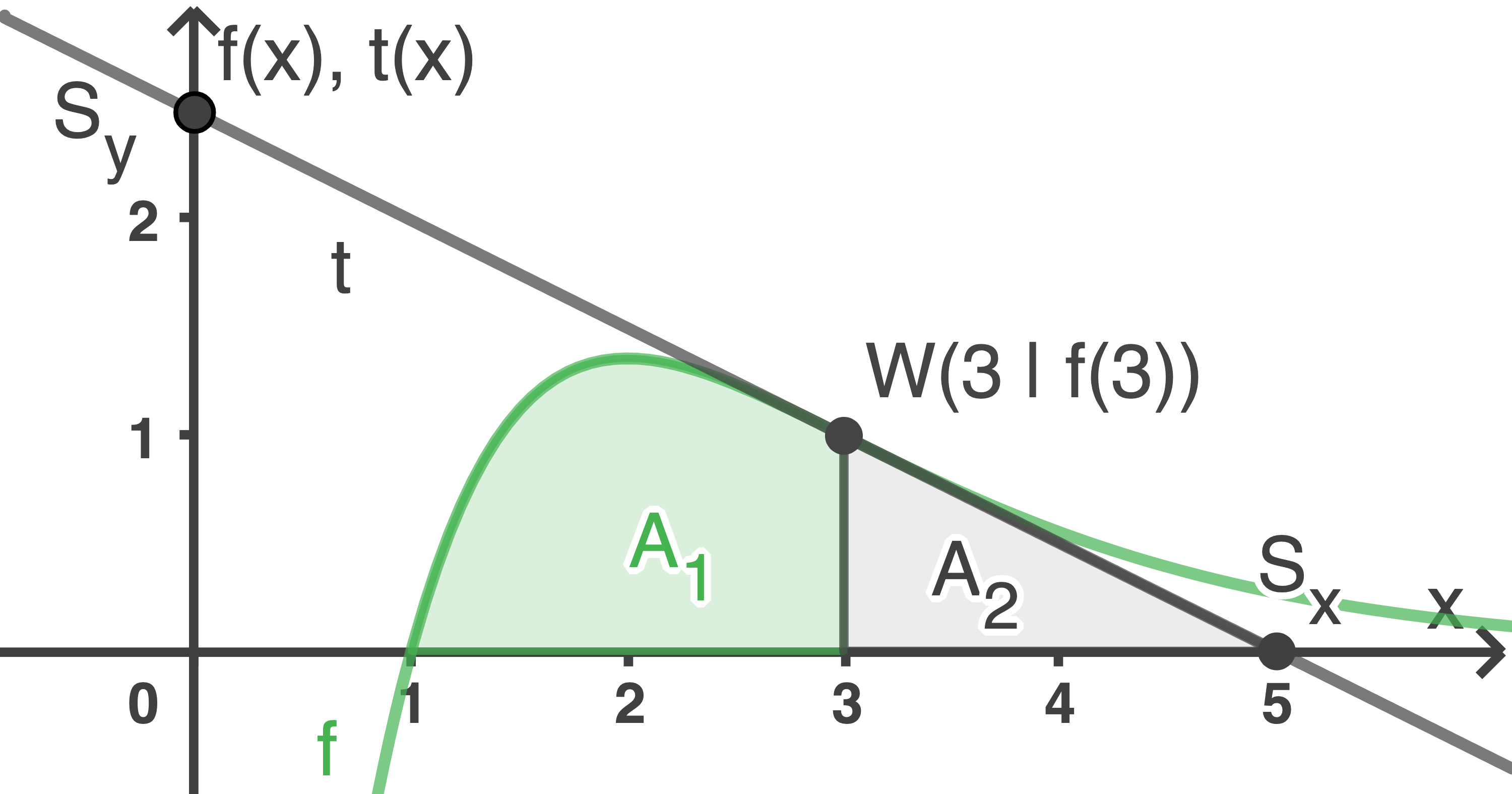
Der Graph von  ist in Abbildung 1 dargestellt.
ist in Abbildung 1 dargestellt.
 ist ein beliebiger Punkt auf dem Graphen von
ist ein beliebiger Punkt auf dem Graphen von 
 legt zusammen mit
legt zusammen mit  und
und  das Dreieck
das Dreieck  fest.
fest.

Abbildung 1
a)
(1)
Begründe, dass  die einzige Nullstelle von
die einzige Nullstelle von  ist.
ist.
(2)
Untersuche  rechnerisch auf lokale Extremstellen.
[Kontrolllösung: An der Stelle
rechnerisch auf lokale Extremstellen.
[Kontrolllösung: An der Stelle  liegt eine lokale Maximalstelle vor.]
liegt eine lokale Maximalstelle vor.]
(3)
Ermittle, für welche  gilt:
gilt: 
(1 + 5 + 4 Punkte)
b)
(1)
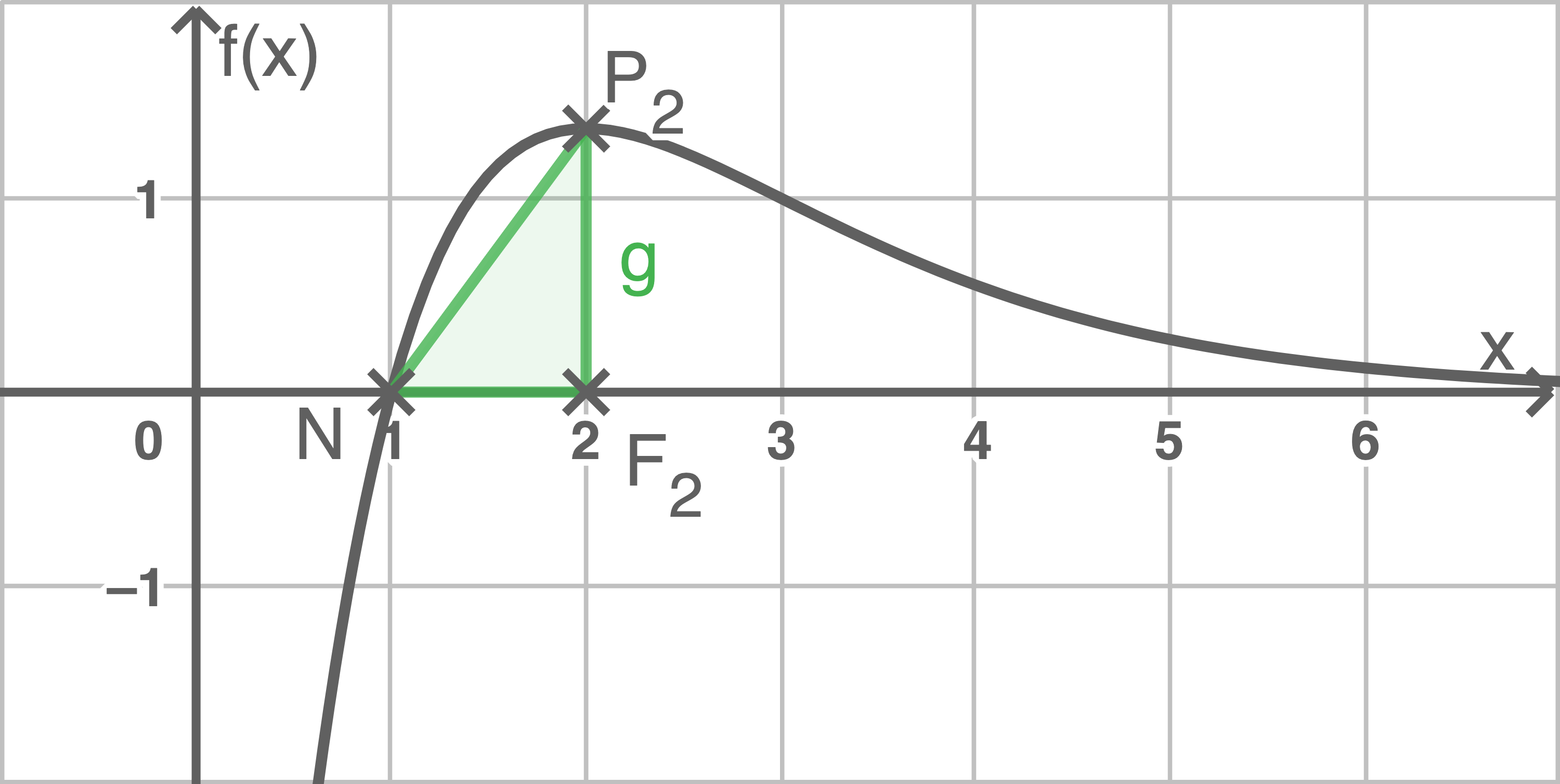
Zeichne in Abbildung 1 das Dreieck  ein, das sich ergibt, wenn
ein, das sich ergibt, wenn  mit dem Hochpunkt von
mit dem Hochpunkt von  übereinstimmt.
übereinstimmt.
(2)
Bestimme den Flächeninhalt des in b) (1) gezeichneten Dreiecks.
(3)
Untersuche, ob  so auf dem Graphen von
so auf dem Graphen von  gewählt werden kann, dass das zugehörige Dreieck
gewählt werden kann, dass das zugehörige Dreieck  den Flächeninhalt
den Flächeninhalt  hat.
hat.
(1 + 2 + 4 Punkte)
c)
(1)
Gegeben ist die Funktion  mit
mit  ,
,  , und der Wendepunkt
, und der Wendepunkt  des Graphen von f.
Weise rechnerisch nach, dass der Graph von
des Graphen von f.
Weise rechnerisch nach, dass der Graph von  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  ist.
ist.
(2)
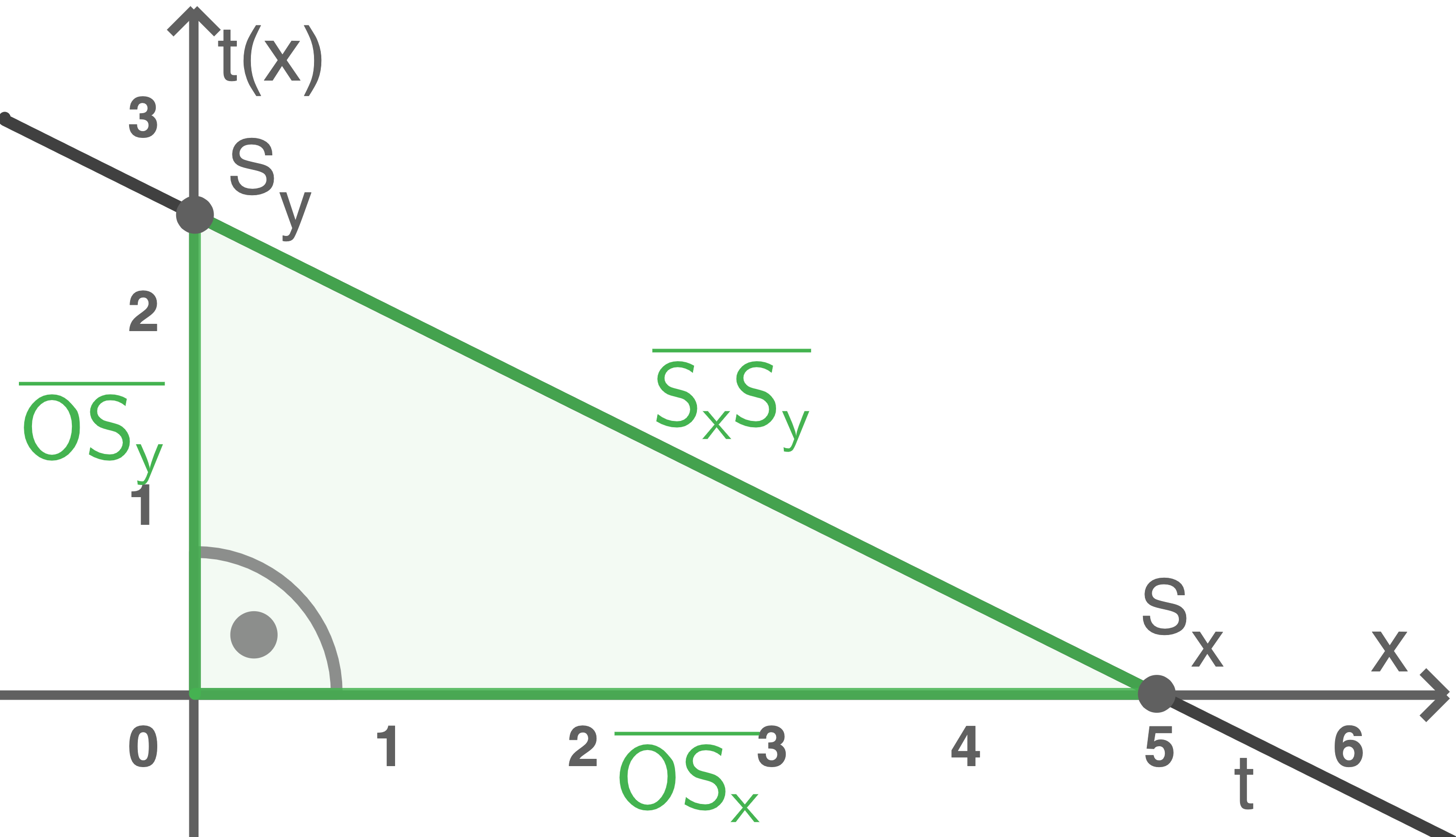
Die Schnittpunkte der in c) (1) gegebenen Tangente mit den beiden Koordinatenachsen legen zusammen mit dem Koordinatenursprung  ein Dreieck fest.
Berechne den Umfang dieses Dreiecks.
ein Dreieck fest.
Berechne den Umfang dieses Dreiecks.
(3)
d)
Die Gerade mit der Gleichung  wird als "1. Winkelhalbierende" bezeichnet. Es gibt genau einen Punkt
wird als "1. Winkelhalbierende" bezeichnet. Es gibt genau einen Punkt  auf dem Graphen von
auf dem Graphen von  in dem die Tangente
in dem die Tangente  an den Graphen von
an den Graphen von  parallel zur 1. Winkelhalbierenden ist.
parallel zur 1. Winkelhalbierenden ist.
(1)
Ermittle rechnerisch eine Gleichung für die Tangente  .
[Mögliche Lösung: Falls man auf vier Stellen nach dem Komma rundet, ergibt sich für die Tangente
.
[Mögliche Lösung: Falls man auf vier Stellen nach dem Komma rundet, ergibt sich für die Tangente  als Gleichung
als Gleichung  .]
.]
(2)
Die Gerade mit der Gleichung  wird als „2. Winkelhalbierende“ bezeichnet.
Bestimme den Schnittpunkt der Tangente
wird als „2. Winkelhalbierende“ bezeichnet.
Bestimme den Schnittpunkt der Tangente  mit der 2. Winkelhalbierenden.
mit der 2. Winkelhalbierenden.
(3)
Ermittle rechnerisch den Abstand, den die Tangente  von der 1. Winkelhalbierenden hat.
von der 1. Winkelhalbierenden hat.
(4 + 2 + 2 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
Für die Nullstelle von  muss gelten:
muss gelten:  . Da der Faktor
. Da der Faktor  ist und auch
ist und auch  ist, folgt
ist, folgt  . Damit ist
. Damit ist  die einzige Nullstelle der Funktion.
die einzige Nullstelle der Funktion.
(2)
1. Schritt: Die ersten beiden Ableitungen bestimmen.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II

 2. Schritt: hinreichendes Kriterium für Extremstellen
2. Schritt: hinreichendes Kriterium für Extremstellen
![\(\begin{array}[t]{rlll}
f](https://mathjax.schullv.de/715a88acf625034c1c51c78204347c92b77f49cec206396492e931c989fe52e7?color=5a5a5a) 3. Schritt: notwendiges Kriterium für Extremstellen
3. Schritt: notwendiges Kriterium für Extremstellen

 An der Stelle
An der Stelle  liegt somit eine lokale Maximalstelle vor.
liegt somit eine lokale Maximalstelle vor.
menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
keyboard  Math2
Math2 

(3)
b)
(1)
Die Extremstelle der Funktion  liegt an
liegt an  daraus folgt
daraus folgt  Daraus ergeben sich die Koordinaten des Hochpunktes mit
Daraus ergeben sich die Koordinaten des Hochpunktes mit  und
und 

(2)
Für den Flächeninhalt der Dreiecksfläche  gilt:
gilt:
![\(\begin{array}[t]{rll}
A_D&=&\dfrac{1}{2} \cdot 1 \cdot f(2) &\quad \scriptsize \\[5pt]
&\approx &\dfrac{1}{2} \cdot 1 \cdot 1,35 &\quad \scriptsize \\[5pt]
&= &0,65 \, [\text{FE}]
\end{array}\)](https://mathjax.schullv.de/613822e74d49808133b766500af0b7a9ca7b9e4a401d6e666172589a24b6cb82?color=5a5a5a)
(3)
Der Flächeninhalt des Dreiecks  ergibt sich mit
ergibt sich mit  Es soll
Es soll  sein. Mit dem solve-Befehl des Taschenrechners folgt die Lösung
sein. Mit dem solve-Befehl des Taschenrechners folgt die Lösung  Für
Für  ergibt sich somit ein Dreieck mit dem Flächeninhalt
ergibt sich somit ein Dreieck mit dem Flächeninhalt 
c)
(1)
1. Schritt: Gleichheit der Steigung prüfen
![\(\begin{array}[t]{rlll}
m_t &=& f](https://mathjax.schullv.de/bb483c1b65bd20d0af5e43f0be42cfd8e272d0ac6fc5083334e2c62f207b06af?color=5a5a5a) 2. Schritt: Punktprobe mit
2. Schritt: Punktprobe mit  Daraus folgt, dass der Graph von
Daraus folgt, dass der Graph von  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  ist.
ist.
(2)
1. Schritt: Schnittpunkte der Tangente mit den Koordinatenachsen bestimmen
Somit folgt der Schnittpunkt mit der  -Achse mit
-Achse mit 
![\(\begin{array}[t]{rll}
t(0)&=& -10\cdot \mathrm e^{-3}\cdot0+50 \cdot \mathrm e^{-3} \\[5pt]
&=&50 \cdot \mathrm e^{-3}
\end{array}\)](https://mathjax.schullv.de/141c19e33759f989664d2385fb8fa71ad3e66598ad223f8cd996a5590894a157?color=5a5a5a) Der Schnittpunkt der Tangente mit der
Der Schnittpunkt der Tangente mit der  -Achse ist
-Achse ist  2. Schritt: Länge der Strecke zwischen den Schnittpunkten bestimmen
2. Schritt: Länge der Strecke zwischen den Schnittpunkten bestimmen
![\(\begin{array}[t]{rlll}
\mid \overline{S_xS_y}\mid^2 &=& 5^2+(50 \cdot \mathrm e^{-3})^2& \quad \scriptsize \mid \; \sqrt{\;}\\[5pt]
\mid \overline{S_xS_y}\mid &=& \sqrt{ 5^2+ (50 \cdot \mathrm e^{-3})^2}\\[5pt]
&\approx& 5,59& \quad \scriptsize\\[5pt]
\end{array}\)](https://mathjax.schullv.de/1983598d188587d3a95b439d0ab3a1d88e57fedfa08e95649490f2f2bd3675a6?color=5a5a5a) Die Länge der Strecke zwischen den Schnittpunkten der Tangente mit den Koordinatenachsen beträgt ungefähr
Die Länge der Strecke zwischen den Schnittpunkten der Tangente mit den Koordinatenachsen beträgt ungefähr ![\(5,59 \; [\text{LE}].\)](https://mathjax.schullv.de/6122f7d176e562d38daaaa66beecae92a428845aca1b7f46d25df0c6bfc91d5d?color=5a5a5a) 3. Schritt: Umfang des Dreiecks berechnen
3. Schritt: Umfang des Dreiecks berechnen
![\(U= 5+2,49 +5,59 = 13,08 \,[\text{LE}]\)](https://mathjax.schullv.de/fb11d29e23170136063c61d4133449ef4fac596825274ecdfa36dbfd48ec6d54?color=5a5a5a)
Die Länge der Strecke zwischen den Schnittpunkten wird mit dem Satz des Pythagoras bestimmt, da  ein rechtwinkliges Dreieck mit der Hypotenuse
ein rechtwinkliges Dreieck mit der Hypotenuse  ist.
ist.

(3)
Für den Inhalt der Fläche  gilt:
gilt: 


Die Werte von
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

d)
(1)
Die allgemeine Tangentengleichung lautet:  Da die Tangente
Da die Tangente  parallel zur 1. Winkelhalbierenden ist, gilt folglich
parallel zur 1. Winkelhalbierenden ist, gilt folglich 
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/a3483546c4fd03ea575928a69a32c5811f9310ea3a81095b7d2ecf4ac06c2d72?color=5a5a5a)
![\(\begin{array}[t]{rll}
f(x_0)&=&f(1,5356) &\quad \scriptsize \\[5pt]
&=&1,1533
\end{array}\)](https://mathjax.schullv.de/5c9700f34652c8a7c1a244874e18ca0a637a69959664143a0d42c9770e63f0e2?color=5a5a5a) Eingesetzt in die Tangentengleichung ergibt sich:
Eingesetzt in die Tangentengleichung ergibt sich:
![\(\begin{array}[t]{rll}
t_R (x)&=&1 \cdot (x-1,5356) +1,1533 &\quad \scriptsize \\[5pt]
t_R (x)&=&x-0,3823
\end{array}\)](https://mathjax.schullv.de/7327078277461860a64e7a38de00cff687589b38ac3bb1ceb45fd898d231da86?color=5a5a5a)
(2)
Die Koordinaten des Schnittpunktes zwischen  und
und  werden durch Gleichsetzen, Auflösen nach
werden durch Gleichsetzen, Auflösen nach  und Einsetzen in eine der beiden Gleichungen berechnet.
und Einsetzen in eine der beiden Gleichungen berechnet.
![\(\begin{array}[t]{rll}
t_R (x)&=& y&\quad \scriptsize \\[5pt]
x-0,3823 &=& -x&\quad \scriptsize \mid\; -x \\[5pt]
-0,3823 &=& -2x&\quad \scriptsize \mid\; :(-2) \\[5pt]
0,1912&\approx &x
\end{array}\)](https://mathjax.schullv.de/c9a5807ba8aee05c46420c55dbee985029e1b6cc3a15b890af645256b45b1ad8?color=5a5a5a)



 Die Koordinaten des Schnittpunkts der Tangente
Die Koordinaten des Schnittpunkts der Tangente  und der 2.Winkelhalbierenden lauten
und der 2.Winkelhalbierenden lauten 
(3)
1. Nullstelle der Winkelhalbierenden bestimmen
Die Funktion der Winkelhalbierenden sei im folgendem  .
.
![\(\begin{array}[t]{rll}
w(x) &=& 0& \quad \scriptsize \\[5pt]
0 &=& x& \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/635ca978db8227e69d83976fd8994aee6e9253fb5548fe0bdfdb15e03b0401f2?color=5a5a5a) 2. Nullstelle von
2. Nullstelle von  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
t_R(0) &=& 0& \quad \scriptsize \\[5pt]
0 &=& x-0,3824& \quad \scriptsize \mid +0,3824 \\[5pt]
x &=& 0,3824& \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f7aebe250f15cb7f2ef07e42c700d87277858fab4c6782554508e9afac87164e?color=5a5a5a) 3. Abstand der Nullstellen bestimmen
Der Abstand zwischen den Nullstellen beträgt
3. Abstand der Nullstellen bestimmen
Der Abstand zwischen den Nullstellen beträgt



![\(=0,3824 \, [\text{LE}].\)](https://mathjax.schullv.de/1f421a047b666d448f0eea087df07ba12663ef0e167d881a28f5b18d02c83d25?color=5a5a5a) 4. Abstand
4. Abstand  zwischen den Geraden bestimmen
zwischen den Geraden bestimmen
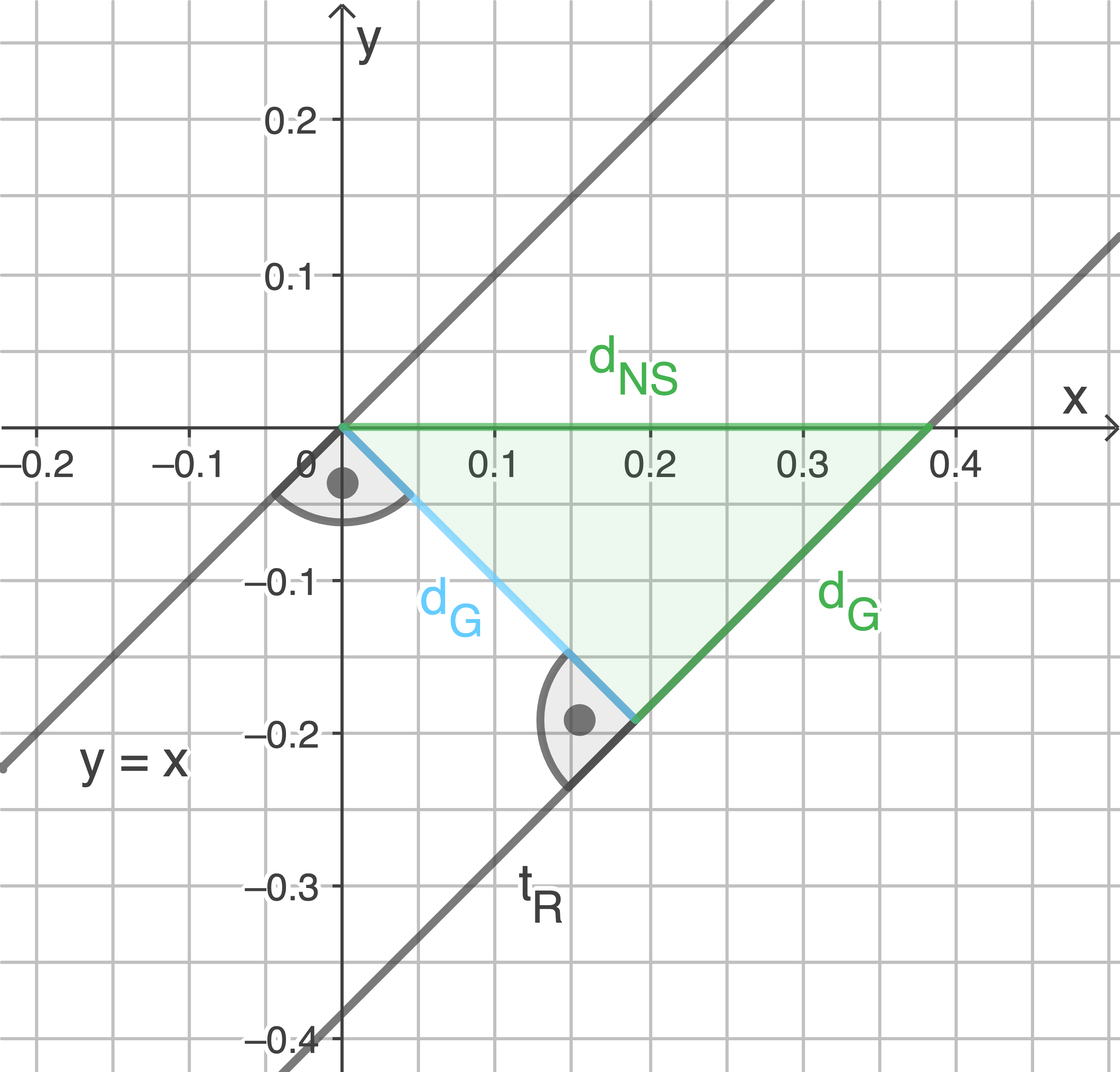
 wird mit dem Satz des Pythagoras berechnet, denn in dem grünen rechtwinkligen Dreieck gilt:
wird mit dem Satz des Pythagoras berechnet, denn in dem grünen rechtwinkligen Dreieck gilt:
![\(\begin{array}[t]{rll}
d_{NS}^2&=& d_G^2 +d_G^2&\quad \scriptsize \\[5pt]
0,3824^2&=& 2 \cdot d_G^2 &\quad \scriptsize \mid\;:2 \, \mid\sqrt{\,} \\[5pt]
\dfrac{0,3824}{\sqrt{2}}&=& d_G &\quad \scriptsize \\[5pt]
0,2704 \, [\text{LE}]&\approx&d_G
\end{array}\)](https://mathjax.schullv.de/74e44e72c17000d7efcb9d9602277169eb383254b005f29956f090006d2de5be?color=5a5a5a)