Lerninhalte in Mathe

Abi-Aufgaben GK (GTR)

Abi-Aufgaben GK (CAS)

Digitales Schulbuch

Inhaltsverzeichnis

Aufgabe 3

Die Abbildung zeigt den Würfel $ABCDEFGH$ mit $G(5\mid 5\mid 5)$ und $H(0\mid 5\mid 5)$ in einem kartesischen Koordinatensystem.
Die Punkte $I(5\mid 0\mid 1)$ , $J(2\mid 5\mid 0)$ , $K(0\mid 5\mid 2)$ und $L(1\mid 0\mid 5)$ liegen jeweils auf einer Kante des Würfels.

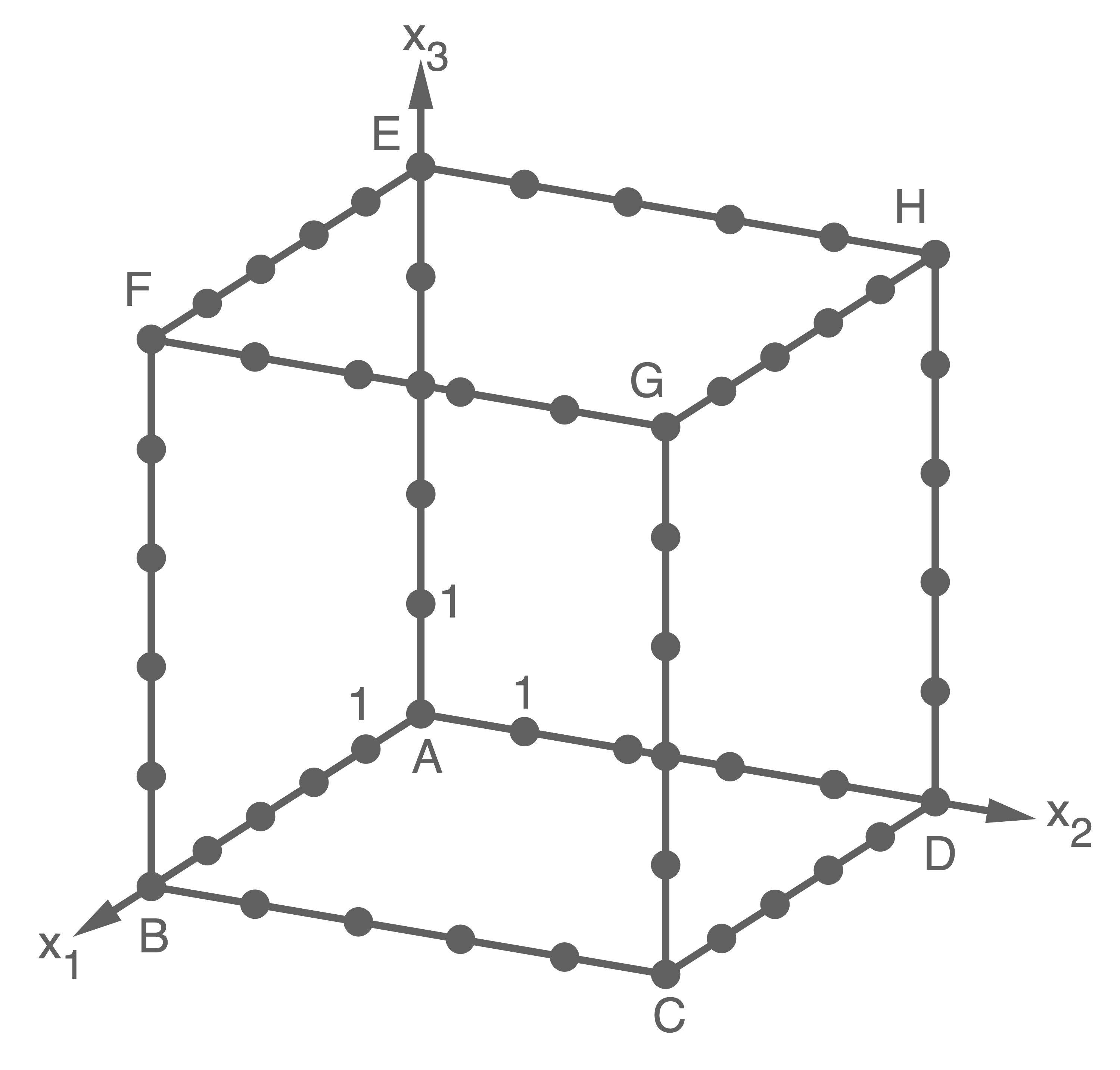
Abbildung

Abbildung

a)

Gib die Koordinaten der Eckpunkte $D$ und $F$ an.

(2 Punkte)

b)

Zeichne das Viereck $IJKL$ in die Abbildung ein.

(4 Punkte)

c)

Das Viereck $IJKL$ liegt in einer Ebene $Q.$
Stelle eine Parametergleichung der Ebene $Q$ auf.

[Mögliche Lösung: $Q:\, \overrightarrow{x} =$ $\pmatrix{-2\\5\\4} + k\cdot \pmatrix{-5\\5\\1} + l\cdot \pmatrix{-6\\5\\2}$ mit $k,l\in \mathbb{R}$ ]

(4 Punkte)

d)

Stelle die Raumdiagonale $\overline{AG}$ in Parameterform dar.
Berechne den Schnittpunkt $U$ von $\overline{AG}$ und der Ebene $Q.$

(7 Punkte)

e)

Zeige, dass das Viereck $IJKL$ ein Trapez ist, in dem zwei Seiten gleich lang sind.
Weise nach, dass die Seite $\overline {IL}$ des Trapezes doppelt so lang ist wie die Seite $\overline {JK}.$

(6 Punkte)

f)

Berechne die Größe eines Innenwinkels des Trapezes $IJKL.$

(4 Punkte)

g)

Der Punkt $P(4\mid 0\mid 2)$ liegt auf der Strecke $\overline{IL}.$
Zeige, dass $\overrightarrow{JP}$ senkrecht auf $\overrightarrow{IL}$ steht.

(3 Punkte)

h)

Berechne den Flächeninhalt des Trapezes $IJKL.$

(5 Punkte)

i)

Gegeben ist die Ebene $S:\, \overrightarrow{x} = v\cdot \pmatrix{-1\\-5\\5} + w\cdot \pmatrix{-5\\5\\1}$ mit $v,w\in \mathbb{R}.$

Der Punkt $K$ liegt in einer Ebene $T$ , die parallel zu $S$ ist.
Untersuche, ob auch der Punkt $L$ in $T$ liegt.

(5 Punkte)

a)

$\blacktriangleright$ Koordinaten der Eckpunkte angeben

Anhand der Koordinaten von $G$ und $H$ kannst du erkennen, dass die Kantenlänge des Würfels $5\,\text{LE}$ ist. Es ergibt sich:

$D(0\mid 5\mid 0)$ und $F(5\mid 0\mid 5).$

b)

$\blacktriangleright$ Viereck einzeichnen

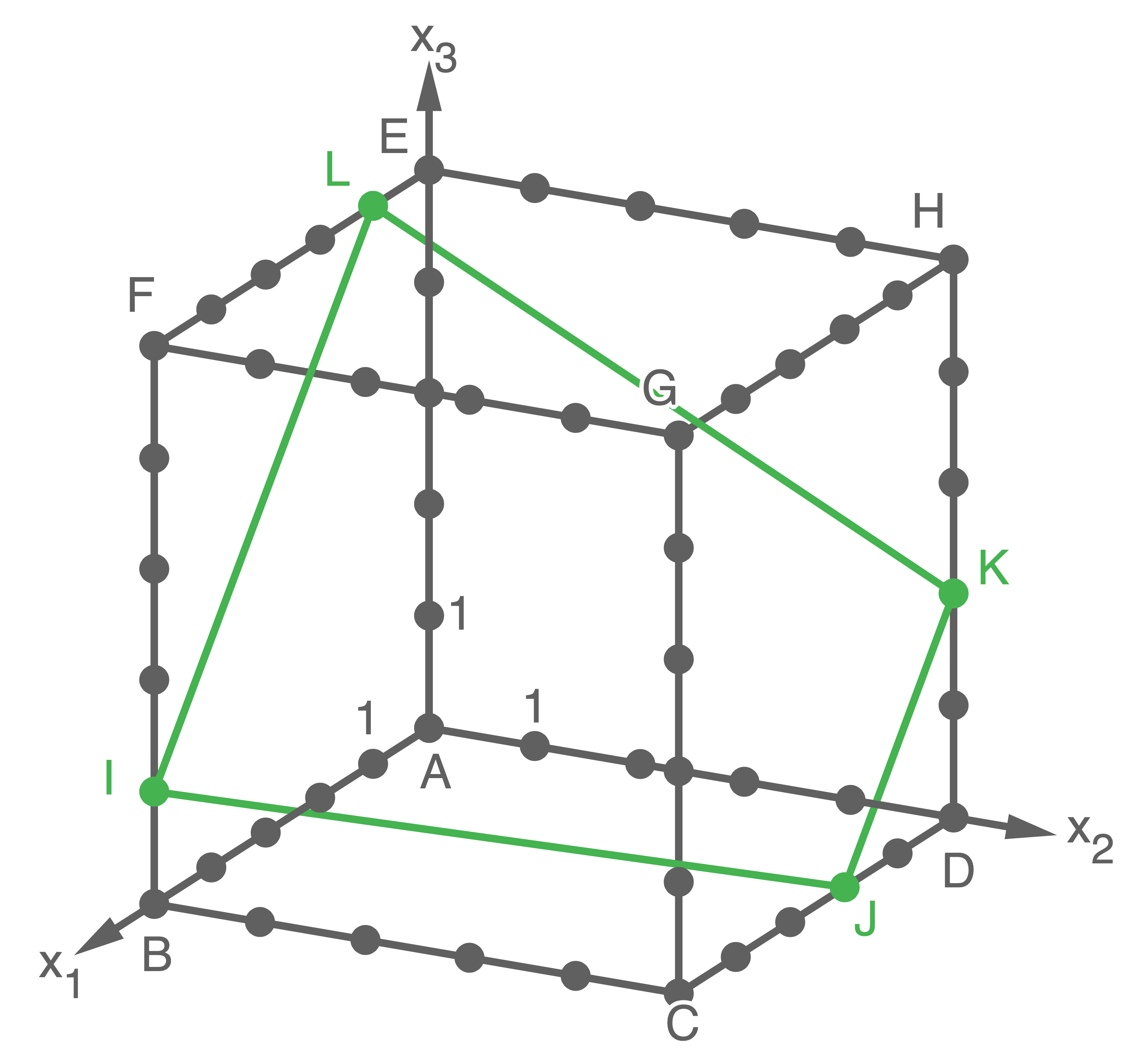
Viereck eingezeichnet

c)

$\blacktriangleright$ Parametergleichung aufstellen

Mit den Koordinaten von $I,$ $J,$ $K$ und $L$ erhältst du beispielsweise:

$Q:\, \overrightarrow{x} = ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

mit $k,l\in \mathbb{R}.$

d)

$\blacktriangleright$ Raumdiagonale in Parameterform darstellen

$\overline{AG}:\, \overrightarrow{x}=t\cdot \pmatrix{5\\5\\5}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

mit $t\in [0;1]$ beschreibt die Raumdiagonale $\overline{AG}.$

$\blacktriangleright$ Schnittpunkt berechnen

$\pmatrix{2\\-5\\-4}=...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Daraus erhält man folgendes Gleichungssystem:

$l=3-10t$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Setze $\text{I}‘$ in $\text{II}‘$ ein:

$t=\frac{3}{7}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Einsetzen in $\text{I}‘$ liefert:

$\begin{array}[t]{rll} \text{I}‘\quad l&=& 3-10\cdot \frac{3}{7} \\[5pt] &=& -\frac{9}{7} \\[5pt] \end{array}$

Einsetzen in $\text{III}:$

$k=\frac{5}{7}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Einsetzen von $t= \frac{3}{7}$ in die Parametergleichung der Raumdiagonale:

$\overrightarrow{OU} = \pmatrix{\frac{15}{7} \\\frac{15}{7}\\\frac{15}{7} }$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Koordinaten des Schnittpunkts von $\overline{AG}$ und $Q$ lauten $U\left( \frac{15}{7} \mid \frac{15}{7}\mid \frac{15}{7}\right).$

e)

$\blacktriangleright$ Trapezform mit zwei gleich langen Seiten zeigen

In der Abbildung von oben kannst du erkennen, dass die beiden parallelen Seiten des Trapezes vermutlich die beiden Seiten $\overline{LI}$ und $\overline{KJ}$ sind. Für die zugehörigen Verbindungsvektoren folgt:

$\begin{array}[t]{rll} \overrightarrow{LI} &=& \pmatrix{4\\0\\-4} \\[5pt] \overrightarrow{KJ} &=& \pmatrix{2\\0\\-2} \end{array}$

Es gilt $\overrightarrow{LI} = 2\cdot \overrightarrow{KJ}.$ Die beiden Vektoren $\overrightarrow{LI}$ und $\overrightarrow{KJ}$ sind also linear abhängig und damit parallel zueinander. Daher sind auch die zugehörigen Vierecksseiten $\overline{LI}$ und $\overline{KJ}$ parallel zueinander. Es handelt sich bei dem Viereck $IJKL$ daher um ein Trapez.
Gefordert ist nun noch zu zeigen, dass die beiden anderen gegenüberliegenden Seiten gleich lang sind. Die Länge der Seiten $\overline{LK}$ und $\overline{IJ}$ kannst du mithilfe des Vektorbetrags berechnen.

$\begin{array}[t]{rll} \overline{LK}&= \sqrt{35} \\[10pt] \overline{IJ}&= \sqrt{35} \\[10pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Es ist also $\overline{LK} = \overline{IJ}.$ Die beiden gegenüberliegenden Seiten $\overline{LK}$ und $\overline{IJ}$ sind also gleich lang. Das Viereck $IJKL$ ist also ein Trapez, bei dem zwei gegenüberliegende Seiten gleich lang sind.

$\blacktriangleright$ Doppelte Länge nachweisen

Berechne die beiden Längen mithilfe des Vektorbetrags:

$\begin{array}[t]{rll} \overline{IL}&=& \sqrt{32} \\[10pt] \overline{JK} &=& \sqrt{8} \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Vergleiche nun:

$\begin{array}[t]{rll} \overline{IL} &=& \sqrt{32} \\[5pt] &=& \sqrt{8\cdot 4}\\[5pt] &=& \sqrt{8}\cdot \sqrt{4} \\[5pt] &=& 2\cdot \sqrt{8} \\[5pt] &=& 2\cdot \overline{JK} \\[5pt] \end{array}$

Die Strecke $\overline{IL}$ ist also doppelt so lang wie die Strecke $\overline{JK}.$

f)

$\blacktriangleright$ Größe eines Innenwinkels berechnen

Die Größe eines Innenwinkels kannst du über den Schnittwinkel der zugehörigen Vektoren berechnen. Berechne beispielsweise den Winkel zwischen $\overrightarrow{LI}$ und $\overrightarrow{LK}$ mit der zugehörigen Formel:

$\alpha \approx 76,17^{\circ}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Innenwinkel des Trapezes im Punkt $L$ ist ca. $76,17^{\circ}$ groß.

g)

$\blacktriangleright$ Orhtogonalität zeigen

$\overrightarrow{IL} = \pmatrix{-4\\0\\4},$ $\overrightarrow{JP} = \pmatrix{2\\-5\\2}$

$\overrightarrow{JP}\circ\overrightarrow{IL} = 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Da das Skalarprodukt der beiden Vektoren $\overrightarrow{IL}$ und $\overrightarrow{JP}$ Null ist, stehen die beiden Vektoren senkrecht aufeinander.

h)

$\blacktriangleright$ Flächeninhalt des Trapezes bestimmen

Da $\overrightarrow{JP}$ senkrecht auf $\overrightarrow{IL}$ steht, beschreibt $\left|\overrightarrow{JP} \right|$ die Höhe des Trapezes.

$\begin{array}[t]{rll} \left|\overrightarrow{JP} \right|&=& \sqrt{33} \\[10pt] \left|\overrightarrow{IL} \right| &=& \sqrt{32} \\[10pt] \left|\overrightarrow{KJ} \right| &=& \sqrt{8} \\[10pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Für den Flächeninhalt ergibt sich:

$A=3\sqrt{66}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Flächeninhalt des Trapezes beträgt $3\cdot \sqrt{66}\,\text{FE}.$

i)

$\blacktriangleright$ Lage untersuchen

1. Schritt: Ebenengleichung für $T$ aufstellen

Da $T$ parallel zu $S$ verläuft, kannst du die Spannvektoren von $S$ aus der Ebenengleichung von $S$ ablesen und für $T$ verwenden:

$\overrightarrow{r_1} = \pmatrix{-1\\-5\\5},$ $\overrightarrow{r_2} = \pmatrix{-5\\5\\1}$

Du kannst $K$ als Stützpunkt verwenden und erhältst:

$T:\, \overrightarrow{x} = ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

2. Schritt: Lage des Punkts überprüfen

Setze nun die Koordinaten von $L$ in die Ebenengleichung von $T$ ein, um zu überprüfen, ob $L$ in $T$ liegt:

$\pmatrix{1\\-5\\3} = ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Daraus erhältst du folgendes Gleichungssystem:

$j=-\frac{1}{3}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Einsetzen in die erste Gleichung liefert:

$i=\frac{2}{3}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Überprüfe noch die zweite und die dritte Gleichung:

$\begin{array}[t]{rll} \text{II}\quad & -5 &=& -5 \\[10pt] \text{III}\quad & 3 &=& 3 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Da das Gleichungssystem eine eindeutige Lösung besitzt, erfüllen die Koordinaten von $L$ die Ebenengleichung von $T.$ Der Punkt $L$ liegt also in $T.$

Bildnachweise [nach oben]

[1]

© - SchulLV.