Aufgabe 2
Das Jagdverhalten von Raubkatzen in der freien Wildbahn ist gekennzeichnet durch eine hohe Anfangsbeschleunigung. Darauf folgt eine kurze Phase mit annähernd konstanter Geschwindigkeit, bevor die Geschwindigkeit wieder abfällt.
Die Geschwindigkeit eines Tigers bei einem Jagdvorgang aus der Ruheposition heraus wird für zunächst ohne Berücksichtigung der Phase mit konstanter Geschwindigkeit modelliert. Dazu wird für
zunächst ohne Berücksichtigung der Phase mit konstanter Geschwindigkeit modelliert. Dazu wird für  die Funktion
die Funktion  mit
mit

 verwendet. Dabei gibt
verwendet. Dabei gibt  die Zeit seit Verlassen der Ruheposition in Sekunden und
die Zeit seit Verlassen der Ruheposition in Sekunden und  die Geschwindigkeit in
die Geschwindigkeit in  an.
an.
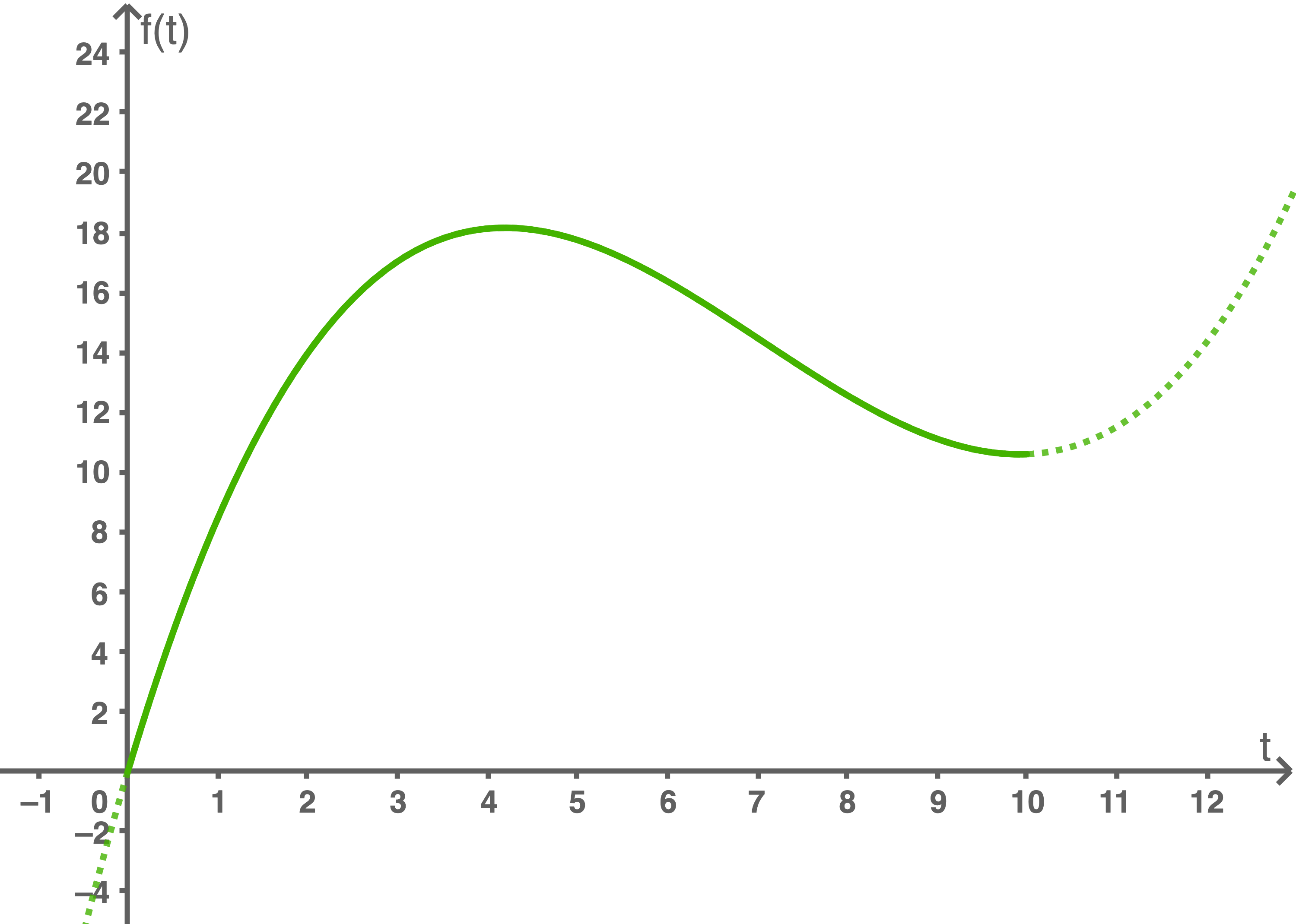
Die Geschwindigkeit eines Tigers bei einem Jagdvorgang aus der Ruheposition heraus wird für

Abbildung 1
a)
(1)
Gib den Funktionswert von  für
für  an und interpretiere diesen Wert im Sachzusammenhang.
an und interpretiere diesen Wert im Sachzusammenhang.
(2)
Weise rechnerisch nach, dass der Tiger seine Maximalgeschwindigkeit von ca.  ungefähr
ungefähr  Sekunden nach Verlassen der Ruheposition erreicht, und gib die Maximalgeschwindigkeit in
Sekunden nach Verlassen der Ruheposition erreicht, und gib die Maximalgeschwindigkeit in  an.
an.
(3)
Ermittle das Zeitintervall, in dem die Geschwindigkeit des Tigers mindestens  beträgt.
beträgt.
(3 + 7 + 4 Punkte)
b)
(1)
Erläutere die Bedeutung der ersten Ableitung von  im Sachzusammenhang.
im Sachzusammenhang.
(2)
Ermittle den Zeitpunkt, zu dem die Geschwindigkeit am stärksten abnimmt, auf zwei Nachkommastellen genau.
(2 + 4 Punkte)
c)
Bestimme  und erläutere die Bedeutung dieses Wertes im Sachzusammenhang.
und erläutere die Bedeutung dieses Wertes im Sachzusammenhang.
(4 Punkte)
d)
Nimm an, dass der Tiger zunächst seine Maximalgeschwindigkeit gemäß dem oberen Modell erreicht (Phase 1). Nach Erreichen seiner Maximalgeschwindigkeit behält er diese noch  lang bei (Phase 2). Anschließend verringert sich seine Geschwindigkeit gemäß einem neuen Modell (Phase 3). Dieses entspricht bis auf eine zeitliche Verschiebung dem oberen Modell (vgl. Abbildung 2). Ab
lang bei (Phase 2). Anschließend verringert sich seine Geschwindigkeit gemäß einem neuen Modell (Phase 3). Dieses entspricht bis auf eine zeitliche Verschiebung dem oberen Modell (vgl. Abbildung 2). Ab  läuft er mit konstanter Geschwindigkeit weiter (Phase 4). Im Folgenden werden die ersten
läuft er mit konstanter Geschwindigkeit weiter (Phase 4). Im Folgenden werden die ersten  (Phase 1 bis 3) dieses Ablaufs betrachtet.
(Phase 1 bis 3) dieses Ablaufs betrachtet.
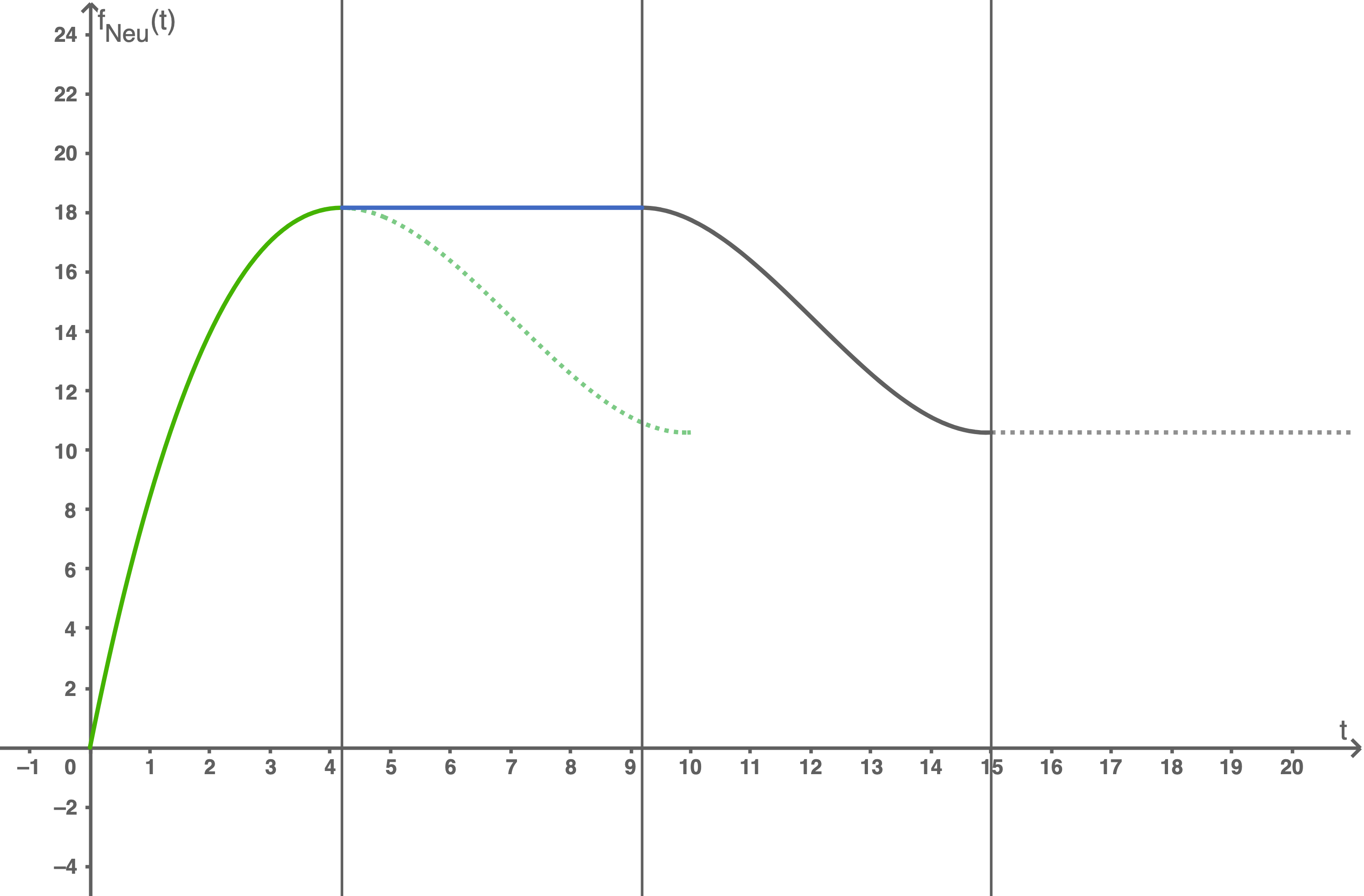

Abbildung 2
(1)
Gib für die Phasen 2 und 3 jeweils einen Funktionsterm an.
[Hinweis: Der Term für Phase 3 muss nicht vereinfacht werden.]
[Hinweis: Der Term für Phase 3 muss nicht vereinfacht werden.]
(2)
Prüfe, ob nach  ein knickfreier Übergang zu einer konstanten Funktion, welche die Geschwindigkeit in Phase 4 modelliert, möglich ist.
ein knickfreier Übergang zu einer konstanten Funktion, welche die Geschwindigkeit in Phase 4 modelliert, möglich ist.
(3)
Ermittle die Länge der Strecke, die der Tiger in diesen ersten  zurücklegt, und gib die Durchschnittsgeschwindigkeit in diesem Zeitintervall an.
zurücklegt, und gib die Durchschnittsgeschwindigkeit in diesem Zeitintervall an.
(4+3+5 Punkte)
e)
Für eine andere Raubkatze wird ein Modell gesucht, bei dem die Höchstgeschwindigkeit  nach dem Verlassen der Ruhelage erreicht wird und
nach dem Verlassen der Ruhelage erreicht wird und  beträgt. Dieses Modell soll durch die Funktion
beträgt. Dieses Modell soll durch die Funktion  mit
mit
 mit
mit  beschrieben werden.
beschrieben werden.
Ermittle geeignete Werte für die beiden Parameter und
und  , sodass die Funktion
, sodass die Funktion  als Transformation der Funktion
als Transformation der Funktion  die beschriebene Eigenschaft hat.
[Hinweis: Die neue Funktionsvorschrift muss nicht vereinfacht werden.]
die beschriebene Eigenschaft hat.
[Hinweis: Die neue Funktionsvorschrift muss nicht vereinfacht werden.]
Ermittle geeignete Werte für die beiden Parameter
(4 Punkte)
a)
(1)
Einsetzen von  in die Funktionsgleichung:
in die Funktionsgleichung:  .
.
Der Tiger hat nach eine Geschwindigkeit von
eine Geschwindigkeit von  .
.
Der Tiger hat nach
(2)
Die Maximalgeschwindigkeit kann über das Maximum ermittelt werden.
Die Ableitungsfunktion lautet :  Nullstellen für
Nullstellen für  liefert der GTR im Intervall
liefert der GTR im Intervall ![\([0,10]\)](https://mathjax.schullv.de/f0a5fc7603ec6f5bf5258572dec467de75f1bfab1842d819880219d4f6b95590?color=5a5a5a) bei
bei  und
und  .
Die zugehörigen Funktionswerte lauten:
.
Die zugehörigen Funktionswerte lauten:  und
und  . Das Maximum könnte jedoch auch am Rand angenommen werden. Wegen
. Das Maximum könnte jedoch auch am Rand angenommen werden. Wegen  und
und  ist dies jedoch ausgeschlossen.
ist dies jedoch ausgeschlossen.
Der Tiger hat somit nach ca seine Höchstgeschwindigkeit
seine Höchstgeschwindigkeit  erreicht.
erreicht.
Der Tiger hat somit nach ca
b)
(1)
Die erste Ableitung  entspricht der momentanen Änderungsrate. Sie gibt die momentane Beschleunigung des Tigers nach seinem Start aus der Ruhe an.
entspricht der momentanen Änderungsrate. Sie gibt die momentane Beschleunigung des Tigers nach seinem Start aus der Ruhe an.
(2)
Die Stelle, an der die Geschwindigkeit am stärksten abnimmt, ist das Minimum der Ableitungsfunktion.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Die zu
Casio Classpad II
Die zu  gehörende Parabel hat ihr Minimum an der Stelle
gehörende Parabel hat ihr Minimum an der Stelle  welche somit auch der Zeitpunkt ist, an dem die Geschwindigkeit des Tigers am stärksten abnimmt.
welche somit auch der Zeitpunkt ist, an dem die Geschwindigkeit des Tigers am stärksten abnimmt.
menu  6: Graph analysieren
6: Graph analysieren  2: Minimum
2: Minimum
Analyse  Grafische Lösung
Grafische Lösung  Minimum
Minimum
c)
(1)
Es gilt:

 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II

 Der Tiger legt somit einen Weg von
Der Tiger legt somit einen Weg von  innerhalb von
innerhalb von  zurück.
zurück.
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

d)
(1)
Die Phasen befinden sich auf den folgenden Intervallen:
Phase 2: ![\([4,2; 9,2]\)](https://mathjax.schullv.de/f5a08667a1d43bfdf3e4ba68be0c4a923ced76749b483fe24fa1062b9c89af17?color=5a5a5a) und Phase 3:
und Phase 3: ![\([9,2; 15]\)](https://mathjax.schullv.de/e124455048fa2a0c60960cddea8a2c3703598d88dc99e680156ee5fef3434289?color=5a5a5a) .
In Phase 2 läuft der Tiger mit seiner Maximalgeschwindigkeit
.
In Phase 2 läuft der Tiger mit seiner Maximalgeschwindigkeit  Die Höchstgeschwindigkeit beträgt
Die Höchstgeschwindigkeit beträgt  .
Phase 3 entspricht dem Graphen von Abbildung 1 im Intervall
.
Phase 3 entspricht dem Graphen von Abbildung 1 im Intervall ![\([5,10]\)](https://mathjax.schullv.de/4d52c7dd3e7abf1a4fef932815b5bcfbf0c8287810f8940f5a5dd44325701648?color=5a5a5a) . Also auch der Funktion von
. Also auch der Funktion von  , jedoch um
, jedoch um  auf der
auf der  -Achse verschoben.
-Achse verschoben.
Ein Term für Phase 3 lautet folglich .
.
Ein Term für Phase 3 lautet folglich
(2)
Der Übergang zu einer konstanten Funktion ist knickfrei, wenn diese parallel zur  -Achse ist, also die Steigung Null.
-Achse ist, also die Steigung Null.
 Die Tangente ist nur näherungsweise parallel und der Übergang somit nicht knickfrei.
Die Tangente ist nur näherungsweise parallel und der Übergang somit nicht knickfrei.
(3)
Die Länge der Strecken kann über ein Flächenntegral ermittelt werden.
Die Grenzen entsprechen demjenigen Intervall, in welchem die Phase ist. Integriert werden muss nur, wenn der Graph im Intervall eine Fläche einschließt. Phase 1 läuft im Intervall ![\([0; 4,2]\)](https://mathjax.schullv.de/0a154bcc636a5384e37f1f0d8a12e9abba4fe9f262bb4ee79bf4e2dd4311347c?color=5a5a5a) und Phase 3 im Intervall
und Phase 3 im Intervall ![\([9,2; 15]\)](https://mathjax.schullv.de/e124455048fa2a0c60960cddea8a2c3703598d88dc99e680156ee5fef3434289?color=5a5a5a) .
Die gesuchte Länge entspricht also:
Der Tiger erreicht eine Durchschnittsgeschwindigkeit von ca.
.
Die gesuchte Länge entspricht also:
Der Tiger erreicht eine Durchschnittsgeschwindigkeit von ca. 
e)
Bisher wird die Höchstgeschwindigkeit von ca.  nach ca.
nach ca.  erreicht.
Die benötigten Dehnungen in
erreicht.
Die benötigten Dehnungen in  - bzw. in
- bzw. in  -Richtung werden von
-Richtung werden von  geliefert. Es folgt
geliefert. Es folgt  und
und 