Vektorielle Geometrie
Eine ehemalige Lagerhalle soll für ein Theater umgebaut werden. Die Lagerhalle hat eine quadratische Grundfläche mit einer Seitenlänge von 
Die Grundfläche liegt in der 
-Ebene.
Die Höhe der Halle beträgt 
Als „Himmel“ wird, wie in der Abbildung modellhaft dargestellt ist, eine dreieckige Plane aufgespannt.
Gegeben sind die Punkte 
und 
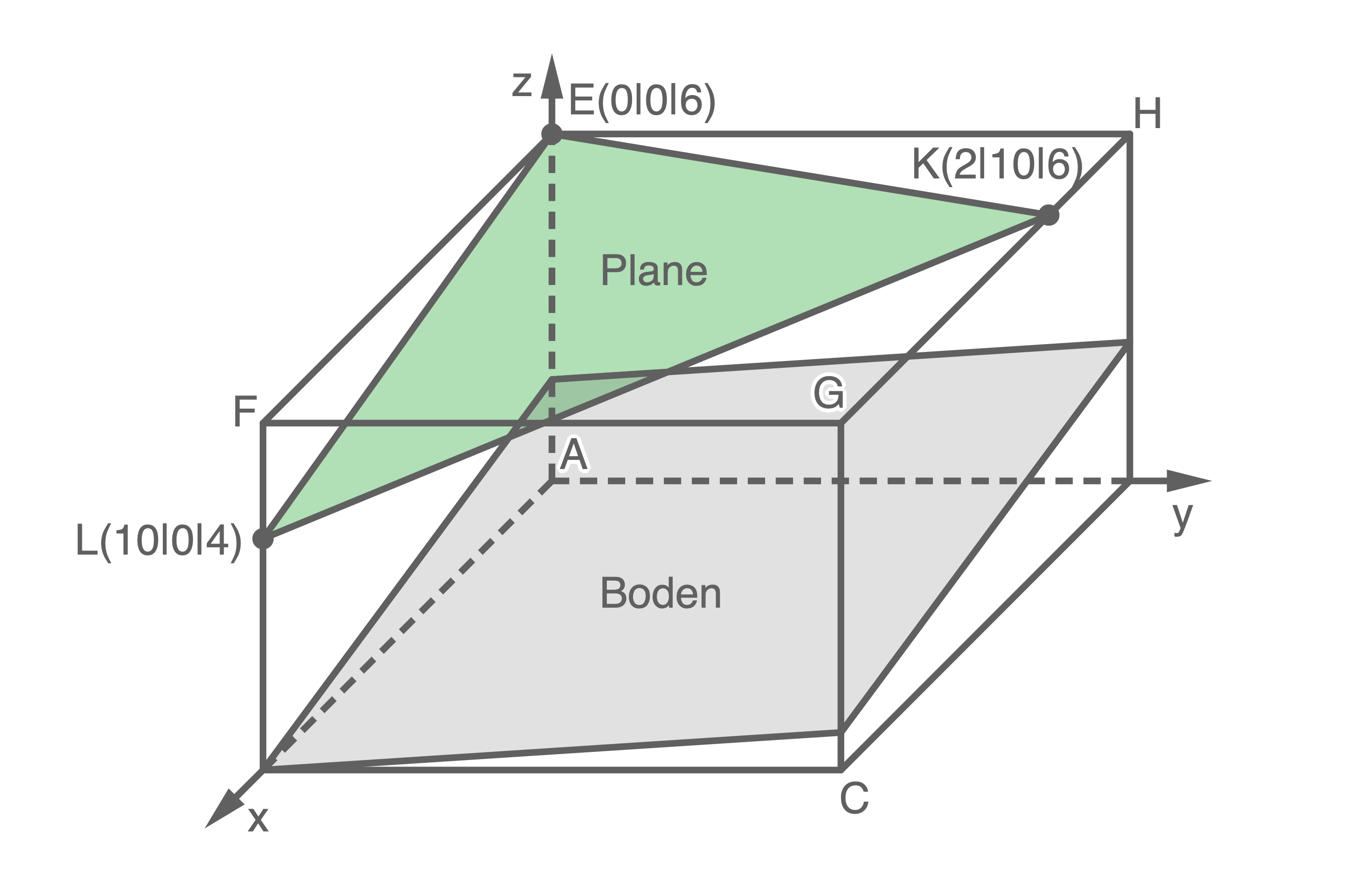
a)
Gib die Koordinaten der Punkte 
und 
an. Untersuche, ob die Plane die Form eines gleichschenkligen Dreiecks hat.
(2 Punkte)
b)
Die Plane liegt in einer Ebene 
Bestimme eine Gleichung der Ebene 
in Parameter- und in Koordinatenform.
(3 Punkte)
c)
In die Lagerhalle wird ein Boden für den Zuschauerraum eingebaut. Der Boden soll in der Ebene 
liegen, die parallel zur Plane und durch den Punkt 
verläuft.
Begründe, dass die Ebene durch die Gleichung 
beschrieben werden kann. Ermittle, wie groß die maximale Höhe des Bodens über der Grundfläche ist.
Begründe, dass die Ebene
(6 Punkte)
d)
Begründe, dass der Abstand der Plane vom Boden des Zuschauerraums kleiner als 
ist.
(3 Punkte)
e)
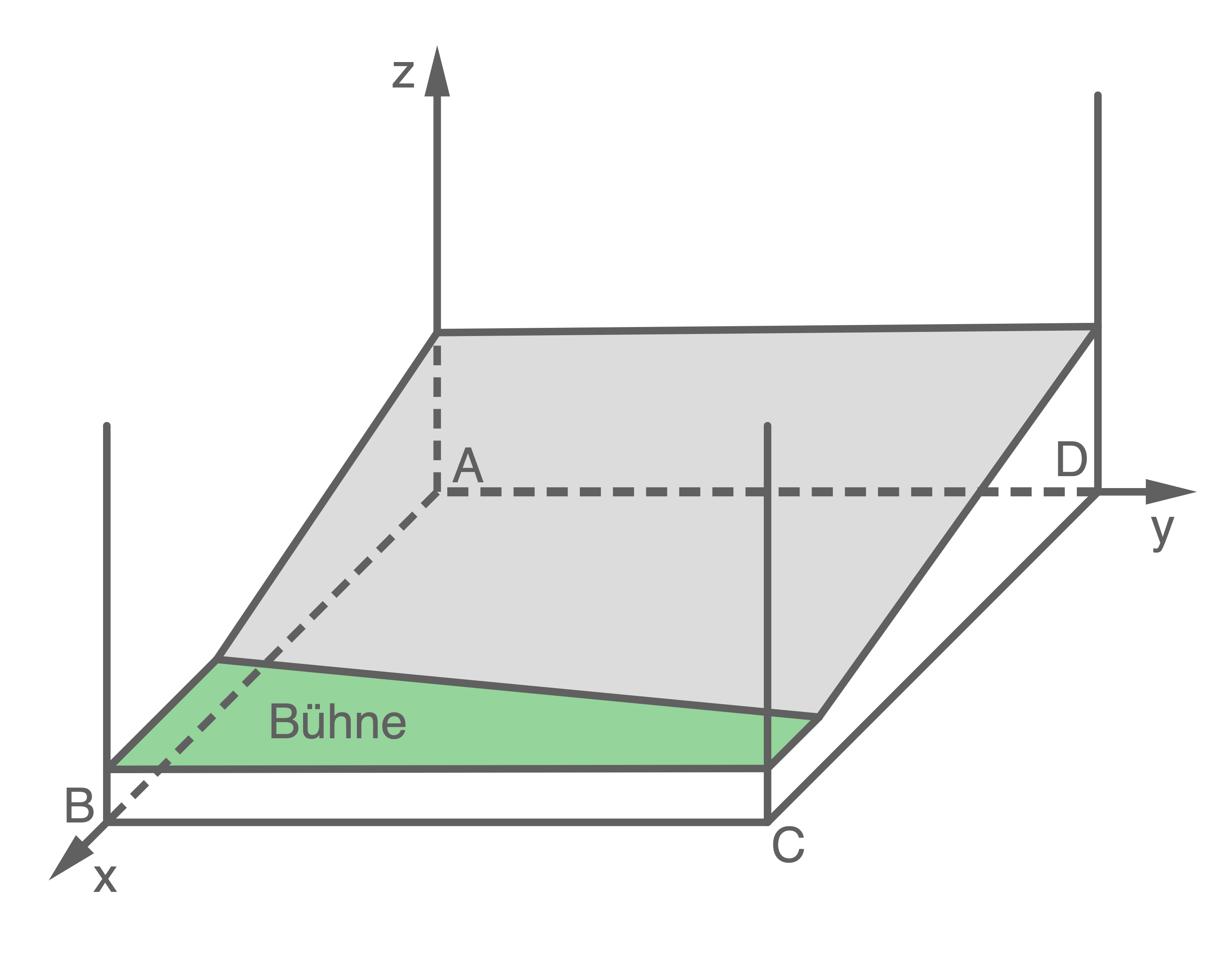
Für die Schauspieler wird schließlich eine Bühne eingebaut. Der Boden der Bühne verläuft parallel zur Grundfläche der Halle in einer Höhe von 
soweit, bis sie auf den Boden des Zuschauerraums trifft.
Berechne die Größe der trapezförmigen Bühnenfläche.
(6 Punkte)
(20 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Koordinaten der Punkte und angeben
Mit der Höhe der Halle von 
und einer Grundfläche von 
folgen die Koordinaten der Punkte mit:
und 
Form der Plane untersuchen
Ein Dreieck ist gleichschenklig, wenn es zwei Seiten hat, die gleich lang sind.
Längen der Seiten berechnen:
![\(\vert \overrightarrow{EK} \vert = \left\vert \pmatrix{2\\10\\0}\right\vert = \sqrt{104} \approx 10,2 \;[\text{m}]\)](https://mathjax.schullv.de/e03dea43231265816c11bb20f8872026dc18bd6ca0b92b1f12701fce17d5a9b9?color=5a5a5a)
![\(\vert \overrightarrow{EL} \vert = \left\vert \pmatrix{0\\10\\-2}\right\vert = \sqrt{104} \approx 10,2 \;[\text{m}]\)](https://mathjax.schullv.de/86891b5a7f679afd15ed6a9d8eaf4b26528b8212eb54aa8b973bdbd39dad0926?color=5a5a5a)
Somit ist die Bedingung erfüllt und die Plane hat die Form eines gleichschenkligen Dreiecks.
b)
Parameterform von 
aufstellen
Eine Parameterform der Ebene kann beispielsweise wie folgt aufgestellt werden:
Koordinatenform von bestimmen
Aus den beiden Richtungsvektoren der Parameterform kann durch das Kreuzprodukt ein Normalenvektor der Ebene aufgestellt werden:
Einsetzen von 
und 
in die allgemeine Koordinatengleichung ergibt:
![\(\begin{array}[t]{rll}
-20 \cdot x +4y -100\cdot c &=& a& \\[5pt]
-20 \cdot 10 -100 \cdot 4&=& a&\\[5pt]
-600&=& a
\end{array}\)](https://mathjax.schullv.de/76567e6821b8bc0996614907442b6b4553c5a600a72540d2a57249a9834e2b09?color=5a5a5a)
Die Koordinatenform ergibt sich nun mit:
![\(\begin{array}[t]{rll}
-20 x +4 y-100 z&=&-600 &\quad \scriptsize \mid\; :(-4)\\[5pt]
5 x - y+25 z&=&150
\end{array}\)](https://mathjax.schullv.de/a7133734ed61269322b8843c82fd2ca882b51c1129d4cb77c6a05627725b0d1b?color=5a5a5a)
c)
Beschreibung durch 
begründen
Sind Ebenen parallel, so stimmen ihre Normalenvektoren überein, deshalb lässt sich mit der Koordinatengleichung 
darstellen.
Durch Einsetzen von 
in die Gleichung kann 
berechnet werden:
![\(\begin{array}[t]{rll}
5\cdot10-1\cdot0+25\cdot0&=& d \\[5pt]
50&=&d
\end{array}\)](https://mathjax.schullv.de/ae49aa69dc352d10ea5ab94c43ab73d1d2b01e328e1cf9b706275a65a484bf0d?color=5a5a5a)
Die Ebene kann also durch 
beschrieben werden.
Maximale Höhe berechnen
Die maximale Höhe des Bodens wird an dem Eckpunkt des Bodens angenommen, der auf der Kante 
liegt. Für diesen gilt 
und 
.
Einsetzen der Koordinaten in die Ebenengleichung ergibt:
![\(\begin{array}[t]{rll}
5\cdot0-1\cdot10+25z&=&50 &\quad \scriptsize \mid\;+10\;\mid\;:25 \\[5pt]
z&=&2,4
\end{array}\)](https://mathjax.schullv.de/09f93a7a184a9a8d1d802babfb29105d3ba66eb3bd5f664df6e3a72f4e9c613a?color=5a5a5a)
Die maximale Höhe des Bodens über der Grundfläche beträgt somit 
d)
Da die Plane parallel zum Boden des Zuschauerraums verläuft, kann anhand von zwei übereinanderliegenden Punkten der vertikale Abstand bestimmt werden:
Der Punkt 
der Plane und Punkt des Bodens liegen beispielsweise übereinander, sodass anhand der Differenz der 
-Koordinaten ein Abstand von genau 
Metern ermittelt werden kann.
Da 
jedoch nicht senkrecht zu den Ebenen liegt, ist der tatsächliche Abstand der beiden Ebenen kleiner als Meter.
e)
1. Schritt: Gleichung der Schnittgeraden bestimmen
Die Schnittgerade 
von und der Bühnenebene kann durch Einsetzen der Höhe 
in die Ebenengleichung des Bodens ermittelt werden:
![\(\begin{array}[t]{rll}
5x -y+25z &=& 50 &\quad \scriptsize \mid\; z=0,8 \\[5pt]
5x -y +25\cdot 0,8&=& 50
\end{array}\)](https://mathjax.schullv.de/6604974490f0027240e267199ab903799b6f9d292054ac5bb74647a4639c0904?color=5a5a5a)
Für 
folgt 
.
Somit lautet die Gleichung der Schnittgeraden:
2. Schritt: Größe der Bühnenfläche berechnen
Ermitteln der 
-Koordinaten der Schnittpunkte von mit den Seitenflächen 
und 
des Theaters:
Für den Schnittpunkt 
gilt :
![\(\begin{array}[t]{rll}
y&=& 0& \\[5pt]
-30+5r&=& 0&\quad \scriptsize \mid\; +30 \quad \scriptsize \mid\; :5 \\[5pt]
r&=& 6 &\\[5pt]
x&=& 6
\end{array}\)](https://mathjax.schullv.de/d7d14f2ac77413887dc565d905359b5d73239e55a155b59a0c24fd42120d8400?color=5a5a5a)
Für den Schnittpunkt 
gilt :
![\(\begin{array}[t]{rll}
y&=& 10& \\[5pt]
-30 +5r&=& 10 &\quad \scriptsize \mid\;+30 \quad \scriptsize \mid\; :5 \\[5pt]
r&=& 8& \\[5pt]
x&=&8
\end{array}\)](https://mathjax.schullv.de/d2e92b23540568df317bc02b281a2928b5bdca5c995497fcfd463409eb3fa6e5?color=5a5a5a)
Somit haben die parallelen Trapezseiten Längen von 
bzw. 
Mit der Formel für den Flächeninhalt eines Trapezes folgt:
Die Bühne hat also eine Fläche von 