Vektorielle Geometrie

Ein neu geplantes Mehrfamilienhaus soll $9\,\text{m}$ breit, $15\,\text{m}$ lang und inklusive Dach $9\,\text{m}$ hoch werden.

Der Erdboden wird durch die $xy$ -Ebene beschrieben. In dieser Ebene liegen die Eckpunkte $A,$ $B,$ $C$ und $D$ des rechteckigen Hausbodens. Der Punkt $G$ hat die Koordinaten $G(9\mid 15\mid 6).$ Der Dachfirst $\overline{IJ}$ verläuft horizontal und mittig über der Dachbodenfläche $EFGH.$

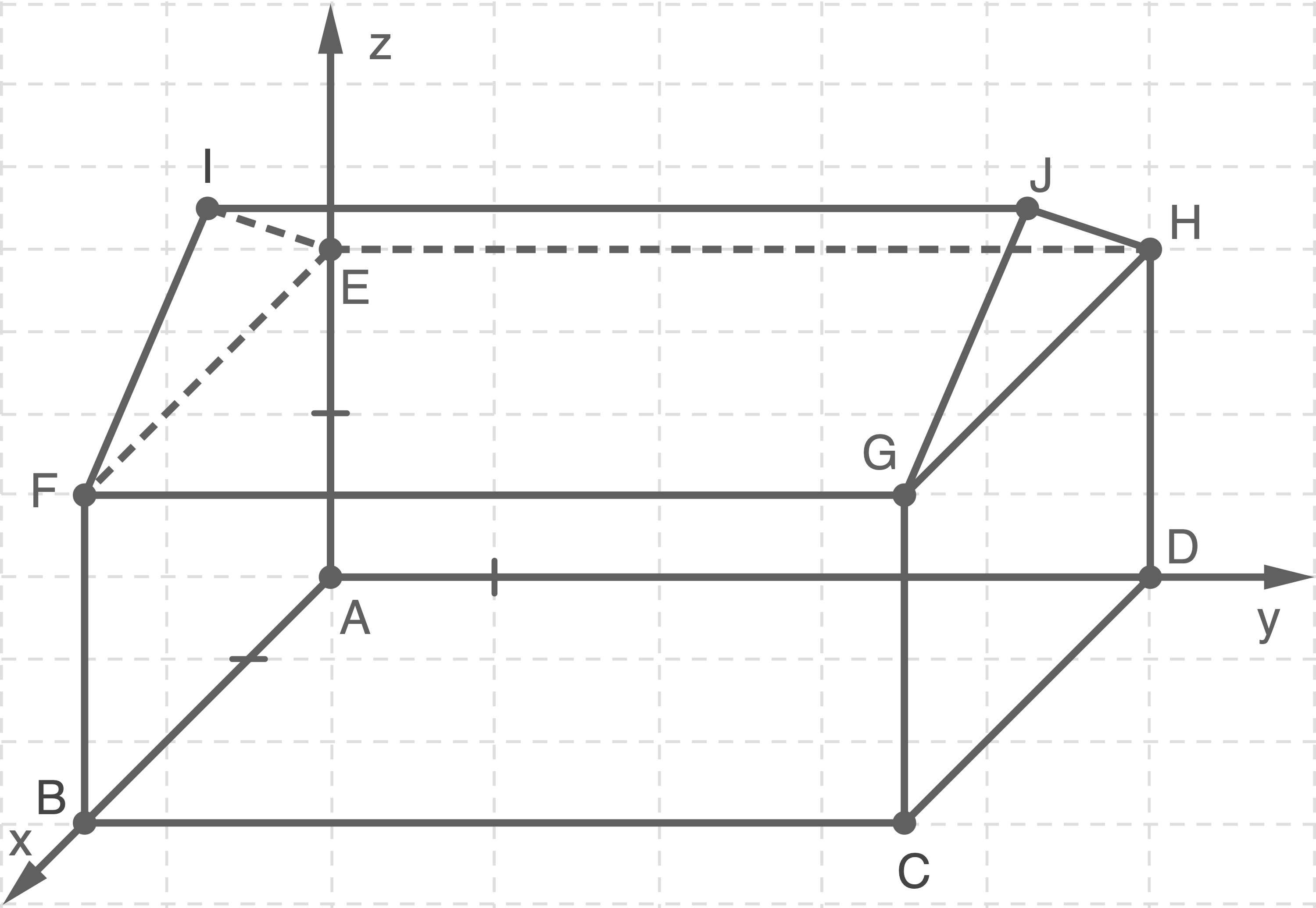
Diagramm eines dreidimensionalen Koordinatensystems mit Punkten und Linien.

Gib die Koordinaten der Punkte $C,$ $F$ und $J$ an.

Beschrifte die Achsen im Material mit einer geeigneten Skalierung.

(2 Punkte)

Gib eine Parametergleichung der Ebene $T$ an, in der die Dachfläche $FGJI$ liegt.

[Zur Kontrolle: $2x+3z = 36$ ist eine mögliche Koordinatengleichung der Ebene.]

(2 Punkte)

Berechne den Flächeninhalt der gesamten Dachfläche des Hauses.

(2 Punkte)

Berechne das Volumen des Mehrfamilienhauses.

(2 Punkte)

Damit das Dach für die geplante Installation einer Photovoltaikanlage geeignet ist, sollte die Dachneigung zwischen 30 und 35 Grad betragen. In diesem Sachzusammenhang wird folgende Rechnung durchgeführt:

(1)

$\overrightarrow{u}_1 = \pmatrix{-4,5\\0\\3},$ $\overrightarrow{u}_2 = \pmatrix{-9\\0\\0}$

(2)

$\cos \alpha = \frac{\pmatrix{-4,5\\0\\3}\cdot \pmatrix{-9\\0\\0}}{\left| \pmatrix{-4,5\\0\\3}\right| \cdot \left| \pmatrix{-9\\0\\0}\right|} = ...$

Erläutere den Ansatz in Zeile (1) und den Rechenschritt in Zeile (2).

Berechne den Winkel $\alpha.$

Deute dein Ergebnis für $\alpha$ im Sachzusammenhang.

(4 Punkte)

Auf dem Nachbargrundstück steht eine $13,5\,\text{m}$ hohe Tanne im Punkt $P(30,75\mid 6\mid 0).$

Zu einem bestimmten Zeitpunkt fällt das Sonnenlicht in Richtung des Vektors $\overrightarrow{v} = \pmatrix{-2\\0\\-0,5}$ auf die Dachfläche $FGJI.$

Prüfe, ob der Schatten der Tannenspitze zu diesem Zeitpunkt auf die Dachfläche $FGJI$ trifft.

(4 Punkte)

Im Garten des Hauses soll ein Blumenbeet angelegt werden. Dafür sollen Pflanzen dreier Pflanzengattungen gekauft werden. Eine Pflanze der Gattung Sonnenhut kostet $3\,€,$ eine der Gattung Phlox $4\,€$ und eine der Gattung Malve $6\,€.$ Es sollen genau $25$ Pflanzen für insgesamt $100\,€$ gekauft werden. Darunter sollen doppelt so viele Pflanzen der Gattung Sonnenhut wie Pflanzen der Gattung Malve sein.

Mithilfe der Informationen im Text wird das folgende lineare Gleichungssystem aufgestellt:

$\begin{array}{llllll} \text{I}\quad&x_s & &-2x_M &=& 0 \\ \text{II}\quad& x_s& +x_p& +x_M &=& 25 \\ \text{III}\quad&3x_s&+4x_p& +6x_M &=& 100 \\ \end{array}$

Gib eine Definition der verwendeten Variablen an.
Erläutere die Bedeutung der einzelnen Gleichungen im Sachzusammenhang.

(2 Punkte)

Das lineare Gleichungssystem besitzt ohne Beachtung des Sachzusammenhangs unendlich viele Lösungen.

Berechne diese Lösungen.

(2 Punkte)

(20 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

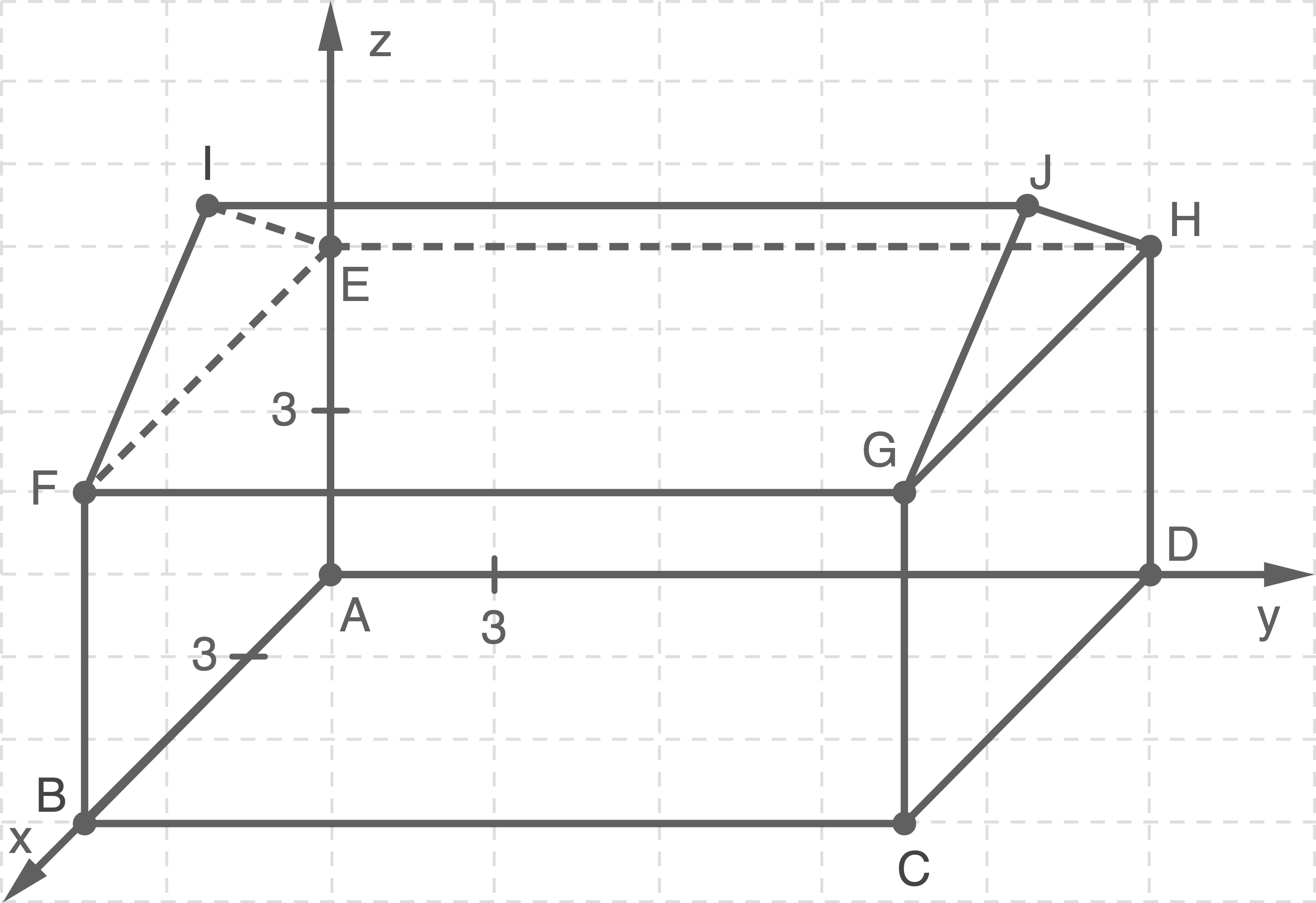
Koordinaten angeben

Durch Ablesen an den Achsen folgt:

$C(9\mid 15\mid 0)$

$F(9\mid 0\mid 6)$

$J(4,5\mid 15\mid 9)$

Achsen beschriften

Eine Parametergleichung der Ebene $FGJI$ kann beispielsweise wie folgt bestimmt werden:

$T:\overrightarrow{x}=\overrightarrow{OG} + r\cdot \overrightarrow{GF} + s\cdot \overrightarrow{GJ}$

Parametergleichung anzeigen

Da beide Dachflächen identisch und rechteckig sind, kann der gesuchte Flächeninhalt wie folgt berechnet werden:

Rechenweg anzeigen

$A \approx 162,25 \,\left[\text{m}^2\right]$

Die gesamte Dachfläche ist somit ca. $162,25 \,\text{m}^2$ groß.

1. Schritt: Volumen des Dachs berechnen

Das Dach hat die Form eines Prismas mit dreiseitiger Grundfläche. Die Höhe des Prismas entspricht der Länge des Hauses und somit $15\,\text{m}$ Die dreieckige Grundfläche ist ein gleichseitiges Dreieck, beispielsweise die Fläche $GHJ.$ Sie besitzt die Grundseite $\overline{GH}$ mit einer Länge von $9\,\text{m},$ die Breite des Hauses, und eine Höhe von $3\,\text{m},$ die Höhe des Dachbodens.

$\begin{array}[t]{rll} V_{\text{Dach}}&=& \dfrac{1}{2}\cdot 9 \,\text{m} \cdot 3\,\text{m} \cdot 15\,\text{m} \\[5pt] &=& 202,5\,\text{m}^3 \end{array}$

2. Schritt: Volumen des Hauses berechnen

Der untere Teil des Hauses hat die Form eines Quaders mit einer Länge von $15\,\text{m},$ einer Breite von $9\,\text{m}$ und einer Höhe von $6\,\text{m}.$

$\begin{array}[t]{rll} V_{\text{Quader}}&=& 15\,\text{m}\cdot 9\,\text{m} \cdot 6\,\text{m} \\[5pt] &=& 810\,\text{m}^3 \end{array}$

Das gesamte Volumen des Hauses beträgt daher:

$\begin{array}[t]{rll} V &=& V_{\text{Dach}} + V_{\text{Quader}} \\[5pt] &=& 202,5\,\text{m}^3 + 810\,\text{m}^3 \\[5pt] &=& 1.012,5\,\text{m}^3 \end{array}$

Das Gesamtvolumen des Hauses beträgt somit $1.012,5\,\text{m}^3.$

Ansatz (1) erläutern

Der Vektor $\overrightarrow{u_1} = \pmatrix{-4,5\\0\\3}$ entspricht dem Verbindungsvektor $\overrightarrow{GJ}$ und der Vektor $\overrightarrow{u_2} = \pmatrix{-9\\0\\0}$ entspricht dem Verbindungsvektor $\overrightarrow{GH}.$

Da sowohl die Dachbodenfläche als auch die Dachfläche $FGJI$ rechteckig sind und beide die gemeinsame Kante $\overline{FG}$ besitzen, entspricht der Winkel, den diese beiden Flächen einschließen, dem Winkel, den die beiden Seitenkanten $\overline{GJ}$ und $\overline{GH}$ einschließen.

Rechenschritt (2) deuten

In Schritt (2) wird dann nun Winkel zwischen den beiden Vektoren $\overrightarrow{GJ}$ und $\overrightarrow{GH}$ und somit der Winkel zwischen den beiden Kanten mithilfe der entsprechenden Formel zur Bestimmung eines Winkels zwischen zwei Vektoren bestimmt.

Winkel berechnen

Rechenweg anzeigen

$\alpha \approx 33,7^{\circ}$

Der Winkel $\alpha$ beträgt folglich etwa $33,7^{\circ}.$

Ergebnis deuten

Die Dachneigung beträgt ca. $33,7^{\circ}.$ Damit ist das Dach in Bezug auf die Dachneigung für die Installation einer Photovoltaikanlage geeignet.

Da die Tanne im Punkt $P(30,75\mid 6\mid 0)$ steht, befindet sich ihre Spitze im Punkt $S(30,75\mid 6\mid 13,5).$ Die Tannenspitze und ihr Schattenpunkt liegen daher auf der Geraden $g$ entlang der Sonnenstrahlen mit folgender Gleichung:

$\begin{array}[t]{rll} g:\, \overrightarrow{x} &=& \overrightarrow{OS} + t\cdot \overrightarrow{v}\\[5pt] &=& \pmatrix{30,75\\ 6\\13,5 } + t\cdot \pmatrix{-2\\0\\-0,5} \end{array}$

1. Schritt: Schnittpunkt von $T$ und $g$ bestimmen

Durch die Verwendung der Parametergleichung von $T$ kann später anhand der berechneten Parameterwerte argumentiert werden, ob der Schnittpunkt innerhalb oder außerhalb des Rechtecks liegt.

Rechnung anzeigen

Es ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&21,75 &=& 0r -4,5s +2t \\ \text{II}\quad&-9 &=& -15r +0s +0t \\ \text{III}\quad&7,5&=& 0r +3s +0,5t \\ \end{array}$

Mit dem CAS lässt sich das Gleichungssystem wie folgt lösen:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 3: Algebra $\to$ 7

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math1 $\to$ $\{^{\Box}_{\Box}$

Der Schattenpunkt der Tannenspitze lässt sich mithilfe der Parameterwerte $r= 0,6$ und $s=0,5$ als Punkt der Ebene $T$ darstellen.

2. Schritt: Lage des Punkts überprüfen

Das Rechteck $FGJI$ wird durch die beiden Vektoren $\overrightarrow{GF}$ und $\overrightarrow{GJ}$ aufgespannt. Alle Punkte innerhalb dieses Rechtecks lassen sich daher durch die Gleichung $\overrightarrow{OG} + r\cdot \overrightarrow{GF} + s\cdot \overrightarrow{GJ}$ mit $0\leq r\leq 1$ und $0\leq s\leq 1$ beschreiben.

Im ersten Schritt wurde berechnet, dass sich der Schattenpunkt $\(S$ der Tannenspitze als $\overrightarrow{OS‘} = \overrightarrow{OG} + r\cdot \overrightarrow{GF} + s\cdot \overrightarrow{GJ}$ mit $r=0,6$ und $s=0,5$ beschreiben lässt. Er liegt also innerhalb des Rechtecks $FGJI.$

Der Schatten der Tannenspitze trifft zum betrachteten Zeitpunkt somit auf die Dachfläche $FGJI.$

Definition angeben

$x_s:$

Anzahl der Pflanzen der Gattung Sonnenhut

$x_p:$

Anzahl der Pflanzen der Gattung Phlox

$x_M:$

Anzahl der Pflanzen der Gattung Malve

Bedeutung erläutern

$\text{I}$

Die Anzahl der Pflanzen der Gattung Sonnenhut ist doppelt so groß wie die Anzahl der Pflanzen der Gattung Malve.

$\text{II}$

Die Gesamtanzahl der Pflanzen beträgt $25.$

$\text{III}$

Die Gesamtkosten der Pflanzen betragen $100\,€.$

Für $x_s = t$ lässt sich das Gleichungssystem wie folgt lösen:

$\begin{array}{llllll} \text{I}:\quad&t & & -2x_ M &=& 0 \\ \text{II}:\quad& t& +x_p& +x_M &=& 25 \\ \text{III}:\quad&3t&+4x_p& +6x_M &=& 100 \\ \end{array}$

Aus Zeile $\text{I}$ folgt:

$\begin{array}[t]{rll} \text{I}:& t -2x_M&=& 0&\quad \scriptsize \mid\; -t \\[5pt] & -2x_M &=& -t &\quad \scriptsize \mid\; :(-2) \\[5pt] & x_M &=& 0,5t \\[5pt] \end{array}$

Einsetzen in $\text{II}$ liefert:

Rechenweg anzeigen