Aufgabe 3

In Abbildung 1 ist ein regelmäßiges Tetraeder $ABCD$ mit den Eckpunkten $A(0\mid 0\mid 0)$ , $B(10\mid 10\mid0)$ , $C(10\mid 0\mid 10)$ und $D(0\mid 10\mid 10)$ in einem kartesischen Koordinatensystem abgebildet.

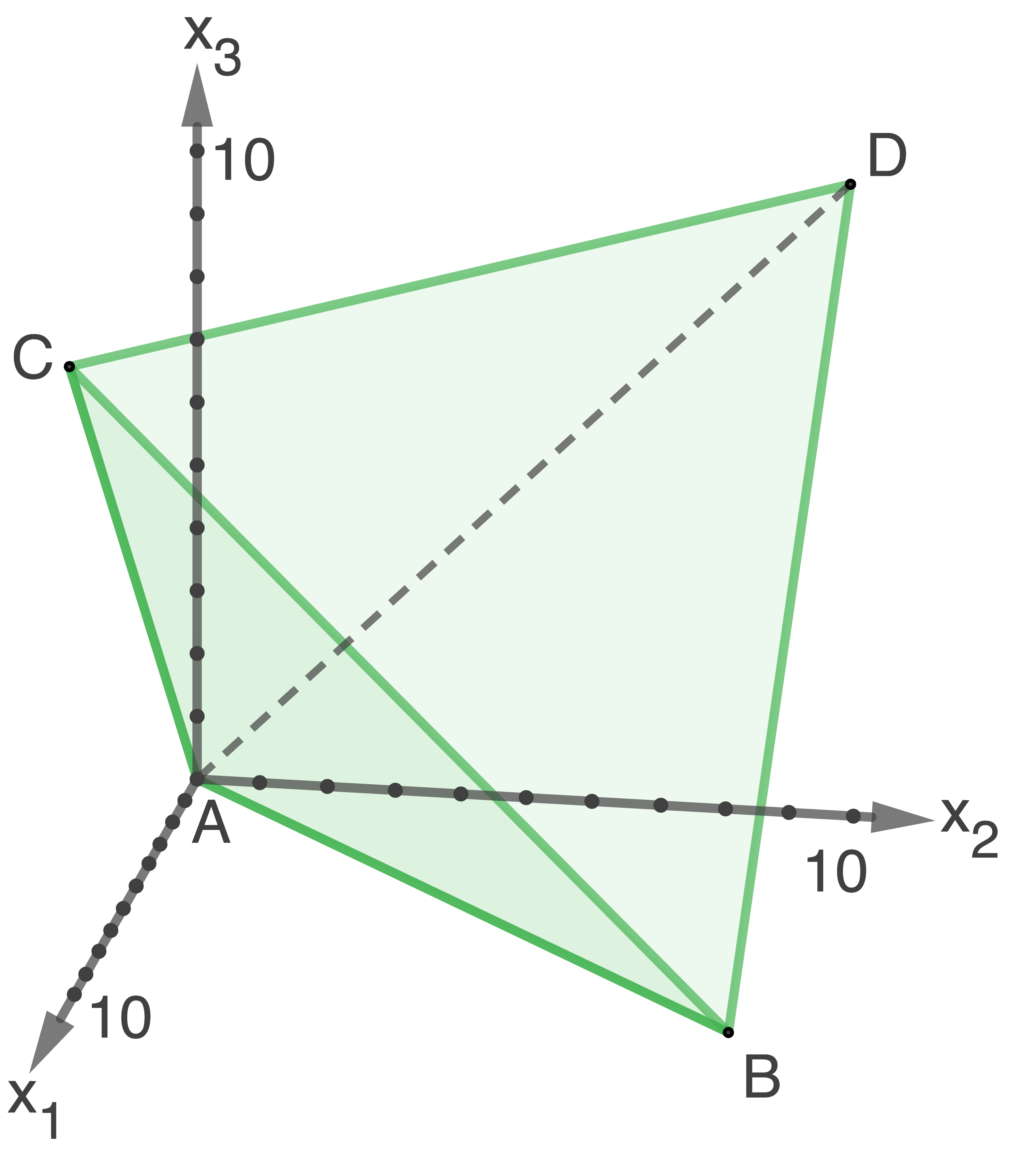
Grafik eines dreidimensionalen Koordinatensystems mit Punkten A, B, C und D sowie einem grünen Bereich.

Abbildung 1

(1)

Gib die Koordinaten des Mittelpunktes $M$ von $\overline{AB}$ an.

(2)

Zeige, dass das Dreieck $ABC$ gleichseitig ist.

(3)

Bestimme den Flächeninhalt des Dreiecks $ABC$ und den Oberflächeninhalt des Tetraeders $ABCD$ .

[Zur Kontrolle: $O_\text{Tetraeder}= 200 \cdot \sqrt{3}\,\text{FE}$ ]

(4)

Gib die Koordinaten der Eckpunkte eines Würfels mit dem Volumen $V=1000\,\text{VE}$ an, der das Tetraeder enthält.

(2 + 4 + 4 + 4 Punkte)

(1)

$E$ ist die Ebene, in der das Dreieck $ABC$ liegt, und

$g:\overrightarrow{x}= \pmatrix{0\\10\\10}+t \cdot \pmatrix{1\\-1\\-1},\,$ $t\in \mathbb{R},$

ist eine Gerade, die durch den Punkt $D$ verläuft.
Bestimme rechnerisch den Schnittpunkt $P$ von $g$ und $E.$

[ Zur Kontrolle: $P\left(\frac{20}{3}\mid\frac{10}{3}\mid\frac{10}{3}\right)$ ]

(2)

Zeige, dass $\overrightarrow {DP}$ auf $\overrightarrow {AB}$ und $\overrightarrow {AC}$ senkrecht steht.

(3)

Bestimme rechnerisch das Volumen des Tetraeders $ABCD$ .

(6 + 3 + 3 Punkte)

Das Tetraeder $ABCD$ modelliert einen Körper mit Kanten aus Draht. Diesen Körper taucht man in Seifenlauge. Beim Herausnehmen bilden sich im Inneren des Körpers Flächen aus Seifenhaut (vgl. Abbildungen 2 und 3).

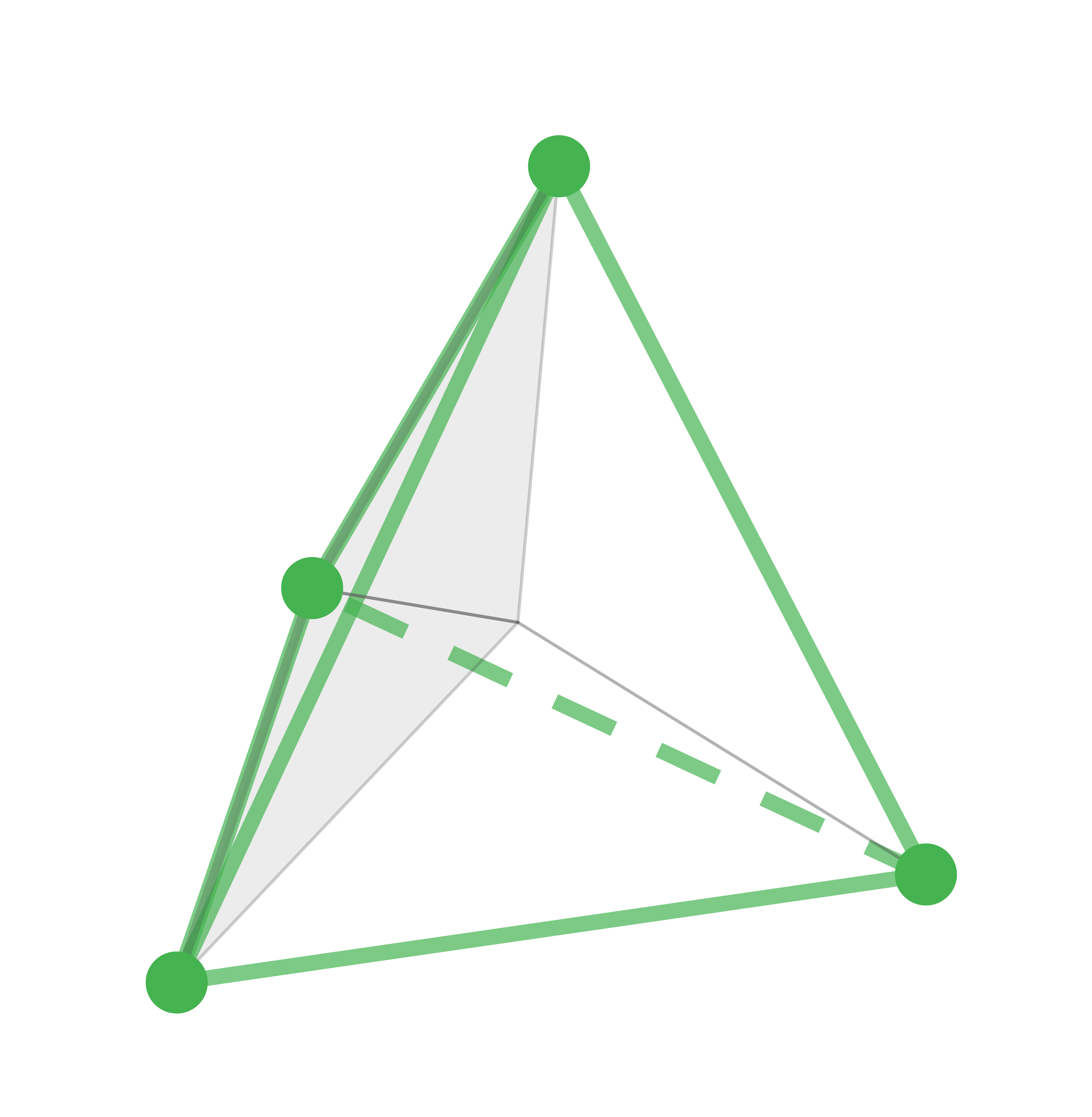
3D-Darstellung eines Tetraeders mit grünen Punkten und Linien in verschiedenen Schattierungen.

Abbildung 2

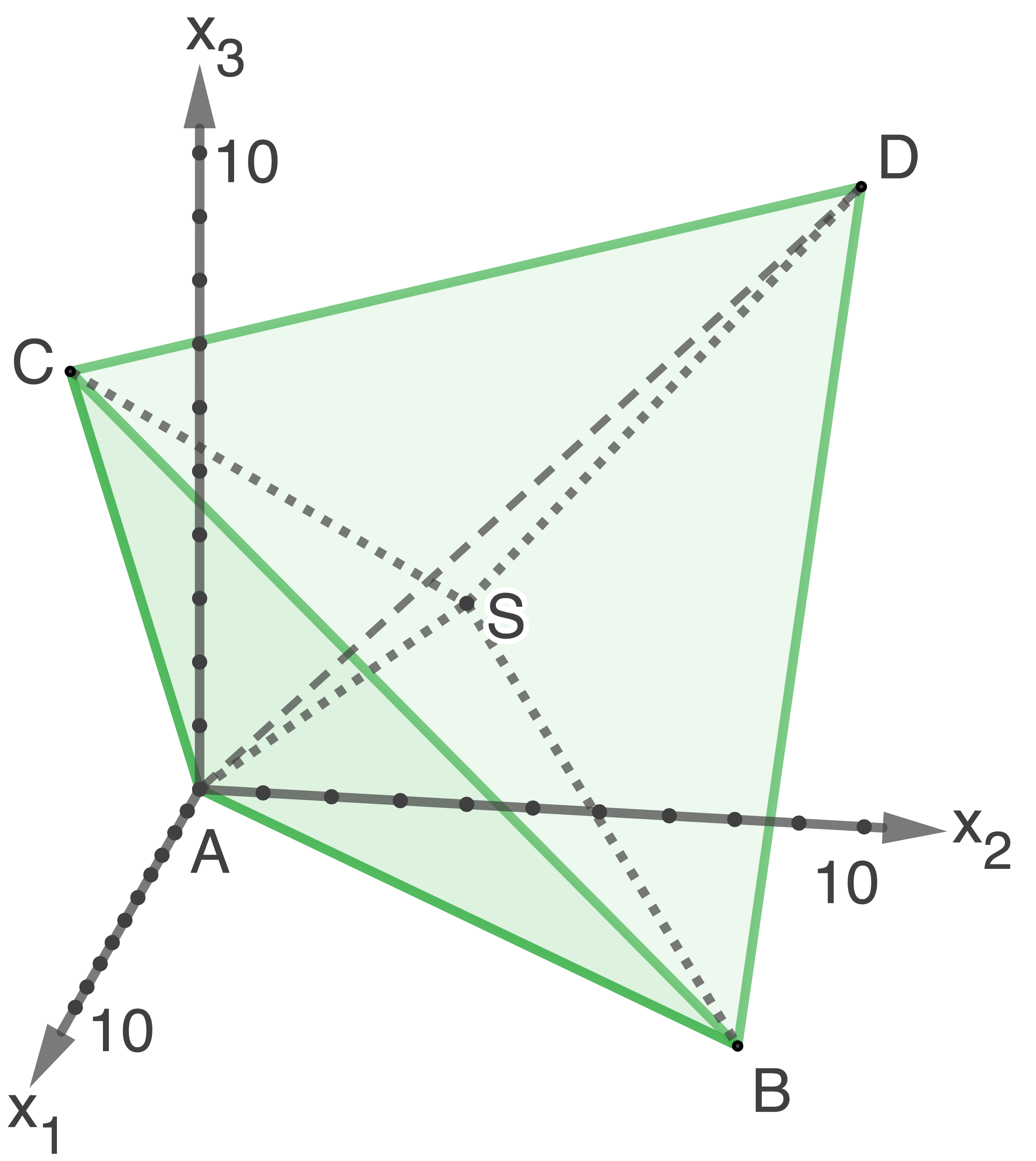
3D-Diagramm mit Punkten A, B, C, D und Fläche S in einem Koordinatensystem.

Abbildung 3

Die Seifenhaut besteht aus sechs kongruenten gleichschenkligen Dreiecken mit einem gemeinsamen Eckpunkt, der durch $S(5\mid 5\mid 5)$ modelliert wird. $S$ liegt im Inneren des Tetraeders. Jedes dieser Dreiecke hat den Flächeninhalt $F=25\cdot\sqrt{2}\,\text{FE}$ .

(1)

Bestimme, um wie viel Prozent der Gesamtflächeninhalt der Seifenhaut kleiner ist als der Oberflächeninhalt des Tetraeders.

(2)

Berechne die Größe des Winkels zwischen $\overrightarrow{SB}=\left(\begin{array}{l} 5\\ 5\\ -5 \end{array}\right)$ und $\overrightarrow{SD}=\left(\begin{array}{l} -5\\ 5\\ 5 \end{array}\right).$

(3)

Weise rechnerisch nach, dass der Punkt $S$ auf der Strecke $\overline{DP}$ liegt.

(4)

Begründe, dass das Volumen der Pyramide $ABCS$ ein Viertel des Volumens des Tetraeders $ABCD$ beträgt.

(3 + 3 + 5 + 3 Punkte)

(1)

Die Koordinaten des Mittelpunktes werden wie folgt berechnet:

$\overrightarrow{0M} = \dfrac{1}{2} \cdot \overrightarrow{AB} =\dfrac{1}{2} \cdot \pmatrix {10\\10\\0} = \pmatrix {5\\5\\0}$ .

Die Koordinaten des Mittelpunktes sind : $M(5 \mid 5 \mid 0)$ .

(2)

Das Dreieck ist gleichseitig, wenn alle Seiten gleich lang sind.

$\mid\overrightarrow{AB} \mid = \mid \overrightarrow{AC}\mid =\mid \overrightarrow{BC}\mid$

Vollständige Lösung anzeigen

Damit ist das Dreieck $ABC$ gleichschenklig.

(3)

Der Flächeninhalt eines Dreiecks wird mit $A= \dfrac{1}{2} \cdot a \cdot h_a$ berechnet. Da der Mittelpunkt der Strecke $\overline{AB}$ schon bekannt ist, ist es geschickt, $\overline{AB}$ als $a$ zu wählen.

$A= 50 \cdot \sqrt{3}, \, \, O= 200 \cdot \sqrt{3}$

Vollständige Lösung anzeigen

(4)

Ein Würfel mit 6 Seiten und einem Volumen von $V=1000\;\text{VE}$ hat die Seitenlängen $10\;\text{LE}.$ Deshalb sind die Koordinaten der Punkte:

$P_1(0 \mid 0 \mid 0)$ , $P_2(10\mid 0 \mid 0)$ , $P_3(0\mid 10 \mid 0)$ , $P_4(0 \mid 0 \mid 10)$ , $P_5(10 \mid 10 \mid0)$ , $P_6(10 \mid 0 \mid 10)$ , $P_7(0 \mid 10 \mid 10)$ , $P_8(10 \mid 10 \mid 10)$

(1)

Eine Gleichung der Ebene die durch das Dreieck $ABC$ verläuft, lautet:

$E: x= k\cdot \pmatrix{10\\10\\0} + l \cdot \pmatrix{10\\0\\10}$

Gleichsetzen von $E$ und $g$ zur Ermittlung des Schnittpunktes:

Vollständige Lösung anzeigen

Mit dem TR ergibt sich $t=\dfrac{20}{3}$ , $k=\dfrac{1}{3}$ und $l=\dfrac{1}{3}$ . Einsetzen von $t$ in $g$ ergibt den Punkt $P\left(\dfrac{20}{3} \mid \dfrac{10}{3} \mid \dfrac{10}{3} \right)$ .

(2)

$\overrightarrow{DP} =\pmatrix {\dfrac{20}{3} \\ - \dfrac{20}{3} \\ -\dfrac{20}{3} }$

Mit $\pmatrix {\dfrac{20}{3} \\ - \dfrac{20}{3} \\ -\dfrac{20}{3} }\cdot \pmatrix{10\\10\\0} =0$

und $\pmatrix {\dfrac{20}{3} \\ - \dfrac{20}{3} \\ -\dfrac{20}{3} } \cdot \pmatrix{10\\0\\10}=0$

steht $\overrightarrow{DP}$ senkrecht auf $\overrightarrow{AB}$ und $\overrightarrow{AC}$ .

(3)

Für das Volumen des Tetradeders gilt: $V= \dfrac{1}{3} \cdot A \cdot h_A= \dfrac{1}{3} \cdot A_{ABC} \cdot \mid \overrightarrow{DP} \mid$ .

$V=\dfrac{1000}{3}$

Vollständige Lösung anzeigen

(1)

Der Gesamtflächeninhalt der Seifenhaut beträgt $6 \cdot F = 6\cdot 25 \sqrt{2} = 150 \cdot \sqrt{2}$ .

Der Gesamtflächeninhalt ist $1- \dfrac{150\cdot \sqrt{2}}{200 \cdot \sqrt{2}} \approx 38,76\;\text{%}$ kleiner als der Oberflächeninhalt des Tetraeders.

(2)

Für den Winkel $\alpha$ zwischen $\overrightarrow{SB}$ und $\overrightarrow{SD}$ gilt:

$\cos \alpha = \dfrac{\pmatrix {5\\5\\-5} \cdot \pmatrix {-5\\5\\5}}{ \,\bigg \vert \,\pmatrix {5\\5\\-5} \,\bigg \vert \,\cdot \,\bigg \vert \, \pmatrix {-5\\5\\5} \,\bigg \vert \,} =\dfrac{1}{3}$

$\alpha \approx 109,47\;^{\circ}$

(3)

$\overrightarrow{x}= \pmatrix{0\\10\\10} +r \cdot \pmatrix {\dfrac{20}{3}\\ \dfrac{-20}{3}\\ \dfrac{-20}{3}}$ , $r\in [0;1]$ ist eine Parameterform der Strecke $\overline{DP}.$

$\pmatrix {5\\5\\5}= \pmatrix{0\\10\\10} +r \cdot \pmatrix {\dfrac{20}{3}\\ \dfrac{-20}{3}\\ \dfrac{-20}{3}}$ muss gelöst werden: $r=\dfrac{3}{4}$ .

Mit $r=\dfrac{3}{4}$ liegt $S$ auf $\overline{DP}$ .

(4)

Da der Punkt $S$ die Strecke $\overline{DP}$ im Verhältnis $1:3$ teilt, hat die Höhe der Pyramide $ABCS$ ein Viertel der Länge der Höhe des Tetraeders $ABCD.$ Bei gleicher Grundfläche $ABC$ beträgt das Volumen der Pyramide $ABCS$ ein Viertel des Volumens des Tetraeders $ABCD$ .