Aufgabe 2
Aufgabenstellung
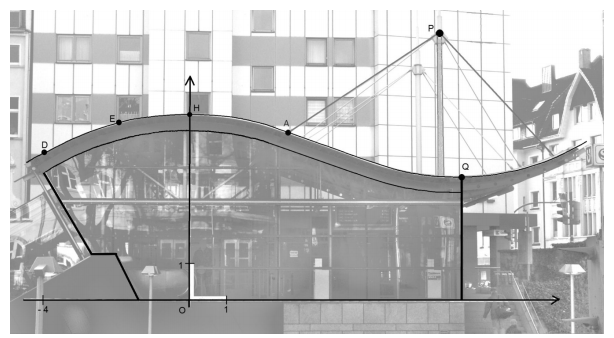
Die Abbildung zeigt das Eingangsgebäude zu einer U-Bahn-Haltestelle. Auf dem Foto schaut man frontal auf eine ebene Glasfläche, die sich unter dem geschwungenen Dach befindet.
Eine Längeneinheit in dem eingezeichneten Koordinatensystem entspricht .
.
Der höchste Punkt der Dachoberkante befindet sich in diesem Koordinatensystem bei und der tiefste Punkt bei
und der tiefste Punkt bei  . Auch die Punkte
. Auch die Punkte  und
und  liegen auf der Dachoberkante.
liegen auf der Dachoberkante.

 Zur Modellierung der Dachoberkante werden für
Zur Modellierung der Dachoberkante werden für  zwei auf
zwei auf  definierte ganzrationale Funktionen vorgeschlagen: Die Funktion
definierte ganzrationale Funktionen vorgeschlagen: Die Funktion  mit
mit  und die Funktion
und die Funktion  mit
mit  .
.






 Bildnachweise [nach oben]
Bildnachweise [nach oben]
Eine Längeneinheit in dem eingezeichneten Koordinatensystem entspricht
Der höchste Punkt der Dachoberkante befindet sich in diesem Koordinatensystem bei
a)
Die Profillinie der Dachoberkante hat eine geschwungene Form, die durch eine ganzrationale Funktion modelliert werden soll.
(1)
Begründe anhand der Abbildung, warum eine ganzrationale Funktion, die zur Modellierung der gesamten Profillinie der Dachoberkante geeignet sein könnte, mindestens  Grades sein muss.
Grades sein muss.
(3P)
(2)
Gib die allgemeine Funktionsgleichung einer ganzrationalen Funktion  Grades an.
Grades an.
Ermittle aus den gegebenen Informationen über die Punkte und
und  vier Bedingungen, mit denen alle Koeffizienten des Funktionsterms berechnet werden können. Gib die Funktionsgleichung an.
vier Bedingungen, mit denen alle Koeffizienten des Funktionsterms berechnet werden können. Gib die Funktionsgleichung an.
Ermittle aus den gegebenen Informationen über die Punkte
(9P)
b)
(1)
Vergleiche die Graphen der beiden Funktionen und erkläre, warum die Funktion  zur Modellierung der Dachoberkante besser geeignet ist.
zur Modellierung der Dachoberkante besser geeignet ist.
(6P)
(2)
Bestimme mit einer hinreichenden Bedingung die Koordinaten des Tiefpunkts  der Funktion
der Funktion  im Modellierungsbereich.
im Modellierungsbereich.
Gib an, um wieviel Prozent jede Koordinate von von der entsprechenden Koordinate von
von der entsprechenden Koordinate von  abweicht.
abweicht.
[Hinweis: Falls du nicht angeben kannst, darfst du im Folgenden ersatzweise mit den Koordinaten von
nicht angeben kannst, darfst du im Folgenden ersatzweise mit den Koordinaten von  weiterarbeiten.]
weiterarbeiten.]
Gib an, um wieviel Prozent jede Koordinate von
[Hinweis: Falls du
(7P)
(3)
Der Punkt  aus der Abbildung hat die
aus der Abbildung hat die  -Koordinate
-Koordinate  .
.
Untersuche im Modell der Funktion , ob an dieser Stelle die Profillinie zwischen
, ob an dieser Stelle die Profillinie zwischen  und
und  das stärkste Gefälle hat.
das stärkste Gefälle hat.
Untersuche im Modell der Funktion
(3P)
c)
Oberhalb des Daches sind geradlinig verlaufende Stahlseile angebracht. Gehe vereinfachend davon aus, dass das Stahlseil von  nach
nach  verläuft.
verläuft.
(1)
Berechne die Länge des Stahlseils von  nach
nach  .
.
(4P)
(2)
Das Stahlseil wird im Bereich  durch eine Gerade
durch eine Gerade  modelliert.
modelliert.
Bestimme eine Gleichung der Geraden und ermittle rechnerisch die Größe der Winkel, die die Gerade
und ermittle rechnerisch die Größe der Winkel, die die Gerade  in
in  mit der Horizontalen und in
mit der Horizontalen und in  mit der Vertikalen einschließt.
mit der Vertikalen einschließt.
Bestimme eine Gleichung der Geraden
(5P)
(3)
Ein weiteres Seil soll von  nach
nach  gespannt werden.
gespannt werden.
Überprüfe, ob es in tangential zur Dachoberkante verlaufen wird.
tangential zur Dachoberkante verlaufen wird.
Überprüfe, ob es in
(4P)
d)
Das Eingangsgebäude ist mit Glas verkleidet. Gehe vereinfachend davon aus, dass es sich bei der in der Abbildung umrahmten Glasfläche um eine durchgehende ebene Fläche handelt, die nicht durch Rahmen und Streben unterbrochen wird.
Die eingezeichnete Oberkante der Glasfläche wird im Bereich durch die auf
durch die auf  definierte Funktion
modelliert.
definierte Funktion
modelliert.
Die eingezeichnete Oberkante der Glasfläche wird im Bereich
(1)
Berechne den Inhalt der Glasfläche von der  -Achse bis zur eingezeichneten Kante durch den Punkt
-Achse bis zur eingezeichneten Kante durch den Punkt  in der Ansicht aus der Abbildung.
in der Ansicht aus der Abbildung.
(4P)
(2)
Für die Glasfläche links von der  -Achse ist der Rand der zu berechnenden Glasfläche in der Abbildung nachgezeichnet.
-Achse ist der Rand der zu berechnenden Glasfläche in der Abbildung nachgezeichnet.
Beschreibe eine mögliche Lösungsidee zur Bestimmung des Inhalts der umrahmten Glasfläche links von der -Achse. Gib dabei alle nötigen Ansätze an, die Berechnung konkreter Werte wird hingegen nicht erwartet.
-Achse. Gib dabei alle nötigen Ansätze an, die Berechnung konkreter Werte wird hingegen nicht erwartet.
Beschreibe eine mögliche Lösungsidee zur Bestimmung des Inhalts der umrahmten Glasfläche links von der
(5P)
© 2016 - Ministerium für Schule und Weiterbildung des Landes Nordrhein-Westfalen.
a)
(1)
(2)
Den Befehl für ein Gleichungssystem findest du wie folgt:
menu  3
3  7
7  1
1
Dann erhältst du folgendes Ergebnis:
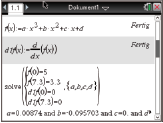 Abb. 1: Funktionsgleichung bestimmen
Abb. 1: Funktionsgleichung bestimmen
b)
(1)
Betrachte beide Graphen und notiere zunächst alle Unterschiede oder auffälligen Gemeinsamkeiten der beiden Graphen. Anschließend kannst du entscheiden, welcher Verlauf besser zu dem der Dachoberkante passt.
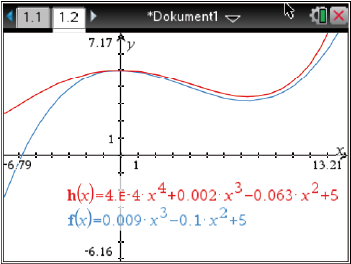 Abb. 2: Vergleich der Graphen
Abb. 2: Vergleich der Graphen
- Beide Graphen besitzen den Hochpunkt
.
- Für
haben beide einen ähnlichen Verlauf, wobei der Graph von
etwas oberhalb des Graphen von
liegt.
- Nur im Bereich
unterscheidet sich der Verlauf etwas deutlicher: Für kleiner werdende
-Werte fällt der Graph von
deutlich langsamer ab.
(2)
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
- Wende das notwendige Kriterium an, indem du
setzt und so mögliche Extremstellen bestimmst.
- Überprüfe das hinreichende Kriterium durch Einsetzen in die zweite Ableitungsfunktion.
- Berechne die
-Koordinate des Tiefpunkts durch Einsetzen in
.
- Berechne die Funktionswerte an den Intervallgrenzen um mögliche Randextrema auszuschließen.
Du kannst die Ableitungen zunächst in deinem CAS definieren. Den Befehl dazu findest du wie folgt:
 setzen und so mögliche Extremstellen bestimmen:
$x_1 =-10,5
setzen und so mögliche Extremstellen bestimmen:
$x_1 =-10,5 \quad
\quad x_2 = 0
x_2 = 0  \quad
\quad x_3= 7,5$
x_3= 7,5$
menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
Mit dem solve-Befehl kannst du dann 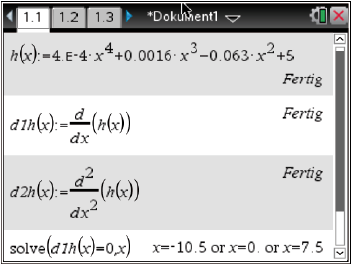 Abb. 3: Notwendiges Kriterium
Abb. 3: Notwendiges Kriterium
Einsetzen von  in
in  liefert:
liefert:
![\(\begin{array}[t]{rll}
h‘‘(x_2)&=&h‘‘(7,5) \\[5pt]
&=& 0,216 > 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c919a70d0cd285263eb9377dafbfd41357e5d50887969310795c9eb9e614bfe0?color=5a5a5a) An der Stelle
An der Stelle  besitzt der Graph von
besitzt der Graph von  einen lokalen Tiefpunkt.
einen lokalen Tiefpunkt.
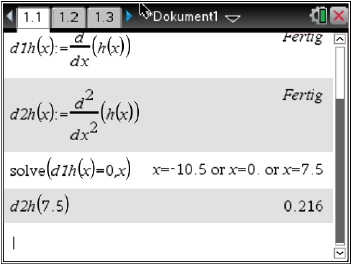 Abb. 4: Hinreichendes Kriterium
Abb. 4: Hinreichendes Kriterium
(3)
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
c)
(1)
(2)
Dies kannst du wie oben mit deinem CAS lösen.
Also ist  und
und  . Eine Gleichung der Modellierungsgerade lautet:
. Eine Gleichung der Modellierungsgerade lautet:

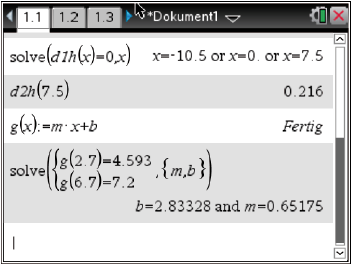 Abb. 5: Hinreichendes Kriterium
Abb. 5: Hinreichendes Kriterium
(3)
besitzt dieselbe Steigung, wie der Graph von
im Punkt
verläuft ebenfalls durch den Punkt
d)
(1)
Den Befehl für ein Integral findest du in deinem CAS wie folgt:

menu  4: Analysis
4: Analysis  3: Integral
3: Integral
Du erhältst folgendes Ergebnis:
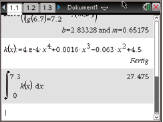 Abb. 6: Integralberechnung
Abb. 6: Integralberechnung
(2)
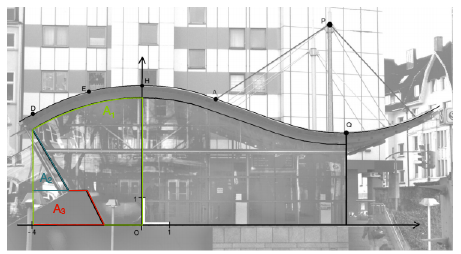 Abb. 7: Aufteilung der Fläche
Abb. 7: Aufteilung der Fläche
: Der Inhalt der blauen dreieckigen Fläche
: Der Inhalt der roten trapezförmigen Fläche
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
(1)
(2)
Den Befehl für ein Gleichungssystem findest du wie folgt:
keyboard  Math1
Math1
Dann erhältst du folgendes Ergebnis:
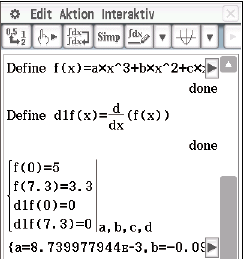 Abb. 1: Funktionsgleichung bestimmen
Abb. 1: Funktionsgleichung bestimmen
b)
(1)
Betrachte beide Graphen und notiere zunächst alle Unterschiede oder auffälligen Gemeinsamkeiten der beiden Graphen. Anschließend kannst du entscheiden, welcher Verlauf besser zu dem der Dachoberkante passt.
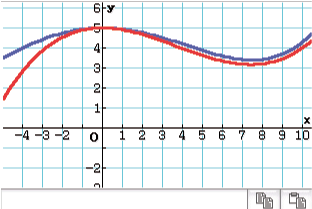 Abb. 2: Vergleich der Graphen
Abb. 2: Vergleich der Graphen
- Beide Graphen besitzen den Hochpunkt
.
- Für
haben beide einen ähnlichen Verlauf, wobei der Graph von
etwas oberhalb des Graphen von
liegt.
- Nur im Bereich
unterscheidet sich der Verlauf etwas deutlicher: Für kleiner werdende
-Werte fällt der Graph von
deutlich langsamer ab.
(2)
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
- Wende das notwendige Kriterium an, indem du
setzt und so mögliche Extremstellen bestimmst.
- Überprüfe das hinreichende Kriterium durch Einsetzen in die zweite Ableitungsfunktion.
- Berechne die
-Koordinate des Tiefpunkts durch Einsetzen in
.
- Berechne die Funktionswerte an den Intervallgrenzen um mögliche Randextrema auszuschließen.
Du kannst die Ableitungen zunächst in deinem CAS definieren. Den Befehl dazu findest du wie folgt:
 setzen und so mögliche Extremstellen bestimmen:
$x_1 =-10,5
setzen und so mögliche Extremstellen bestimmen:
$x_1 =-10,5 \quad
\quad x_2 = 0
x_2 = 0  \quad
\quad x_3= 7,5$
x_3= 7,5$
keyboard  Math2
Math2
Mit dem solve-Befehl kannst du dann 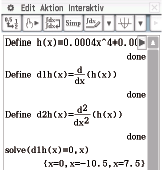 Abb. 3: Notwendiges Kriterium
Abb. 3: Notwendiges Kriterium
Einsetzen von  in
in  liefert:
liefert:
![\(\begin{array}[t]{rll}
h‘‘(x_2)&=&h‘‘(7,5) \\[5pt]
&=& 0,216 > 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c919a70d0cd285263eb9377dafbfd41357e5d50887969310795c9eb9e614bfe0?color=5a5a5a) An der Stelle
An der Stelle  besitzt der Graph von
besitzt der Graph von  einen lokalen Tiefpunkt.
einen lokalen Tiefpunkt.
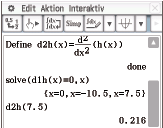 Abb. 4: Hinreichendes Kriterium
Abb. 4: Hinreichendes Kriterium
(3)
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
c)
(1)
(2)
Dies kannst du wie oben mit deinem CAS lösen.
Also ist  und
und  . Eine Gleichung der Modellierungsgerade lautet:
. Eine Gleichung der Modellierungsgerade lautet:

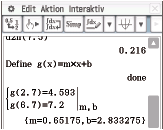 Abb. 5: Hinreichendes Kriterium
Abb. 5: Hinreichendes Kriterium
(3)
besitzt dieselbe Steigung, wie der Graph von
im Punkt
verläuft ebenfalls durch den Punkt
d)
(1)
Den Befehl für ein Integral findest du in deinem CAS wie folgt:

keyboard  Math2
Math2
Du erhältst folgendes Ergebnis:
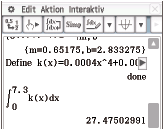 Abb. 6: Integralberechnung
Abb. 6: Integralberechnung
(2)
 Abb. 7: Aufteilung der Fläche
Abb. 7: Aufteilung der Fläche
: Der Inhalt der blauen dreieckigen Fläche
: Der Inhalt der roten trapezförmigen Fläche
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.