Aufgabe 5
Ein Unternehmen verkauft Fitnessarmbänder. Die momentane Änderungsrate des Absatzes kann modellhaft mithilfe der in 
definierten Funktion 
mit 
beschrieben werden. Dabei ist 
die seit der Produkteinführung vergangene Zeit in Monaten und 
die momentane Änderungsrate des Absatzes in Stück pro Monat.
Gleichzeitig mit der Einführung des Fitnessarmbands brachte das Unternehmen eine Smartwatch auf den Markt. Die momentane Änderungsrate des Absatzes der Smartwatch in Stück pro Monat lässt sich im Modell mithilfe der in definierten Funktion 
mit 
beschreiben.
a)
(1)
Bestimme rechnerisch den Zeitpunkt, zu dem die momentane Änderungsrate des Absatzes den größten Wert erreicht, und gib diesen Wert an.
(2)
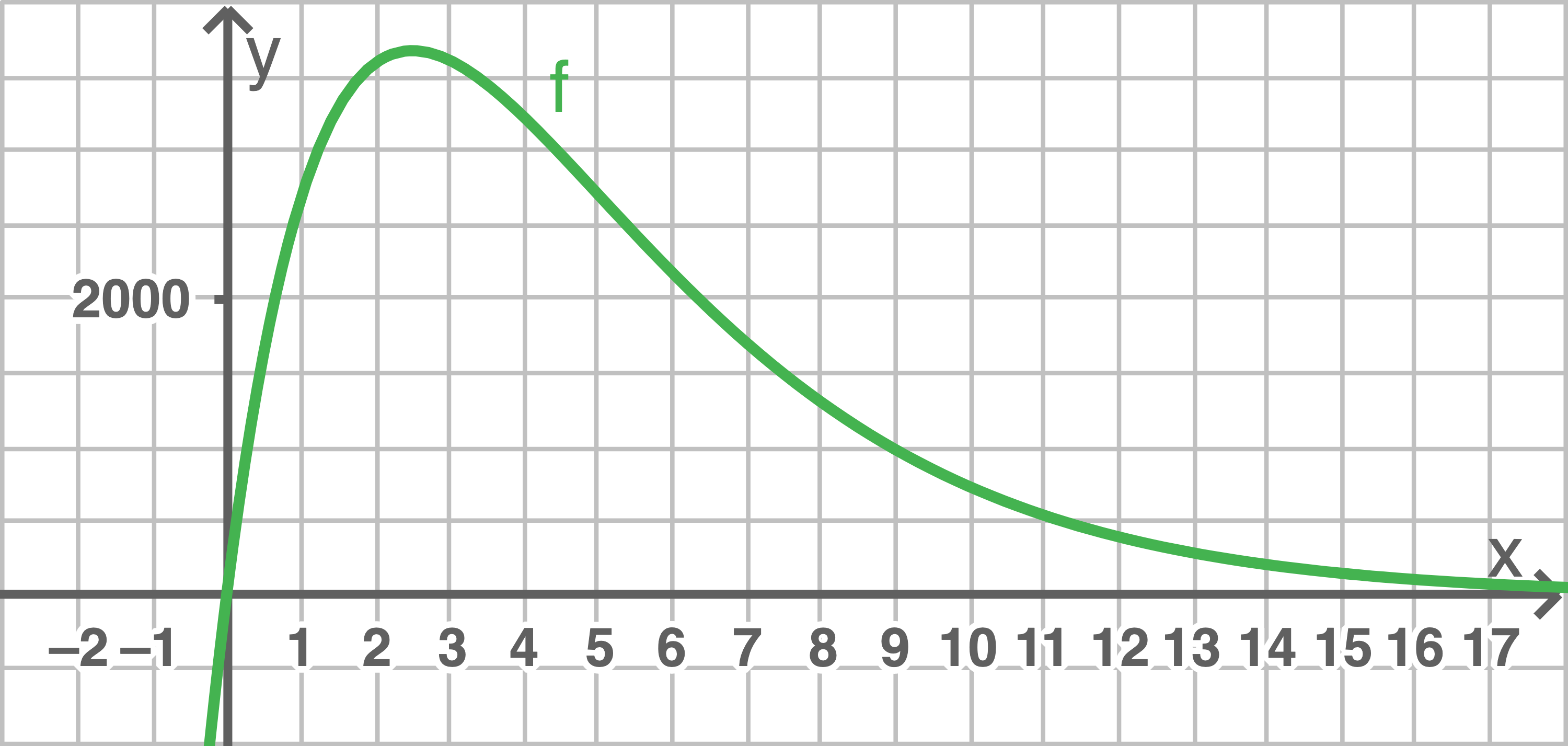
Zeichne den Graphen von für 
Zeichne in deine Abbildung diejenigen Punkte des Graphen ein, die zu einer momentanen Änderungsrate des Absatzes in Höhe von 1000 Stück pro Monat gehören.
(3)
Im Zeitraum, der mit der Produkteinführung beginnt und 18 Monate später endet, gibt es einen Zeitpunkt, zu dem die momentane Änderungsrate des Absatzes am stärksten zunimmt, und einen Zeitpunkt, zu dem sie am stärksten abnimmt. Zur Bestimmung dieser beiden Zeitpunkte wurden folgende Berechnungen durchgeführt:
Erläutere diese Berechnungen. Gib die beiden gesuchten Zeitpunkte an und begründe deine Angabe ohne weitere Rechnung.
(4 + 3 + 6 Punkte)
b)
(1)
Vergleiche die momentane Änderungsrate des Absatzes für das Fitnessarmband und die Smartwatch fünft Monate nach Produkteinführung.
(2)
Ermittle die Anzahl der im ersten Jahr nach Produkteinführung insgesamt verkauften Smartwatches.
(3)
Untersuche im Modell, ob es einen Zeitpunkt gibt, zu dem die Anzahl der seit der Produkteinführung verkauften Fitnessarmbänder mit der Anzahl der seit der Produkteinführung verkauften Smartwatches übereinstimmt.
Gib gegebenenfalls diesen Zeitpunkt an.
(2 + 2 + 3 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/6281c107916a78d647bb16409e7052e381096a80855f844947cf57b4b96df262?color=5a5a5a)
Nach dem Satz vom Nullprodukt gilt:
![\(\begin{array}[t]{rll}
1-0,4\cdot x&=& 0 &\quad \scriptsize \mid\; -1 \\[5pt]
-0,4\cdot x&=& -1 &\quad \scriptsize \mid\; :(-0,4) \\[5pt]
x&=&2,5
\end{array}\)](https://mathjax.schullv.de/65c0e5a6aa5198d09165d77cf8dbb388007f2349de83e199cc2bbac159687142?color=5a5a5a)
Es gilt 
, deshalb ist 
die einzige Extremstelle.
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
Nach der Produktregel ist 
3. Schritt: 
ermitteln
Die momentane Änderungsrate des Absatzes erreicht zweieinhalb Monate nach Produkteinführung mit ungefähr 
Stück pro Monat den größten Wert.
(2)
(3)
Die gesuchten Zeitpunkte sind durch die globalen Extremstellen der Ableitungsfunktion 
im Intervall ![\([0;18]\)](https://mathjax.schullv.de/e8e9fe9ed19539c81417a22651f2286708601f9b50fd50615a26fa465a3ca531?color=5a5a5a)
gegeben, bei denen es sich um lokale Extremstellen oder Randstellen handeln kann.
Mit der Berechnung werden zunächst die lokalen Extremstellen von ermittelt: 
ist die einzige Nullstelle der Funktion 
und damit die einzige mögliche lokale Extremstelle von 
Da zusätzlich 
gilt, ist eine lokale Minimalstelle von . 
ist als einzige lokale Extremstelle von auch die globale Minimalstelle von . Da außerdem der Graph von an der Stelle fällt, gilt: Fünf Monate nach der Produkteinführung nimmt die momentane Änderungsrate des Absatzes am stärksten ab. Da der Graph von an der Randstelle 
steigt und an der Randstelle 
fällt, gilt 
und 
Daher ist die globale Maximalstelle von 
Die momentane Änderungsrate des Absatzes nimmt zum Zeitpunkt der Produkteinführung am stärksten zu.
b)
(1)
Mit dem CAS ergibt sich:
Somit ist fünf Monate nach Produkteinführung die momentane Änderungsrate des Absatzes für das Fitnessarmband kleiner als für die Smartwatch.
(2)
Mit dem CAS ergibt sich:
Im ersten Jahr nach der Produkteinführung werden ungefähr 
Smartwatches verkauft.
(3)
Die Anzahl an verkauften Geräten kann jeweils mit einem Integral berechnet werden:
Anzahl der verkauften Smartwatches bis zum Zeitpunkt 
Anzahl der verkauften Fitnessarmbänder bis zum Zeitpunkt 
![\(\begin{array}[t]{rll}
A_S&=& A_F \\[5pt]
\displaystyle\int_{0}^{t}f(x)\;\mathrm dx&=& \displaystyle\int_{0}^{t}g(x)\;\mathrm dx
\end{array}\)](https://mathjax.schullv.de/4a373c1d73210dc432a150f394dac82486a9339e681da5d3a663a0a277d6519b?color=5a5a5a)
Für 
folgt mit dem solve-Befehl des CAS 
Etwa viereinhalb Monate nach Produkteinführung stimmt die Anzahl der seit der Produkteinführung verkauften Fitnessarmbänder mit der Anzahl der seit der Produkteinführung verkauften Smartwatches überein.