C1 - Lineare Algebra, Analytische Geometrie
Ein neu geplantes Mehrfamilienhaus soll  breit,
breit,  lang und inklusive Dach
lang und inklusive Dach  hoch werden.
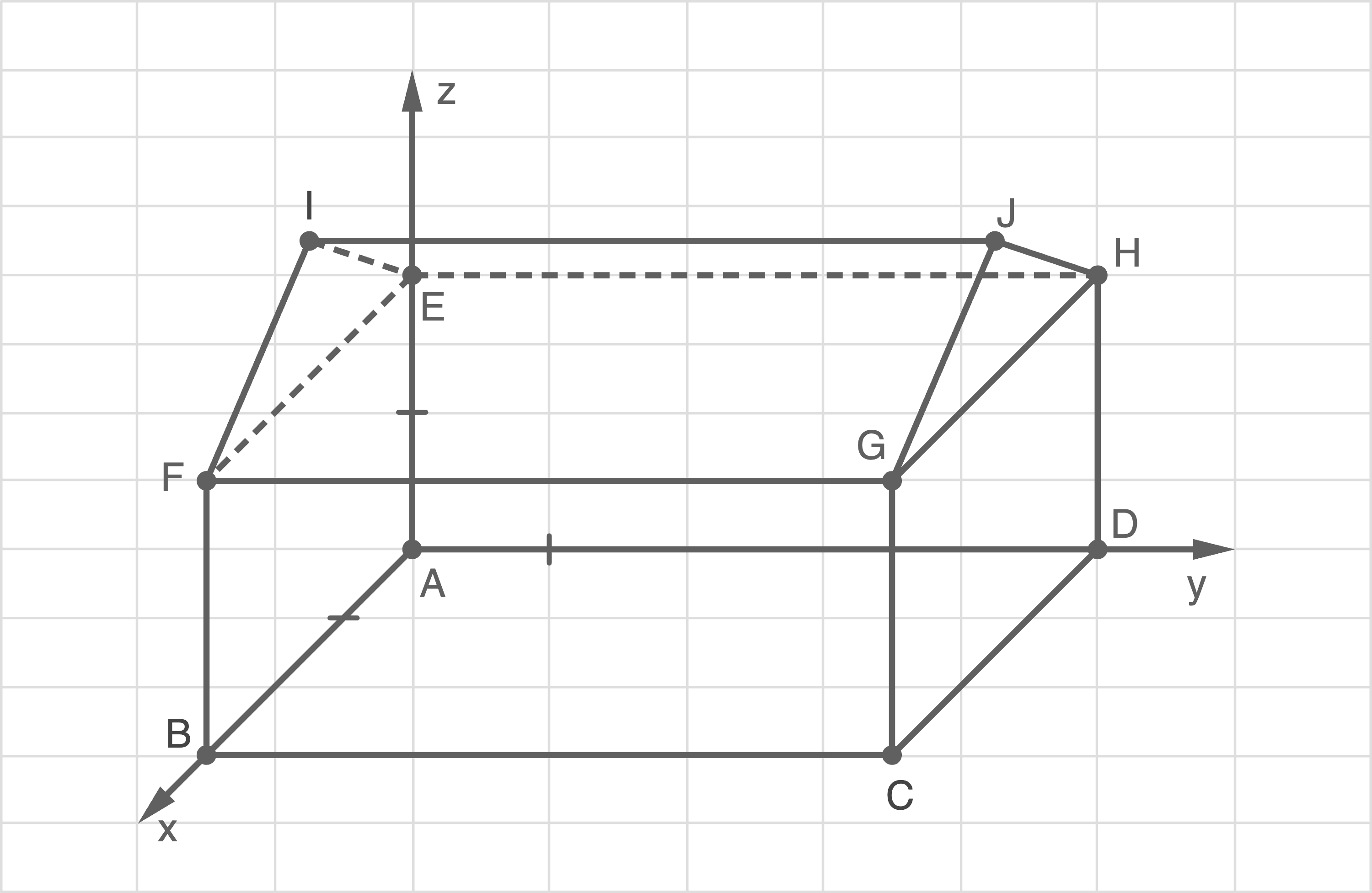
Die Abbildung zeigt eine Darstellung des Hauses im Koordinatensystem.
Der Erdboden wird durch die
hoch werden.
Die Abbildung zeigt eine Darstellung des Hauses im Koordinatensystem.
Der Erdboden wird durch die  -
- -Ebene beschrieben. In dieser Ebene liegen die Eckpunkte
-Ebene beschrieben. In dieser Ebene liegen die Eckpunkte 

 und
und  des rechteckigen Hausbodens. Der Punkt
des rechteckigen Hausbodens. Der Punkt  hat die Koordinaten
hat die Koordinaten  Der Dachfirst
Der Dachfirst  verläuft horizontal und mittig über der Dachbodenfläche
verläuft horizontal und mittig über der Dachbodenfläche 
1.1
Gib die Koordinaten der Punkte  und
und  an.
Beschrifte die Achsen in der Abbildung mit einer geeigneten Skalierung.
an.
Beschrifte die Achsen in der Abbildung mit einer geeigneten Skalierung.
(5 BE)
1.2
Gib eine Parametergleichung der Ebene  an, in der die Dachfläche
an, in der die Dachfläche  liegt, und bestimme eine Koordinatengleichung dieser Ebene.
liegt, und bestimme eine Koordinatengleichung dieser Ebene.
 Zur Kontrolle:
Zur Kontrolle:  ist eine mögliche Koordinatengleichung der Ebene.
ist eine mögliche Koordinatengleichung der Ebene. ![\(\big]\)](https://mathjax.schullv.de/0c6dff9ed6a80b0cc013679b53aff551dd11abb4691ba32076d10b15d6195a5d?color=5a5a5a)
(6 BE)
1.3
Berechne den Flächeninhalt der gesamten Dachfläche des Hauses.
(3 BE)
1.4
Berechne das Volumen des Mehrfamilienhauses.
(3 BE)
1.5
Damit das Dach für die geplante Installation einer Photovoltaikanlage geeignet ist, sollte die Dachneigung zwischen 30 und 35 Grad betragen.
In diesem Sachzusammenhang wird folgende Rechnung durchgeführt:


 Erläutere den Ansatz in Zeile
Erläutere den Ansatz in Zeile  und den Rechenschritt in Zeile
und den Rechenschritt in Zeile  Berechne den Winkel
Berechne den Winkel  Deute das Ergebnis für
Deute das Ergebnis für  im Sachzusammenhang.
im Sachzusammenhang.
Auf dem Nachbargrundstück steht eine
(1)
(2)
(4 BE)
1.6
Prüfe, ob der Schatten der Tannenspitze zu diesem Zeitpunkt auf die Dachfläche  trifft.
trifft.
(5 BE)
2
Im Garten des Hauses soll ein Blumenbeet angelegt werden. Dafür sollen Pflanzen dreier Pflanzengattungen gekauft werden.
Eine Pflanze der Gattung Sonnenhut kostet  eine der Gattung Phlox
eine der Gattung Phlox  und eine der Gattung Malve
und eine der Gattung Malve  Es sollen genau
Es sollen genau  Pflanzen für insgesamt
Pflanzen für insgesamt  gekauft werden. Darunter sollen doppelt so viele Pflanzen der Gattung Sonnenhut wie Pflanzen der Gattung Malve sein.
gekauft werden. Darunter sollen doppelt so viele Pflanzen der Gattung Sonnenhut wie Pflanzen der Gattung Malve sein.
2.1
Mit Hilfe der Informationen im Text kann das folgende lineare Gleichungssystem aufgestellt werden:
 Gib eine Definition der verwendeten Variablen an.
Erläutere die Bedeutung der einzelnen Gleichungen im Sachzusammenhang.
Gib eine Definition der verwendeten Variablen an.
Erläutere die Bedeutung der einzelnen Gleichungen im Sachzusammenhang.
(4 BE)
2.2
Das lineare Gleichungssystem besitzt ohne Beachtung des Sachzusammenhangs unendlich viele Lösungen.
Berechne diese Lösungen.
(5 BE)
2.3
Eine mögliche Darstellung aller Lösungen des linearen Gleichungssystems lautet:

2.3.1
Um eine mögliche Bepflanzung des Beetes darzustellen, müssen 
 und
und  nichtnegative ganzzahlige Werte annehmen.
Untersuche, welche Werte
nichtnegative ganzzahlige Werte annehmen.
Untersuche, welche Werte  unter dieser Bedingung annehmen kann.
unter dieser Bedingung annehmen kann.
(3 BE)
2.3.2
Gesucht ist die Bepflanzung mit der maximal möglichen Anzahl der Pflanzen der Gattung Sonnenhut.
Bestimme die Anzahlen der Pflanzen der Gattung Sonnenhut, Phlox und Malve für diese Bepflanzung.
(2 BE)
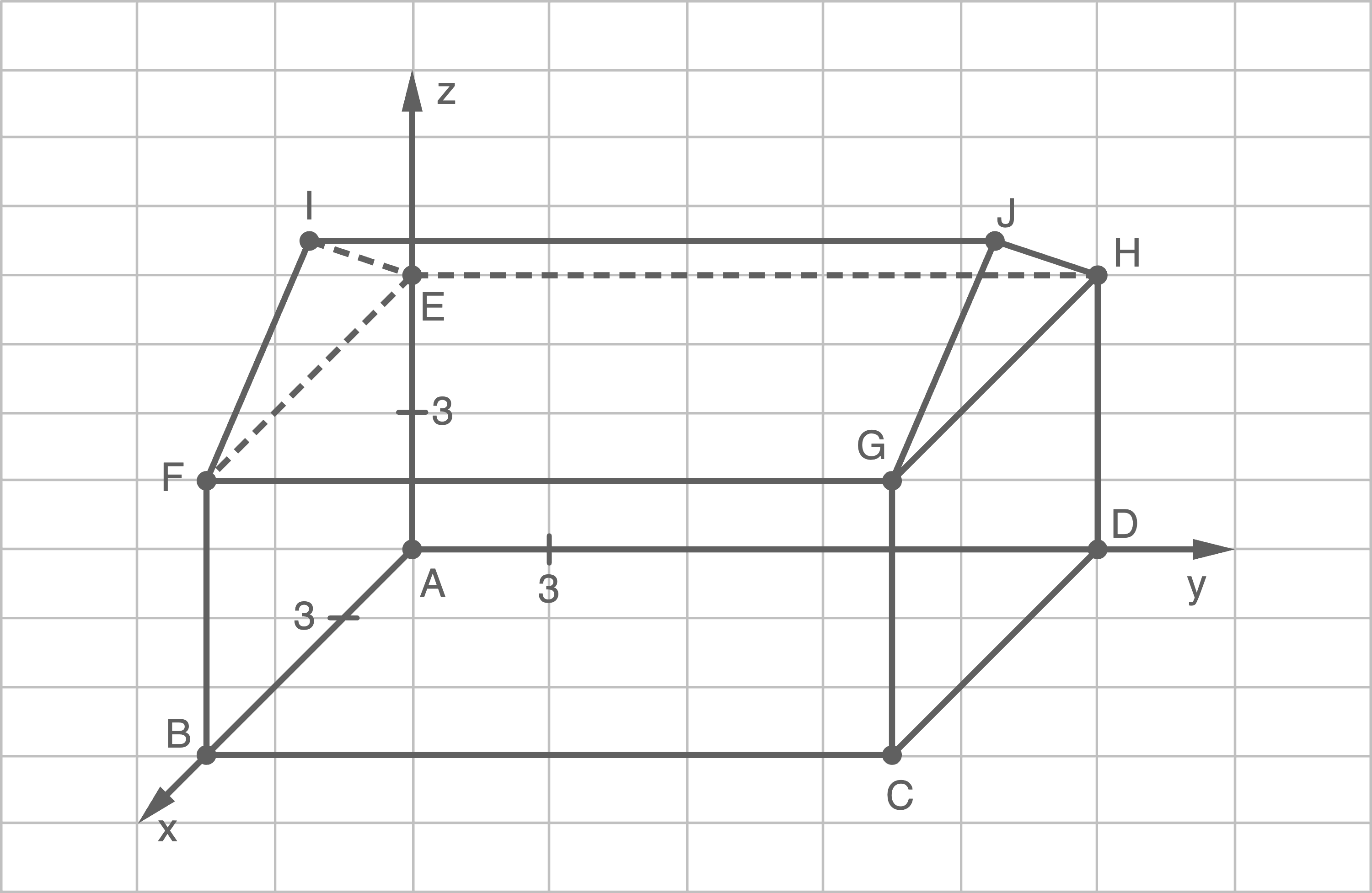
1.1
Koordinaten angeben
Mit den Angaben aus der Aufgabenstellung folgt:


 Achsen beschriften
Achsen beschriften

1.2
Parametergleichung angeben
Koordinatengleichung bestimmen
Ein Normalenvektor der Ebene  ergibt sich aus dem Kreuzprodukt der Spannvektoren:
ergibt sich aus dem Kreuzprodukt der Spannvektoren:
![\(\begin{array}[t]{rll}
\overrightarrow{n} &=& \overrightarrow{FG} \times \overrightarrow{FJ} \\[5pt]
&=&\pmatrix{0\\15\\0} \times \pmatrix{-4,5\\ 15\\3} \\[5pt]
&=& \pmatrix{15\cdot 3 - 0\cdot 15 \\ 0\cdot (-4,5) - 0\cdot 3 \\ 0\cdot 15 - 15\cdot (-4,5) } \\[5pt]
&=& \pmatrix{45\\0\\67,5} \\[5pt]
&=& 22,5\cdot \pmatrix{2\\0\\3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d0013d6fa513af6529ec1655d6ee393f3c27ff331036af0ba1669223fa9d51c6?color=5a5a5a) Einsetzen in die allgemeine Koordinatengleichung liefert:
Einsetzen in die allgemeine Koordinatengleichung liefert:
![\(\begin{array}[t]{rll}
T: \; 2\cdot x+0\cdot y+3\cdot z&=& d & \\[5pt]
2x+3z&=& d
\end{array}\)](https://mathjax.schullv.de/0196e3cb89a2b74a7b0039ceb90682f21e66f7bc8a72d9cab563f590ff2635d9?color=5a5a5a) Einsetzen der Koordinaten von
Einsetzen der Koordinaten von 
![\(\begin{array}[t]{rll}
T:\quad \quad 2x +3z &=& d &\quad \scriptsize \mid\; F(9\mid 0 \mid 6) \\[5pt]
2\cdot 9 + 3\cdot 6&=& d \\[5pt]
36 &=& d
\end{array}\)](https://mathjax.schullv.de/21d62b02b11e9fdb75b11c4592c0bbce62422ebc9ff742e2d92a75b0618f8934?color=5a5a5a) Eine Gleichung von
Eine Gleichung von  in Koordinatenform lautet also:
in Koordinatenform lautet also:

1.3
Da beide Dachflächen identisch und rechteckig sind, kann der gesuchte Flächeninhalt wie folgt berechnet werden:
Die gesamte Dachfläche ist folglich ca.  groß.
groß.
1.4
1. Schritt: Volumen des Dachs berechnen
Das Dach hat die Form eines Prismas mit dreiseitiger Grundfläche.
Die dreieckige Grundfläche  besitzt die Grundseite
besitzt die Grundseite  mit einer Länge von
mit einer Länge von  die Breite des Hauses, und eine Höhe von
die Breite des Hauses, und eine Höhe von  die Höhe des Dachbodens.
Für die Grundfläche gilt also:
die Höhe des Dachbodens.
Für die Grundfläche gilt also:
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2}\cdot 9 \,\text{m} \cdot 3\,\text{m}& \\[5pt]
&=& 13,5 \,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/69e5ed77103b338fd2379b58adc811b605591c593efdfdb268533806a5711588?color=5a5a5a) Die Höhe des Prismas entspricht der Länge des Hauses und beträgt somit
Die Höhe des Prismas entspricht der Länge des Hauses und beträgt somit  Es folgt also:
Es folgt also:
![\(\begin{array}[t]{rll}
V_{\text{Dach}}&=& 13,5 \,\text{m}^2 \cdot 15\,\text{m} \\[5pt]
&=& 202,5\,\text{m}^3
\end{array}\)](https://mathjax.schullv.de/d5211c8acc8b85f26381306f680215a9621b0c2e74fe1fb58b8e9d6ef2c4f449?color=5a5a5a) 2. Schritt: Volumen des Hauses berechnen
Der untere Teil des Hauses hat die Form eines Quaders mit einer Länge von
2. Schritt: Volumen des Hauses berechnen
Der untere Teil des Hauses hat die Form eines Quaders mit einer Länge von  einer Breite von
einer Breite von  und einer Höhe von
und einer Höhe von 
![\(\begin{array}[t]{rll}
V_{\text{Quader}}&=& 15\,\text{m}\cdot 9\,\text{m} \cdot 6\,\text{m} \\[5pt]
&=& 810\,\text{m}^3
\end{array}\)](https://mathjax.schullv.de/d158277177eee29e0236798bff8c58e9c9b6dcb8807e4e60967b0d5e5f0166d5?color=5a5a5a) 3. Schritt: Gesamtvolumen berechnen
3. Schritt: Gesamtvolumen berechnen
![\(\begin{array}[t]{rll}
V &=& V_{\text{Dach}} + V_{\text{Quader}} \\[5pt]
&=& 202,5\,\text{m}^3 + 810\,\text{m}^3 \\[5pt]
&=& 1012,5\,\text{m}^3
\end{array}\)](https://mathjax.schullv.de/4d21256ee5707e409e4b216d13aa8dead14fdfa992e8c54e133d00bd57378bbc?color=5a5a5a) Das Gesamtvolumen des Hauses beträgt somit
Das Gesamtvolumen des Hauses beträgt somit 
1.5
Ansatz  erläutern
erläutern
 entspricht dem Verbindungsvektor
entspricht dem Verbindungsvektor 
 entspricht dem Verbindungsvektor
entspricht dem Verbindungsvektor  Rechenschritt
Rechenschritt  erläutern
In Schritt (2) wird der Winkel zwischen den beiden Vektoren
erläutern
In Schritt (2) wird der Winkel zwischen den beiden Vektoren  und
und  bestimmt, welcher der Dachneigung entspricht.
Winkel
bestimmt, welcher der Dachneigung entspricht.
Winkel  berechnen
Der Winkel
berechnen
Der Winkel  ist folglich ca.
ist folglich ca.  groß.
Ergebnis deuten
Die Dachneigung beträgt ca.
groß.
Ergebnis deuten
Die Dachneigung beträgt ca.  und somit zwischen
und somit zwischen  und
und  Damit ist das Dach in Bezug auf die Dachneigung für die Installation einer Photovoltaikanlage geeignet.
Damit ist das Dach in Bezug auf die Dachneigung für die Installation einer Photovoltaikanlage geeignet.
1.6
Da die Tanne im Punkt  steht, befindet sich ihre Spitze im Punkt
steht, befindet sich ihre Spitze im Punkt  Der Lichtstrahl, der auf die Tannenspitze trifft und entlang welchem folglich auch der Schatten auf das Dach geworfen wird, kann durch die Gerade
Der Lichtstrahl, der auf die Tannenspitze trifft und entlang welchem folglich auch der Schatten auf das Dach geworfen wird, kann durch die Gerade  beschrieben werden:
1. Schritt: Geradengleichung aufstellen
beschrieben werden:
1. Schritt: Geradengleichung aufstellen
![\(\begin{array}[t]{rll}
g:\, \overrightarrow{x} &=& \overrightarrow{OS} + t\cdot \overrightarrow{v}\\[5pt]
&=& \pmatrix{30,75\\ 6\\13,5 } + t\cdot \pmatrix{-2\\0\\-0,5} \\[5pt]
&=& \pmatrix{30,75-2t\\ 6\\13,5-0,5t }
\end{array}\)](https://mathjax.schullv.de/24e46def81ab6510d0d1e43d656ec70b4e996bf338fc85a4f00b1b35473e786e?color=5a5a5a) 2. Schritt: Schnittpunkt bestimmen
Der Schattenpunkt der Tannenspitze auf dem Dach entspricht dem Schnittpunkt der Geraden
2. Schritt: Schnittpunkt bestimmen
Der Schattenpunkt der Tannenspitze auf dem Dach entspricht dem Schnittpunkt der Geraden  mit der Ebene
mit der Ebene  Einsetzen des allgemeinen Geradenpunkts von
Einsetzen des allgemeinen Geradenpunkts von  in die Koordinatengleichung von
in die Koordinatengleichung von  aus Aufgabe 1.2 liefert:
Der Schnittpunkt
aus Aufgabe 1.2 liefert:
Der Schnittpunkt  folgt also mit:
folgt also mit:
![\(\begin{array}[t]{rll}
\overrightarrow{OS](https://mathjax.schullv.de/68791df0bd0934b9ca8b41d2b16cccb368b965a8dbe073ea152ee11d9d03bc41?color=5a5a5a) Unter Verwendung der Abbildung zeigt sich, dass der Punkt genau dann auf der Dachfläche des Hauses liegt, wenn seine
Unter Verwendung der Abbildung zeigt sich, dass der Punkt genau dann auf der Dachfläche des Hauses liegt, wenn seine  -Koordinate zwischen 4,5 und 9 und die
-Koordinate zwischen 4,5 und 9 und die  -Koordinate zwischen 0 und 15 liegt.
Da der Schnittpunkt die Koordinaten
-Koordinate zwischen 0 und 15 liegt.
Da der Schnittpunkt die Koordinaten  besitzt, trifft der Schatten der Tannenspitze also auf die Dachfläche.
besitzt, trifft der Schatten der Tannenspitze also auf die Dachfläche.
2.1
Definition angeben
 Anzahl der Pflanzen der Gattung Sonnenhut
Anzahl der Pflanzen der Gattung Sonnenhut
 Anzahl der Pflanzen der Gattung Phlox
Anzahl der Pflanzen der Gattung Phlox
 Anzahl der Pflanzen der Gattung Malve
Bedeutung erläutern
Anzahl der Pflanzen der Gattung Malve
Bedeutung erläutern



Die Anzahl der Pflanzen der Gattung Sonnenhut ist doppelt so groß wie die Anzahl der Pflanzen der Gattung Malve.
Die Gesamtanzahl der Pflanzen beträgt 
Die Gesamtkosten der Pflanzen betragen 
2.2
Wegen  folgt, dass das Gleichungssystem unendlich viele Lösungen hat.
Mit
folgt, dass das Gleichungssystem unendlich viele Lösungen hat.
Mit  folgt nun also:
folgt nun also:
 Aus
Aus  folgt:
folgt:
![\(\begin{array}[t]{rll}
x_S -2t&=& 0&\quad \scriptsize \mid\; +2t \\[5pt]
x_S&=& 2t \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b2fb0e0f67b82fb1f0925fdcbd870a3bb98b9ece870857dd05bf127cefcec576?color=5a5a5a) Einsetzen in
Einsetzen in  liefert:
Ein Lösungsvektor des Gleichungssystems ist somit gegeben durch
liefert:
Ein Lösungsvektor des Gleichungssystems ist somit gegeben durch 
2.3.1
Die Lösungen werden wie folgt angegeben:
 Die Einträge
Die Einträge  und
und  sind genau dann ganzzahlig, wenn auch
sind genau dann ganzzahlig, wenn auch  ganzzahlig ist.
Für
ganzzahlig ist.
Für  folgt:
folgt:
![\(\begin{array}[t]{rll}
x_S &\geq& 0 \\[5pt]
2t &\geq& 0 &\quad \scriptsize \mid\; :2 \\[5pt]
t &\geq & 0
\end{array}\)](https://mathjax.schullv.de/d7b914406da6557f222a0d14e1ea2346df6fb2435ebdf62b105e7b6f0eb461f4?color=5a5a5a) Für
Für  folgt:
folgt:
![\(\begin{array}[t]{rll}
x_P&\geq & 0 \\[5pt]
25-3t &\geq& 0 &\quad \scriptsize \mid\;-25 \\[5pt]
-3t&\geq& -25 &\quad \scriptsize \mid\;:(-3) \\[5pt]
t&\leq& \dfrac{25}{3}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/ca583a884e75b33e838b9f3bac6ffd059205e571f3809017be510a4852ed6c82?color=5a5a5a) Da nur ganzzahlige Werte für
Da nur ganzzahlige Werte für  zugelassen sind, gilt
zugelassen sind, gilt 
 kann unter der gegebenen Bedingung also alle Werte zwischen 0 und 8 annehmen.
kann unter der gegebenen Bedingung also alle Werte zwischen 0 und 8 annehmen.
2.3.2
Die Anzahl der Pflanzen der Gattung Sonnenhut wird durch  beschrieben. Je größer also
beschrieben. Je größer also  ist, desto größer ist
ist, desto größer ist  Es gilt
Es gilt  Die maximal mögliche Anzahl der Pflanzen der Gattung Sonnenhut ergibt sich also mit
Die maximal mögliche Anzahl der Pflanzen der Gattung Sonnenhut ergibt sich also mit  zu:
zu:
 Für die anderen beiden Gattungen gilt:
Für die anderen beiden Gattungen gilt:

 Es müssen also 16 Sonnenhut-Pflanzen, eine Phlox-Pflanze und 8 Malven-Pflanzen gekauft werden, damit alle Bedingungen erfüllt sind.
Es müssen also 16 Sonnenhut-Pflanzen, eine Phlox-Pflanze und 8 Malven-Pflanzen gekauft werden, damit alle Bedingungen erfüllt sind.