C1 - Lineare Algebra, Analytische Geometrie

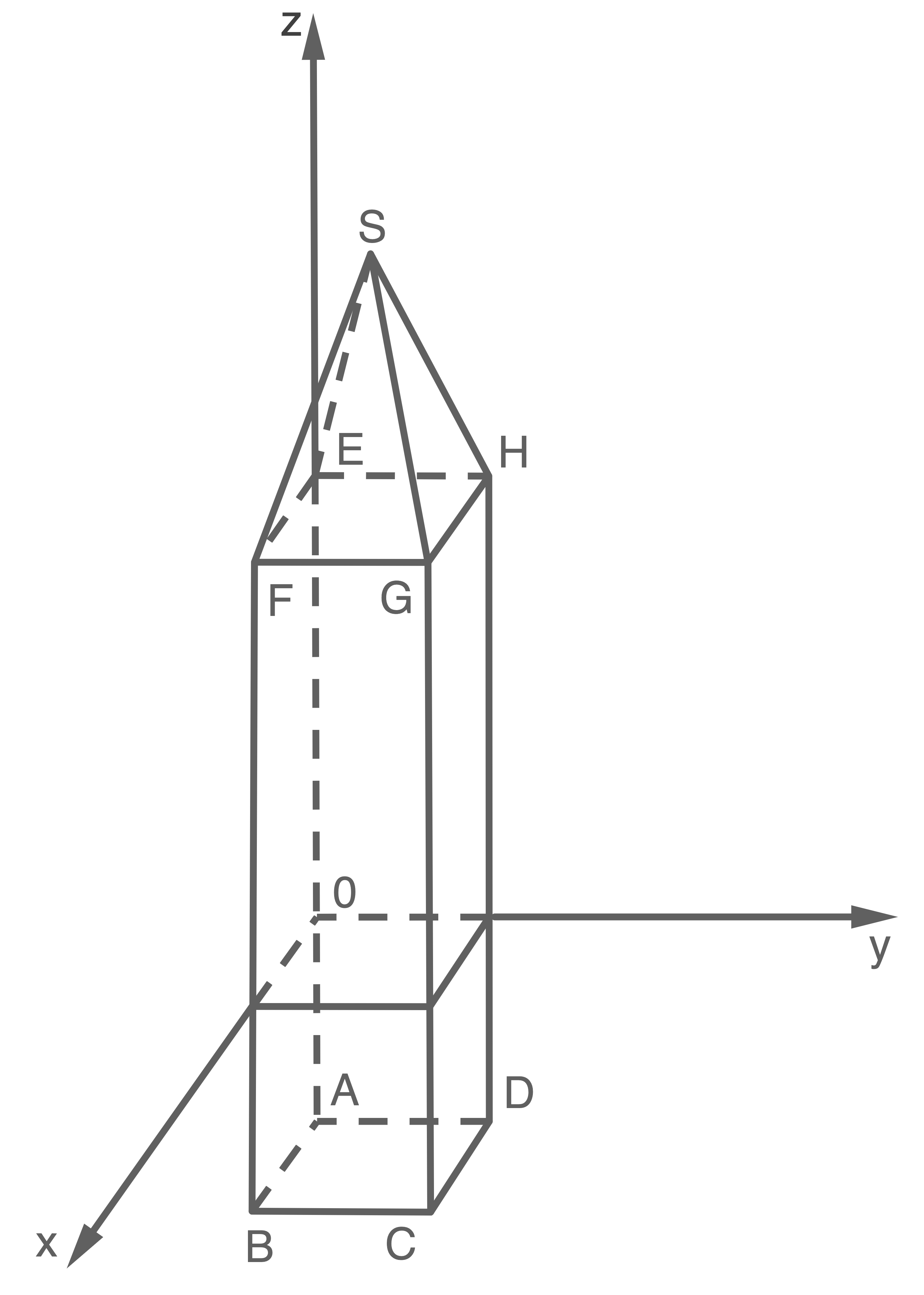
In Südtirol ragt im aufgestauten Reschensee ein versunkener Kirchturm empor

Zur Beschreibung des Kirchturms wird ein räumliches Koordinatensystem gewählt. Die Wasseroberfläche liegt in der $x$ - $y$ -Ebene. Eine Einheit in dem Koordinatensystem entspricht einem Meter.

Der Kirchturm besteht aus einem $22\,\text{m}$ hohen, quaderförmigen unteren Teil mit $36 \,\text{m}^2$ großer quadratischer Grundfläche. Darüber befindet sich ein $9\,\text{m}$ hohes, symmetrisches Dach in Form einer Pyramide. Je nach Wasserstand ragt der Turm unterschiedlich weit aus dem Reschensee empor.

Ein alter, steinerner Kirchturm, der aus einem klaren Gewässer ragt, umgeben von Bergen und Wolken.

1.1

Zu einem bestimmten Zeitpunkt befindet sich die Grundfläche $ABCD$ des Turmes $7\,\text{m}$ unter der Wasseroberfläche. Die Kante $AE$ liegt auf der $z$ -Achse.

Gib die Koordinaten der Punkte $A,B,G,H$ und $S$ in Material 2 an.

(5 BE)

1.2

Für eine Restaurierung im Jahr 2009 wurde das Dach erneuert.

Berechne den Flächeninhalt der Dachfläche.

(4 BE)

Zur Untersuchung des Reschensees wurden zwei Tauchroboter $R1$ und $R2$ eingesetzt, die sich mit konstanten Geschwindigkeiten auf geradlinigen Bahnen unter Wasser fortbewegen und Daten an eine Forschungsstation senden. Im Verlauf des ersten Tauchgangs werden folgende Ortungsdaten gesendet:

Ortungsdaten von $R1:$

Zum Zeitpunkt $t_1:P_1(24\mid 8\mid -1)$

Zum Zeitpunkt $t_2:P_2(20\mid 5\mid -3)$

Ortungsdaten von $R_2:$

Zum Zeitpunkt $t_1: Q_1(15\mid 0\mid -5,5)$

Zum Zeitpunkt $t_2:Q_2(9\mid -2\mid -8,5)$

2.1

Bestimme die Parametergleichungen der beiden Geraden, die die Tauchbahnen der Roboter modellieren.

(4 BE)

2.2

Ermittle den Schnittpunkt $T$ der beiden Geraden aus Aufgabenteil 2.1.

$\bigg[$ zur Kontrolle: $T(12\mid -1\mid -7)\bigg]$

(4 BE)

2.3

Die beiden Roboter starten gleichzeitig vom Punkt $P_1$ bzw. $Q_1$ zum Zeitpunkt $t_1$ und bewegen sich auf ihren Tauchbahnen zum Schnittpunkt $T.$

Begründe, dass der Schnittpunkt $T$ auf dem Weg des Roboters $R1$ nicht zwischen $P_1$ und $P_2$ liegt, und ermittle die Koordinaten des Punktes $U,$ an dem sich $R1$ befindet, wenn der Tauchroboter $R2$ am Schnittpunkt $T$ angelangt ist.

(4 BE)

2.4

Berechne den Winkel $\alpha$ zwischen den beiden Vektoren $\overrightarrow{n}=\pmatrix{0\\0\\-1}$ und $\overrightarrow{P_1P_2}.$
Deute den Winkel $\beta=90^{\circ}-\alpha$ im Sachzusammenhang.

(4 BE)

Bei den folgenden Aufgaben werden die Tauchroboter als punktförmig angesehen.

2.5

Bei einem zweiten Tauchgang kann man ab einem bestimmten Zeitpunkt die Tauchbahnen der beiden Tauchroboter $R1$ und $R2$ folgendermaßen beschreiben:

$R1:\overrightarrow{x}=\pmatrix{15\\-22\\-2}+t\cdot \pmatrix{-7\\11\\-3}$ und $R2:\overrightarrow{x}=\pmatrix{27\\-6\\-6}+t\cdot \pmatrix{-10\\7\\-2}$

Dabei ist $t\geq 0$ die Zeit in Minuten ab diesem Zeitpunkt.

Die Vektorgleichung $\pmatrix{15\\-22\\-2}+t\cdot \pmatrix{-7\\11\\-3}=$ $\pmatrix{27\\-6\\-6}+t\cdot \pmatrix{-10\\7\\-2}$ besitzt die Lösung $t=4.$

Deute diese Lösung im Sachzusammenhang.

(3 BE)

Im Reschensee befindet sich ein feinmaschiges ebenes Netz. Das Netz verläuft durch die Punkte $N_1(-19\mid -5\mid -5,5)$ , $N_2(-23\mid -7\mid -1,5)$ und $N_3(-16\mid -3\mid -5,5).$

3.1

Gib eine Parametergleichung der Ebene $N$ an, in der das Netz liegt, und bestimme eine Koordinatengleichung dieser Ebene $N.$

$\bigg[$ eine mögliche Koordinatengleichung von $N$ lautet: $8x-12y+2z=-103\bigg]$

(6 BE)

3.2

Ein weiterer Tauchroboter $R3$ ist mit Sensoren ausgestattet, die bei einer Abstandsunterschreitung von 2 Metern zu einem Hindernis Alarm auslösen. Der Roboter $R3$ befindet sich im Punkt $P_3(-9\mid 6\mid -6)$ in der Nähe des Netzes.

Zeige, dass die Sensoren an diesem Punkt keinen Alarm auslösen.

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Aus $36 \,\text{m}^2$ Grundfläche des Quaders ergibt sich die Grundseitenlänge $g = \sqrt{36\,\text{m}^2} = 6 \,\text{m}.$

Da die Grundfläche $7\,\text{m}$ unter der Wasseroberfläche liegt, folgen die Koordinaten der Punkte im Koordinatensystem mit:

$A = (0 \mid 0 \mid-7)$

$G = (6\mid6\mid15)$

$B = (6\mid0\mid-7)$

$H = (0\mid6\mid15)$

$S = (3\mid3\mid24)$

1.2

Die Dachfläche besteht aus vier gleich großen Dreiecken.

Die Grundseite ist hierbei $6$ Meter lang.

Mit dem Satz des Pythagoras lässt sich nun die Höhe $h$ eines solchen Dreiecks ermitteln:

$\begin{array}[t]{rll} h&=&\sqrt{3^2 + 9^2} & \\[5pt] &=& \sqrt{9+81}& \\[5pt] &=& \sqrt{90} \end{array}$

Für den Flächeninhalt der vier Dreiecke folgt:

$\begin{array}[t]{rll} F &=& 4 \cdot \left(\dfrac{1}{2} \cdot g \cdot h \right)&\\[5pt] &=& 4 \cdot \dfrac{1}{2} \cdot 6 \cdot \sqrt{90} &\\[5pt] &=& 12 \cdot \sqrt{90} \end{array}$

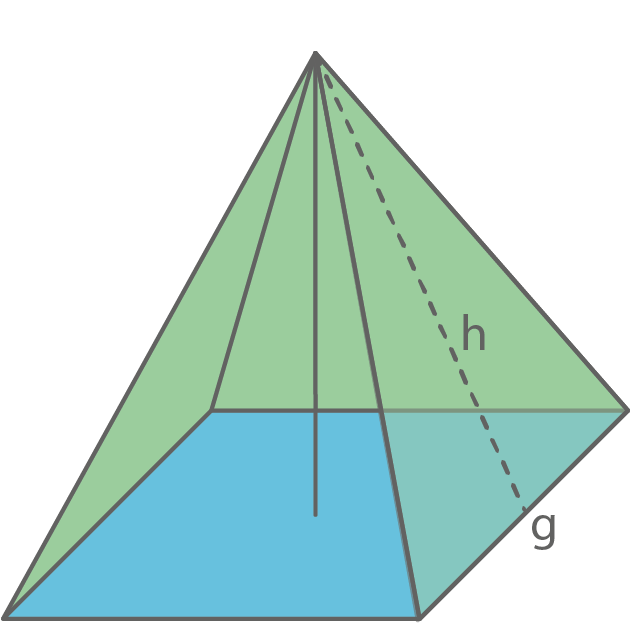
Damit beträgt der Flächeninhalt der Dachfläche $12 \cdot \sqrt{90} \,\text{m}^2.$

2.1

Parametergleichung des ersten Tauchroboters:

$\begin{array}[t]{rll} g_{1}: \overrightarrow{x}&=& P_{1} + t \cdot \overrightarrow{P_{1}P_{2}} & \\[5pt] &=&\pmatrix{24\\8\\-1} + t \cdot \pmatrix{-4\\-3\\-2} \end{array}$

Parametergleichung des zweiten Tauchroboters:

$\begin{array}[t]{rll} g_{2}: \overrightarrow{x}&=& Q_{1} + s \cdot \overrightarrow{Q_{1}Q_{2}} & \\[5pt] &=& \pmatrix{15\\0\\-5,5} + s \cdot \pmatrix{-6\\-2\\-3} \end{array}$

2.2

Gleichsetzen von $g_{1}$ und $g_{2}$ liefert:

$\pmatrix{24\\8\\-1} + t \cdot \pmatrix{-4\\-3\\-2}$ $= \pmatrix{15\\0\\-5,5} + s \cdot \pmatrix{-6\\-2\\-3}$

Auflösen der 1. Zeile nach $t$ ergibt:

$\begin{array}[t]{rll} 24 - 4t&= 15 - 6s& \quad \scriptsize \,\big \vert \, -24 \\[5pt] -4t&= -9 - 6s& \quad \scriptsize \,\big \vert \, :(-4) \\[5pt] t &= \dfrac{9}{4} + \dfrac{3}{2}s \end{array}$

Durch Einsetzen von $t$ in die 2. Zeile folgt:

$\begin{array}[t]{rll} 8 - 3t&=& -2s & \\[5pt] 8 - 3\cdot \left(\dfrac{9}{4} + \dfrac{3}{2}s\right)&=& -2s & \\[5pt] 8 - \dfrac{27}{4} - \dfrac{9}{2}s&=& -2s&\quad \scriptsize \mid\;+\dfrac{9}{2}s \\[5pt] \dfrac{5}{4} &=&\dfrac{5}{2}s &\quad \scriptsize \mid\; \cdot \ \dfrac{2}{5}\\[5pt] \dfrac{1}{2} &=& s \end{array}$

Damit ergibt sich für $t$ :

$\begin{array}[t]{rll} t&=& \dfrac{9}{4} + \dfrac{3}{2}s& \\[5pt] &=& \dfrac{9}{4} + \dfrac{3}{2}\cdot \dfrac{1}{2}& \\[5pt] &=& 3 \end{array}$

Kontrolle durch Einsetzen von $t$ und $s$ in die 3. Zeile:

$\begin{array}[t]{rll} -1 - 2t&=& -5,5 - 3s&\\[5pt] -1 -2\cdot 3&=& -5,5 - 3\cdot \dfrac{1}{2}&\\[5pt] -7&=& -7 \end{array}$

Somit existiert ein Schnittpunkt der beiden Geraden.

Um die genauen Koordinaten des Schnittpunkts $P$ zu berechnen, wird $t$ in $g_{1}$ einsetzt:

$\begin{array}[t]{rll} \overrightarrow{OP}&=& \pmatrix{24\\8\\-1} + 3 \cdot \pmatrix{-4\\-3\\-2}&\\[5pt] &=& \pmatrix{12\\-1\\-7}&\\[5pt] \end{array}$

Die Koordinaten des Schnittpunkts der beiden Geraden sind somit gegeben durch $P(12 \mid -1 \mid -7).$

2.3

Würde der Schnittpunkt $T$ auf dem Weg des Roboters $R_{1}$ zwischen $P_{1}$ und $P_{2}$ liegen, müsste folgendes gelten:

$\pmatrix{24\\8\\-1} + t \cdot \pmatrix{-4\\-3\\-2} = \pmatrix{12\\-1\\-7} \;$ für ein $\; 0 \leq t \leq 1$

Laut Aufgabenteil 2.2 gilt diese Gleichung jedoch für $t=3$ .

Somit liegt der Schnittpunkt $T$ nicht auf dem Weg des Roboters $R_{1}$ zwischen $P_{1}$ und $P_{2}$ .

Roboter $R_{2}$ erreicht Schnittpunkt $T$ zum Zeitpunkt $s = \dfrac{1}{2}$ . Um also die Koordinaten des Punktes $U$ zu ermitteln, wird $s = \dfrac{1}{2}$ für $t$ in $g_{1}$ eingesetzt:

$\begin{array}[t]{rll} \overrightarrow{ OU}&=&\pmatrix{24\\8\\-1} + \dfrac{1}{2} \cdot \pmatrix{-4\\-3\\-2} & \\[5pt] &=& \pmatrix{22\\6,5\\-2} \end{array}$

Wenn Roboter $R_{2}$ den Schnittpunkt $T$ erreicht, befindet sich Roboter $R_{1}$ somit am Punkt $U (22 \mid 6,5 \mid -2).$

2.4

Es gilt:

Rechnung anzeigen

$\alpha \approx 68,2^{\circ}$

Im Sachzusammenhang entspricht der Winkel $\beta = 90^{\circ} - \alpha \approx 21,801^{\circ}$ der Steigung, mit der sich der Roboter $R_{1}$ bezüglich der Wasseroberfläche bewegt.

2.5

Die Lösung bedeutet, dass sich die Bahnen der beiden Tauchroboter kreuzen und sich beide Tauchroboter zum gleichen Zeitpunkt $t= 4$ in ihrem Schnittpunkt treffen.

3.1

Parametergleichung aufstellen

N: \overrightarrow{x}= \overrightarrow{ON_1}+t\cdot \overrightarrow{N_1N_2}+s\cdot \overrightarrow{N_1N_3}

Parametergleichung anzeigen

Ebenengleichung bestimmen

Ein Normalenvektor der Ebene lässt sich wie folgt berechnen:

$\begin{array}[t]{rll} \overrightarrow{n}&=& \pmatrix{-4\\-2\\4} \times \pmatrix{3\\2\\0} &\\[5pt] &=& \pmatrix{(-2)\cdot 0-4\cdot 2\\4\cdot 3-(-4)\cdot 0\\(-4)\cdot 2-(-2)\cdot 3}&\\[5pt] &=& \pmatrix{-8 \\ 12 \\ -2} \end{array}$

Dadurch ergibt sich folgende Koordinatengleichung:

$N: -8 \cdot x + 12 \cdot y - 2 \cdot z = c$

Durch Einsetzen von beispielsweise $\overrightarrow{ON_1}=\pmatrix{-19\\-5\\-5,5}$ in $N$ kann $c$ berechnet werden:

$\begin{array}[t]{rll} c&=& -8 \cdot (-19) + 12 \cdot (-5) - 2 \cdot (-5,5)& \\[5pt] &=& 103 \end{array}$

Damit lautet eine mögliche Koordinatengleichung der Ebene $N: -8x + 12y -2z = 103$ beziehungsweise $N: 8x - 12y +2z = -103.$

3.2

Mit der Hesseschen Normalform lässt sich der Abstand des Roboters $R_{3}$ zum Netz $N$ berechnen:

$d(P_{3}, N)\approx 3,64$

Rechenweg anzeigen

Somit beträgt die Entfernung des Roboters zum Netz mehr als $2 \,\text{m}$ .

Folglich lösen die Sensoren keinen Alarm aus.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?