B2 - Analytische Geometrie

Mit einem GPS-Empfänger kann man seine Position auf der Erde metergenau bestimmen. Dies geschieht mit Hilfe von Satelliten, die ihre Signale in alle Richtungen zur Erde senden. Je mehr Satelliten empfangen werden können, desto sicherer und genauer wird die Positionsbestimmung. Nimm an, dass sich der Satellit NAVSTAR momentan auf der Position $N(0\mid10\mid20203)$ und der Satellit KOSMOS auf $K(4309\mid2801\mid20513)$ befindet (alle Angaben in km). Ein GPS-Empfänger auf der Erde empfängt die Signale beider Satelliten. Das Signal von NAVSTAR wird aus Richtung des Vektors $\overrightarrow{v}=\begin{pmatrix}25\\ 37\\ -1010\end{pmatrix}$ empfangen und das von KOSMOS aus Richtung des Vektors $\overrightarrow{w}=\begin{pmatrix}-13\\ -7\\ -70\end{pmatrix}.$

1.1

Gib eine Gleichung der Geraden an, die von $K$ aus in Richtung des Vektors $\overrightarrow{w}$ verläuft, und beschreibe den Aufbau dieser Gleichung.

(3 BE)

1.2

Zeige, dass sich der GPS-Empfänger auf der Position $E(500\mid750\mid3)$ befindet.

(4 BE)

1.3

Berechne den Abstand des Satelliten KOSMOS zum Empfänger.

(3 BE)

1.4

Berechne, in welchem Winkel zueinander die Signale beim Empfänger eintreffen.

(3 BE)

Geocaches sind in der Natur versteckte „Schätze“, die man mittels GPS-Koordinaten finden kann. Man kann sich diese immer beliebter werdende Freizeitbeschäftigung als eine Art elektronische Schatzsuche vorstellen. Die GPS-Koordinaten zu einem Geocache findet man im Internet.
Ein Schatzsucher steht in $A(2\mid0\mid0)$ direkt am Fuße einer steil ansteigenden, mit einigen Bäumen bewachsenen Ebene. In der Nähe der Ebene befindet sich ein Geocache in $G(3,1\mid6\mid1,4)$ . Von seiner Position in $A$ aus peilt der Schatzsucher zunächst die beiden in der Ebene liegenden, markanten Punkte $B(1\mid3\mid1)$ und $C(-5\mid6\mid3)$ an. (1 LE $\mathrel{\widehat{=}}100\;\text{m}$ )

2.1

Bestimme eine Parametergleichung und eine Koordinatengleichung der Ebene $E_1$ , die durch die Punkte $A$ , $B$ und $C$ verläuft.
$[\text{zur Kontrolle: } E_1: 3x - 4y + 15z = 6]$

(5 BE)

2.2

Erläutere die folgenden vier Rechenschritte und die Bedeutung der Rechnung im Sachzusammenhang:

$E_1:3x-4y+15z=6$ $\Rightarrow \overrightarrow{n_1}=\begin{pmatrix}3\\-4\\15\end{pmatrix}$

$E_2:z=0 \Rightarrow \overrightarrow{n_2}=\begin{pmatrix}0\\ 0\\ 1\end{pmatrix}$

$\cos(\gamma)=\dfrac{\mid \overrightarrow{n_1}\cdot \overrightarrow{n_2} \mid}{\mid \overrightarrow{n_1}\mid \cdot \mid\overrightarrow{n_2} \mid}$ $=\dfrac{15}{\sqrt{250}}\Rightarrow \gamma \approx18,4^{\circ}$

$\tan(\gamma)\approx 33,3 \;\%$

(6 BE)

2.3

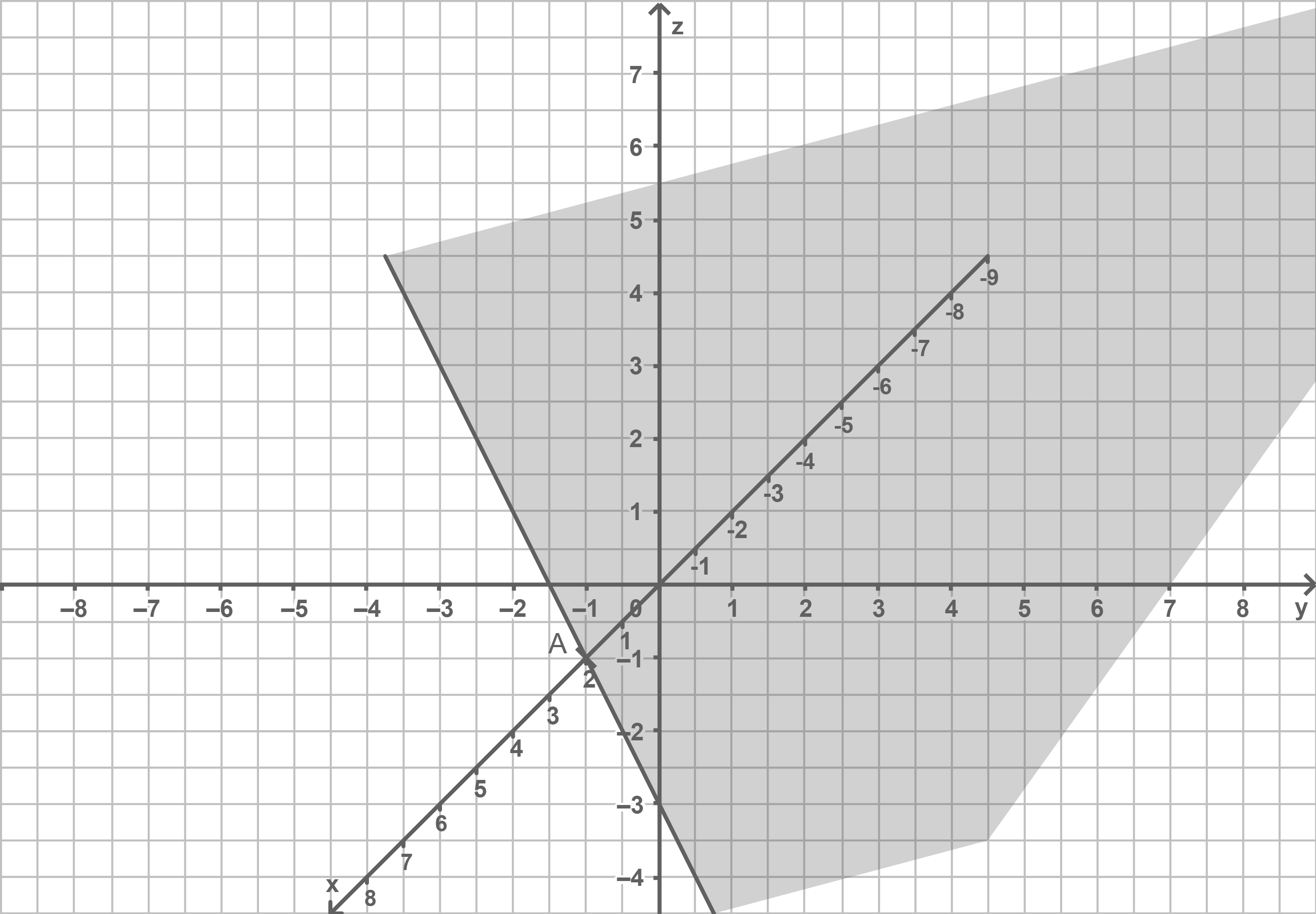
Zeichne die Lage des Geocaches in $G(3,1\mid6\mid1,4)$ als Punkt im Material ein. Untersuche rechnerisch, ob der Geocache über, auf oder unter der Erdoberfläche versteckt ist.

(6 BE)

Material

1.1

Geradengleichung angeben

Mit dem Ortsvektor von $K$ als Stützvektor und $\overrightarrow{w}$ als Richtungsvektor folgt als Geradengleichung:

$g: \overrightarrow{x}$ $=\overrightarrow{OK}$ $+ s \cdot \overrightarrow{w}$ $= \begin{pmatrix}4309\\2801\\20513\end{pmatrix}$ $+ s \cdot \begin{pmatrix}-13\\-7\\-70\end{pmatrix}$

Aufbau beschreiben

$x$ ist der Ortsvektor eines beliebigen Punktes der Geraden $g$ .
$\overrightarrow{w}$ ist der Richtungsvektor der Geraden $g$ , d.h. die Gerade verläuft wie gefordert in Richtung dieses Vektors.
$\overrightarrow{OK}$ ist der Stützvektor der Geraden $g.$ Damit liegt der Punkt $K$ auf der Geraden $g$ .
$s$ ist eine Variable die alle reelen Zahlen annehmen kann und somit den Richtungsvektor beliebig strecken und stauchen kann.

1.2

Das zweite Signal kann durch die Gerade $h,$ die vom Punkt $N$ aus in Richtung $\overrightarrow{v}$ verläuft, beschrieben werden. Da der GPS-Empfänger auf beiden Geraden liegt, reicht es eine Punktprobe durchzuführen und zu zeigen, dass die Geraden $g$ und $h$ verschieden sind.

1. Schritt: Geradengleichung von $h$ aufstellen

Mit $\overrightarrow{ON}$ als Stützvektor und $\overrightarrow{v}$ als Richtungsvektor folgt:

$h: \overrightarrow{x}$ $= \overrightarrow{ON}$ $+ t \cdot \overrightarrow{v}$ $= \begin{pmatrix}0\\10\\20203\end{pmatrix}$ $+ t \cdot \begin{pmatrix}25\\37\\-1010\end{pmatrix}$

2. Schritt: Punktproben durchführen

Die Punktprobe von $E$ bezüglich $g$ liefert:

Rechenweg anzeigen

$s = 293$

Der Punkt $E$ liegt auf der Geraden $g,$ da für $s=293$ alle drei Gleichungen erfüllt sind.

Für die Punktprobe bezüglich $h$ folgt:

Rechenweg anzeigen

$t = 20$

Für $t=20$ sind alle drei Gleichungen erfüllt und der Punkt $E$ liegt damit auch auf der Geraden $h.$

3. Schritt: Lineare Unabhängigkeit zeigen

Wenn die beiden Richtungsvektoren linear abhängig wären, existiert ein $u$ mit dem folgt:

$\begin{pmatrix}-13\\-7\\-70\end{pmatrix}$ $= u \cdot \begin{pmatrix}25\\37\\-1010\end{pmatrix}$

Das gesuchte $u$ müsste aufgrund der Gleichung der ersten beiden Komponenten negativ sein, wegen der Gleichung der dritten Komponente aber positiv. Somit kann es kein solches $u$ geben und die Richtungsvektoren sind linear unabhängig, das heißt die Geraden $g$ und $h$ sind verschieden. Damit liegt der GPS-Empfänger im Punkt $E.$

1.3

Rechenweg anzeigen

$| \overrightarrow{EK} | \approx 20961$

Der gesuchte Abstand beträgt damit ca. $20961 \text{ km}.$

1.4

Rechenweg anzeigen

$\alpha \approx 14,2^{\circ}$

Der Winkel zwischen den Richtungsvektoren, und damit auch der Winkel zwischen den beiden Geraden in dem Punkt in dem die Signale aufeinandertreffen, beträgt ca. $14,2^{\circ}.$

2.1

Parametergleichung bestimmen

Da die Punkte $A, B$ und $C$ in der Ebene liegen, folgt mit $\overrightarrow{OA}$ als Stützvektor und $\overrightarrow{AB}$ und $\overrightarrow{AC}$ eine Parameterform der Ebene. Die Berechnung der Spannvektoren liefert:

$\overrightarrow{AB}$ $=\overrightarrow{OB}$ $-\overrightarrow{OA}$ $= \begin{pmatrix}1\\3\\1\end{pmatrix}$ $-\begin{pmatrix}2\\0\\0\end{pmatrix}$ $=\begin{pmatrix}-1\\3\\1\end{pmatrix},$

$\overrightarrow{AC}$ $=\overrightarrow{OC}$ $-\overrightarrow{OA}$ $= \begin{pmatrix}-5\\6\\3\end{pmatrix}$ $-\begin{pmatrix}2\\0\\0\end{pmatrix}$ $=\begin{pmatrix}-7\\6\\3\end{pmatrix}.$

Einsetzen in die Parameterform liefert:

$E_1: \overrightarrow{x}$ $=\overrightarrow{OA}$ $+ t \cdot \overrightarrow{AB}$ $+ s \cdot \overrightarrow{AC}$ $= \begin{pmatrix}2\\0\\0\end{pmatrix}$ $+ t \cdot \begin{pmatrix}-1\\3\\1\end{pmatrix}$ $+ s \cdot \begin{pmatrix}-7\\6\\3\end{pmatrix}.$

Koordinatengleichung bestimmen

Mit Hilfe des crossP-Befehls des CAS folgt für den Normalenvektor $\overrightarrow{n}$ der Ebene:

$\overrightarrow{n}$ $= \begin{pmatrix}-1\\3\\1\end{pmatrix}$ $\times \begin{pmatrix}-7\\6\\3\end{pmatrix}$ $= \begin{pmatrix} 3\\-4\\15 \end{pmatrix}$

Mathematische Darstellung eines Vektorprodukts in einer Softwareanwendung.

Einsetzen von $P(2 \mid 0 \mid 0)$ in die Ebenengleichung liefert dann:

$E_1: n_1\cdot p_1$ $+ n_2\cdot p_2$ $+ n_3\cdot p_3$ $= 3\cdot 2$ $+ (-4)\cdot 0$ $+ 15\cdot 0$ $= 6.$

Einsetzen in die allgemeine Koordinatenform liefert das Ergebnis:

$E_1: 3\cdot x$ $- 4\cdot y$ $+ 15 \cdot z$ $=6.$

2.2

Rechenschritte erläutern

Im ersten Schritt wird der Normalenvektor der Ebene $E_1$ abgelesen, das hießt im Sachzusammenhang der Normalenvektor der steil ansteigenden mit Bäumen bewachsenen Ebene.
Im zweiten Schritt wird nun der Normalenvektor der $x$ - $y$ -Ebene $E_2$ abgelesen, welche im Sachzusammenhang die Erdoberfläche darstellt.
Der dritte Schritt führt die Berechnung des Schnittwinkels der beiden Ebenen mit Hilfe derer Normalenvektoren durch. Im Sachzusammenhang wird hier überprüft, unter welchem Winkel die mit Bäumen bewachsene Ebene gegenüber der Erdoberfläche ansteigt.
Im letzten Schritt wird der Tangens des Schnittwinkels berechnet, das heißt die prozentuale Steigung der mit Bäumen bewachsenen Ebene. Diese hat also eine Steigung von $33\; \%$ gegenüber der Erdoberfläche.

2.3

Geocache einzeichnen

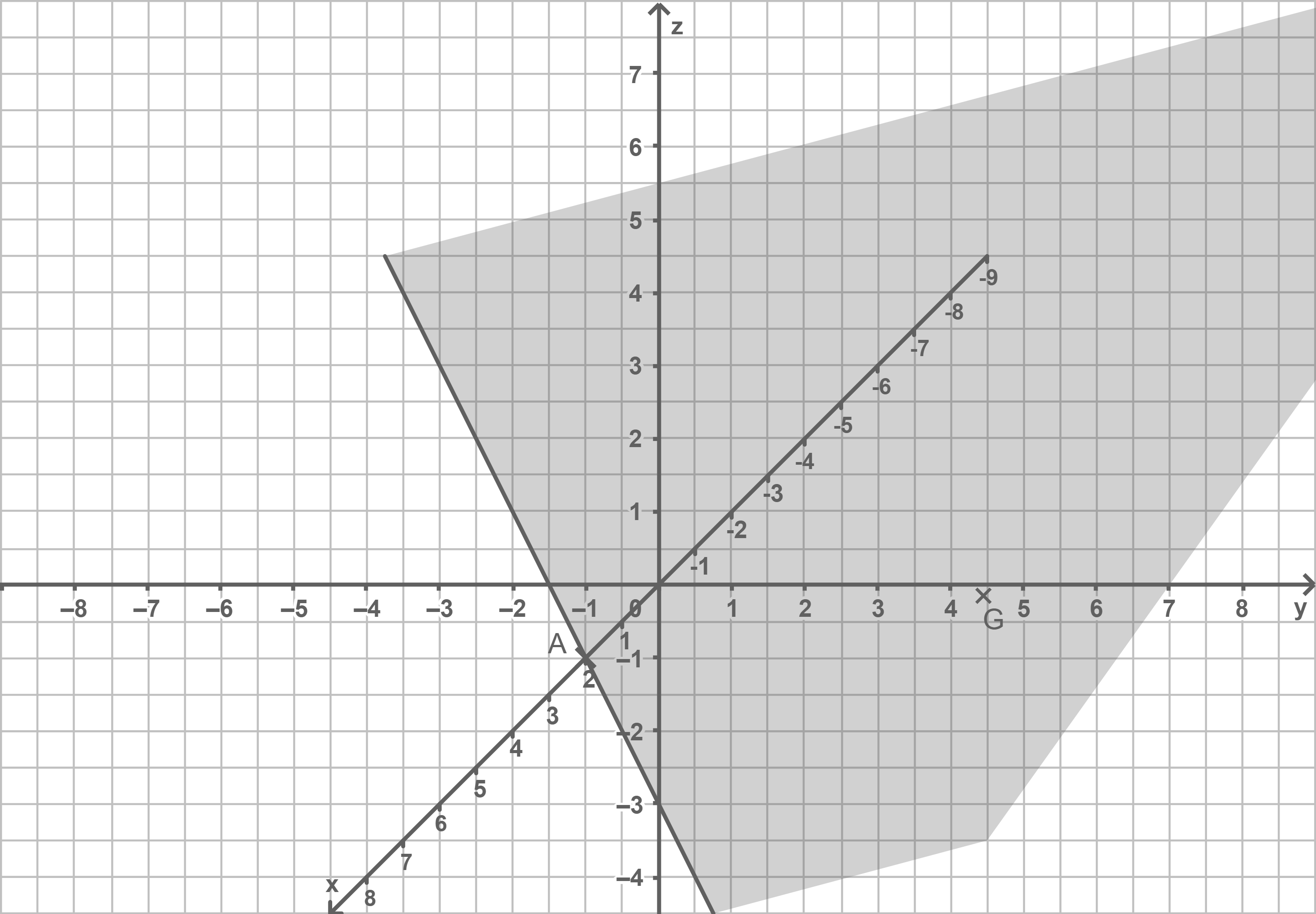Die Lage des Geocaches im Punkt $G$ kann mit Hilfe der Lotgeraden $h$ zur $x$ - $y$ -Ebene bestimmt werden.

1. Schritt: Lotgerade $h$ aufstellen

Da die Lotgerade $h$ zur $x$ - $y$ -Ebene durch $G$ orthogonal zur $x$ - $y$ -Ebene ist, folgt:

$h:\overrightarrow{x}$ $= \pmatrix{3,1\\6\\1,4}$ $+ r \cdot \pmatrix{0\\0\\1}.$

2. Schritt: Schnittpunkt von $h$ und $E_1$ bestimmen

Einsetzen eines allgemeinen Punktes $S(3,1 \mid 6 \mid 1,4 + r)$ der Geraden $h$ in die Koordinatengleichung $E_1:\;3x$ $-4y$ $+15z$ $=6$ und Auflösen nach $r$ liefert:

Rechenweg anzeigen

$r = -0,02$

Der Schnittpunkt hat somit die Koordinaten $S(3,1 \mid 6 \mid 1,38).$ Da $r=-0,02$ negativ ist, liegt der Punkt $G,$ und damit das Geocache, oberhalb der Ebene $E_1,$ also über der Erdoberfläche.

1.1

Geradengleichung angeben

Mit dem Ortsvektor von $K$ als Stützvektor und $\overrightarrow{w}$ als Richtungsvektor folgt als Geradengleichung:

$g: \overrightarrow{x}$ $=\overrightarrow{OK}$ $+ s \cdot \overrightarrow{w}$ $= \begin{pmatrix}4309\\2801\\20513\end{pmatrix}$ $+ s \cdot \begin{pmatrix}-13\\-7\\-70\end{pmatrix}$

Aufbau beschreiben

$x$ ist der Ortsvektor eines beliebigen Punktes der Geraden $g$ .
$\overrightarrow{w}$ ist der Richtungsvektor der Geraden $g$ , d.h. die Gerade verläuft wie gefordert in Richtung dieses Vektors.
$\overrightarrow{OK}$ ist der Stützvektor der Geraden $g.$ Damit liegt der Punkt $K$ auf der Geraden $g$ .
$s$ ist eine Variable die alle reelen Zahlen annehmen kann und somit den Richtungsvektor beliebig strecken und stauchen kann.

1.2

1. Schritt: Geradengleichung von $h$ aufstellen

Mit $\overrightarrow{ON}$ als Stützvektor und $\overrightarrow{v}$ als Richtungsvektor folgt:

$h: \overrightarrow{x}$ $= \overrightarrow{ON}$ $+ t \cdot \overrightarrow{v}$ $= \begin{pmatrix}0\\10\\20203\end{pmatrix}$ $+ t \cdot \begin{pmatrix}25\\37\\-1010\end{pmatrix}$

2. Schritt: Punktproben durchführen

Die Punktprobe von $E$ bezüglich $g$ liefert:

Rechenweg anzeigen

$s = 293$

Der Punkt $E$ liegt auf der Geraden $g,$ da für $s=293$ alle drei Gleichungen erfüllt sind.

Für die Punktprobe bezüglich $h$ folgt:

Rechenweg anzeigen

$t = 20$

Für $t=20$ sind alle drei Gleichungen erfüllt und der Punkt $E$ liegt damit auch auf der Geraden $h.$

3. Schritt: Lineare Unabhängigkeit zeigen

Wenn die beiden Richtungsvektoren linear abhängig wären, existiert ein $u$ mit dem folgt:

$\begin{pmatrix}-13\\-7\\-70\end{pmatrix}$ $= u \cdot \begin{pmatrix}25\\37\\-1010\end{pmatrix}$

1.3

Rechenweg anzeigen

$| \overrightarrow{EK} | \approx 20961$

Der gesuchte Abstand beträgt damit ca. $20961 \text{ km}.$

1.4

Mit Hilfe des CAS unter Interactive $\to$ Vector $\to$ angle folgt für den Winkel $\alpha$ zwischen den Richtungsvektoren:

$\alpha \approx 14,2^{\circ}$

Mathematische Berechnung mit Matrizen und Winkelfunktion in einer Software-Oberfläche.

Der Winkel zwischen den Richtungsvektoren, und damit auch der Winkel zwischen den beiden Geraden in dem Punkt in dem die Signale aufeinandertreffen, beträgt ca. $14,2^{\circ}.$

2.1

Parametergleichung bestimmen

$\overrightarrow{AB}$ $=\overrightarrow{OB}$ $-\overrightarrow{OA}$ $= \begin{pmatrix}1\\3\\1\end{pmatrix}$ $-\begin{pmatrix}2\\0\\0\end{pmatrix}$ $=\begin{pmatrix}-1\\3\\1\end{pmatrix},$

$\overrightarrow{AC}$ $=\overrightarrow{OC}$ $-\overrightarrow{OA}$ $= \begin{pmatrix}-5\\6\\3\end{pmatrix}$ $-\begin{pmatrix}2\\0\\0\end{pmatrix}$ $=\begin{pmatrix}-7\\6\\3\end{pmatrix}.$

Einsetzen in die Parameterform liefert:

Koordinatengleichung bestimmen

Mit Hilfe des crossP-Befehls des CAS folgt für den Normalenvektor $\overrightarrow{n}$ der Ebene:

$\overrightarrow{n}$ $= \begin{pmatrix}-1\\3\\1\end{pmatrix}$ $\times \begin{pmatrix}-7\\6\\3\end{pmatrix}$ $= \begin{pmatrix} 3\\-4\\15 \end{pmatrix}$

Einsetzen von $P(2 \mid 0 \mid 0)$ in die Ebenengleichung liefert dann:

$E_1: n_1\cdot p_1$ $+ n_2\cdot p_2$ $+ n_3\cdot p_3$ $= 3\cdot 2$ $+ (-4)\cdot 0$ $+ 15\cdot 0$ $= 6.$

Einsetzen in die allgemeine Koordinatenform liefert das Ergebnis:

$E_1: 3\cdot x$ $- 4\cdot y$ $+ 15 \cdot z$ $=6.$

2.2

Rechenschritte erläutern

2.3

Geocache einzeichnen

Die Lage des Geocaches im Punkt $G$ kann mit Hilfe der Lotgeraden $h$ zur $x$ - $y$ -Ebene bestimmt werden.

1. Schritt: Lotgerade $h$ aufstellen

Da die Lotgerade $h$ zur $x$ - $y$ -Ebene durch $G$ orthogonal zur $x$ - $y$ -Ebene ist, folgt:

$h:\overrightarrow{x}$ $= \pmatrix{3,1\\6\\1,4}$ $+ r \cdot \pmatrix{0\\0\\1}.$

2. Schritt: Schnittpunkt von $h$ und $E_1$ bestimmen

Einsetzen eines allgemeinen Punktes $S(3,1 \mid 6 \mid 1,4 + r)$ der Geraden $h$ in die Koordinatengleichung $E_1:\;3x$ $-4y$ $+15z$ $=6$ und Auflösen nach $r$ liefert:

Rechenweg anzeigen

$r = -0,02$

Der Schnittpunkt hat somit die Koordinaten $S(3,1 \mid 6 \mid 1,38).$ Da $r=-0,02$ negativ ist, liegt der Punkt $G,$ und damit das Geocache, oberhalb der Ebene $E_1,$ also über der Erdoberfläche.