B2 - Analytische Geometrie

In Rom am Piazzale Ostiense steht nach ägyptischem Vorbild die $40\,\text{m}$ hohe Cestius-Pyramide. Die Seitenlängen der quadratischen Grundfläche $ABCD$ betragen $30\,\text{m}$ . Die Spitze der Pyramide liegt in $S\ (15\mid 15\mid40)$ (alle Angaben in Metern).

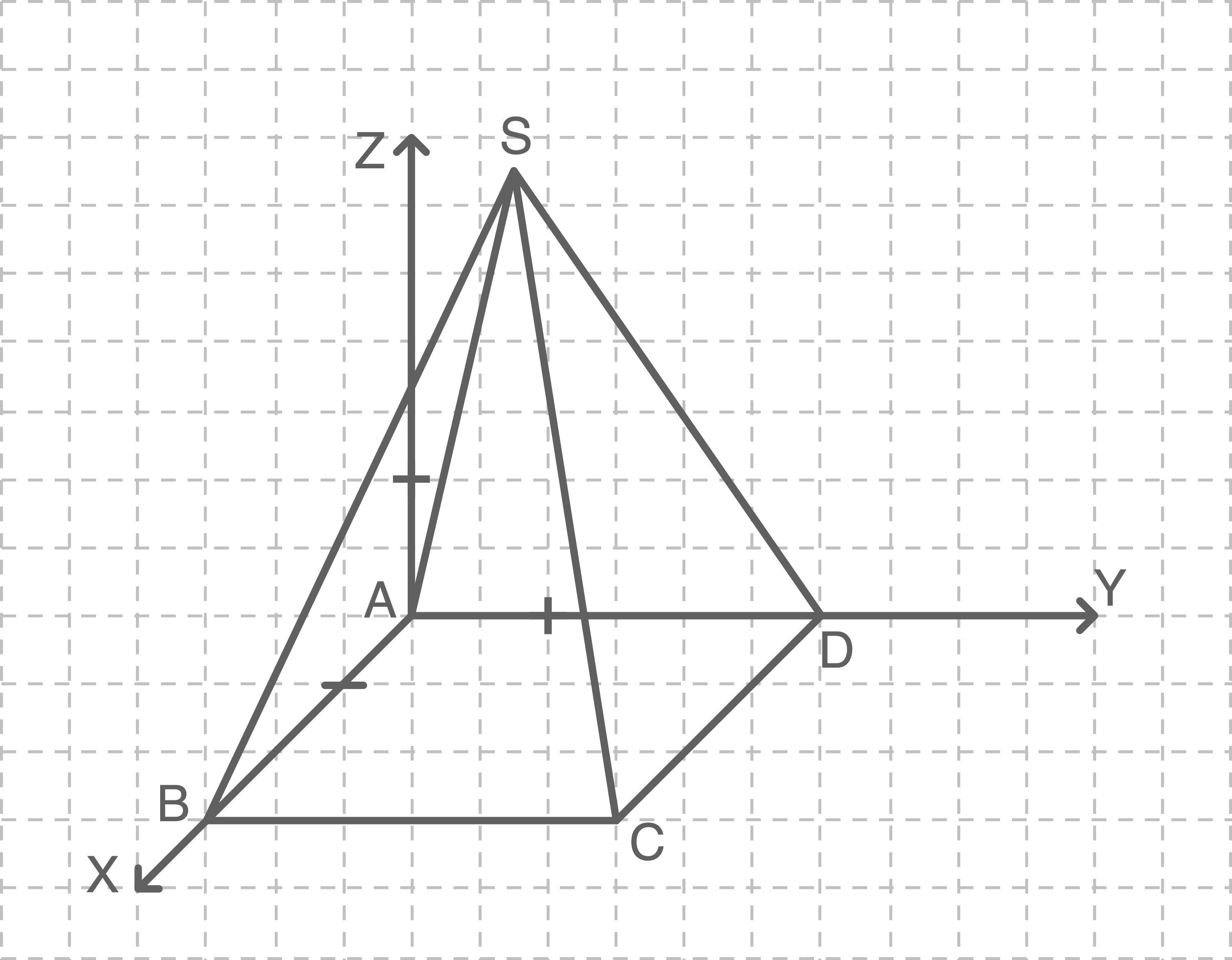
Cestius-Pyramide

Gib die Skalierung der Achsen des Koordinatensystems aus der Aufgabenstellung und die Koordinaten der Eckpunkte $A$ , $B$ , $C$ und $D$ an.

(5 BE)

Ermittle eine Parametergleichung und eine Koordinatengleichung der Ebene $E$ , in der die Pyramidenfläche $CDS$ liegt.

$[$ zur Kontrolle: $8y+3z=240$ ist eine mögliche Koordinatengleichung von $E.]$

(5 BE)

Zur Säuberung der teilweise mit Moos und Unkraut bewachsenen Pyramide muss ein Gebäudereiniger an den Seitenflächen hochsteigen. Bei Gebäudeflächen mit einer Neigung von mehr als $60^{\circ}$ darf er diese nur mit Sicherung besteigen.

Entscheide durch eine geeignete Rechnung, ob hier eine solche Sicherung notwendig ist.

(4 BE)

Die Strahlen der Vormittagssonne fallen zu einem bestimmten Zeitpunkt in Richtung des Vektors $\vec{s_v}=\begin{pmatrix}1\\2\\-4 \end{pmatrix}$ auf die Pyramide. Eine Touristin sitzt zu diesem Zeitpunkt gegenüber der Pyramide in einem Café. Eines ihrer Augen befindet sich im Punkt $T\,(24,75\mid 34,5\mid 1)$ .

Bestätige durch eine geeignete Rechnung, dass der Schatten der Pyramidenspitze genau in dieses Auge fällt.

(4 BE)

Um die Mittagszeit fallen die Sonnenstrahlen nun in Richtung des Vektors $\vec{s_M}=\begin{pmatrix}2\\1\\-20 \end{pmatrix}$ auf die Cestius-Pyramide. Zeige rechnerisch, dass zu diesem Zeitpunkt die Pyramide keinen Schatten spenden kann.

(6 BE)

Zur Überprüfung der Stabilität des Gesteins der Pyramide wird eine Probebohrung angeordnet. Dazu wird senkrecht zur Seitenfläche $CDS$ eine Bohrung bis zum Mittelpunkt der quadratischen Grundfläche durchgeführt. Berechne die Koordinaten des Punktes $P$ auf der Seitenfläche $CDS$ , in dem die Bohrung beginnen muss.

Bestimme die Länge des entstehenden Bohrkanals.

$[$ zur Kontrolle: Auf zwei Nachkommastellen gerundet ergibt sich $P\ (\ 15\ |\ 28,15\ |\ 4,93).]$

(6 BE)

Bildnachweise [nach oben]

[1]

https://commons.wikimedia.org/wiki/File:2012-07-04_Piazzale_Ostiense.jpg - Piazzale Ostiense in Rome; on the left the Pyramid of Caius Cestius, on the right Porta San Paolo, Blackcat, CC BY-SA 3.0.