C - Stochastik
Jedes Jahr im Frühjahr gibt der DRV (Deutscher ReiseVerband e.V.) in einer Broschüre einen Kurzüberblick über die wichtigsten Daten der Tourismusbranche. Sofern nicht anders angegeben, beziehen sich die Zahlen dieser Aufgabe auf die von Deutschen durchgeführten Reisen im Jahr 2012.
1.
Für die Reiseziele der Reisen ab fünf Tagen Dauer hat der DRV folgende Zahlen ermittelt:
 % der Reiseziele lagen in Deutschland,
% der Reiseziele lagen in Deutschland,  % der Reisen waren Fernreisen. Der Rest verteilte sich auf Nah- und Mittelstreckenziele.
% der Reisen waren Fernreisen. Der Rest verteilte sich auf Nah- und Mittelstreckenziele.
Gehe im Folgenden davon aus, dass die angegebenen Zahlen auch für das Jahr 2015 gleich bleiben.
Es werden 100 von Deutschen durchgeführte Reisen ab fünf Tagen Dauer für das Jahr 2015 zufällig ausgewählt.
Gehe im Folgenden davon aus, dass die angegebenen Zahlen auch für das Jahr 2015 gleich bleiben.
Es werden 100 von Deutschen durchgeführte Reisen ab fünf Tagen Dauer für das Jahr 2015 zufällig ausgewählt.
1.1
Bestimme jeweils unter Angabe einer Zufallsgröße  die Wahrscheinlichkeiten folgender Ereignisse:
die Wahrscheinlichkeiten folgender Ereignisse:
Unter den 100 Reisen
Unter den 100 Reisen
- führen genau 31 zu einem Reiseziel innerhalb Deutschlands,
- führen mindestens 31 zu einem Reiseziel innerhalb Deutschlands,
- sind mindestens sechs, aber höchstens acht Fernreisen.
(8 BE)
1.2
Erläutere die Bedeutung der folgenden Gleichung im Sachzusammenhang.





(3 BE)
2.
Der DRV erfasst gesondert Kurzurlaube. Kurzurlaube sind Urlaube, deren Reisedauer unter fünf Tagen liegt.
 % aller Kurzurlaube gingen ins Inland.
% aller Kurzurlaube gingen ins Inland.  % aller Kurzurlaube ins Inland waren Städtereisen.
% aller Kurzurlaube ins Inland waren Städtereisen.
 % aller Kurzurlaube waren Städtereisen ins Ausland.
% aller Kurzurlaube waren Städtereisen ins Ausland.
2.1
Stelle den Sachverhalt mit Hilfe eines Baumdiagramms oder einer Vierfeldertafel dar.
(5 BE)
2.2
Es wurden insgesamt 74,5 Mio. Kurzreisen angetreten. Ermittle die Gesamtzahl der Städtereisen.
(2 BE)
2.3
Bei den Kurzurlauben geht ein Reiseanbieter davon aus, dass sich das Reiseverhalten der Deutschen in den folgenden Jahren nicht ändert. Die ermittelten Zahlen aus dem Jahr 2012 werden daher übernommen.
Dem Reiseanbieter liegt im Jahr 2015 eine Buchung einer Städtereise vor. Ermittle die Wahrscheinlichkeit, dass es sich um eine Auslandsreise handelt.
Dem Reiseanbieter liegt im Jahr 2015 eine Buchung einer Städtereise vor. Ermittle die Wahrscheinlichkeit, dass es sich um eine Auslandsreise handelt.
(3 BE)
3.
Der DRV stellt in seiner Broschüre außerdem fest, dass im Jahr 2012  % der Pauschalreisen online gebucht wurden.
% der Pauschalreisen online gebucht wurden.
Eine Reisebürokette vermutete, dass sich der Anteil der online gebuchten Pauschalreisen im Jahr 2013 erhöht habe. Um dies zu überprüfen, wurden 100 von Deutschen durchgeführte Pauschalreisen des Jahres 2013 zufällig ausgewählt und die betroffenen Reisenden nach ihrem Buchungsverhalten befragt.
Eine Reisebürokette vermutete, dass sich der Anteil der online gebuchten Pauschalreisen im Jahr 2013 erhöht habe. Um dies zu überprüfen, wurden 100 von Deutschen durchgeführte Pauschalreisen des Jahres 2013 zufällig ausgewählt und die betroffenen Reisenden nach ihrem Buchungsverhalten befragt.
3.1
Die Reisebürokette testete die Nullhypothese:

Entwickle im Sachzusammenhang eine Entscheidungsregel auf einem Signifikanzniveau von %.
%.
Entwickle im Sachzusammenhang eine Entscheidungsregel auf einem Signifikanzniveau von
(5 BE)
3.2
Solltest du in Aufgabe 3.1 zu keiner Lösung gekommen sein, so verwende als kritische Zahl, d.h. als kleinsten Wert im Ablehnungsbereich der Nullhypothese,  .
.
3.2.1
Erläutere den Fehler 1. Art und den Fehler 2. Art im Sachzusammenhang.
(2 BE)
3.2.2
Im Frühjahr 2014 gab der DRV bekannt, dass 15 % der von Deutschen im Jahr 2013 durchgeführten Pauschalreisen online gebucht wurden. Ermittle die Wahrscheinlichkeit, dass die Reisebürokette bei ihrem Hypothesentest einen Fehler 2. Art beging.
Material
Binomialsummenfunktion
(2 BE)
1.1
Wahrscheinlichkeit des ersten Ereignisses bestimmen
Die Zufallsvariable  ist binomialverteilt mit den Parametern
ist binomialverteilt mit den Parametern  und
und  und gibt die Anzahl der Reisen mit einem Reiseziel innerhalb Deutschlands an. Mit Hilfe des binomPdf-Befehl des CAS folgt:
und gibt die Anzahl der Reisen mit einem Reiseziel innerhalb Deutschlands an. Mit Hilfe des binomPdf-Befehl des CAS folgt:

_2015_c_l1b1_ti.png) Die Wahrscheinlichkeit, dass unter den
Die Wahrscheinlichkeit, dass unter den  Reisen genau
Reisen genau  ein Reiseziel innerhalb Deutschlands haben, beträgt ca.
ein Reiseziel innerhalb Deutschlands haben, beträgt ca.  Wahrscheinlichkeit des zweiten Ereignisses bestimmen
Mit Hilfe derselben Zufallsvariable
Wahrscheinlichkeit des zweiten Ereignisses bestimmen
Mit Hilfe derselben Zufallsvariable  wie beim ersten Ereignis folgt wieder mit dem binomCdf-Befehl des CAS:
wie beim ersten Ereignis folgt wieder mit dem binomCdf-Befehl des CAS:

_2015_c_l1b2_ti.png) Die Wahrscheinlichkeit, dass unter den
Die Wahrscheinlichkeit, dass unter den  Reisen mindestens
Reisen mindestens  ein Reiseziel innerhalb Deutschlands haben, beträgt ca.
ein Reiseziel innerhalb Deutschlands haben, beträgt ca.  Wahrscheinlichkeit des dritten Ereignisses bestimmen
Nun ist
Wahrscheinlichkeit des dritten Ereignisses bestimmen
Nun ist  eine binomialverteilte Zufallsgröße mit den Parametern
eine binomialverteilte Zufallsgröße mit den Parametern  und
und  die angibt, wieviele von den
die angibt, wieviele von den  betrachteten Reisen Fernreisen sind. Mit dem binomPdf-Befehl des CAS folgt:
betrachteten Reisen Fernreisen sind. Mit dem binomPdf-Befehl des CAS folgt:

_2015_c_l1b3_ti.png) Die Wahrscheinlichkeit, dass unter den
Die Wahrscheinlichkeit, dass unter den  Reisen mindestens sechs, aber höchstens acht Fernreisen sind, beträgt damit ca.
Reisen mindestens sechs, aber höchstens acht Fernreisen sind, beträgt damit ca. 
_2015_c_l1b1_ti.png)
_2015_c_l1b2_ti.png)
_2015_c_l1b3_ti.png)
1.2
Bedeutung der Gleichung erläutern
Die Gleichung gibt die Wahrscheinlichkeit dafür an, dass eine binomialverteilte Zufallsgröße  mit Parametern
mit Parametern  und
und  exakt den Wert
exakt den Wert  annimmt.
annimmt.
Da



 gilt, kann mit Hilfe der Wahrscheinlichkeiten aus der Aufgabenstellung geschlossen werden, dass
gilt, kann mit Hilfe der Wahrscheinlichkeiten aus der Aufgabenstellung geschlossen werden, dass  unter
unter  ausgewählten Reisen die Anzahl der Reisen mit Nah- und Mittelstreckenzielen angibt.
ausgewählten Reisen die Anzahl der Reisen mit Nah- und Mittelstreckenzielen angibt.
Die Gleichung besagt also im Sachzusammenhang, dass die Wahrscheinlichkeit dafür, dass unter zufällig ausgewählten Reisen genau
zufällig ausgewählten Reisen genau  Reisen Nah- oder Mittelstreckenziele haben,
Reisen Nah- oder Mittelstreckenziele haben,  beträgt.
beträgt.
Da
Die Gleichung besagt also im Sachzusammenhang, dass die Wahrscheinlichkeit dafür, dass unter
2.1
Lösungsweg A: Baumdiagramm zeichnen
Die Wahrscheinlichkeit für einen Kurzuralub im Ausland ergibt sich als Gegenereignis eines Kurzurlaubes im Inland wie folgt:





 Analog ergibt sich für Kurzurlaube im Inland, die Städtereisen sind:
Analog ergibt sich für Kurzurlaube im Inland, die Städtereisen sind:






 Da
Da  aller Kurzurlaube Städtereisen ins Ausland waren, folgt weiter:
Für Kurzurlaube ins Ausland, die keine Städtereisen waren, ergibt sich damit:
aller Kurzurlaube Städtereisen ins Ausland waren, folgt weiter:
Für Kurzurlaube ins Ausland, die keine Städtereisen waren, ergibt sich damit:






 Mit „I“ als Bezeichnung für Kurzurlaube im Inland, „S“ als Bezeichnung für Kurzurlaube, die Städtereisen sind und den Werten aus der Aufgabenstellung folgt:
Mit „I“ als Bezeichnung für Kurzurlaube im Inland, „S“ als Bezeichnung für Kurzurlaube, die Städtereisen sind und den Werten aus der Aufgabenstellung folgt:
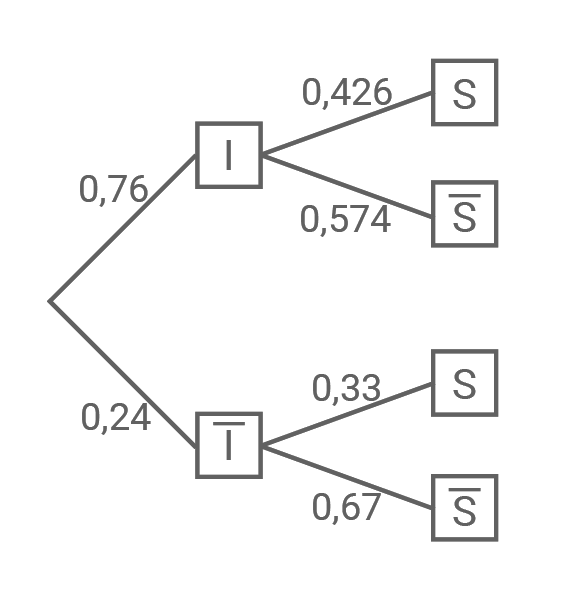 Lösungsweg B: Vierfeldertafel zeichnen
Die Wahrscheinlichkeit für eine Reise ins Ausland ergibt sich durch:
Lösungsweg B: Vierfeldertafel zeichnen
Die Wahrscheinlichkeit für eine Reise ins Ausland ergibt sich durch:





 Für die Wahrscheinlichkeit für eine Reise ins Ausland, die keine Städtereise ist, folgt:
Mit Hilfe der Wahrscheinlichkeit
Für die Wahrscheinlichkeit für eine Reise ins Ausland, die keine Städtereise ist, folgt:
Mit Hilfe der Wahrscheinlichkeit  aus der Aufgabenstellung folgt weiter:
Mit den Rechenregeln für die Vierfeldertafel und den Werten aus der Aufgabenstellung ergibt sich zudem:
Insgesamt folgt damit:
aus der Aufgabenstellung folgt weiter:
Mit den Rechenregeln für die Vierfeldertafel und den Werten aus der Aufgabenstellung ergibt sich zudem:
Insgesamt folgt damit:

| Städtereise | keine Städtereise | ||
|---|---|---|---|
| Ausland | |||
| Inland | |||
2.2
1. Schritt:  ermitteln
Lösungsweg A: Aus der Vierfeldertafel ablesen
ermitteln
Lösungsweg A: Aus der Vierfeldertafel ablesen
 Lösungsweg B: Mit dem Baumdiagramm berechnen
Mit der 1. Pfadregel ergibt sich:
2. Schritt: Gesamtanzahl der Städtereisen berechnen
Mit der Gesamtzahl der Kurzreisen aus der Aufgabenstellung folgt:
Lösungsweg B: Mit dem Baumdiagramm berechnen
Mit der 1. Pfadregel ergibt sich:
2. Schritt: Gesamtanzahl der Städtereisen berechnen
Mit der Gesamtzahl der Kurzreisen aus der Aufgabenstellung folgt:

 Insgesamt wurden damit
Insgesamt wurden damit  Millionen Städtereisen angetreten.
Millionen Städtereisen angetreten.
2.3
Lösungsweg A: Vierfeldertafel nutzen
Mit der Definition der bedingten Wahrscheinlichkeit folgt:
Damit handelt es sich zu ca.  um eine Auslandsreise.
Lösungsweg B: Baumdiagramm nutzen
Mit Hilfe des Satz von Bayes folgt:
Damit handelt es sich zu ca.
um eine Auslandsreise.
Lösungsweg B: Baumdiagramm nutzen
Mit Hilfe des Satz von Bayes folgt:
Damit handelt es sich zu ca.  um eine Auslandsreise.
um eine Auslandsreise.
3.1
Da die Nullhypothese  beträgt, ist der Test rechtsseitig. Es handelt sich um einen Test mit Alternativhypothese
beträgt, ist der Test rechtsseitig. Es handelt sich um einen Test mit Alternativhypothese  Stichprobenumfang
Stichprobenumfang  Signifikanzniveau
Signifikanzniveau  und binomialverteilter Zufallsvariable
und binomialverteilter Zufallsvariable  Damit folgt:
Mit Hilfe einer geeigneten Tabelle oder dem Taschenrechner folgt dann:
Damit folgt:
Mit Hilfe einer geeigneten Tabelle oder dem Taschenrechner folgt dann:


 Somit gilt
Somit gilt  Da der Test rechtsseitig ist, folgt damit für den Ablehnbereich
Da der Test rechtsseitig ist, folgt damit für den Ablehnbereich 
![\( =[c+1;100] \)](https://mathjax.schullv.de/892c9344c447949b2b3f1bb87546d454840bd725981dd95bd992ef9145b43814?color=5a5a5a)
![\( = [13+1;100] \)](https://mathjax.schullv.de/301c225325ffa52a7680dd85908fd430f647c9e107f5292ac69469ec3bd5db0e?color=5a5a5a)
![\( = [14;100]\)](https://mathjax.schullv.de/7a26afc22fa0d2eadc7b372a0fec1dba61ed50b37a26c3f7865c59e63f071d29?color=5a5a5a) und für den Annahmebereich
und für den Annahmebereich ![\(A=[0;13].\)](https://mathjax.schullv.de/bcb9b142fbee5c5e264f4605e5a46f645ff81651935ceb3230378d2403ead381?color=5a5a5a) Die Entscheidungsregel des Tests besagt also, dass davon ausgegangen wird, dass der Anteil der online gebuchten Pauschalreisen auf über
Die Entscheidungsregel des Tests besagt also, dass davon ausgegangen wird, dass der Anteil der online gebuchten Pauschalreisen auf über  gestiegen ist, wenn mindestens
gestiegen ist, wenn mindestens  der
der  Reisen online gebucht wurden.
Reisen online gebucht wurden.
Bei höchstens online gebuchten Reisen wird die Nullhypothese angenommen, das heißt die Reisebürokette geht davon aus, dass sich der Anteil der Online-Buchungen nicht erhöht hat.
online gebuchten Reisen wird die Nullhypothese angenommen, das heißt die Reisebürokette geht davon aus, dass sich der Anteil der Online-Buchungen nicht erhöht hat.
Bei höchstens
3.2.1
Fehler 1. Art im Sachzusammenhang erläutern
Der Fehler 1. Art tritt ein, wenn die Nullhypothese abgelehnt wird, obwohl diese in Wahrheit zutrifft, das heißt, wenn davon ausgegangen wird, dass sich der Anteil der online gebuchten Reisen erhöht hat, obwohl in der Realität nur höchstens  der Reisen online gebucht wurden.
Fehler 2. Art im Sachzusammenhang erläutern
Der Fehler 2.Art tritt ein, wenn die Nullhypothese angenommen wird, obwohl in diese in Wahrheit falsch ist, das heißt, wenn davon ausgegangen wird, dass die Wahrscheinlichkeit einer online gebuchten Reise immernoch höchstens
der Reisen online gebucht wurden.
Fehler 2. Art im Sachzusammenhang erläutern
Der Fehler 2.Art tritt ein, wenn die Nullhypothese angenommen wird, obwohl in diese in Wahrheit falsch ist, das heißt, wenn davon ausgegangen wird, dass die Wahrscheinlichkeit einer online gebuchten Reise immernoch höchstens  beträgt, diese in Wirklichkeit aber auf über
beträgt, diese in Wirklichkeit aber auf über  gestiegen ist.
gestiegen ist.
3.2.2
Mit der alternativen Wahrscheinlichkeit  aus der Aufgabenstellung ergibt sich mit Hilfe des binomCdf Befehls des CAS:
aus der Aufgabenstellung ergibt sich mit Hilfe des binomCdf Befehls des CAS:



_2015_c_l1b4_ti.png) Die Wahrscheinlichkeit, dass die Reisebürokette bei ihrem Hypothesentest einen Fehler 2. Art beging, liegt damit bei
Die Wahrscheinlichkeit, dass die Reisebürokette bei ihrem Hypothesentest einen Fehler 2. Art beging, liegt damit bei  .
.
_2015_c_l1b4_ti.png)
1.1
Wahrscheinlichkeit des ersten Ereignisses bestimmen
Die Zufallsvariable  ist binomialverteilt mit den Parametern
ist binomialverteilt mit den Parametern  und
und  und gibt die Anzahl der Reisen mit einem Reiseziel innerhalb Deutschlands an. Mit Hilfe des binomialPdf-Befehl des CAS folgt:
und gibt die Anzahl der Reisen mit einem Reiseziel innerhalb Deutschlands an. Mit Hilfe des binomialPdf-Befehl des CAS folgt:

_2015_c_l1b1_casio.png) Die Wahrscheinlichkeit, dass unter den
Die Wahrscheinlichkeit, dass unter den  Reisen genau
Reisen genau  ein Reiseziel innerhalb Deutschlands haben, beträgt ca.
ein Reiseziel innerhalb Deutschlands haben, beträgt ca.  Wahrscheinlichkeit des zweiten Ereignisses bestimmen
Mit Hilfe derselben Zufallsvariable
Wahrscheinlichkeit des zweiten Ereignisses bestimmen
Mit Hilfe derselben Zufallsvariable  wie beim ersten Ereignis folgt wieder mit dem binomialCdf-Befehl des CAS:
wie beim ersten Ereignis folgt wieder mit dem binomialCdf-Befehl des CAS:

_2015_c_l1b2_casio.png) Die Wahrscheinlichkeit, dass unter den
Die Wahrscheinlichkeit, dass unter den  Reisen mindestens
Reisen mindestens  ein Reiseziel innerhalb Deutschlands haben, beträgt ca.
ein Reiseziel innerhalb Deutschlands haben, beträgt ca.  Wahrscheinlichkeit des dritten Ereignisses bestimmen
Nun ist
Wahrscheinlichkeit des dritten Ereignisses bestimmen
Nun ist  eine binomialverteilte Zufallsgröße mit den Parametern
eine binomialverteilte Zufallsgröße mit den Parametern  und
und  die angibt, wieviele von den
die angibt, wieviele von den  betrachteten Reisen Fernreisen sind. Mit dem binomialPdf-Befehl des CAS folgt:
betrachteten Reisen Fernreisen sind. Mit dem binomialPdf-Befehl des CAS folgt:

_2015_c_l1b3_casio.png) Die Wahrscheinlichkeit, dass unter den
Die Wahrscheinlichkeit, dass unter den  Reisen mindestens sechs, aber höchstens acht Fernreisen sind, beträgt damit ca.
Reisen mindestens sechs, aber höchstens acht Fernreisen sind, beträgt damit ca. 
_2015_c_l1b1_casio.png)
_2015_c_l1b2_casio.png)
_2015_c_l1b3_casio.png)
1.2
Bedeutung der Gleichung erläutern
Die Gleichung gibt die Wahrscheinlichkeit dafür an, dass eine binomialverteilte Zufallsgröße  mit Parametern
mit Parametern  und
und  exakt den Wert
exakt den Wert  annimmt.
annimmt.
Da



 gilt, kann mit Hilfe der Wahrscheinlichkeiten aus der Aufgabenstellung geschlossen werden, dass
gilt, kann mit Hilfe der Wahrscheinlichkeiten aus der Aufgabenstellung geschlossen werden, dass  unter
unter  ausgewählten Reisen die Anzahl der Reisen mit Nah- und Mittelstreckenzielen angibt.
ausgewählten Reisen die Anzahl der Reisen mit Nah- und Mittelstreckenzielen angibt.
Die Gleichung besagt also im Sachzusammenhang, dass die Wahrscheinlichkeit dafür, dass unter zufällig ausgewählten Reisen genau
zufällig ausgewählten Reisen genau  Reisen Nah- oder Mittelstreckenziele haben,
Reisen Nah- oder Mittelstreckenziele haben,  beträgt.
beträgt.
Da
Die Gleichung besagt also im Sachzusammenhang, dass die Wahrscheinlichkeit dafür, dass unter
2.1
Lösungsweg A: Baumdiagramm zeichnen
Die Wahrscheinlichkeit für einen Kurzuralub im Ausland ergibt sich als Gegenereignis eines Kurzurlaubes im Inland wie folgt:





 Analog ergibt sich für Kurzurlaube im Inland, die Städtereisen sind:
Analog ergibt sich für Kurzurlaube im Inland, die Städtereisen sind:






 Da
Da  aller Kurzurlaube Städtereisen ins Ausland waren, folgt weiter:
Für Kurzurlaube ins Ausland, die keine Städtereisen waren, ergibt sich damit:
aller Kurzurlaube Städtereisen ins Ausland waren, folgt weiter:
Für Kurzurlaube ins Ausland, die keine Städtereisen waren, ergibt sich damit:






 Mit „I“ als Bezeichnung für Kurzurlaube im Inland, „S“ als Bezeichnung für Kurzurlaube, die Städtereisen sind und den Werten aus der Aufgabenstellung folgt:
Mit „I“ als Bezeichnung für Kurzurlaube im Inland, „S“ als Bezeichnung für Kurzurlaube, die Städtereisen sind und den Werten aus der Aufgabenstellung folgt:
 Lösungsweg B: Vierfeldertafel zeichnen
Die Wahrscheinlichkeit für eine Reise ins Ausland ergibt sich durch:
Lösungsweg B: Vierfeldertafel zeichnen
Die Wahrscheinlichkeit für eine Reise ins Ausland ergibt sich durch:





 Für die Wahrscheinlichkeit für eine Reise ins Ausland, die keine Städtereise ist, folgt:
Mit Hilfe der Wahrscheinlichkeit
Für die Wahrscheinlichkeit für eine Reise ins Ausland, die keine Städtereise ist, folgt:
Mit Hilfe der Wahrscheinlichkeit  aus der Aufgabenstellung folgt weiter:
Mit den Rechenregeln für die Vierfeldertafel und den Werten aus der Aufgabenstellung ergibt sich zudem:
Insgesamt folgt damit:
aus der Aufgabenstellung folgt weiter:
Mit den Rechenregeln für die Vierfeldertafel und den Werten aus der Aufgabenstellung ergibt sich zudem:
Insgesamt folgt damit:

| Städtereise | keine Städtereise | ||
|---|---|---|---|
| Ausland | |||
| Inland | |||
2.2
1. Schritt:  ermitteln
Lösungsweg A: Aus der Vierfeldertafel ablesen
ermitteln
Lösungsweg A: Aus der Vierfeldertafel ablesen
 Lösungsweg B: Mit dem Baumdiagramm berechnen
Mit der 1. Pfadregel ergibt sich:
2. Schritt: Gesamtanzahl der Städtereisen berechnen
Mit der Gesamtzahl der Kurzreisen aus der Aufgabenstellung folgt:
Lösungsweg B: Mit dem Baumdiagramm berechnen
Mit der 1. Pfadregel ergibt sich:
2. Schritt: Gesamtanzahl der Städtereisen berechnen
Mit der Gesamtzahl der Kurzreisen aus der Aufgabenstellung folgt:

 Insgesamt wurden damit
Insgesamt wurden damit  Millionen Städtereisen angetreten.
Millionen Städtereisen angetreten.
2.3
Lösungsweg A: Vierfeldertafel nutzen
Mit der Definition der bedingten Wahrscheinlichkeit folgt:
Damit handelt es sich zu ca.  um eine Auslandsreise.
Lösungsweg B: Baumdiagramm nutzen
Mit Hilfe des Satz von Bayes folgt:
Damit handelt es sich zu ca.
um eine Auslandsreise.
Lösungsweg B: Baumdiagramm nutzen
Mit Hilfe des Satz von Bayes folgt:
Damit handelt es sich zu ca.  um eine Auslandsreise.
um eine Auslandsreise.
3.1
Da die Nullhypothese  beträgt, ist der Test rechtsseitig. Es handelt sich um einen Test mit Alternativhypothese
beträgt, ist der Test rechtsseitig. Es handelt sich um einen Test mit Alternativhypothese  Stichprobenumfang
Stichprobenumfang  Signifikanzniveau
Signifikanzniveau  und binomialverteilter Zufallsvariable
und binomialverteilter Zufallsvariable  Damit folgt:
Mit Hilfe einer geeigneten Tabelle oder dem Taschenrechner folgt dann:
Damit folgt:
Mit Hilfe einer geeigneten Tabelle oder dem Taschenrechner folgt dann:


 Somit gilt
Somit gilt  Da der Test rechtsseitig ist, folgt damit für den Ablehnbereich
Da der Test rechtsseitig ist, folgt damit für den Ablehnbereich 
![\( =[c+1;100] \)](https://mathjax.schullv.de/892c9344c447949b2b3f1bb87546d454840bd725981dd95bd992ef9145b43814?color=5a5a5a)
![\( = [13+1;100] \)](https://mathjax.schullv.de/301c225325ffa52a7680dd85908fd430f647c9e107f5292ac69469ec3bd5db0e?color=5a5a5a)
![\( = [14;100]\)](https://mathjax.schullv.de/7a26afc22fa0d2eadc7b372a0fec1dba61ed50b37a26c3f7865c59e63f071d29?color=5a5a5a) und für den Annahmebereich
und für den Annahmebereich ![\(A=[0;13].\)](https://mathjax.schullv.de/bcb9b142fbee5c5e264f4605e5a46f645ff81651935ceb3230378d2403ead381?color=5a5a5a) Die Entscheidungsregel des Tests besagt also, dass davon ausgegangen wird, dass der Anteil der online gebuchten Pauschalreisen auf über
Die Entscheidungsregel des Tests besagt also, dass davon ausgegangen wird, dass der Anteil der online gebuchten Pauschalreisen auf über  gestiegen ist, wenn mindestens
gestiegen ist, wenn mindestens  der
der  Reisen online gebucht wurden.
Reisen online gebucht wurden.
Bei höchstens online gebuchten Reisen wird die Nullhypothese angenommen, das heißt die Reisebürokette geht davon aus, dass sich der Anteil der Online-Buchungen nicht erhöht hat.
online gebuchten Reisen wird die Nullhypothese angenommen, das heißt die Reisebürokette geht davon aus, dass sich der Anteil der Online-Buchungen nicht erhöht hat.
Bei höchstens
3.2.1
Fehler 1. Art im Sachzusammenhang erläutern
Der Fehler 1. Art tritt ein, wenn die Nullhypothese abgelehnt wird, obwohl diese in Wahrheit zutrifft, das heißt, wenn davon ausgegangen wird, dass sich der Anteil der online gebuchten Reisen erhöht hat, obwohl in der Realität nur höchstens  der Reisen online gebucht wurden.
Fehler 2. Art im Sachzusammenhang erläutern
Der Fehler 2.Art tritt ein, wenn die Nullhypothese angenommen wird, obwohl in diese in Wahrheit falsch ist, das heißt, wenn davon ausgegangen wird, dass die Wahrscheinlichkeit einer online gebuchten Reise immernoch höchstens
der Reisen online gebucht wurden.
Fehler 2. Art im Sachzusammenhang erläutern
Der Fehler 2.Art tritt ein, wenn die Nullhypothese angenommen wird, obwohl in diese in Wahrheit falsch ist, das heißt, wenn davon ausgegangen wird, dass die Wahrscheinlichkeit einer online gebuchten Reise immernoch höchstens  beträgt, diese in Wirklichkeit aber auf über
beträgt, diese in Wirklichkeit aber auf über  gestiegen ist.
gestiegen ist.
3.2.2
Mit der alternativen Wahrscheinlichkeit  aus der Aufgabenstellung ergibt sich mit Hilfe des binomialCdf Befehls des CAS:
aus der Aufgabenstellung ergibt sich mit Hilfe des binomialCdf Befehls des CAS:



_2015_c_l1b4_casio.png) Die Wahrscheinlichkeit, dass die Reisebürokette bei ihrem Hypothesentest einen Fehler 2. Art beging, liegt damit bei
Die Wahrscheinlichkeit, dass die Reisebürokette bei ihrem Hypothesentest einen Fehler 2. Art beging, liegt damit bei  .
.
_2015_c_l1b4_casio.png)