A – Wahlaufgaben

Analysis (Niveau 1)

Die Abbildung zeigt den Graphen $G_f$ einer in $\mathbb{R}$ definierten Funktion $f$ .

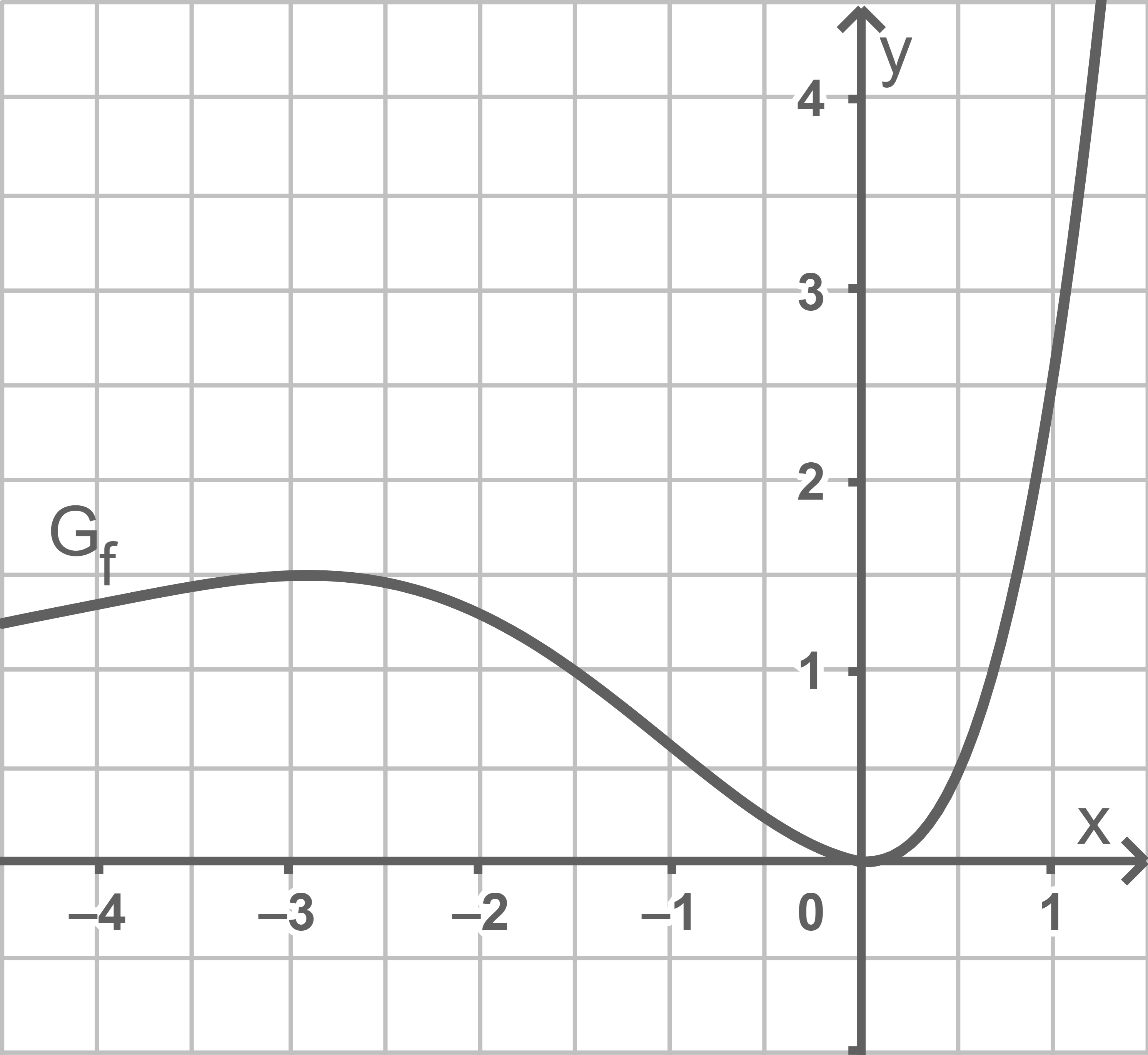
4.1

Bestimme grafisch den Wert des Integrals $\displaystyle\int_{-3}^{-1,5}f(x)\;\mathrm dx.$

(2 BE)

4.2

Beschreibe, wie der Graph der in $\mathbb{R}$ definierten Funktion $u$ mit $u(x) = -f(x) + 2$ aus $G_f$ erzeugt werden kann.

Gib die Koordinaten des Hochpunkts des Graphen von $u$ an.

(3 BE)

Lineare Algebra / Analytische Geometrie (Niveau 1)

Gegeben sind die Punkte $P(2\mid 0\mid 23)$ und $Q_t(6\mid t\mid 20)$ mit $t \in \mathbb{R}.$

5.1

Entscheide, ob es einen Wert von $t$ gibt, für den die Gerade $PQ_t$ parallel zur $xy$ -Ebene verläuft.

Begründe deine Entscheidung.

(2 BE)

5.2

Der Koordinatenursprung und die Punkte $P$ und $Q_t$ bilden ein Dreieck.

Ermittle diejenigen Werte von $t,$ für die das Dreieck in $Q_t$ einen rechten Winkel hat.

(3 BE)

Stochastik (Niveau 1)

Bei einem Dorffest in Bayern stammen $80\,\%$ der Gäste aus Bayern. $65\,\%$ aller Gäste tragen eine Tracht. Jede vierte Person unter den aus Bayern stammenden Gästen trägt keine Tracht.

Aus den Gästen wird zufällig eine Person ausgewählt, die nicht aus Bayern stammt.

Bestimme die Wahrscheinlichkeit, dass diese Person eine Tracht trägt.

(5 BE)

Analysis (Niveau 2)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x) = \dfrac{1}{2}x^2.$

Die Abbildung im Material zeigt den Graphen von $f$ sowie die Tangente $t$ an den Graphen von $f$ im Punkt $(4\mid f(4)).$

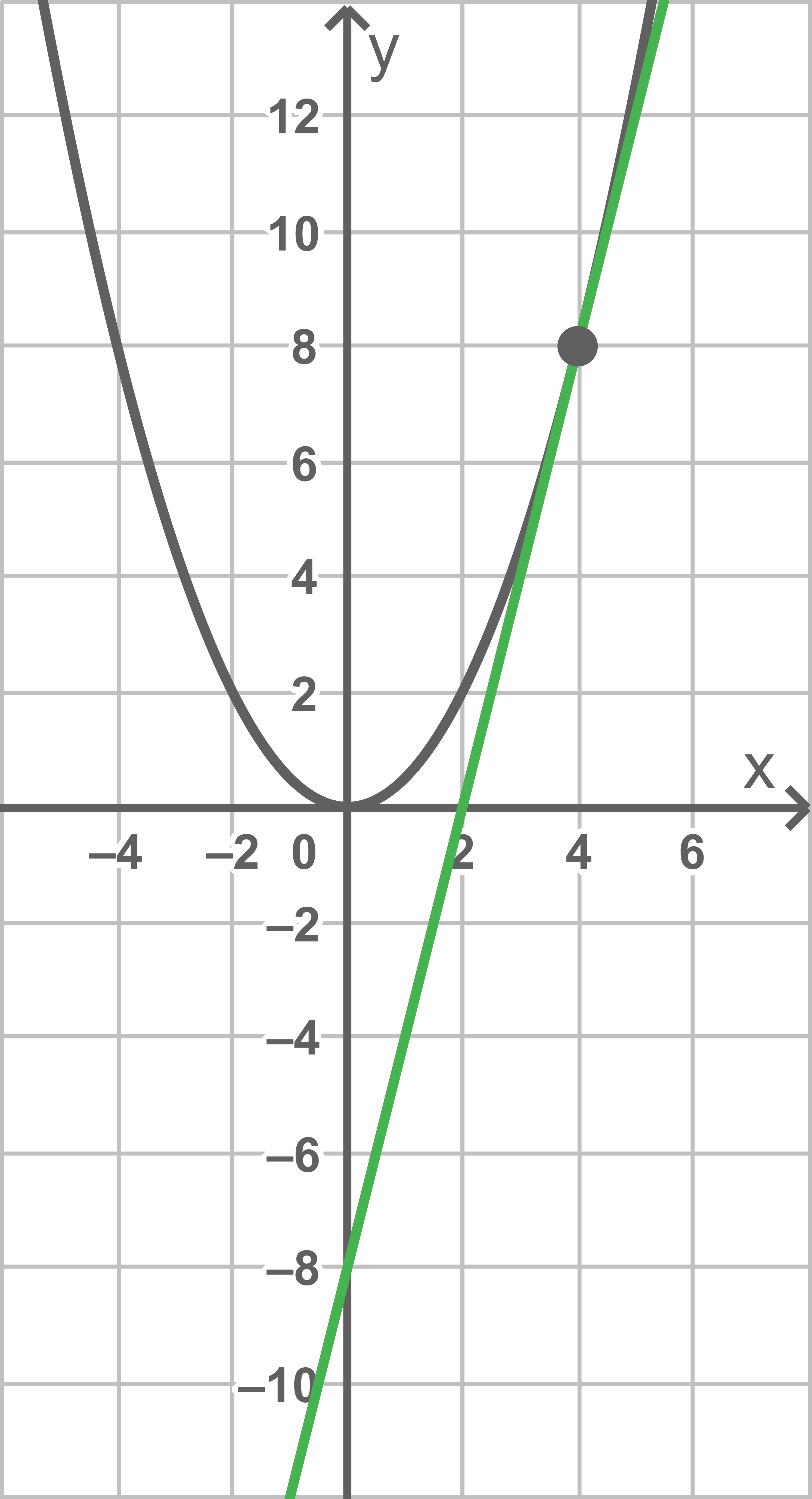
7.1

Gib anhand der Abbildung eine Gleichung der Tangente $t$ an.

(1 BE)

7.2

Weise nach, dass für jeden Wert $u \in \mathbb{R}$ die Tangente an den Graphen von $f$ im Punkt $(u\mid f(u))$ die $y$ -Achse im Punkt $(0\mid-f(u))$ schneidet.

(4 BE)

Lineare Algebra / Analytische Geometrie (Niveau 2)

Gegeben sind die Ebene $E: 2x - y - z = 5$ sowie der Punkt $P(1\mid 2 \mid 4).$ $P$ wird an der Ebene $E$ gespiegelt.

Berechne die Koordinaten des Bildpunktes $\(P$

(5 BE)

Stochastik (Niveau 2)

In einem Betrieb werden Geräte hergestellt, von denen jedes mit einer Wahrscheinlichkeit von $90\,\%$ fehlerfrei ist.

Bevor ein Gerät in den Verkauf gehen kann, wird es einer Endkontrolle unterzogen. Dabei identifiziert die Endkontrolle ein fehlerfreies Gerät mit einer Wahrscheinlichkeit von $99\,\%.$ Dagegen wird ein fehlerhaftes Gerät mit einer Wahrscheinlichkeit von $5\,\%$ ebenfalls als fehlerfrei eingestuft.

9.1

Zeige, dass die Wahrscheinlichkeit dafür, dass ein Gerät fehlerfrei ist und als fehlerfrei eingestuft wird, $89,1\,\%$ beträgt.

(2 BE)

9.2

Formuliere eine Aussage im Sachzusammenhang, die sich in Verbindung mit der Gleichung $0,891+0,1 \cdot 0,05=0,896$ aus der Ungleichung $\displaystyle\sum\limits_{k=90}^{100} \pmatrix{100\\k}\cdot 0,896^k\cdot 0,104^{100-k}\gt 0,5$ ergibt.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Analysis (Niveau 1)

4.1

Der Wert des Integrals gibt den Inhalt der Fläche zwischen dem Graphen und der $x$ -Achse zwischen den beiden Grenzen an. Im betrachteten Bereich sind das ungefähr 8 Kästchen, das heißt der Wert des Integrals ist etwa $8\cdot0,5^2=2\;[\text{FE}].$

4.2

Erzeugung des Graphen beschreiben

Der Graph von $u$ kann aus $G_f$ durch Spiegelung an der $x$ -Achse und anschließende Verschiebung um 2 in $y$ -Richtung erzeugt werden

Koordinaten des Hochpunkts angeben

Durch die Spiegelung an der $x$ -Achse wird aus dem Tiefpunkt von $G_f$ ein Hochpunkt. Die anschließende Verschiebung liefert somit die Koordinaten $H(0\mid 2)$ für den Hochpunkt des Graphen von $u.$

Lineare Algebra / Analytische Geometrie (Niveau 1)

5.1

Damit die Gerade $PQ$ parallel zur $xy$ -Ebene verläuft, müssen alle Punkte der Gerade die gleiche $z$ -Koordinate besitzen. Da die $z$ -Koordinaten von $P$ und $Q$ verschieden sind, existiert kein solches $t.$

5.2

Besitzt das Dreieck einen rechten Winkel in $Q_t,$ so gilt:

Rechenweg anzeigen

$\begin{array}[t]{rll} t_1&=&-6 \\[5pt] t_2&=&6 \end{array}$

Stochastik (Niveau 1)

$B \mathrel{\widehat{=}}$ Person stammt aus Bayern

$T \mathrel{\widehat{=}}$ Person trägt eine Tracht

Einsetzen der gegebenen Informationen in eine Vierfeldertafel liefert:

	$\color{#fff}{T}$	$\color{#fff}{\overline{T}}$	Gesamt
$\color{#fff}{B}$		$20 \,\%$	$80 \,\%$
$\color{#fff}{\overline{B}}$
Gesamt	$65 \,\%$		$100 \,\%$

Systematisches Ergänzen ergibt:

	$\color{#fff}{T}$	$\color{#fff}{\overline{T}}$	Gesamt
$\color{#fff}{B}$	$60 \,\%$	$20 \,\%$	$80 \,\%$
$\color{#fff}{\overline{B}}$	$5 \,\%$	$15 \,\%$	$20 \,\%$
Gesamt	$65 \,\%$	$35 \,\%$	$100 \,\%$

Für die Wahrscheinlichkeit, dass die gewählte Person, die nicht aus Bayern stammt, eine Tracht trägt, gilt also:

$P_{\overline{B}}(T)= \dfrac{5}{20} = 25 \,\%$

Analysis (Niveau 2)

7.1

Aus der Abbildung kann die Steigung $m=4$ sowie der $y$ -Achsenabschnitt bei $y=-8$ der Tangente abgelesen werden.

Eine Gleichung der Tangente ist somit $y=4x-8.$

7.2

$y$ -Koordinate angeben:

$f(u)=\dfrac{1}{2}u^2$

Ableitung von $f$ bestimmen:

$\(f$

Die Steigung $m$ der Tangente an der Stelle $u$ ergibt sich also zu:

$\(m=f$

Einsetzen der Steigung $m=u$ sowie der Koordinaten des Punktes $\left(u \; \bigg \vert\, \dfrac{1}{2}u^2\right)$ in die allgemeine Tangentengleichung liefert:

$\begin{array}[t]{rll} t: \quad y&=& m\cdot x+c& \\[5pt] \dfrac{1}{2}u^2 &=&u\cdot u + c &\quad \scriptsize \mid\;-u^2 \\[5pt] -\dfrac{1}{2}u^2&=& c \end{array}$

Somit schneidet die Tangente die $y$ -Achse an der Stelle $c=-\dfrac{1}{2}u^2=-f(u)$ und folglich im Punkt $(0\mid-f(u)).$

Lineare Algebra / Analytische Geometrie (Niveau 2)

1. Schritt: Hilfsgerade $\boldsymbol{h}$ aufstellen

Eine Gleichung der Geraden, die senkrecht auf $E$ steht und durch den Punkt $P$ verläuft, ergibt sich mit einem Normalenvektor $\overrightarrow{n_E}$ von $E$ zu:

$\begin{array}[t]{rll} h: \; \overrightarrow{x}&=& \overrightarrow{OP}+s \cdot \overrightarrow{n_E} & \\[5pt] &=& \pmatrix{1\\2\\4}+s \cdot \pmatrix{2\\-1\\-1} \end{array}$

2. Schritt: Schnittpunkt bestimmen

Der Lotfußpunkt $L$ der Gerade $h$ auf die Ebene $E$ ergibt sich durch Einsetzen des allgemeinen Geradenpunkts von $h$ in $E:$

$s=1,5$

Rechenweg anzeigen

Einsetzen in den allgemeinen Geradenpunkt liefert:

$\overrightarrow{OL}=\pmatrix{1+2 \cdot 1,5\\2-1 \cdot 1,5\\4-1\cdot 1,5}=\pmatrix{4\\0,5\\2,5}$

3. Schritt: Koordinaten des Bildpunkts berechnen

Es gilt:

$\(\begin{array}[t]{rll} \overrightarrow{OP$

Die Koordinaten des Bildpunktes $\(P$ sind somit gegeben durch $(7 \mid -1 \mid 1).$

Stochastik (Niveau 2)

9.1

Aus der Aufgabenstellung folgt:

Wahrscheinlichkeit, dass ein Gerät fehlerfrei ist: $P (\text{fehlerfrei})=0,90$

Wahrscheinlichkeit, dass ein fehlerfreies Gerät als fehlerfrei eingestuft wird: $P (\text { erkannt } \mid \text { fehlerfrei }) =0,99$

$P(\text { fehlerfrei und erkannt })=0,891$

Rechenweg anzeigen

9.2

Die erste Gleichung beschreibt die Gesamtwahrscheinlichkeit, dass ein Gerät als fehlerfrei eingestuft wird, unabhängig davon, ob es tatsächlich fehlerfrei ist oder nicht.

Die Summenformel beschreibt somit die Wahrscheinlichkeit, dass in einer Stichprobe von 100 Geräten mindestens 90 Geräte als fehlerfrei erkannt werden.

„Da ein kleiner Anteil fehlerhafter Geräte ebenfalls als fehlerfrei eingestuft wird, ist es wahrscheinlicher, dass mindestens $90\,\%$ der Geräte aus der Stichprobe von 100 Geräten als fehlerfrei erkannt werden, als dass weniger als die erwarteten $90\,\%$ der Geräte als fehlerhaft eingestuft werden.“

Alternative Lösung:

"Mit einer Wahrscheinlichkeit von über $50\,\%$ werden in einer Stichprobe von 100 Geräten mindestens 90 Geräte als fehlerfrei erkannt werden, da ein kleiner Anteil fehlerhafter Geräte ebenfalls als fehlerfrei eingestuft wird."

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?