B1 - Analytische Geometrie

Vor dem Firmengebäude der Firma Kugel Glasbau steht zu Werbezwecken eine gläserne Pyramide mit quadratischer Grundfläche (Material).

In einem an dem Gebäude orientierten Koordinatensystem sind die Punkte $A(10\mid 2\mid 0), B(18\mid 8\mid 0)$ und $C(12\mid 16\mid 0)$ drei der Eckpunkte der Pyramidengrundfläche. Die Spitze der Pyramide befindet sich in der Höhe $h = 10\,\text{m}$ senkrecht über der Mitte der Pyramidengrundfläche.

Eine Längeneinheit entspricht einem Meter.

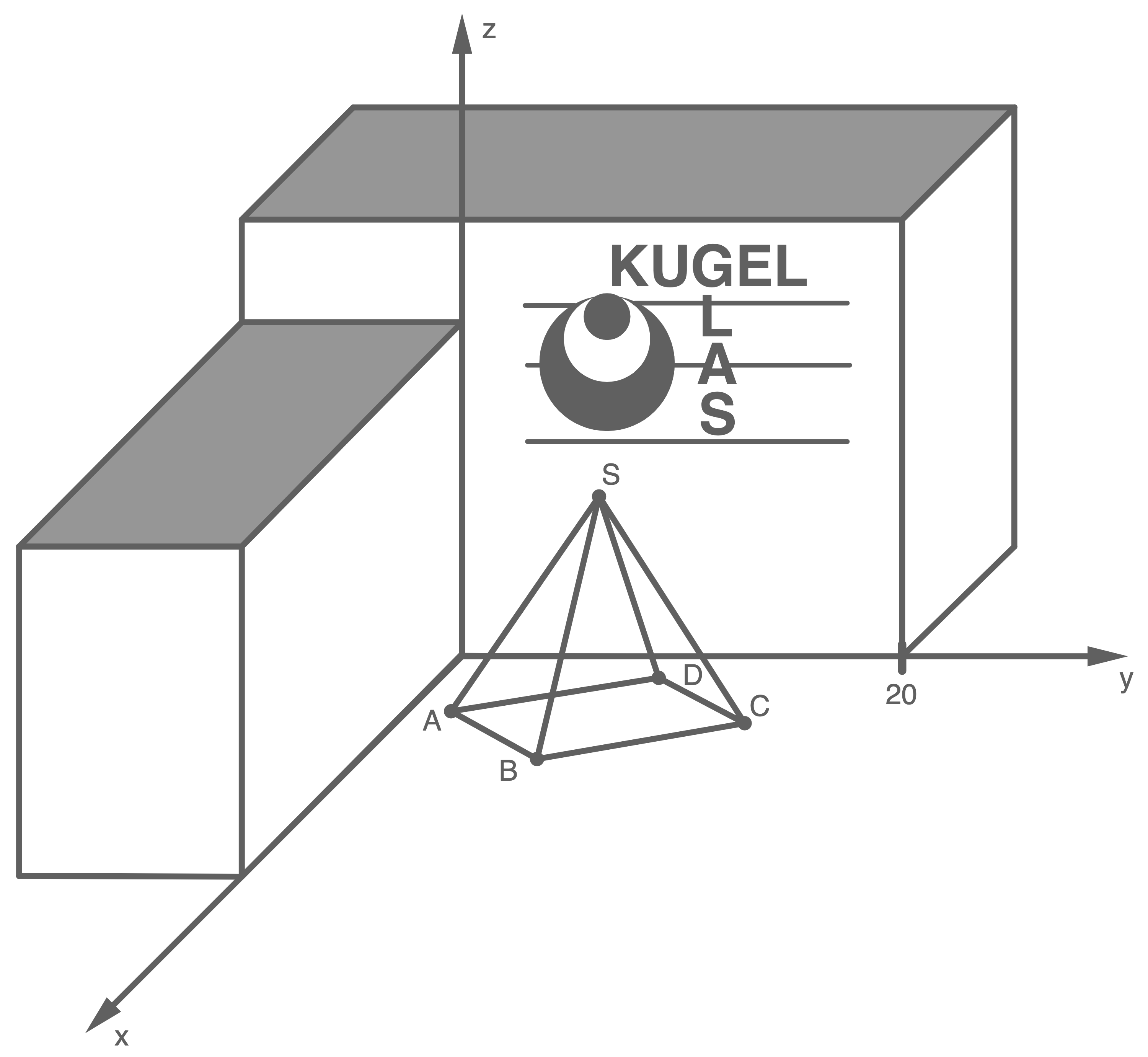
B1 - Analytische Geometrie Firmengebäude

1.1

Berechne die Koordinaten des Eckpunkts $D$ der Pyramidengrundfläche und die Koordinaten der Spitze $S$ der Pyramide.

$\big[$ Zur Kontrolle: $S\;(11\mid 9\mid 10) \big]$

(4 BE)

1.2

Die von jedem der Eckpunkte $A, B, C$ und $D$ jeweils zur Spitze $S$ verlaufenden Seitenkanten der Pyramide sind durch Metallschienen verstärkt. Berechne die Gesamtlänge aller Schienen.

(2 BE)

Die Eckpunkte $A$ und $B$ sowie die Spitze $S$ liegen in einer Ebene $E_{ABS}.$

2.1

Bestimme eine Koordinatengleichung der Ebene $E_{ABS}.$

$\big[$ Zur Kontrolle: Eine mögliche Koordinatengleichung von $E_{ABS}$ lautet $\;6x - 8y + 5z = 44. \big]$

(5 BE)

2.2

Eine benachbarte Seitenfläche enthält die Punkte $A,D$ und $S$ und liegt in der Ebene $E_{ADS}: 8x + 6y - 5z = 92.$

Berechne den Schnittwinkel der Ebenen $E_{ABS}$ und $E_{ADS}.$

(4 BE)

Im Inneren der Pyramide ist in Anlehnung an das Firmenlogo eine Kugel mit einem Durchmesser von $4\;\text{m}$ so aufgehängt, dass der Kugelmittelpunkt in einem Abstand von $5\,\text{m}$ vertikal unterhalb der Pyramidenspitze $S$ liegt.

3.1

Erkläre, warum der Punkt $M(11\mid 9\mid 5)$ der Mittelpunkt der Kugel ist.

(2 BE)

3.2

Untersuche, ob die Kugel die Seitenflächen der Pyramide berührt.

(6 BE)

Um einen besseren Werbeeffekt zu erzielen, soll die Pyramide abends beleuchtet werden. Die Lichtquelle befindet sich im Punkt $P(a\mid 0\mid 0)$ mit $a \gt 0.$ Der Schatten der Pyramide fällt dabei auf den $20\,\text{m}$ hohen und $30\,\text{m}$ breiten, größeren Teil des Firmengebäudes.

4.1

Zeichne einen der Punkte $P(a\mid 0\mid 0)$ sowie einen der Punkte $Q(0\mid y\mid 20)$ mit $0 \lt y \leq 20$ in das Koordinatensystem im Material.

(2 BE)

4.2

Erläutere die Rechenschritte in den Zeilen (1) bis (3) und deute das Ergebnis in Zeile (4) im Sachzusammenhang.

(1)

$S(11\mid 9\mid 10);$ $\overrightarrow{x}=\pmatrix{a\\0\\0} + t\cdot \pmatrix{11-a\\9\\10}$

(2)

$Q(0\mid y \mid 20);$

$\begin{array}{l|rl|l} \text{I}\quad&a+11t-a\cdot t=& 0 \\ \text{II}\quad&9t=& y \\ \text{III}\quad&10t=&20 & \Leftrightarrow t=2 \\ \end{array}$

(3)

$a+22-2a=0\,\Leftrightarrow\, a=22$

(4)

also: $P(22\mid 0\mid0)$

(5 BE)

1.1

Koordinaten des Eckpunktes $D$ berechnen

Da die Grundfläche quadratisch ist, entspricht der Verbindungsvektor $\overrightarrow{BA}$ dem gegenüberliegenden Verbindungsvektor $\overrightarrow{CD}.$ Der Ortsvektor von $D$ ergibt sich somit zu:

Rechenweg anzeigen

$\overrightarrow{OD} = \pmatrix{4\\10\\0}$

Die Koordinaten von $D$ lauten $D(4\mid 10\mid 0).$

Koordinaten der Spitze $S$ berechnen

Die Spitze $S$ befindet sich senkrecht über dem Mittelpunkt $M$ der quadratischen Grundfläche.
Mit der Formel für den Mittelpunkt einer Strecke folgt:

Rechenweg anzeigen

$\overrightarrow{OM_{AC}} = \pmatrix{11 \\ 9 \\ 0}$

Die Spitze befindet sich in einer Höhe von $h=10\,\text{m},$ somit beträgt die $z$ -Koordinate von $S$ gerade $10.$

Die Koordinaten von $S$ lauten damit $S(11\mid 9\mid 10).$

1.2

Da die Pyramide eine quadratische Grundfläche besitzt und die Spitze direkt senkrecht über dem Mittelpunkt dieser Grundfläche liegt, sind alle vier Seitenkanten gleich lang. Es genügt somit die Länge der Strecke $\overline{AS}$ zu berechnen. Mit Verwendung des norm-Befehls des CAS für den Vektorbetrag folgt:

$\left|\overrightarrow{AS} \right|$ $= \left|\pmatrix{1\\7\\10} \right|$ $= \sqrt{1^2+7^2+10^2}$ $= \sqrt{150}$

Die Gesamtlänge aller Schienen beträgt somit $4\cdot \sqrt{150} \approx 48,99\,\text{m}.$

2.1

Koordinatengleichung bestimmen

Ein Normalenvektor der Ebene $E_{ABS}$ folgt mit dem crossP-Befehl des CAS:

Rechenweg anzeigen

$\overrightarrow{n} = \pmatrix{6\\-8 \\ 5}$

Durch Verwendung des gekürzten Vektors und Einsetzen der Koordinaten von $S$ folgt:

Rechenweg anzeigen

$d = 44$

Eine Koordinatengleichung von $E_{ABS}$ lautet somit $E_{ABS}: \, 6x -8y +5z = 44.$

2.2

Mit Hilfe der Normalenvektoren der Ebenen folgt:

Rechenweg anzeigen

$\alpha \approx 78,5^{\circ}$

Der Schnittwinkel der Ebenen $E_{ABS}$ und $E_{ADS}$ beträgt ca. $78,5^{\circ}.$

3.1

Da der Mittelpunkt der Kugel vertikal unterhalb der Pyramidenspitze liegt, besitzt er die gleiche $x$ - und $y$ -Koordinate wie $S.$ Der Mittelpunkt liegt $5\;\text{m}$ unterhalb der Spitze. Die $z$ -Koordinate ergibt sich somit mit Hilfe der $z$ -Koordinate von $S$ zu $10-5 = 5.$ Insgesamt gilt also für die Koordinaten des Mittelpunktes der Kugel $M(11\mid 9\mid 5).$

3.2

Durch die Lage der Kugel innerhalb der quadratischen Pyramide, genügt es eine Seitenfläche auf die Berührung der Kugel zu überprüfen.
Die Kugel berührt die Seitenfläche, wenn der Abstand des Mittelpunkts zur zugehörigen Ebene gleich dem Radius der Kugel ist.

Mit Verwendung der Hesseschen Normalform der Ebene $E_{ABS}$ folgt:

Rechenweg anzeigen

$E_{ABS} ...$

Einsetzen der Koordinaten des Mittelpunkts liefert:

Rechenweg anzeigen

$d(E_{ABS},M) \approx 2,24$

Der Mittelpunkt der Kugel ist somit von den Seitenflächen ca. $2,24\,\text{m}$ entfernt. Die Kugel berührt die Seitenflächen also nicht.

4.1

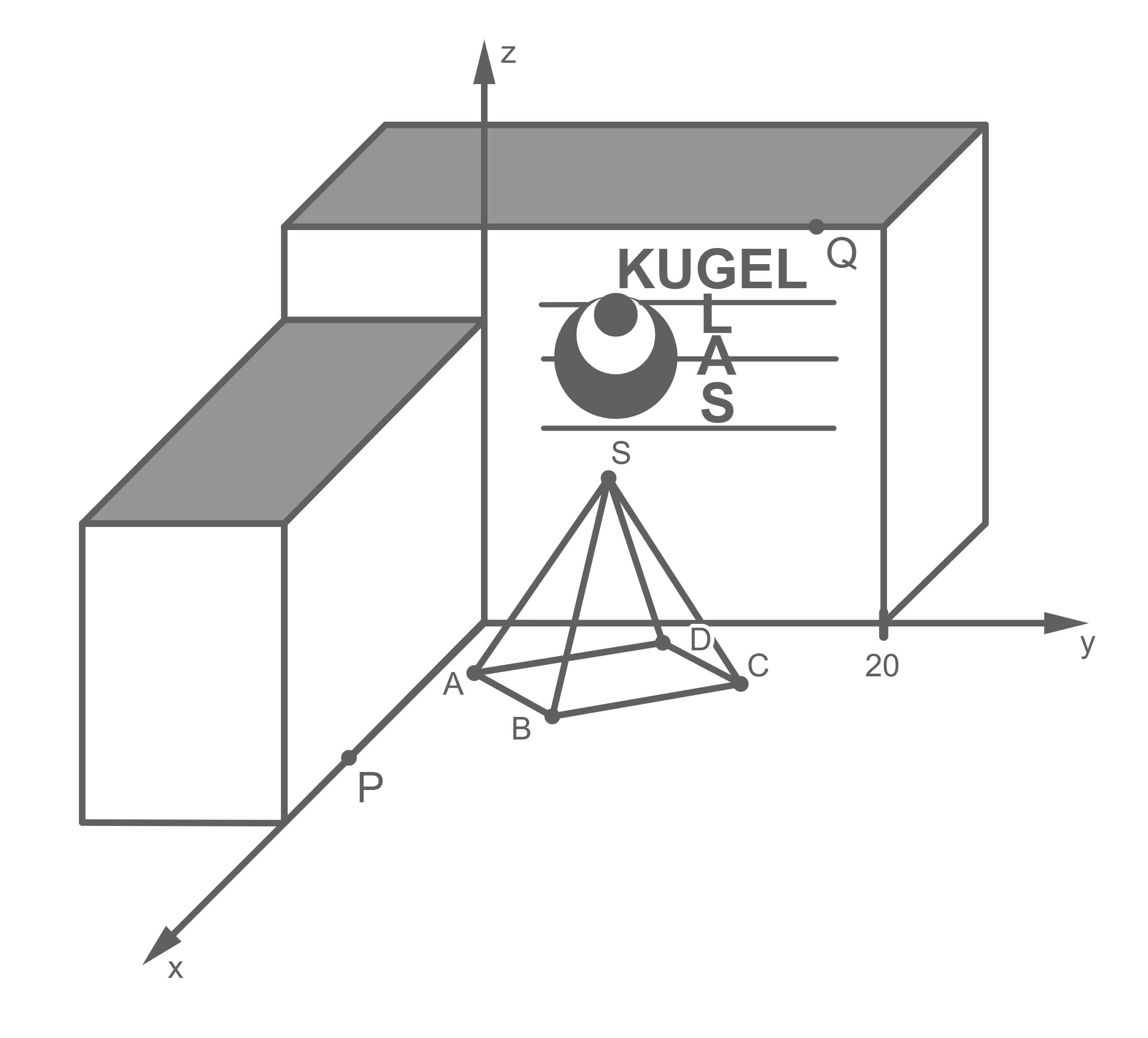
Eine mögliche Lösung für die Punkte $P$ und $Q$

4.2

(1)

In Schritt (1) wird eine Gleichung der Gerade aufgestellt, entlang derer sich das Licht bewegt, das von der Lichtquelle im Punkt $P(a\mid0\mid0)$ aus an der Pyramidenspitze im Punkt $S$ entlang verläuft.

(2)

Der Punkt $Q$ liegt für $0\leq y \leq 20$ auf der oberen Kante des Firmengebäudeteils, auf den der Schatten fällt. Durch Einsetzen der Koordinaten von $Q$ in die Geradengleichung aus (1) entsteht ein Gleichungssystem mit drei Gleichungen in Abhängigkeit von $a,$ $t$ und $y.$ Aus der dritten Gleichung folgt direkt $t=2.$

(3)

Die Lösung für $t$ aus (2) wird in die erste Gleichung des Gleichungssystems eingesetzt. Mit Hilfe derer folgt $a=22.$

(4)

In (1) bis (3) wird der Wert von $a$ berechnet, für den der Schatten der Pyramidenspitze auf der oberen Kante des Gebäudeteils liegt.
Der Punkt $P(22\mid 0\mid0)$ ist somit der Punkt, in dem sich die Lichtquelle befinden muss, damit der Schatten der Pyramidenspitze auf der oberen Kante des Gebäudeteils liegt, auf den der Schatten fällt.