A - Hilfsmittelfreier Teil

Stochastik - Niveau 1

Eine Urne enthält $3$ rote und $5$ gelbe Kugeln.

1.1

Es werden nacheinander zwei Kugeln ohne Zurücklegen gezogen.
Berechne die Wahrscheinlichkeit $p_{1}$ , dass die beiden Kugeln gelb sind.
Gib die Wahrscheinlichkeit $p_{2}$ dafür an, dass die zweite Kugel gelb ist, wenn die erste Kugel bereits gelb war.

(2 BE)

1.2

Es werden nacheinander $5$ Kugeln mit Zurücklegen gezogen.
Erläutere im Sachzusammenhang, was mit dem folgenden Term berechnet wird. Gehe dabei auf die einzelnen Faktoren des Terms ein.
$\pmatrix{5\\2}\cdot \left(\dfrac{3}{8}\right)^2\cdot \left(\dfrac{5}{8}\right)^3$

(3 BE)

Analysis- Niveau 1

Gegeben ist die Funktion $f$ mit $f(x)=(x^{2}-x)\cdot \mathrm e^{x}$ .

2.1

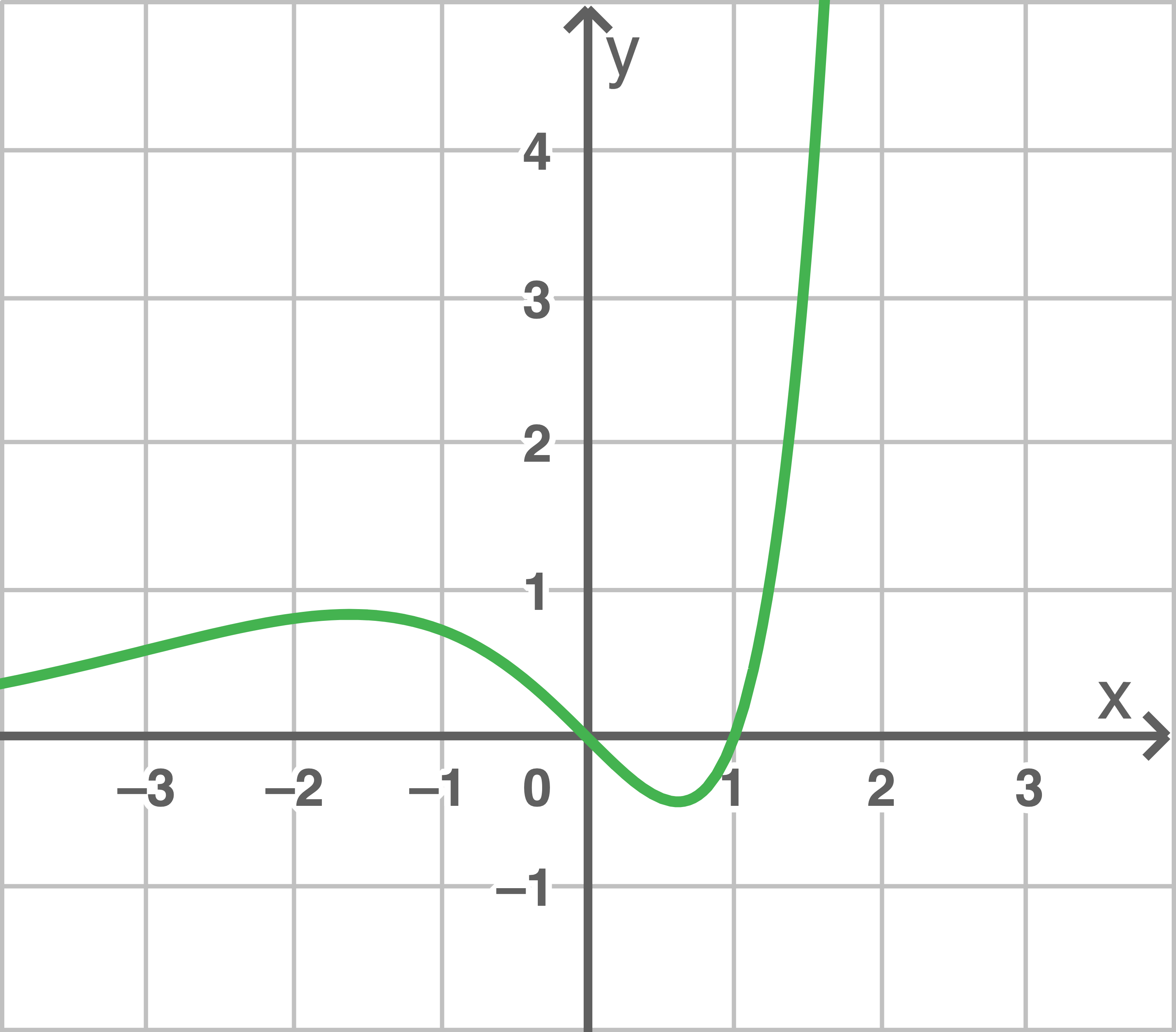
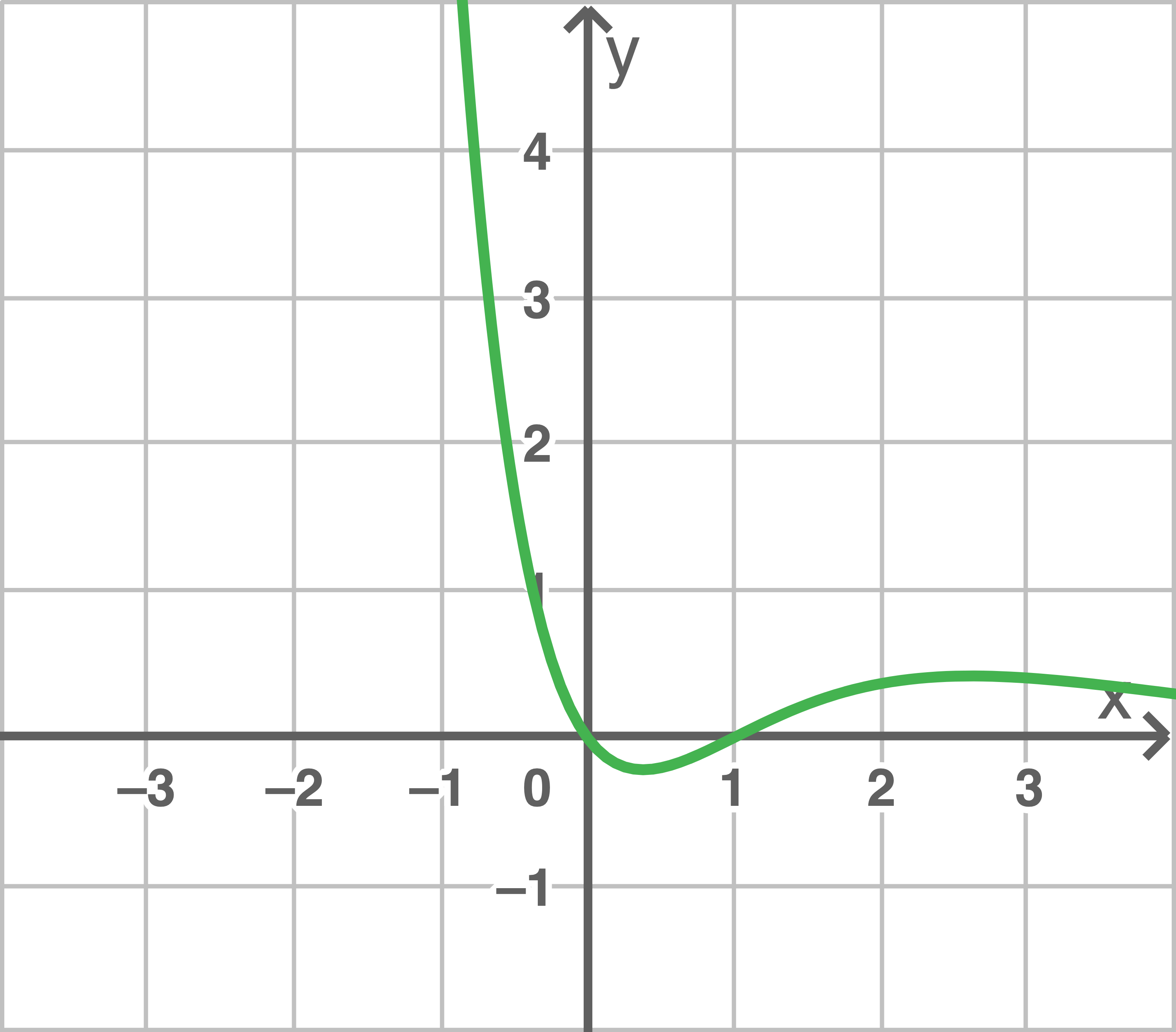
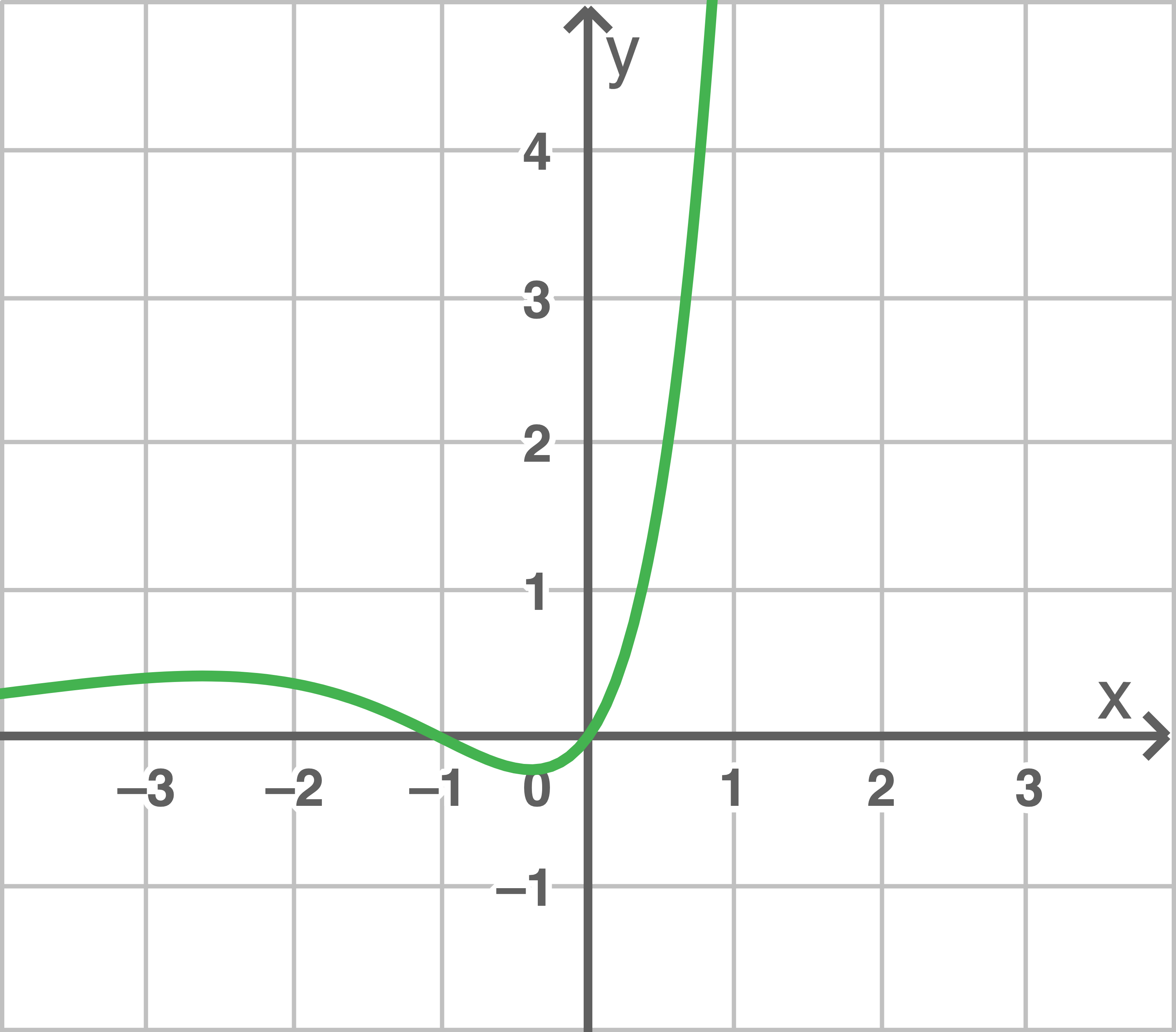
Entscheide, welcher der drei dargestellten Graphen zur Funktion $f$ gehört.

Graph (I)

Graph (II)

Graph (III)

(3 BE)

2.2

Ermittle die Funktionsgleichung der Ableitungsfunktion $\(f$ .
Hinweis: Ein Vereinfachen des Funktionsterms ist nicht erforderlich.

(2 BE)

Lineare Algebra/Analytische Geometrie - Niveau 1

Berechne die Lösung des folgenden Iinearen Gleichungssystems:

$\begin{array}{lrll} \text{I}\quad&2x-3y+2z&=&0 &\quad \\ \text{II}\quad&-2x+y-z&=&-1 &\quad \\ \text{III}\quad&6x-10y+2z&=&-14 &\quad \\ \end{array}$

(5 BE)

Lineare Algebra/Analytische Geometrie - Niveau 2

Gegeben ist die Ebene $E$ mit der Koordinatengleichung $E:x+z=-3.$

4.1

Bestimme die Koordinaten der Schnittpunkte von $E$ mit den Koordinatenachsen und gib die besondere Lage von $E$ im Koordinatensystem an.

(3 BE)

4.2

Gegeben ist weiterhin die Gerade, $g:\overrightarrow{x}= \pmatrix{0\\0\\1}+t \cdot\pmatrix{-1\\0\\1}$ $,\,t\in \mathbb{R}$ .
Untersuche die besondere Lage von $g$ sowohl zu $E$ als auch im Koordinatensystem.

(2 BE)

Stochastik - Niveau 1

1.1

Insgesamt beinhaltet die Urne 8 Kugeln, sodass die Anfangswahrscheinlichkeit für eine rote Kugel $p_r= \dfrac{3}{8}$ und für eine gelbe Kugel $p_g=\dfrac{5}{8}$ beträgt.
Gezogen wird zweimal ohne Zurücklegen, womit sich folgendes Baumdiagramm ergibt:

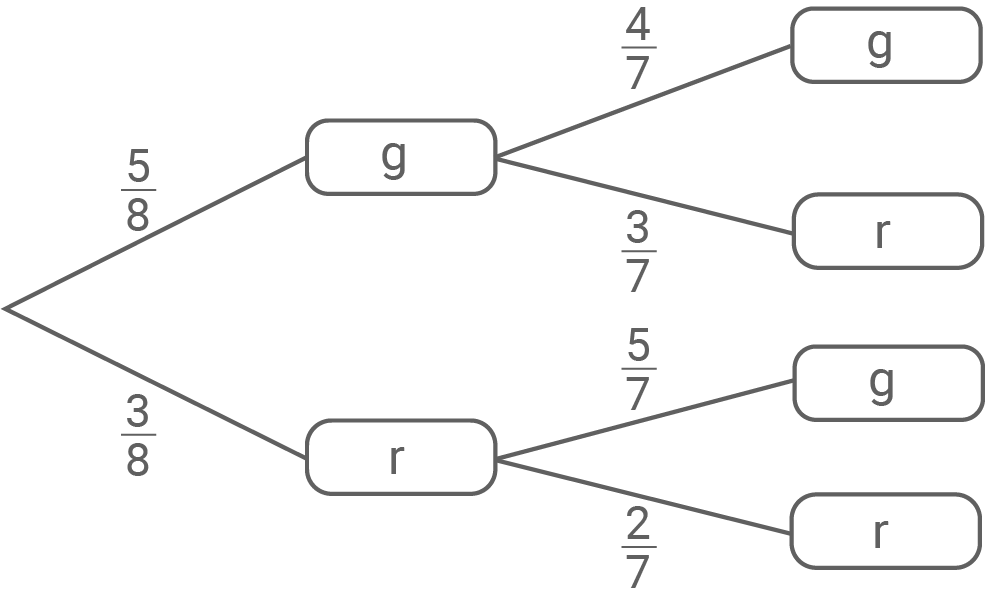Mit der ersten Pfadregel ergibt sich die Wahrscheinlichkeit für das Ereignis $p_1$ :

$p_1 = \dfrac{5}{8} \cdot \dfrac{4}{7}= \dfrac{20}{56} = \dfrac{5}{14}$

Aus dem Baumdiagramm folgt:

$p_2 = \dfrac{4}{7}$

1.2

Der Term $\pmatrix{n\\k}\cdot p^k \cdot p^{n-k} =\pmatrix{5\\2}\cdot \pmatrix{\dfrac{3}{8}}^2 \cdot \pmatrix{\dfrac{5}{8}}^3$ berechnet die Wahrscheinlichkeit, dass beim fünfmaligen Ziehen mit Zurücklegen genau zwei rote Kugeln gezogen werden.

$\pmatrix{5\\2}$ gibt die Anzahl der Pfade mit 2 roten und 3 gelben Kugeln an.
$\pmatrix{\dfrac{3}{8}}^2$ gibt die Wahrscheinlichkeit, 2 rote Kugeln hintereinander zu ziehen an.
$\pmatrix{\dfrac{5}{8}}^3$ gibt die Wahrscheinlichkeit, 3 gelben Kugeln hintereinander zu ziehen an.

Analysis - Niveau 1

2.1

Die Graphen unterscheiden sich in den Nullstellen.

$\begin{array}[t]{rll} f(x)&=& 0&\quad \scriptsize \\[5pt] (x^2 -x) \cdot \mathrm e^x&=& 0 & \\[5pt] x\cdot (x - 1)\cdot \mathrm e^x&=& 0 &\quad \scriptsize \\[5pt] \end{array}$

Da stets $\mathrm e^x\neq0$ gilt, folgt mit dem Satz vom Nullprodukt $x_1=0$ und $x-1=0.$

$\begin{array}[t]{rll} x-1&=& 0 &\quad \scriptsize\mid +1 \\[5pt] x_2&=&1 &\quad \scriptsize \\ \end{array}$

Die Nullstellen der Funktion sind folglich bei $x_1=0$ und $x_2=1$ .

(II) lässt sich ausschließen, da $\lim\limits_{x\to\infty} f(x) \neq \infty$ , denn der Graph nähert sich der $x$ -Achse immer weiter an.

(III) passt nicht, da die Nullstellen nicht übereinstimmen.

Der Graph zu $f(x)$ ist (I).

2.2

Mit der Produktregel folgt:

$\begin{array}[t]{rll} f(x)&=& (x^2 -x) \cdot \mathrm e^x & \quad \scriptsize \\[5pt] f‘(x)&=& (x^2 -x)\cdot \mathrm e^x+ (2x -1) \cdot \mathrm e ^x & \quad \scriptsize \\[5pt] \end{array}$

Lineare Algebra/Analytische Geometrie - Niveau 1

LGS lösen:

$\begin{array}{lrll} \text{I}\quad&0&=&2 x -3 y +2z &\quad \scriptsize\mid\;\text{ }\text{I}+\text{II}\\ \text{II}\quad&-1&=&-2x+y-z &\quad \\ \text{III}\quad&-14&=&6x-10y+2z &\quad \\ \hline \text{I‘}\quad&-1&=& -2 y + z &\quad \\ \text{II}\quad&-1&=&-2x+y-z &\quad \scriptsize\mid\;\text{3}\cdot \text{II}-\text{III} \\ \text{III}\quad&-14&=&6x-10y+2z &\quad \\ \hline \text{I ‘}\quad&-1&=& -2 y + z &\quad \scriptsize\mid\;\text{ }\text{I}+\text{II}\\ \text{II‘}\quad&-17&=&-7y-z &\quad \\ \text{III}\quad&-14&=&6x-10y+2z &\quad \\ \hline \text{I ‘‘}\quad&-18&=& -9 y &\quad \\ \text{II‘}\quad&-17&=&-7y-z &\quad \\ \text{III}\quad&-14&=&6x-10y+2z &\quad \\ \end{array}$

Aus $\(\text{I$ ergibt sich:

$\begin{array}[t]{rll} -18&=& -9y &\quad \scriptsize \mid\ :(-9) \\[5pt] 2&=& y \end{array}$

Aus $\(\text{II$ ergibt sich:

$\begin{array}[t]{rll} -17&=& -7y-z&\quad \scriptsize \mid\ y=2 \\[5pt] -17&=& -14-z&\quad \scriptsize \mid\ +14 \\[5pt] 3&=& z \end{array}$

Aus $\text{III}$ ergibt sich:

$\begin{array}[t]{rll} -14&=& 6x-10y+2z &\quad \scriptsize \mid\ z=3, y=2 \\[5pt] -14&=& 6x-10 \cdot 2+2\cdot 3 \\[5pt] -14&=& 6x-14&\quad \scriptsize \mid-14 \\[5pt] 0&=& x \end{array}$

Lineare Algebra/Analytische Geometrie - Niveau 2

4.1

Schnittpunkt mit Achsen überprüfen:

Mit $P_x= \pmatrix{x\\0\\0}$ folgt $x+0=-3$ , d.h. die Koordinaten des Schnittpunktes mit der $x$ -Achse lauten $S_x=\pmatrix{-3\\0\\0}.$

Mit $P_y= \pmatrix{0\\y\\0}$ folgt $0+0\neq-3$ , es gibt somit keinen Schnittpunkt mit der $y$ -Achse.

Einsetzen von $P_z= \pmatrix{0\\0\\z}$ ergibt $0+z=-3 .$

Die Koordinaten des Schnittpunktes sind $S_z=\pmatrix{0\\0\\-3}.$

Besondere Lage: Die Ebene $E$ verläuft parallel zur $y$ -Achse.

4.2

Aus der Geraden $g$ können $x=-t$ und $z=1+t$ abgelesen und in $E$ eingesetzt werden:

$\begin{array}[t]{rll} E:x+z&=& -3&\quad \scriptsize \\[5pt] -t+(1+t)&=& -3\\[5pt] -t+1+t&=& -3\\[5pt] 1&\neq&-3 \quad \scriptsize \\[5pt] \end{array}$

Da es sich um eine Ungleichung handelt, die kein Ergebnis hat, lässt sich daraus schließen, dass die Gerade $g$ parallel zur Ebene $E$ ist.

Die $y$ -Koordinate des Stützvektors und des Richtungsvektors der Geraden sind gleich null, weswegen die Gerade in der $xz$ -Ebene verläuft.