A1 - Analysis
Eine Käferpopulation besteht zu einem bestimmten Anfangszeitpunkt aus  Exemplaren. Zwar kommen jedes Jahr durch Fortpflanzung neue Käfer hinzu, gleichzeitig wird die Population aber durch natürliche Feinde dezimiert.
Exemplaren. Zwar kommen jedes Jahr durch Fortpflanzung neue Käfer hinzu, gleichzeitig wird die Population aber durch natürliche Feinde dezimiert.
Die Entwicklung der Käferpopulation kann durch die folgende Funktion beschrieben werden:
beschrieben werden:

Dabei gilt Folgendes:
1 Einheit der Funktionswerte Käfer
Käfer
1 Einheit der -Werte
-Werte  Jahr
Im Material ist der Graph von
Jahr
Im Material ist der Graph von  abgebildet.
abgebildet.
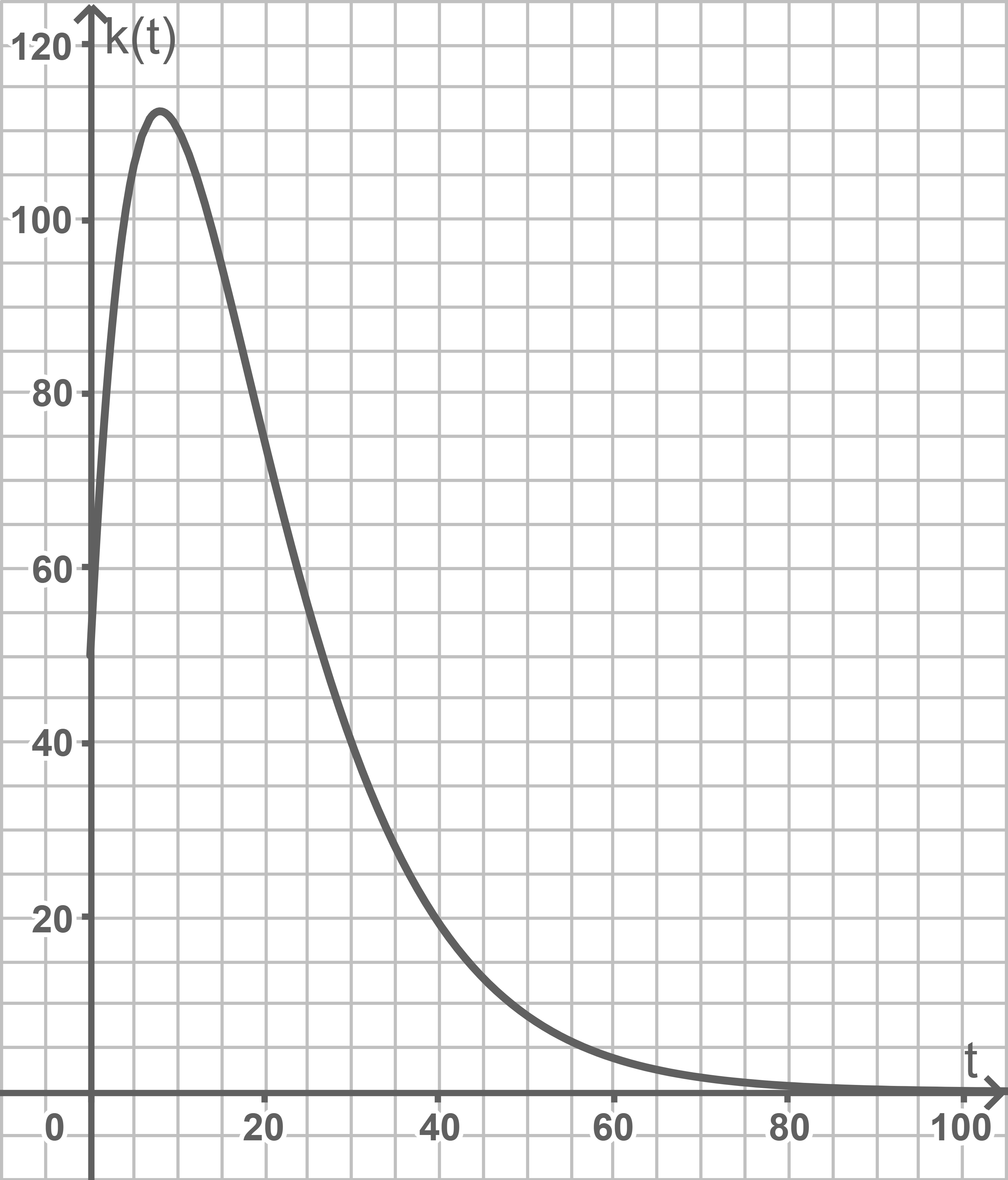
Die Entwicklung der Käferpopulation kann durch die folgende Funktion
Dabei gilt Folgendes:
1 Einheit der Funktionswerte
1 Einheit der
1.
Berechne ohne Bezugnahme auf den Graphen von  die Extrem- und Wendepunkte des Graphen innerhalb des betrachteten Intervalls unter Zuhilfenahme der ersten Ableitung
die Extrem- und Wendepunkte des Graphen innerhalb des betrachteten Intervalls unter Zuhilfenahme der ersten Ableitung 
Begründe das Grenzwertverhalten des Graphen für anhand des Funktionsterms von
anhand des Funktionsterms von 
Begründe das Grenzwertverhalten des Graphen für
(16 BE)
2.
Beschreibe unter Verwendung der Begriffe „Populationsgröße“ und „Wachstumgsgeschwindigkeit“ die Entwicklung der Käferpopulation. Deute dabei sowohl die Extrem- und Wendepunkte als auch den Grenzwert des Graphen aus Aufgabe 1.
(8 BE)
3.
Zeige, dass  mit
mit  eine Stammfunktion von
eine Stammfunktion von  ist. Berechne den Wert von
ist. Berechne den Wert von  und deute diesen im Sachzusammenhang.
und deute diesen im Sachzusammenhang.
(8 BE)
4.
Die Funktion  beschreibt die Entwicklung der Käferpopulation nur für die ersten 55 Jahre recht gut. Ab dem Zeitpunkt
beschreibt die Entwicklung der Käferpopulation nur für die ersten 55 Jahre recht gut. Ab dem Zeitpunkt  bleibt bei einer verbesserten Beschreibung die zu diesem Zeitpunkt erreichte Wachstumgsgeschwindigkeit konstant, sodass für
bleibt bei einer verbesserten Beschreibung die zu diesem Zeitpunkt erreichte Wachstumgsgeschwindigkeit konstant, sodass für  ein lineares Wachstum vorliegt.
ein lineares Wachstum vorliegt.
Berechne die momentane Wachstumsgeschwindigkeit bei und bestimme mit Hilfe der Funktionsgleichung, die ab diesem Punkt die Populationsgröße beschreibt, den voraussichtlichen Zeitpunkt des Aussterbens der Käferpopulation.
und bestimme mit Hilfe der Funktionsgleichung, die ab diesem Punkt die Populationsgröße beschreibt, den voraussichtlichen Zeitpunkt des Aussterbens der Käferpopulation.
Material
Berechne die momentane Wachstumsgeschwindigkeit bei
(8 BE)

1.
Extrempunkte bestimmen
1. Schritt: Notwendiges Kriterium für Extremstellen anwenden
Nullsetzen der ersten Ableitung  aus der Aufgabenstellung liefert:
2. Schritt: Zweite Ableitung von
aus der Aufgabenstellung liefert:
2. Schritt: Zweite Ableitung von  bestimmen
Mit Hilfe der Produkt- und Kettenregel folgt für die Ableitung von
bestimmen
Mit Hilfe der Produkt- und Kettenregel folgt für die Ableitung von 

 3. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Damit besitzt die Funktion
3. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Damit besitzt die Funktion  an der Stelle
an der Stelle  ein Maximum. Einsetzen von
ein Maximum. Einsetzen von  in
in  liefert:
liefert:




 Der Graph von
Der Graph von  besitzt einen Hochpunkt mit den Koordinaten
besitzt einen Hochpunkt mit den Koordinaten  Wendepunkte bestimmen
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
Nullsetzen von
Wendepunkte bestimmen
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
Nullsetzen von  liefert:
2. Schritt: Dritte Ableitung von
liefert:
2. Schritt: Dritte Ableitung von  bestimmen
Mit Hilfe der Produkt- und Kettenregel folgt für die Ableitung von
bestimmen
Mit Hilfe der Produkt- und Kettenregel folgt für die Ableitung von 

 3. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Damit besitzt die Funktion
3. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Damit besitzt die Funktion  an der Stelle
an der Stelle  eine Wendestelle. Einsetzen von
eine Wendestelle. Einsetzen von  in
in  liefert dann:
liefert dann:




 Der Graph von
Der Graph von  besitzt im Punkt mit den Koordinaten
besitzt im Punkt mit den Koordinaten  einen Wendepunkt.
Grenzwertverhalten begründen
Das Grenzwertverhalten der einzelnen Komponenten des Funktionsterms ist wie folgt:
einen Wendepunkt.
Grenzwertverhalten begründen
Das Grenzwertverhalten der einzelnen Komponenten des Funktionsterms ist wie folgt:
 besitzt lineares Wachstum und es gilt
besitzt lineares Wachstum und es gilt 

 besitzt exponentielles Wachstum und es gilt
besitzt exponentielles Wachstum und es gilt 

 Da exponentielles Wachstum stärker als lineares Wachstum ist, folgt für das Grenzwertverhalten des Funktionsterms von
Da exponentielles Wachstum stärker als lineares Wachstum ist, folgt für das Grenzwertverhalten des Funktionsterms von 



 .
.
2.
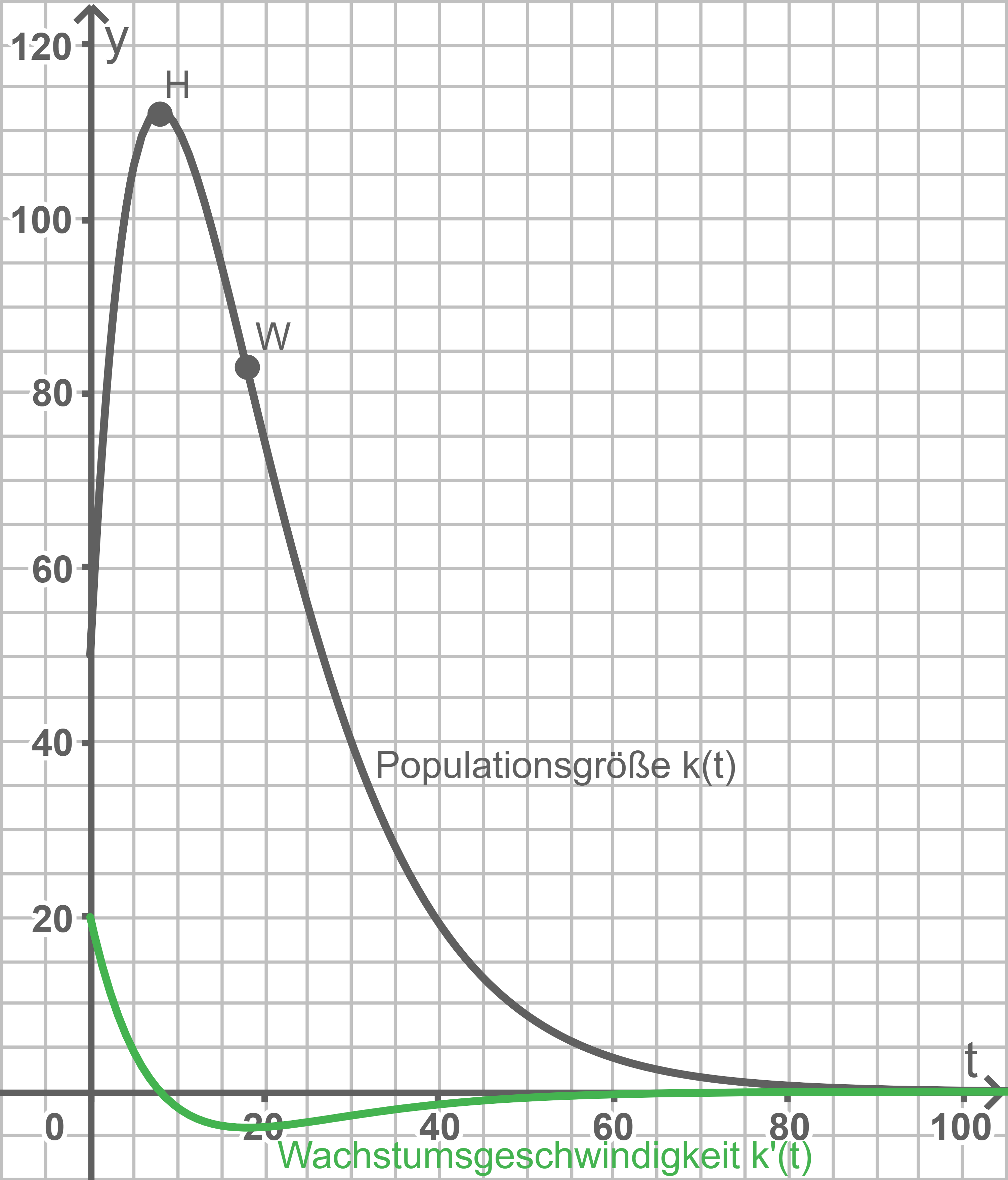
3.
Stammfunktion nachweisen
Mit Hilfe der Produkt- und Kettenregel folgt für die Ableitung von  Damit ist
Damit ist  eine Stammfunktion von
eine Stammfunktion von  .
Integral berechnen
Mit dem Hauptsatz der Integralrechnung folgt:
Integral im Sachzusammenhang deuten
Der Ausdruck
.
Integral berechnen
Mit dem Hauptsatz der Integralrechnung folgt:
Integral im Sachzusammenhang deuten
Der Ausdruck  gibt den durchschnittlichen Funktionswert des Graphen von
gibt den durchschnittlichen Funktionswert des Graphen von  zwischen
zwischen  und
und  an. Da eine Einheit der Funktionswerte
an. Da eine Einheit der Funktionswerte  Käfern entspricht, liefert
Käfern entspricht, liefert 
 die durchschnittliche Anzahl der Käfer zwischen Jahr
die durchschnittliche Anzahl der Käfer zwischen Jahr  und
und 
4.
Momentane Wachstumsgeschwindigkeit berechnen
Für die momentane Wachstumsgeschwindigkeit bei  folgt durch Einsetzen in
folgt durch Einsetzen in 





 Neue Funktionsgleichung bestimmen
Da ab der Stelle
Neue Funktionsgleichung bestimmen
Da ab der Stelle  ein lineares Wachstum für die Käferpopulation angenommen wird, beschreibt die Tangente
ein lineares Wachstum für die Käferpopulation angenommen wird, beschreibt die Tangente  mit allgemeiner Form
mit allgemeiner Form  an den Graphen von
an den Graphen von  an der Stelle
an der Stelle  den weiteren Verlauf.
den weiteren Verlauf.
Die Tangente die besitzt die Steigung , da dies die momentane Wachstumsgeschwindigkeit an der Stelle
, da dies die momentane Wachstumsgeschwindigkeit an der Stelle  ist. Somit gilt
ist. Somit gilt  .
.
Da die Tangente und die Funktion
und die Funktion  an der Stelle
an der Stelle  denselben
denselben  -Wert besitzen, folgt für
-Wert besitzen, folgt für  Voraussichtlichen Zeitpunkt des Aussterbens der Käferpopulation berechnen
Nullsetzen von
Voraussichtlichen Zeitpunkt des Aussterbens der Käferpopulation berechnen
Nullsetzen von  liefert:
Der voraussichtliche Zeitpunkt des Aussterbens der Käferpopulation ist also
liefert:
Der voraussichtliche Zeitpunkt des Aussterbens der Käferpopulation ist also  d.h. nach ca.
d.h. nach ca.  Jahren ist die Käferpopulation ausgestorben.
Jahren ist die Käferpopulation ausgestorben.
Die Tangente die besitzt die Steigung
Da die Tangente