B2 - Analysis
1
In einem Zoo wird ein Giraffenweibchen mit einer Körpergröße von  Metern geboren. Die Wachstumsphase des Giraffenweibchens beginnt unmittelbar mit der Geburt und endet nach sechs Jahren. Die Funktion
Metern geboren. Die Wachstumsphase des Giraffenweibchens beginnt unmittelbar mit der Geburt und endet nach sechs Jahren. Die Funktion  mit
mit  beschreibt im Intervall
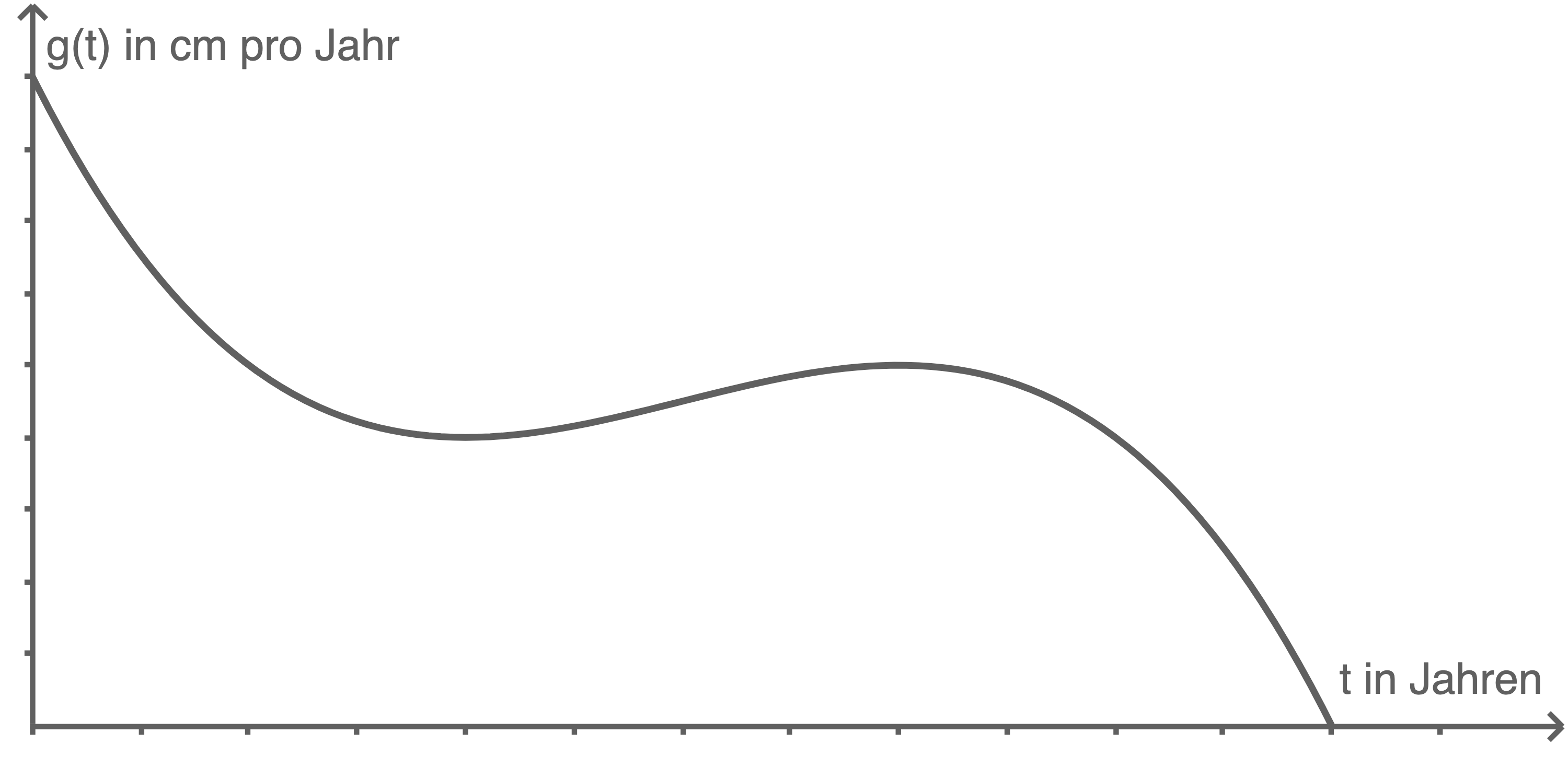
beschreibt im Intervall  in sehr guter Näherung die Wachstumsgeschwindigkeit des Giraffenweibchens (in
in sehr guter Näherung die Wachstumsgeschwindigkeit des Giraffenweibchens (in  pro Jahr) in Abhängigkeit von der Zeit
pro Jahr) in Abhängigkeit von der Zeit  (in Jahren nach der Geburt):
(in Jahren nach der Geburt):

1.1
Berechne  und
und  Erläutere die Bedeutung dieser beiden Werte im Sachzusammenhang und beschrifte die Achsen in der obigen Abbildung.
Erläutere die Bedeutung dieser beiden Werte im Sachzusammenhang und beschrifte die Achsen in der obigen Abbildung.
(6 BE)
1.2
Berechne zunächst ohne Beachtung des Sachkontexts die Koordinaten der Extrempunkte des Graphen von  Hinweis: Die Untersuchung der notwendigen Bedingungen ist ausreichend.
Hinweis: Die Untersuchung der notwendigen Bedingungen ist ausreichend.
(5 BE)
1.3
Erläutere nun, warum die in Aufgabenteil 1.2 für  berechneten Werte in Bezug auf die gesamte Wachstumsphase des Giraffenweibchens nicht diejenigen sind, an denen die Wachstumsgeschwindigkeit am größten bzw. am kleinsten ist.
berechneten Werte in Bezug auf die gesamte Wachstumsphase des Giraffenweibchens nicht diejenigen sind, an denen die Wachstumsgeschwindigkeit am größten bzw. am kleinsten ist.
(2 BE)
1.4
Berechne den Wert des Terms  Deute das Ergebnis im Sachzusammenhang.
Deute das Ergebnis im Sachzusammenhang.
(6 BE)
1.5
Für  stellt die Funktion
stellt die Funktion  die Größe des Giraffenweibchens (in
die Größe des Giraffenweibchens (in  ) in Abhängigkeit von der Zeit
) in Abhängigkeit von der Zeit  (in Jahren nach der Geburt) dar.
Gib eine Funktionsgleichung von
(in Jahren nach der Geburt) dar.
Gib eine Funktionsgleichung von  an und erläutere die Bedeutung des Wertes von
an und erläutere die Bedeutung des Wertes von  zum Zeitpunkt
zum Zeitpunkt 
(3 BE)
1.6
Begründe mit Hilfe des Verlaufs des Graphens von  dass der Graph der Funktion
dass der Graph der Funktion  im betrachteten Intervall monoton steigend ist, und erkläre, wie viele Wendepunkte der Graph von
im betrachteten Intervall monoton steigend ist, und erkläre, wie viele Wendepunkte der Graph von  besitzt.
besitzt.
(3 BE)
2
In einem anderen Zoo wird zur selben Zeit wie das Weibchen in Aufgabe 1 ein Giraffenmännchen mit einer Körpergröße von  Metern geboren. Das Weibchen wird
Metern geboren. Das Weibchen wird  Meter groß, das Männchen erreicht dagegen am Ende seiner sechsjährigen Wachstumsphase eine Größe von
Meter groß, das Männchen erreicht dagegen am Ende seiner sechsjährigen Wachstumsphase eine Größe von  Metern.
Es wird angenommen, dass die Wachstumsgeschwindigkeit des Männchens für
Metern.
Es wird angenommen, dass die Wachstumsgeschwindigkeit des Männchens für  durch eine Funktion der Schar
durch eine Funktion der Schar  mit
mit  beschrieben wird, wobei der Parameter
beschrieben wird, wobei der Parameter  eine positive reelle Zahl ist.
eine positive reelle Zahl ist.
2.1
Erkläre den Einfluss des Parameters  auf den Verlauf des Graphen von
auf den Verlauf des Graphen von  und beschreibe, was
und beschreibe, was  in Bezug auf das Wachstum des Giraffenmännchens bedeutet.
in Bezug auf das Wachstum des Giraffenmännchens bedeutet.
(3 BE)
2.2
Untersuche den Einfluss des Parameters  auf die jeweilige Lage des Wendepunktes der Graphen der Schar
auf die jeweilige Lage des Wendepunktes der Graphen der Schar 
(3 BE)
2.3
Erläutere die Ergebnisse der Berechnungen in Zeile  und
und  im Sachzusammenhang.
Zeige mit Hilfe des folgenden Kastens, dass
im Sachzusammenhang.
Zeige mit Hilfe des folgenden Kastens, dass  gelten muss.
Gib an, um wie viel Prozent die Wachstumsgeschwindigkeit des Männchens größer ist als die des Weibchens.
gelten muss.
Gib an, um wie viel Prozent die Wachstumsgeschwindigkeit des Männchens größer ist als die des Weibchens.


 Es gilt:
Es gilt: 
(5 BE)
3
Der Größenunterschied zwischen Männchen und Weibchen wird für  durch die Funktion
durch die Funktion  mit
mit 
 beschrieben. Der Graph von
beschrieben. Der Graph von  ist in der folgenden Abbildung abgebildet:
ist in der folgenden Abbildung abgebildet:
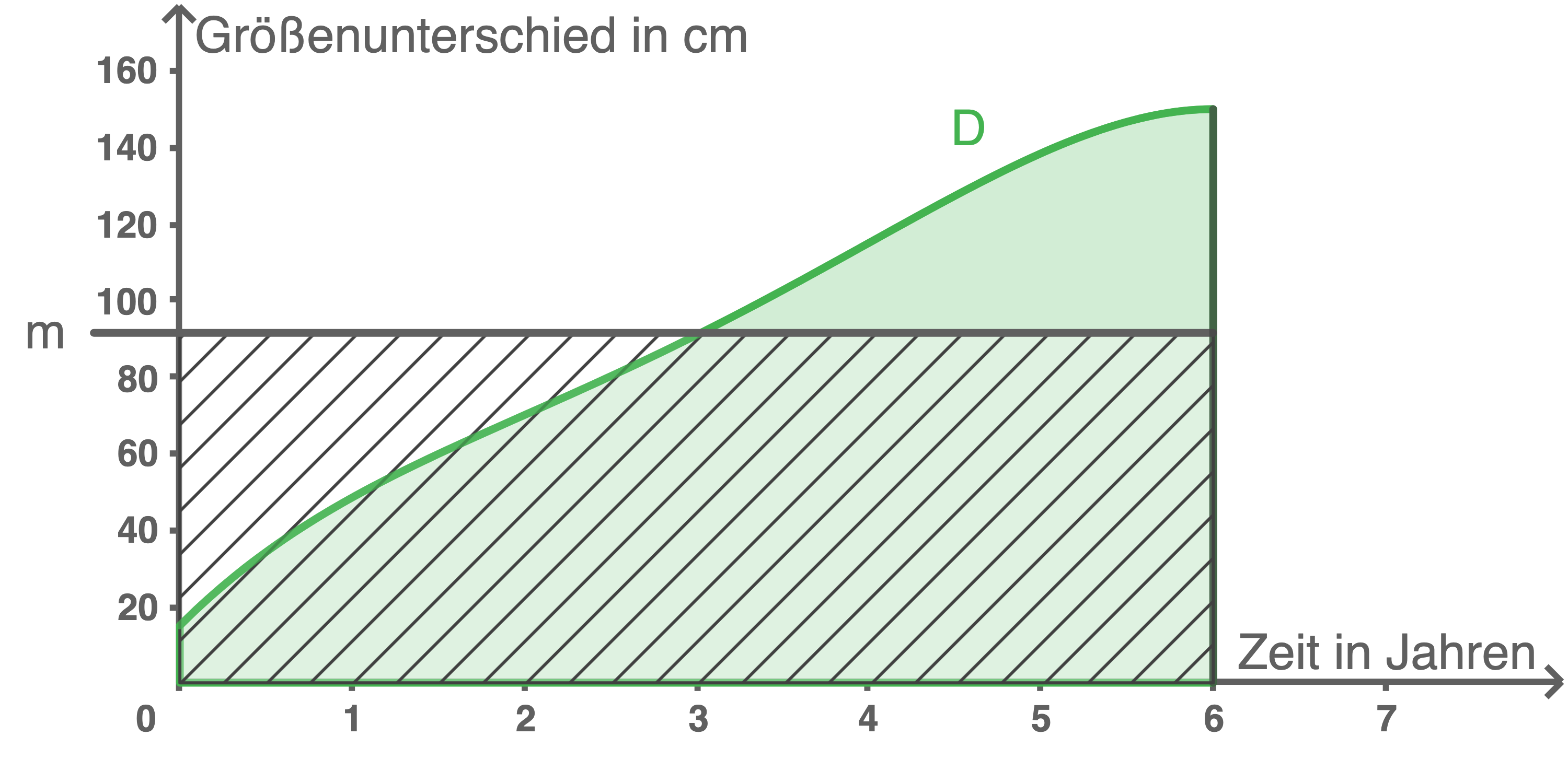 Die Fläche unter dem Graphen von
Die Fläche unter dem Graphen von  soll wie in der Abbildung dargestellt in ein flächeninhaltsgleiches Rechteck gleicher Breite umgewandelt werden.
Es gilt daher
soll wie in der Abbildung dargestellt in ein flächeninhaltsgleiches Rechteck gleicher Breite umgewandelt werden.
Es gilt daher  wobei
wobei  die Höhe des Rechtecks angibt.
Bestimme den Wert von
die Höhe des Rechtecks angibt.
Bestimme den Wert von  und deute das Ergebnis im Sachzusammenhang.
und deute das Ergebnis im Sachzusammenhang.

(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
1.1
Werte berechnen
![\(\begin{array}[t]{rll}
g(0)&=& -2,5 \cdot 0 + 22,5 \cdot 0 - 60 \cdot 0 +90& \\[5pt]
&=& 90& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/a9ec23a55c9bc550b5440cd7935776f59e3a7d26935f280acc9c564892c96ecd?color=5a5a5a) Sachzusammenhang erläutern
Sachzusammenhang erläutern
 : Während ihres Geburtsjahres wächst die Giraffe um
: Während ihres Geburtsjahres wächst die Giraffe um  .
.
 : Im Alter von sechs Jahren wächst die Giraffe nicht mehr.
Achsen beschriften
: Im Alter von sechs Jahren wächst die Giraffe nicht mehr.
Achsen beschriften
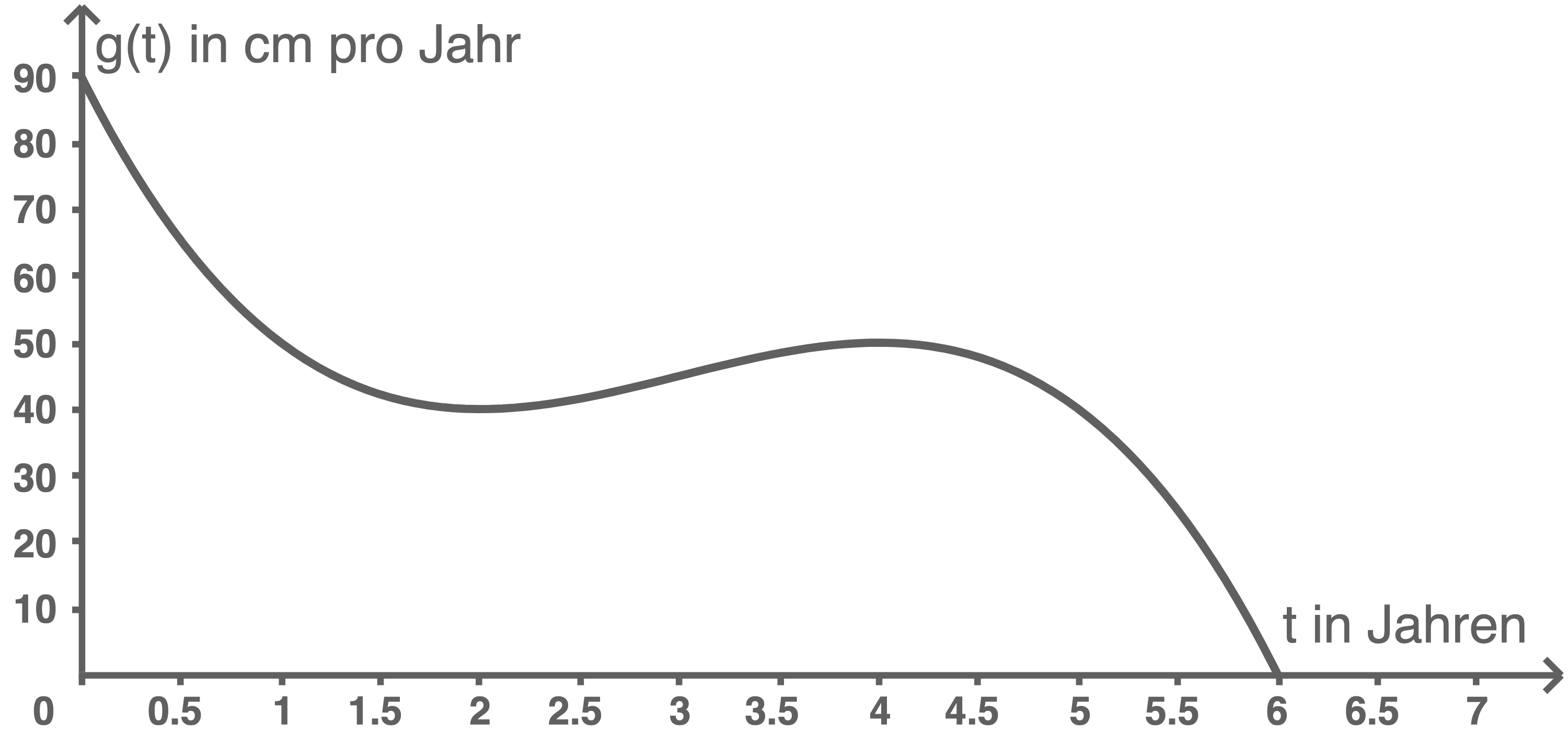

1.2
1. Schritt: Ableitung bestimmen
 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
g](https://mathjax.schullv.de/7ac7247f06480c4e095ac0a08a003aad8c77cefc7671f678a9bf4d6b4d3c1c75?color=5a5a5a) Mit der pq-Formel folgt:
Mit der pq-Formel folgt:
![\(\begin{array}[t]{rll}
t_{1;2}&=& - \dfrac{-6}{2} \pm \sqrt{\left(\dfrac{-6}{2} \right)^2 - 8}& \\[5pt]
t_{1;2}&=& 3\pm\sqrt{1}& \\[5pt]
t_1&=& 2& \\[5pt]
t_2&=& 4
\end{array}\)](https://mathjax.schullv.de/46b2ebb8821ff98a7067b0f498a016834b53a72bb5cc5967928662224f9e4bcc?color=5a5a5a) Laut Aufgabenstellung ist die Untersuchung der notwendigen Bedingung ausreichend und die hinreichende Bedingung muss somit nicht mehr geprüft werden.
3. Schritt:
Laut Aufgabenstellung ist die Untersuchung der notwendigen Bedingung ausreichend und die hinreichende Bedingung muss somit nicht mehr geprüft werden.
3. Schritt:  -Koordinaten berechnen
Somit sind die Koordinaten der Extrempunkte von
-Koordinaten berechnen
Somit sind die Koordinaten der Extrempunkte von  gegeben durch
gegeben durch  und
und 
1.3
Da die Wachstumsgeschwindigkeit des Giraffenweibchens nur im Intervall ![\([0 ; 6]\)](https://mathjax.schullv.de/955fce66cb9be6e04e2fd0be4db49e67d3973718de96e97d9aac29bfbf17c580?color=5a5a5a) abgebildet wird, können sich maximale bzw. minimale Werte auch auf den Rändern
abgebildet wird, können sich maximale bzw. minimale Werte auch auf den Rändern  und
und  des Intervalls befinden.
Dabei müssen diese keine Extremstelle sein.
In diesem Fall gilt:
des Intervalls befinden.
Dabei müssen diese keine Extremstelle sein.
In diesem Fall gilt:
 und
und  Damit sind die Extrempunkte von
Damit sind die Extrempunkte von  nicht die Punkte, an denen die Wachstumsgeschwindigkeit der Giraffe am kleinsten bzw. am größten ist.
nicht die Punkte, an denen die Wachstumsgeschwindigkeit der Giraffe am kleinsten bzw. am größten ist.
1.4
Der Term zeigt an, um wieviel  das Giraffenweibchen im Alter von ein bis vier Jahren durchschnittlich pro Jahr gewachsen ist.
das Giraffenweibchen im Alter von ein bis vier Jahren durchschnittlich pro Jahr gewachsen ist.
1.5
Funktionsgleichung angeben
Eine Funktionsgleichung von  ist somit beispielsweise
ist somit beispielsweise  Bedeutung erläutern
Der Wert von
Bedeutung erläutern
Der Wert von  zum Zeitpunkt
zum Zeitpunkt  gibt die Größe der Giraffe bei ihrer Geburt an. Laut Aufgabenstellung beträgt diese
gibt die Größe der Giraffe bei ihrer Geburt an. Laut Aufgabenstellung beträgt diese  Für die Funktionsgleichung folgt also:
Damit ergibt sich:
Für die Funktionsgleichung folgt also:
Damit ergibt sich:
1.6
Anhand des Graphen von  wird ersichtlich, dass
wird ersichtlich, dass  im Intervall
im Intervall ![\([0;6]\)](https://mathjax.schullv.de/acfdd226ea6f7581d0ec4c239b9512323dd93833ebec28e95f55c21030ec3b69?color=5a5a5a) nie negativ ist. Damit ist die Wachstumsgeschwindigkeit der Giraffe nie negativ, womit der Graph von
nie negativ ist. Damit ist die Wachstumsgeschwindigkeit der Giraffe nie negativ, womit der Graph von  monoton steigend ist.
Die Wendestellen von
monoton steigend ist.
Die Wendestellen von  entsprechen den Extremstellen von
entsprechen den Extremstellen von  . Somit hat der Graph von
. Somit hat der Graph von  zwei Wendepunkte im Intervall
zwei Wendepunkte im Intervall ![\([0;6]\)](https://mathjax.schullv.de/acfdd226ea6f7581d0ec4c239b9512323dd93833ebec28e95f55c21030ec3b69?color=5a5a5a) .
.
2
2.1
Da  als Faktor vor
als Faktor vor  steht, handelt es sich bei der Funktionenschar
steht, handelt es sich bei der Funktionenschar  um eine Streckung bzw. Stauchung von
um eine Streckung bzw. Stauchung von  entlang der
entlang der  -Achse. Wählt man dabei
-Achse. Wählt man dabei  dann wird
dann wird  entlang der
entlang der  -Achse gestreckt.
Im Sachzusammenhang bedeutet also
-Achse gestreckt.
Im Sachzusammenhang bedeutet also  eine höhere Wachstumsgeschwindigkeit des Giraffenmännchens im Vergleich zu der des Weibchens.
eine höhere Wachstumsgeschwindigkeit des Giraffenmännchens im Vergleich zu der des Weibchens.
2.2
1. Schritt: Ableitungen bestimmen
![\(\begin{array}[t]{rll}
f_{a}](https://mathjax.schullv.de/22a1f20e759740fd5daccf2a7172a96f1ce9c6b7d1bdd6f0f2d57ec4de4e4344?color=5a5a5a)
![\(\begin{array}[t]{rll}
f_{a}](https://mathjax.schullv.de/08db95a605127145a0c41ea8f83ec378d757042d30f56276d0b0b1ed8dcd1d70?color=5a5a5a) 2. Schritt: Notwendige Bedingung für Wendestellen anwenden
2. Schritt: Notwendige Bedingung für Wendestellen anwenden
![\(\begin{array}[t]{rll}
f_{a}](https://mathjax.schullv.de/61010a443ec8f24f9655f1e06c41ab2288a1a0c3a959f169abc2372b2e51c405?color=5a5a5a) Aus der Aufgabenstellung geht bereits hervor, dass ein Wendepunkt existiert. Die hinreichende Bedingung für Wendestellen muss somit nicht mehr geprüft werden.
3. Schritt:
Aus der Aufgabenstellung geht bereits hervor, dass ein Wendepunkt existiert. Die hinreichende Bedingung für Wendestellen muss somit nicht mehr geprüft werden.
3. Schritt:  -Koordinate bestimmen
Die Koordinaten des Wendepunktes sind somit gegeben durch
-Koordinate bestimmen
Die Koordinaten des Wendepunktes sind somit gegeben durch  .
Folglich hat der Parameter
.
Folglich hat der Parameter  Einfluss auf die
Einfluss auf die  -Koordinate des Wendepunktes, jedoch nicht auf die
-Koordinate des Wendepunktes, jedoch nicht auf die  -Koordinate.
-Koordinate.
2.3
Ergebnisse erläutern
 Anzahl an
Anzahl an  , die ein Giraffenmännchen nach Geburt noch wächst.
, die ein Giraffenmännchen nach Geburt noch wächst.
 Anzahl an
Anzahl an  , die ein Giraffenweibchen nach Geburt noch wächst.
Wachstumsgeschwindigkeiten vergleichen
Nach
, die ein Giraffenweibchen nach Geburt noch wächst.
Wachstumsgeschwindigkeiten vergleichen
Nach  gilt:
Somit gilt
gilt:
Somit gilt  .
Daraus folgt, dass die Wachstumsgeschwindigkeit des Männchens um
.
Daraus folgt, dass die Wachstumsgeschwindigkeit des Männchens um  größer ist als die des Weibchens.
größer ist als die des Weibchens.
3
Wert von  bestimmen
Es gilt:
Ergebnis deuten
Im Sachzusammenhang bedeutet das Ergebnis
bestimmen
Es gilt:
Ergebnis deuten
Im Sachzusammenhang bedeutet das Ergebnis  , dass bis zum Alter von sechs Jahren das Giraffenmännchen durchschnittlich
, dass bis zum Alter von sechs Jahren das Giraffenmännchen durchschnittlich  größer ist als das Giraffenweibchen.
größer ist als das Giraffenweibchen.