B1 - Analysis

Die Geschwindigkeit eines Läufers auf einem Laufband soll für $t \geq 0$ mithilfe der Funktion $g$ mit $g ( t )=0,5 t ^4-2 t ^3+2 t ^2$ beschrieben werden ( $t$ : Zeit in Minuten, $g(t)$ : Geschwindigkeit in Kilometern pro Minute). Der Graph von $g$ ist ausschnittsweise in Material 1 dargestellt.

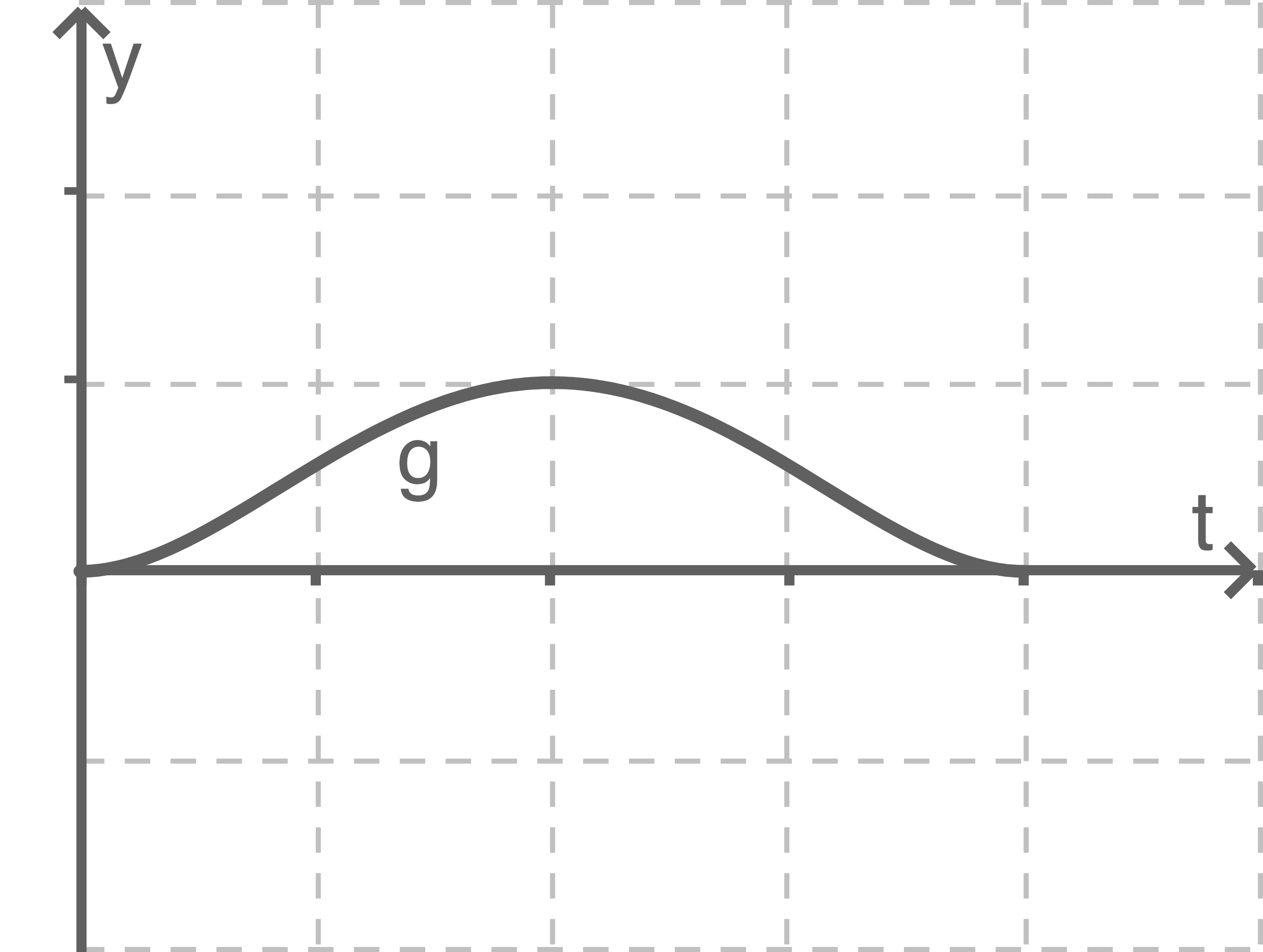
hessen mathe abi gk wtr 2022 teil b1 abbildung 1

Material 1
Graph der Funktion $g$

1.1

Berechne die Nullstellen von $g$ sowie die Art und die Lage der Extrempunkte des Graphen von $g$ .
Beschrifte die Koordinatenachsen in Material 1 mit einer geeigneten Skala.

(9 BE)

1.2

Erläutere die Bedeutung des Hochpunktes sowie die Bedeutung des Terms $\dfrac{ g (1)- g (0,5)}{1-0,5}$ jeweils im Sachzusammenhang.

(4 BE)

1.3

Skizziere den Verlauf des Graphen der Ableitungsfunktion $g ^{\prime}$ in das Koordinatensystem in Material $1$ .
Erläutere zudem die Bedeutung von $g^{\prime}$ im Sachzusammenhang.

(4 BE)

1.4

Berechne die Länge des Weges in Metern, den der Läufer in den ersten zwei Minuten auf dem Laufband zurücklegt.

(4 BE)

Gegeben ist die Funktionenschar $f _{ a }$ mit $f_{a}(t)=0,5t^4-2t^3+(2-0,5 a )t^2+$ $at$ $($ mit $a \geq 0)$ .
Die Graphen einiger Funktionen der Schar sind in Material 2 dargestellt, darunter auch der Graph der zur Schar gehörenden Funktion $g$ aus Aufgabe 1 mit $g=f_0$ .
Die Hochpunkte der Funktionenschar haben die Koordinaten $H_{a}(1 \mid 0,5 a +0,5)$ .

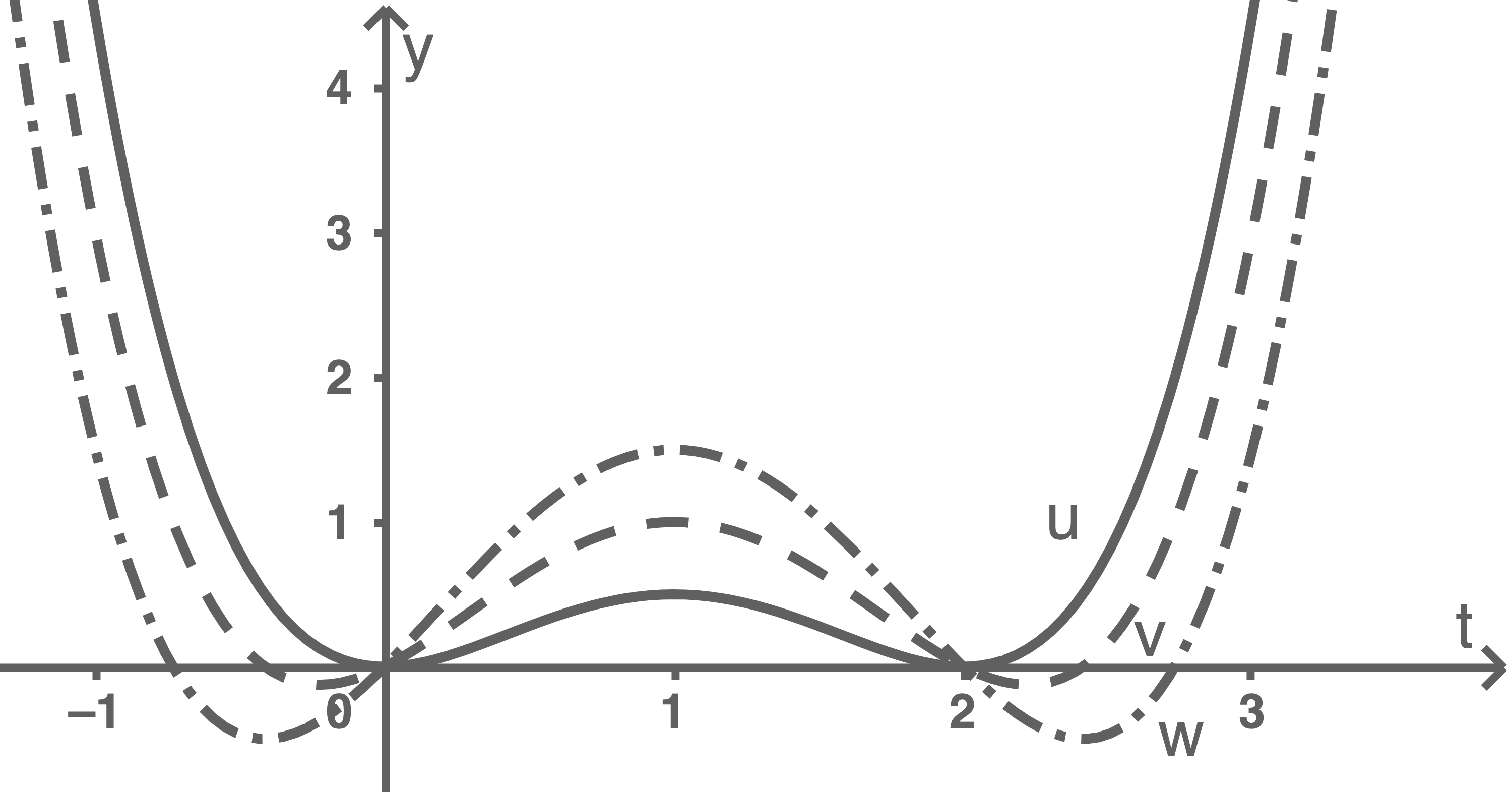
hessen mathe abi gk wtr 2022 teil b1 abbildung 2

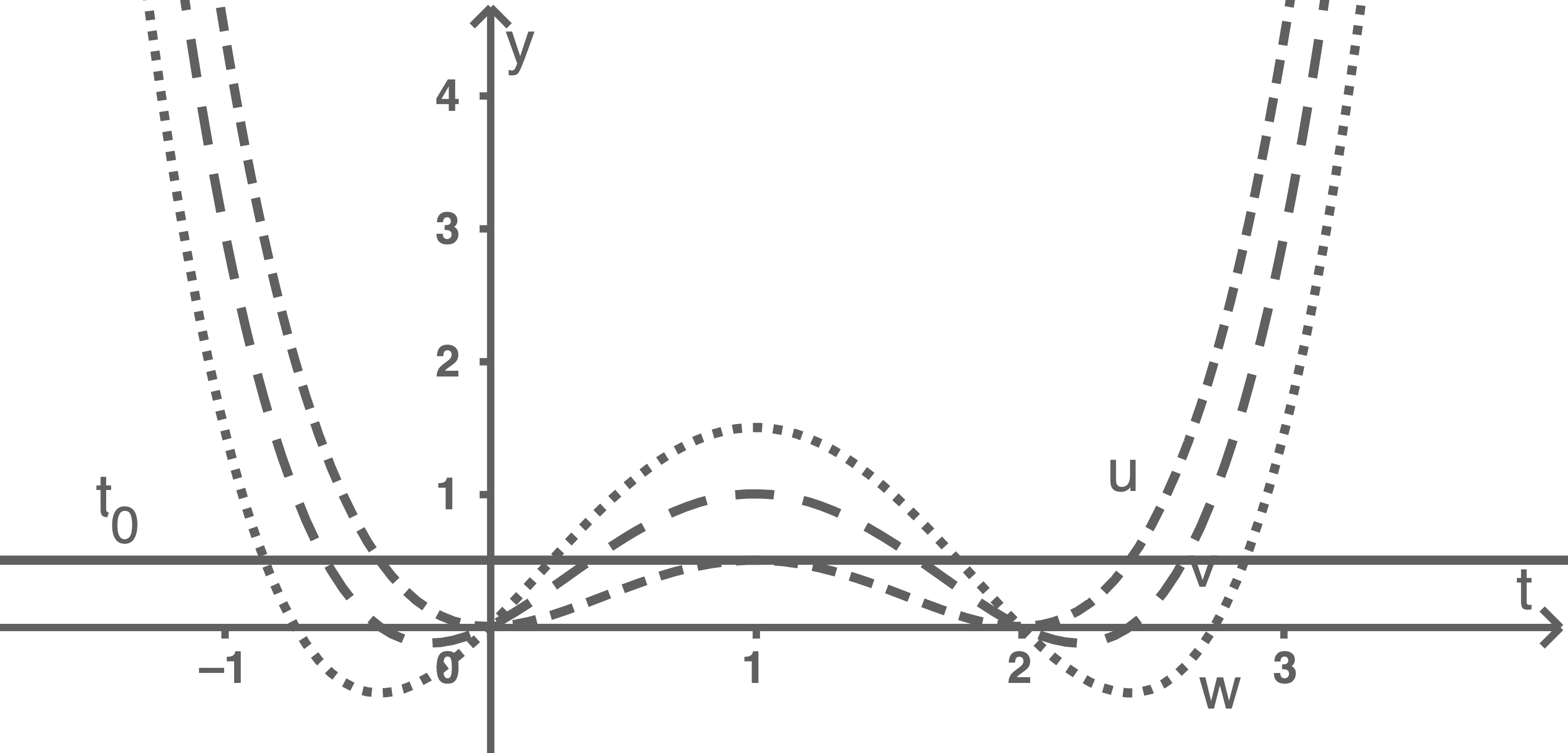
Material 2
Graphen der Funktion $f_a$

2.1

Ordne die Parameter $a=1$ und $a=2$ begründet jeweils einem der Graphen $u , v$ und $w$ in Material 2 zu.
Beschreibe anhand von Material 2 die Bedeutung des Parameters $a$ für die Lage der Hochpunkte.

(6 BE)

2.2

Skizziere in Material 2 die Tangente an den Hochpunkt des Graphen von $f_0$ .
Beschreibe, wie man den Inhalt der Fläche bestimmen kann, die zwischen dieser Tangente und dem Graphen von $f_0$ eingeschlossen ist.

(4 BE)

2.3

Zeige rechnerisch, dass für die Wendestellen von $f_a$ gilt: $t_{1/2}=1 \pm \sqrt{1-\dfrac{4-a}{6}}$
Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.
Bestimme den Wert des Parameters $a$ , für den die beiden Nullstellen bei $t=0$ und $t=2$ gleichzeitig auch die Wendestellen von $f_{a}$ sind.

(5 BE)

2.4

Nachfolgend sind einige Termumformungen angegeben, mithilfe derer der Funktionsterm von $f_a$ als Differenz des Funktionsterms von $f_0$ und des Terms einer Funktionenschar $p_a$ dargestellt werden kann.
Erläutere die von Zeile $\,\text {II}$ zu Zeile $\,\text {III}$ durchgeführten Umformungen.
Begründe anhand des Funktionsterms von $p_a$ in Zeile $\,\text {III}$ die Lage der Nullstellen von $p_a$ .

Termumformungen anzeigen

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Nullstellen berechnen

$\begin{array}[t]{rll} g(t)&=& 0 & \\[5pt] 0,5 t ^4-2 t ^3+2 t ^2&=& 0 & \\[5pt] (0,5 t ^2-2 t +2) \cdot t ^2&=& 0 & \\[5pt] \end{array}$

Mit dem Satz vom Nullprodukt folgt sofort: $t_1=0$

Anwenden der $pq$ -Formel:

Durch Multiplizieren mit dem Faktor $2$ ergeben sich $p=-4$ und $q=4.$

$\begin{array}[t]{rll} t_{2}&=& -\left(\dfrac{-4}{2}\right) \pm \sqrt{\left(\dfrac{-4}{2}\right)^2-4} &\\[5pt] &=& 2 \pm \sqrt{0} & \\[5pt] &=& 2 & \\[5pt] \end{array}$

Die Nullstellen von $g$ befinden sich somit bei $t_1=0$ und $t_2=2.$

Extrempunkte berechnen

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} g$

Mit dem Satz vom Nullprodukt folgt sofort: $t_3=0$

Anwenden der $pq$ -Formel:

Durch Dividieren mit dem Faktor $2$ ergeben sich $p=-3$ und $q=2.$

$\begin{array}[t]{rll} t_{4,5}&=& -\left(\dfrac{-3}{2}\right) \pm \sqrt{\left(\dfrac{-3}{2}\right)^2-2} &\\[5pt] &=& 1,5 \pm \sqrt{0,25} & \\[5pt] &=& 1,5 \pm 0,5 & \\[5pt] \end{array}$

Es folgt: $t_4=1$ und $t_5=2$

2. Schritt: Hinreichende Bedingung für Extremstellen prüfen

$\(g$

3. Schritt: $y$ -Koordinaten bestimmen

Da bereits gezeigt wurde, dass $t=0$ und $t=2$ Nullstellen sind, ergeben sich die Tiefpunkte $T_1(0\mid 0)$ und $T_2(2 \mid 0).$

$g(1)=0,5 \cdot 1 ^4-2 \cdot 1 ^3+2 \cdot 1 ^2=0,5$

Der Punkt $H(1 \mid 0,5)$ ist folglich Hochpunkt des Graphen von $g.$

Koordinatenachsen beschriften

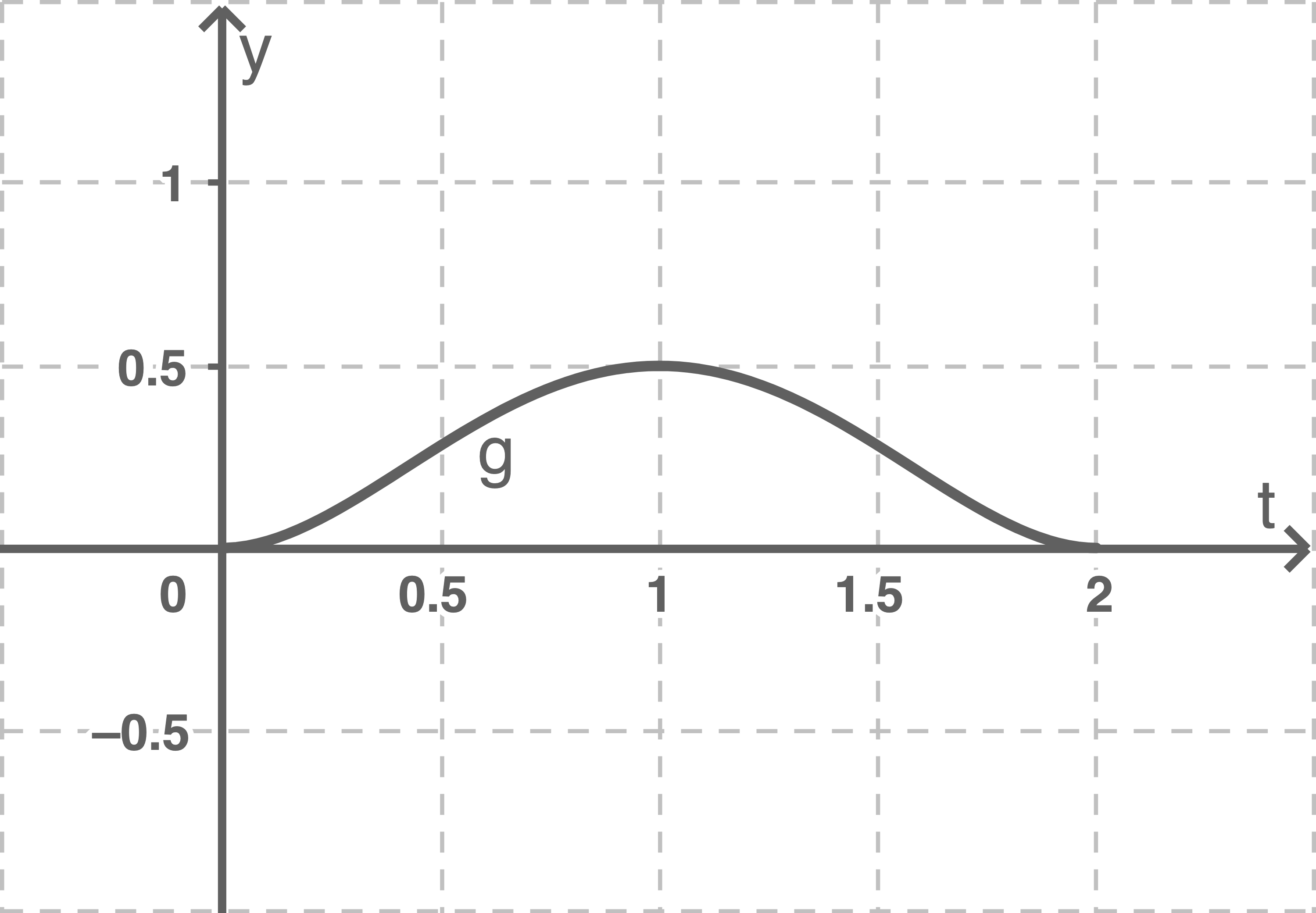
Lauf Geschwindigkeit Kilometer pro Minute Hessen Abi

1.2

Bedeutung des Hochpunkts

Der Hochpunkt beschreibt den Zeitpunkt, zu welchem der Läufer am schnellsten ist. Nach einer Minute läuft er mit einer Höchstgeschwindigkeit von $0,5 \dfrac{\text{km}}{\text{min}}.$

Bedeutung des Terms

Der Term beschreibt die mittlere/durchschnittliche Geschwindigkeitsänderung des Läufers zwischen der ersten halben Minute und der ersten Minute.

1.3

Verlauf des Graphen der Ableitungsfunktion $\(g$

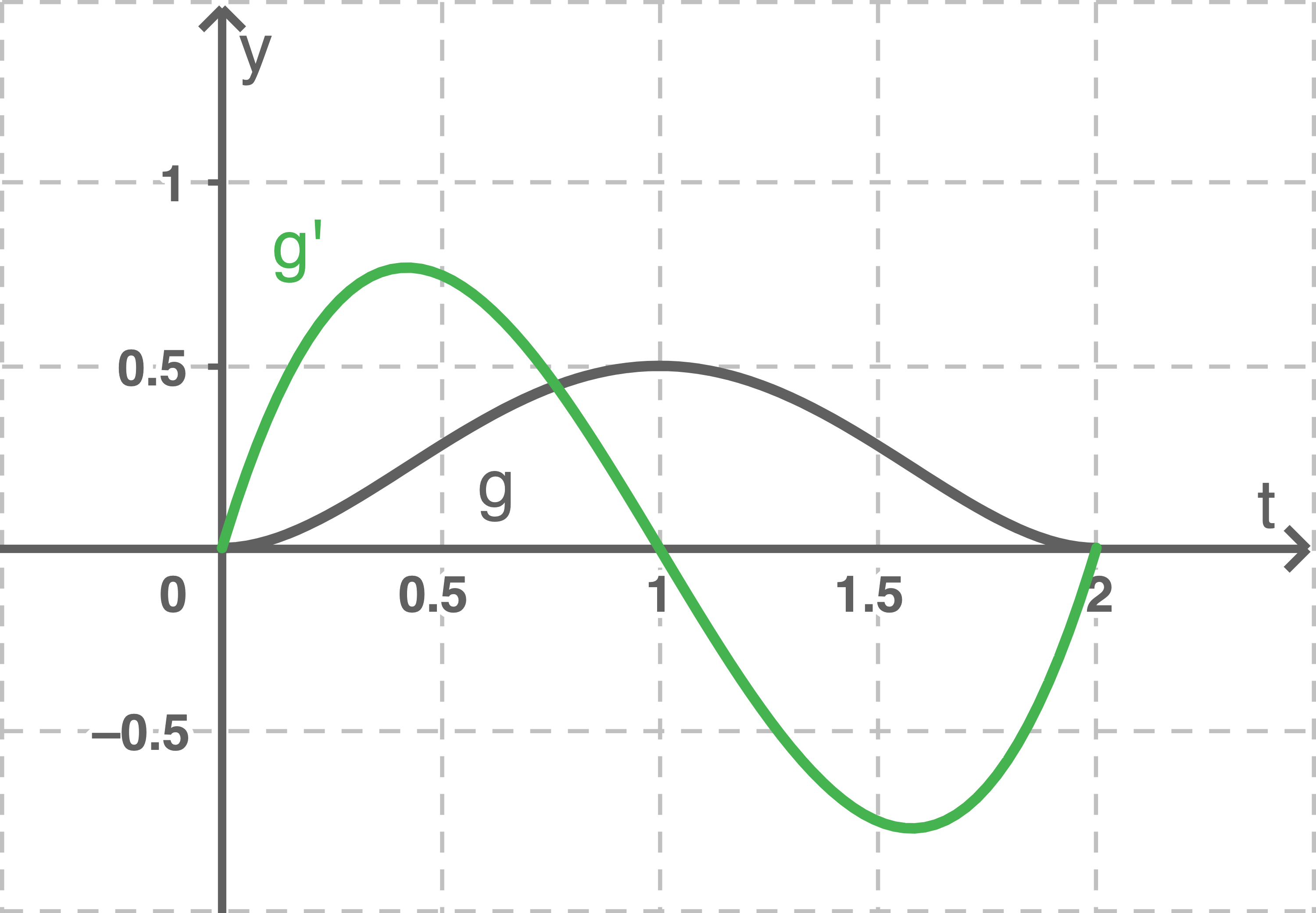Bedeutung von $\(g$

Die Ableitungsfunktion $\(g$ beschreibt die Änderung der Geschwindigkeit. Die Extrempunkte von $\(g$ entsprechen somit den Zeitpunkten, zu welchen die Geschwindigkeit des Läufers am stärksten ab- beziehungsweise zunimmt.

1.4

Rechenweg anzeigen

$\displaystyle\int_{0}^{2}g(t)\;\mathrm dt \approx 0,53 \;[\,\text{km}]$

Der Läufer legt somit in den ersten 2 Minuten einen Weg der Länge $0,53 \,\text{km}$ zurück.

2.1

Hochpunkte zuordnen

Da $H_a(1 \mid 0,5\cdot a +0,5)$ gilt, können die Koordinaten der Hochpunkte bestimmt werden.

Für den Parameter $a=1$ folgen die Koordinaten mit $H_1(1 \mid 1).$

Der Parameter $a=1$ lässt sich somit dem Graphen $v$ zuordnen.

Für $a=2$ folgen die Koordinaten mit $H_2(1 \mid 1,5)$ und deshalb handelt es sich in diesem Fall um den Graphen $w.$

Bedeutung des Parameters $a$

Aus dem Material 2 kann abgelesen werden, dass der Parameter $a$ den Hochpunkt in $y$ -Richtung verschiebt.

Je größer der Wert von $a$ , desto größer auch der Abstand des Hochpunkts zur $x$ -Achse.

Die $x$ -Koordinaten der Hochpunkte bleiben unabhängig vom Parameter $a$ unverändert.

2.2

Skizze der Tangente $t_0$ an den Hochpunkt von $f_0$

Tangente Graph Funktionenschar Hessen Abi

Inhalt der Fläche bestimmen, die von der Tangente und dem Graphen von $f_0$ eingeschlossen wird

Schnittstellen $S_1$ und $S_2$ der Tangente mit dem Graphen von $f_0$ durch Gleichsetzen der beiden Funktionen bestimmen
Differenzfunktion $d(t)= y-f_0(t)$ bilden
Integral aufstellen: $\displaystyle\int_{S_1}^{S_2}d(t) \;\mathrm dt$

2.3

$\(f_a$

1. Schritt: Notwendige Bedingung für Wendestellen anwenden

$\(\begin{array}[t]{rll} f_a$

Anwenden der $pq$ -Formel:

Rechenweg anzeigen

$t_{1/2} =1 \pm \sqrt{1-\dfrac{4-a}{6} }$

Wert des Parameters $a$ bestimmen

Für $t_1=0$ folgt:

Rechenweg anzeigen

$4&=& a$

Kontrolle durch Einsetzen von $a=4$ in $t_2:$

$\begin{array}[t]{rll} t_2&=& 1 + \sqrt{1-\dfrac{4-4}{6} }& \\[5pt] &=& 2 \end{array}$

Für den Wert des Parameters $a=4$ sind folglich die beiden Nullstellen bei $t=0$ und $t=2$ gleichzeitig auch Wendestellen von $f_a.$

2.4

Umformungen erläutern

Von Zeile $(\text{II})$ zu Zeile $(\text{III})$ wird in beiden Teilgleichungen jeweils die Variable $t$ mit einem möglichst hohen Exponenten ausgeklammert.

In der vorderen Teilgleichung, dem Term von $f_0(t),$ wird nach dem Ausklammern von $t^2$ zusätzlich die zweite binomische Formel angewandt.

Lage der Nullstellen begründen

Durch diese Umformung lässt sich der Satz vom Nullprodukt auf die beiden Teilgleichungen anwenden.

Für $a=0$ gilt $p_0(t)=0.$

Für $a \gt 0$ und durch die Anwendung des Satzes vom Nullprodukt auf den Funktionsterm von $p_a$ in Zeile $(\text{III})$ ergeben sich die Nullstellen $t=0$ und $t=2.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?