A2 - Analysis
Während einer schulischen Projektwoche werden Modelle von Heißluftballons aus dünnem Papier gefertigt. Um das Flugverhalten der Heißluftballons zu untersuchen, werden die Ballons mit heißer Luft gefüllt und dann losgelassen (Abbildung 1).

Abbildung 1
1
Eine Ballonhülle (Abbildung 2) besteht aus sechs zueinander kongruenten, miteinander verklebten Teilen. Ein Ballonhüllenteil ist in Abbildung 3 abgebildet. Es ist achsensymmetrisch zur  -Achse und
-Achse und  lang. Seine obere Randkurve wird für
lang. Seine obere Randkurve wird für  durch den Graphen der Funktion
durch den Graphen der Funktion  mit
mit  beschrieben (alle Angaben in
beschrieben (alle Angaben in  ). Der weitere Verlauf des Graphen von
). Der weitere Verlauf des Graphen von  ist für
ist für  gestrichelt dargestellt.
gestrichelt dargestellt.
Für wird die obere Randkurve durch die Tangente
wird die obere Randkurve durch die Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  beschrieben.
beschrieben.

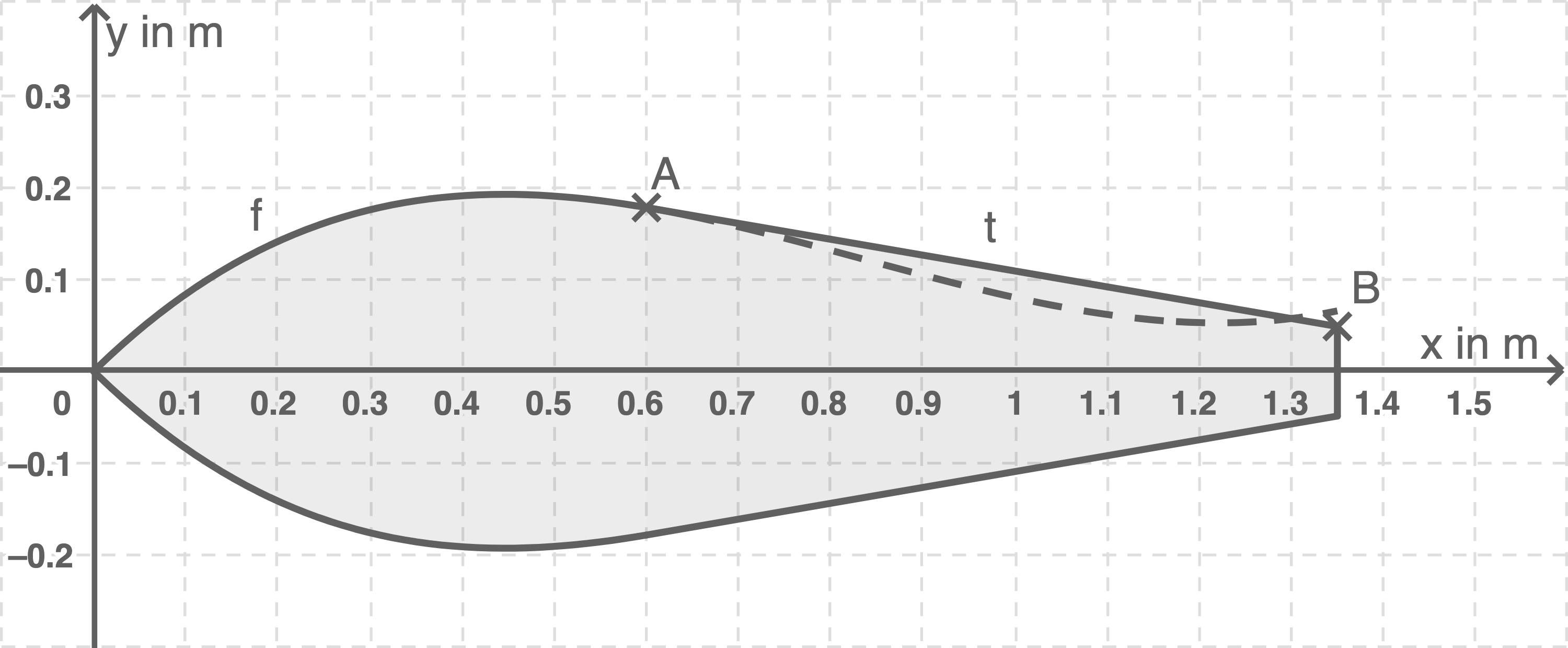
Für

Abbildung 2

Abbildung 3
1.1
Berechne die maximale Breite eines Ballonhüllenteils.
Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.
Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.
(6 BE)
1.2
Berechne die Funktionsgleichung der Tangente 
Verwende im Folgenden für die Tangente
(5 BE)
1.3
Berechne den Flächeninhalt  eines Ballonhüllenteils.
eines Ballonhüllenteils.
[Zur Kontrolle: ]
]
[Zur Kontrolle:
(8 BE)
1.4
Die gesamte Ballonhülle soll insgesamt höchstens  wiegen. Zum Verkleben der sechs Ballonhüllenteile werden für die gesamte Ballonhülle insgesamt
wiegen. Zum Verkleben der sechs Ballonhüllenteile werden für die gesamte Ballonhülle insgesamt  Klebstoff benötigt.
Klebstoff benötigt.
Berechne, wie viel Gramm pro das Papier höchstens wiegen darf.
das Papier höchstens wiegen darf.
Berechne, wie viel Gramm pro
(5 BE)
2
Es werden drei verschiedene Ballonfahrten durchgeführt. Der Ballon wird jeweils zum Zeitpunkt  in einem Meter Höhe über dem ebenen Boden losgelassen. Die Funktionen
in einem Meter Höhe über dem ebenen Boden losgelassen. Die Funktionen 
 und
und  geben jeweils an, in welcher Höhe (in
geben jeweils an, in welcher Höhe (in  ) über dem Boden sich der Ballon zur Zeit
) über dem Boden sich der Ballon zur Zeit  (in Sekunden nach Beginn der Messung) befindet. Mithilfe einer Filmaufnahme wird untersucht, mit welcher Geschwindigkeit
(in Sekunden nach Beginn der Messung) befindet. Mithilfe einer Filmaufnahme wird untersucht, mit welcher Geschwindigkeit 
 der Ballon zunächst aufsteigt und anschließend wieder absinkt. Zur Modellierung werden die drei Funktionen
der Ballon zunächst aufsteigt und anschließend wieder absinkt. Zur Modellierung werden die drei Funktionen 
 und
und  verwendet. Die Funktionen
verwendet. Die Funktionen 
 und
und  sind die jeweiligen ersten Ableitungen der Funktionen
sind die jeweiligen ersten Ableitungen der Funktionen 
 und
und 
2.1
In Abbildung 4 ist der Graph von  in Abhängigkeit von der Zeit
in Abhängigkeit von der Zeit  für
für  dargestellt.
Erläutere anhand der Eigenschaften des Graphen von
dargestellt.
Erläutere anhand der Eigenschaften des Graphen von  den Verlauf des zugehörigen Graphen von
den Verlauf des zugehörigen Graphen von  Gehe dabei auf das Monotonieverhalten und mögliche Extremwerte des Graphen von
Gehe dabei auf das Monotonieverhalten und mögliche Extremwerte des Graphen von  innerhalb des betrachteten Intervalls ein.
innerhalb des betrachteten Intervalls ein.
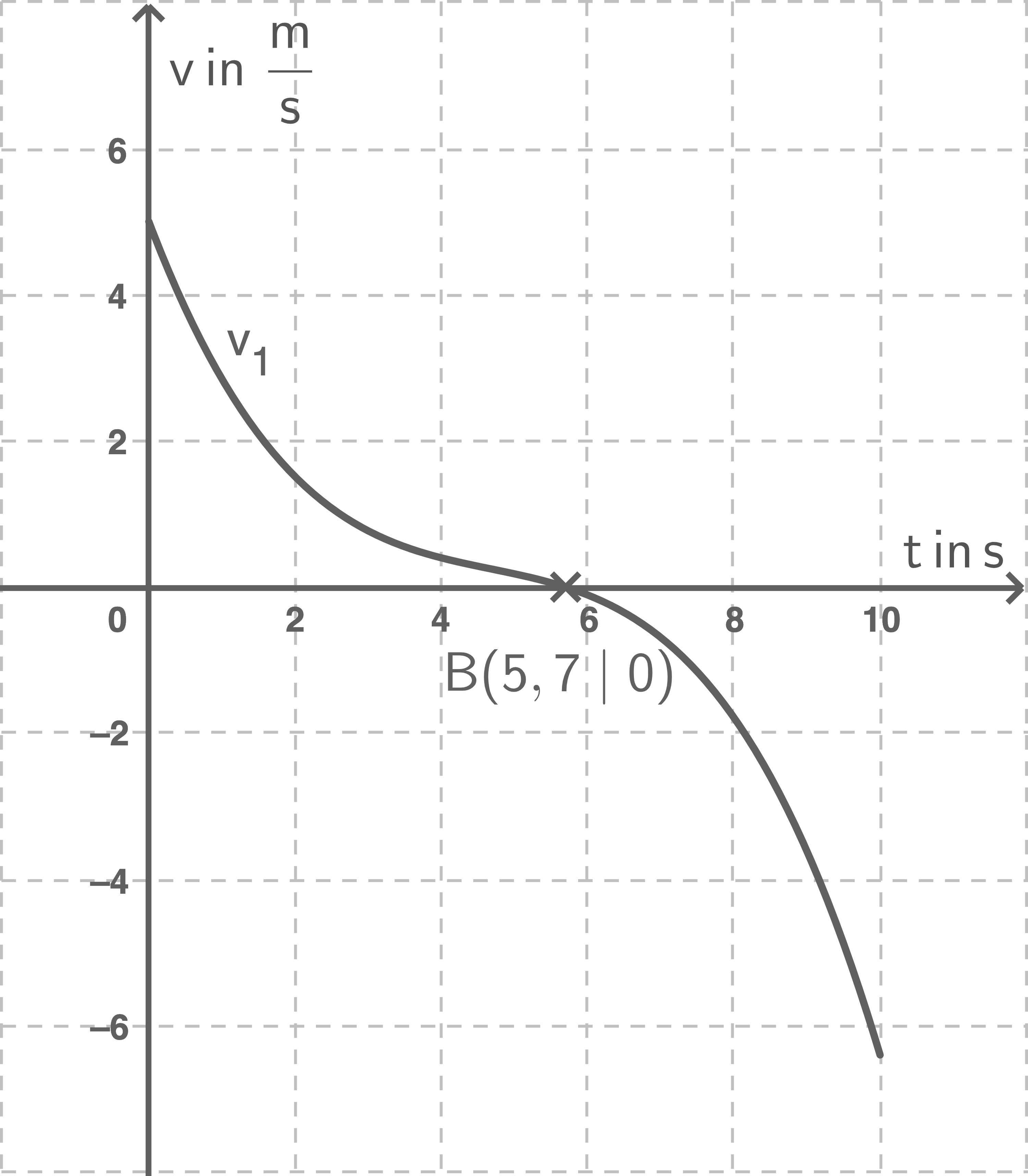
Abbildung 4
(7 BE)
2.2
In Abbildung 5 ist der Graph der Funktion  mit
mit
 für
für  dargestellt.
Bestimme die Höhe des Ballons über dem Boden zum Zeitpunkt
dargestellt.
Bestimme die Höhe des Ballons über dem Boden zum Zeitpunkt 
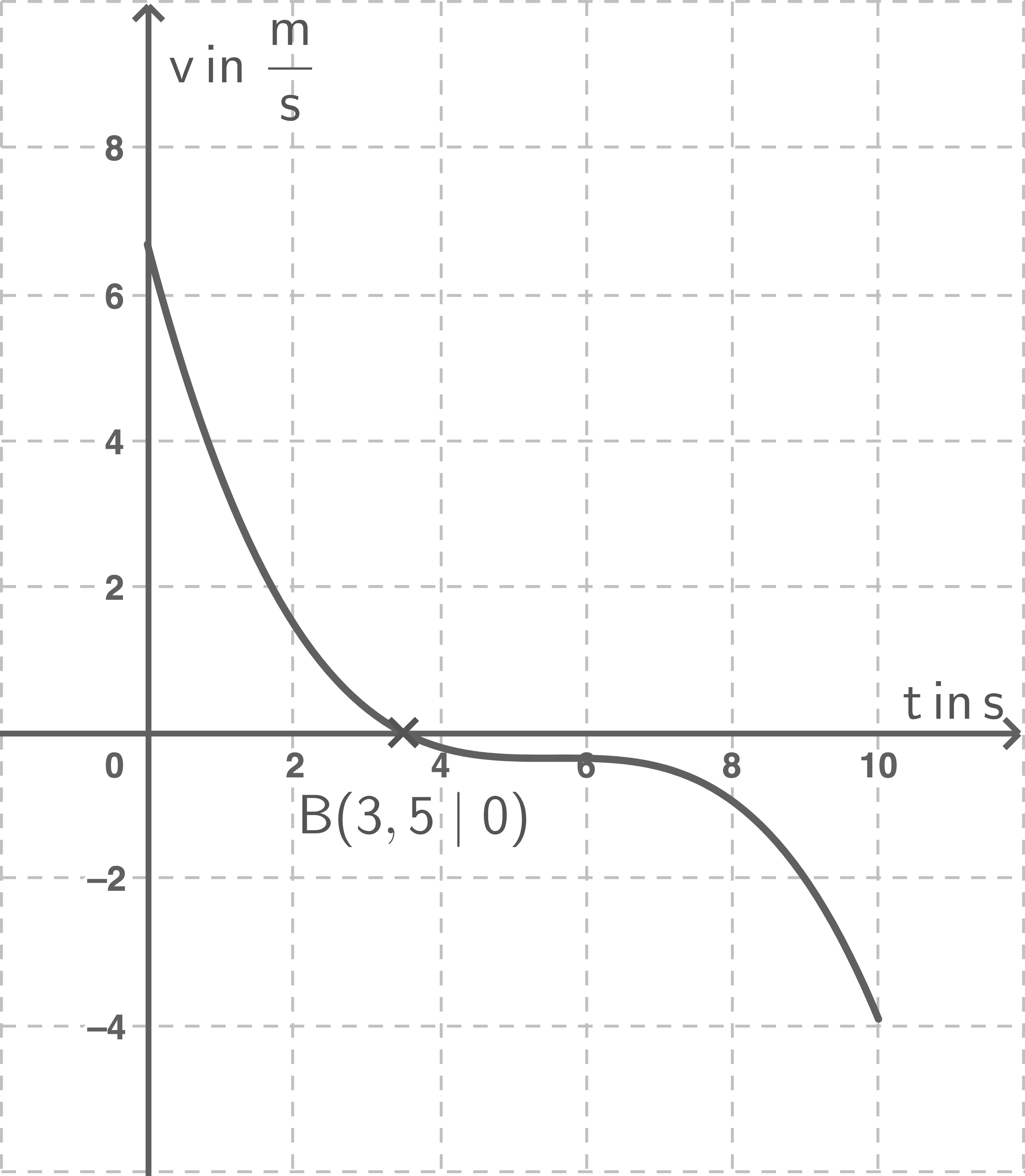
Abbildung 5
(4 BE)
2.3
Für die dritte Ballonfahrt gelten die folgenden Bedingungen:

 Beschreibe jeweils die Bedeutung der Bedingungen (1) und (2) im Sachzusammenhang.
Beschreibe jeweils die Bedeutung der Bedingungen (1) und (2) im Sachzusammenhang.
Erläutere, was sich aus den Bedingungen (1) und (2) für die Höhe des Ballons zum Zeitpunkt folgern lässt.
folgern lässt.
(1)
(2)
Erläutere, was sich aus den Bedingungen (1) und (2) für die Höhe des Ballons zum Zeitpunkt
(5 BE)
1.1
1. Schritt: Ableitung bilden
2. Schritt: Notwendiges Kriterium für Extremstellen anwenden
Die einzige Lösung im betrachteten Bereich ist  Da laut Aufgabenstellung die Überprüfung des hinreichenden Kriteriums nicht notwendig ist, befindet sich die breiteste Stelle des Ballonhüllenteils im Modell somit an der Stelle
Da laut Aufgabenstellung die Überprüfung des hinreichenden Kriteriums nicht notwendig ist, befindet sich die breiteste Stelle des Ballonhüllenteils im Modell somit an der Stelle  3. Schritt: Maximale Breite berechnen
3. Schritt: Maximale Breite berechnen



![\( \approx 0,38 \;\text{[m]}\)](https://mathjax.schullv.de/bf4f13aaa0d5b403cb08041a828b6abfe1f41c6c9b345ef4f5bde7632c4d229e?color=5a5a5a)
1.2
Für eine Tangente gilt allgemein  Die Steigung der Tangente
Die Steigung der Tangente  entspricht der Steigung des Graphen von
entspricht der Steigung des Graphen von  im Punkt
im Punkt 



 Für die
Für die  -Koordinate von
-Koordinate von  gilt:
gilt:



 Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  in
in  liefert:
Die Funktionsgleichung der Tangente lautet somit:
liefert:
Die Funktionsgleichung der Tangente lautet somit:

1.3
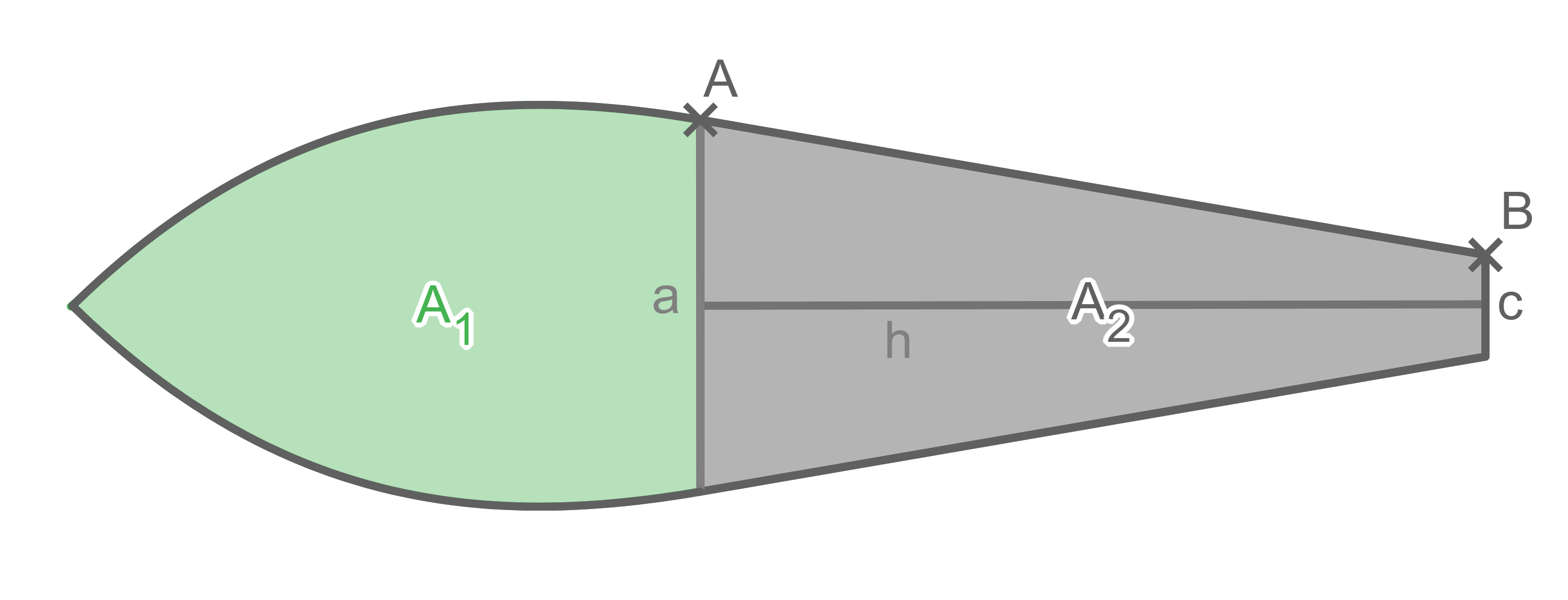
Hilfsskizze
1.4
Maximales Gewicht des Papiers berechnen
Der Gesamtflächeninhalt der Ballonhülle ergibt sich zu:

 Da
Da  des Gewichts für den Klebstoff benötigt werden, darf das Papier insgesamt höchstens
des Gewichts für den Klebstoff benötigt werden, darf das Papier insgesamt höchstens  wiegen.
wiegen.

 Das Papier darf maximal
Das Papier darf maximal  wiegen.
wiegen.
2.1
Der Graph von  verläuft für
verläuft für  oberhalb der
oberhalb der  -Achse. Somit ist
-Achse. Somit ist  für
für  streng monoton steigend. Anschließend verläuft der Graph von
streng monoton steigend. Anschließend verläuft der Graph von  für
für  unterhalb der
unterhalb der  -Achse. In diesem Bereich fällt der Graph von
-Achse. In diesem Bereich fällt der Graph von  also streng monoton.
An der Stelle
also streng monoton.
An der Stelle  besitzt
besitzt  eine Nullstelle mit Vorzeichenwechsel von positiv zu negativ, das heißt der Graph von
eine Nullstelle mit Vorzeichenwechsel von positiv zu negativ, das heißt der Graph von  hat dort einen Hochpunkt. Da der Graph von
hat dort einen Hochpunkt. Da der Graph von  in dem Intervall
in dem Intervall ![\([0;5,7]\)](https://mathjax.schullv.de/2bd5d420cda1705c73cf68a014f085f842bd8c785650031b2e9efc0d96c0e631?color=5a5a5a) mit den Koordinatenachsen eine Fläche von ungefähr
mit den Koordinatenachsen eine Fläche von ungefähr  einschließt, steigt der Graph von
einschließt, steigt der Graph von  bis zum Hochpunkt also um ca.
bis zum Hochpunkt also um ca.  Einheiten, das heißt der Ballon steigt um
Einheiten, das heißt der Ballon steigt um  Da der Ballon in einer Höhe von
Da der Ballon in einer Höhe von  startet, gilt
startet, gilt  und somit folgt
und somit folgt  als Extremwert.
als Extremwert.
2.2
Die Höhe, die der Ballon zum Zeitpunkt  hat, wird durch die Stammfunktion
hat, wird durch die Stammfunktion  von
von  beschrieben, für die
beschrieben, für die  gilt.
gilt.
Mit den Integrationsregeln folgt für eine Stammfunktion von


 Mit Hilfe der Anfangsbedingung von
Mit Hilfe der Anfangsbedingung von  folgt für
folgt für  Einsetzen von
Einsetzen von  liefert:
Zum Zeitpunkt
liefert:
Zum Zeitpunkt  befindet sich der Ballon ungefähr
befindet sich der Ballon ungefähr  über dem Boden.
über dem Boden.
Mit den Integrationsregeln folgt für eine Stammfunktion von
2.3
(1)
Die Funktion  beschreibt die Höhe des Ballons über dem Boden zum Zeitpunkt
beschreibt die Höhe des Ballons über dem Boden zum Zeitpunkt 
 bedeutet also, dass der Ballon zum Startzeitpunkt eine Höhe von
bedeutet also, dass der Ballon zum Startzeitpunkt eine Höhe von  besitzt.
besitzt.
(2)