A - Hilfsmittelfreier Teil

Analysis - Niveau 1

Gegeben ist die Funktion $f$ mit $f(x)= 2x^3-6x.$ Der Graph von $f$ ist in der folgenden Abbildung dargestellt.

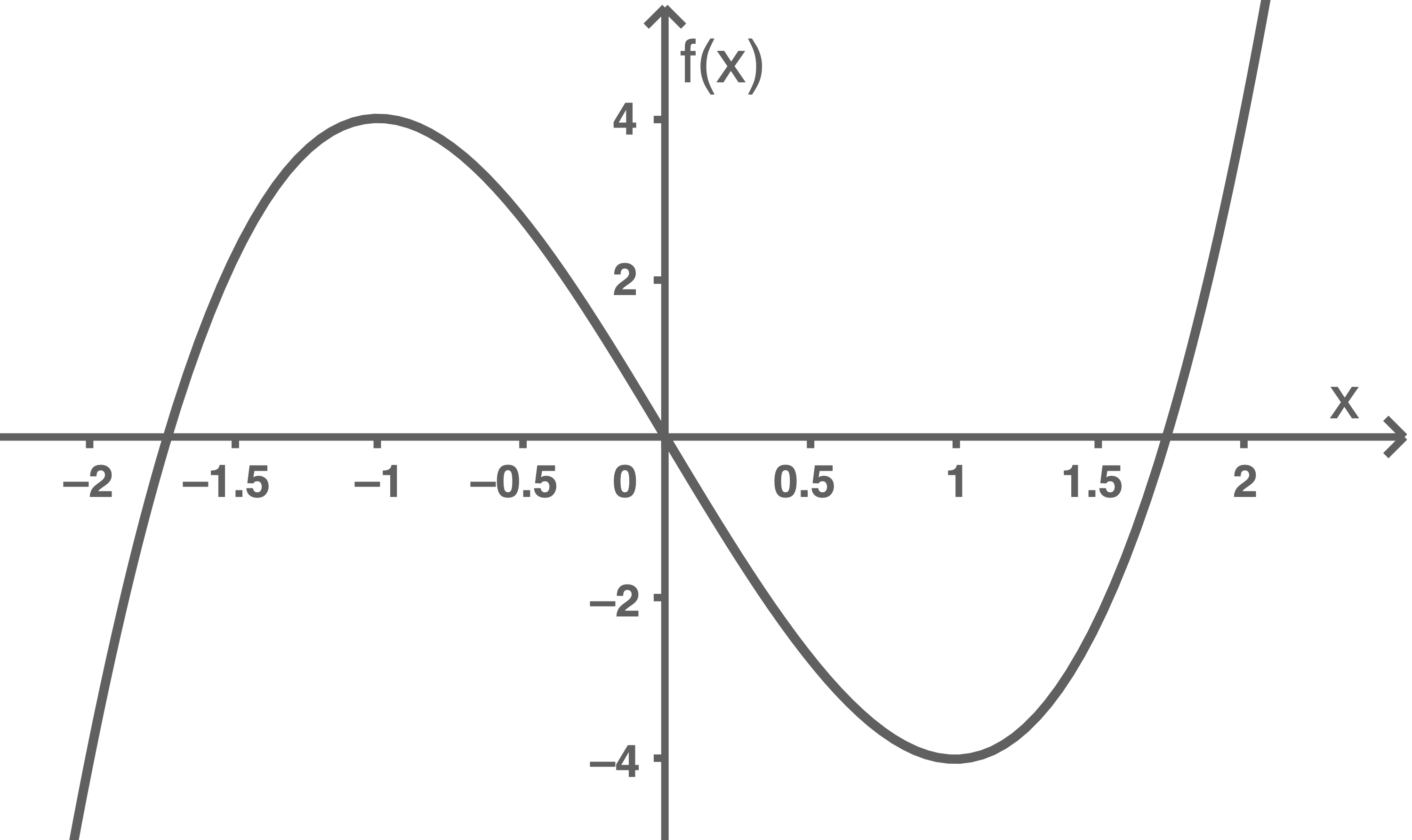
1.1

Berechne $\displaystyle\int_{0}^{2}f(x)\;\mathrm dx$ und begründe mit Hilfe des Materials, warum der Wert dieses Integrals negativ ist.

(4 BE)

1.2

Gib den Wert des Integrals $\displaystyle\int_{-a}^{a}f(x)\;\mathrm dx$ an.

(1 BE)

Lineare Algebra/Analytische Geometrie - Niveau 1

Gegeben ist das Dreieck $ABC$ mit den Punkten $A(2\mid 3\mid -4),$ $B(-1\mid1\mid 0)$ und $C(2\mid 1\mid -4).$

2.1

Zeige rechnerisch, dass das Dreieck im Punkt $C$ einen rechten Winkel hat.

(3 BE)

2.2

Berechne den Flächeninhalt der Dreiecksfläche.

(2 BE)

Stockastik - Niveau 1

Feline besitzt eine Kiste mit den sechs gleichartigen Kugeln 1 (weiß), 2 (schwarz), 3 (schwarz), 4 (weiß), 5 (schwarz), 6 (schwarz) und führt zwei verschiedene Experimente durch.

3.1

Sie zieht zweimal hintereinander zufällig eine Kugel und legt jede Kugel nach dem Zug wieder zurück in die Kiste.

Berechne die Wahrscheinlichkeit für das Ereignis
$A:$ Mindestens eine Kugel ist mit einer geraden Zahl beschriftet.

(2 BE)

3.2

Sie zieht dreimal hintereinander zufällig eine Kugel, ohne diese zurückzulegen.

Berechne die Wahrscheinlichkeit für das Ereignis
$B:$ Unter den gezogenen Kugeln ist genau eine weiße Kugel.

(3 BE)

Stochastik - Niveau 2

In einem Kindergarten mit 120 Kindern, darunter 68 Mädchen und 52 Jungen, befinden sich 14 Mädchen und 10 Jungen, die eine Brille tragen.

Eine Umfrage unter den Eltern aller Kinder ergibt, dass bei 30 Kindern beide Elternteile eine Brille tragen. Unter diesen 30 Kindern tragen 8 eine Brille.

4.1

Ermittle den Anteil der Kinder, die eine Brille tragen, unter allen Kindern dieses Kindergartens.

(2 BE)

4.2

Prüfe die beiden folgenden Ereignisse $A$ und $B$ auf stochastische Unabhängigkeit:

$A:$ Beide Elternteile tragen eine Brille.
$B:$ Kind trägt eine Brille.

Hinweis: Zwei Ereignisse $A$ und $B$ sind stochastisch unabhängig, falls gilt:
$P(B)=P_A(B)$ bzw. $P(A\cap B)= P(A)\cdot P(B)$

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$\displaystyle\int_{0}^{2}f(x)\;\mathrm dx=-4$

Rechenweg anzeigen

Der Wert des Integrals ist negativ, da im Intervall $[0;2]$ die Fläche zwischen der $x$ -Achse und der Funktion überwiegend unterhalb der $x$ -Achse liegt.

1.2

$\displaystyle\int_{-a}^{a}f(x)\;\mathrm dx=0S$

Rechnung anzeigen

Der Wert des Integrals $\displaystyle\int_{-a}^{a}f(x)\;\mathrm dx$ beträgt somit Null.

Dies kann auch direkt an der Punktsymmetrie der Funktion um den Ursprung erkannt werden.

2.1

Es gilt:

$\overrightarrow{AC} \circ \overrightarrow{BC}=0$

Rechenweg anzeigen

Da das Skalarprodukt Null ergibt, hat das Dreieck im Punkt $C$ einen rechten Winkel.

2.2

$\begin{array}[t]{rll} A&=&\dfrac{1}{2} \cdot \mid\overrightarrow{AC}\mid \cdot \mid \overrightarrow{BC} \mid & \\[5pt] &=& \dfrac{1}{2} \cdot \sqrt{(-2)^2 } \cdot \sqrt{3^2 + (-4)^2}& \\[5pt] &=& \dfrac{1}{2} \cdot 2 \cdot 5 & \\[5pt] &=& 5 \end{array}$

Der Flächeninhalt $A$ der Dreiecksfläche beträgt folglich $5\,\text{FE}.$

3.1

Die Wahrscheinlichkeit, eine Kugel mit einer geraden Zahl zu ziehen, beträgt $p=\dfrac{1}{2}.$

$G \mathrel{\widehat{=}}\text{Kugel mit gerader Zahl}$

Es folgt also:

$P(A)= \dfrac{3}{4}$

Rechenweg anzeigen

Die Wahrscheinlichkeit für das Ereignis $A$ beträgt somit $75\,\%.$

3.2

Die Wahrscheinlichkeit, eine weiße Kugel zu ziehen, beträgt $\dfrac{2}{6}.$

$W \mathrel{\widehat{=}}\text{weiße Kugel}$

$P(B)=\dfrac{3}{5}$

Rechenweg anzeigen

Die Wahrscheinlichkeit für das Ereignis $B$ beträgt $60\,\%.$

4.1

$B \mathrel{\widehat{=}}\text{Kinder, die eine Brille tragen}$

$P(B) = \dfrac{14+10}{120} = \dfrac{24}{120} = \dfrac{1}{5}$

4.2

$A$ und $B$ sind genau dann stochastisch unabhängig, wenn der Anteil an Kindern mit Brille von Eltern mit Brille gleich dem Anteil aller Kinder mit Brille an allen Kindern ist.

Die Anzahl der Kinder mit Brille, deren beide Eltern eine Brille tragen, ist in der Aufgabenstellung gegeben durch $P_{A}(B)=\dfrac{8}{30}.$

Es ergibt sich zudem, dass unter den 120 Kindern im Kindergarten insgesamt 24 Kinder eine Brille tragen.

Somit folgt:

$P_{A}(B) = \dfrac{8}{30} \neq \dfrac{1}{5} = P(B)$

$A$ und $B$ sind somit nicht stochastisch unabhängig.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?