B1 - Analysis

An einem geradlinig verlaufenden Fluss steht ein Deich älteren Baujahres, der erhöht werden soll, um den Hochwasserschutz zu verbessern. Das horizontale ebene Gelände links und rechts des Deichs liegt bei der folgenden Modellierung auf der Höhe der $x$ -Achse.

Die Funktionswerte der folgenden Funktionen geben die Höhen des Deichs in Bezug auf dieses ebene Gelände an. Eine Einheit im Koordinatensystem entspricht einem Meter.

Die obere Profillinie des alten Deichs wird für $0\leq x \leq 20$ durch den Graphen der Funktion $f$ mit $f(x)= \dfrac {3}{4}\cdot x \cdot \mathrm{e}^{1- \frac{1}{4}x}$ beschrieben.

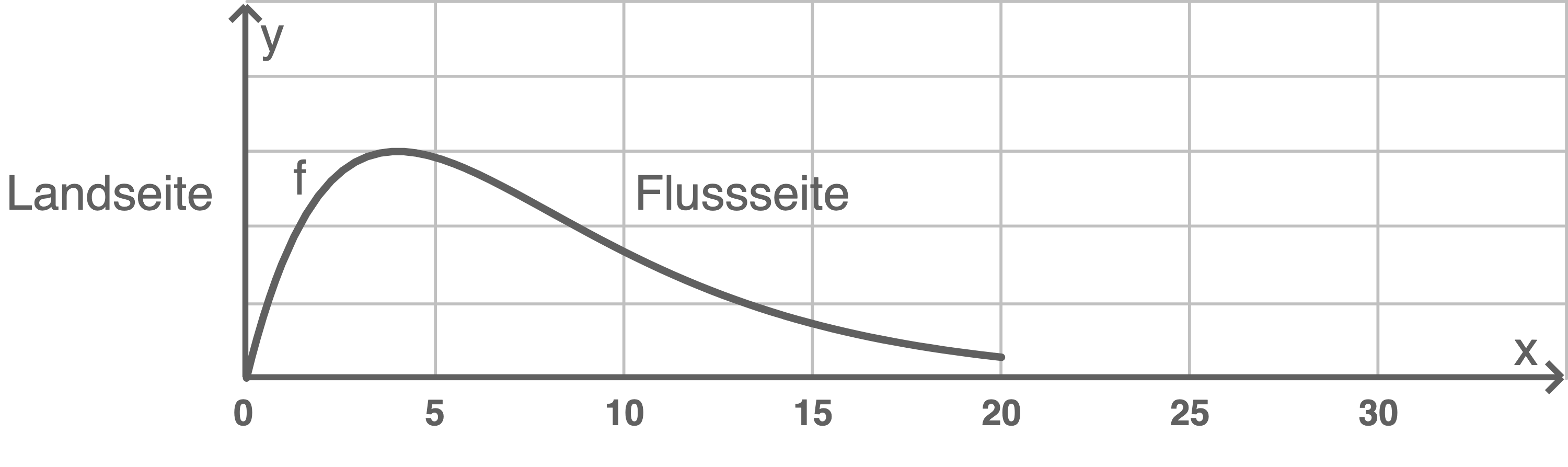Für $20\leq x \leq x_N$ wird die obere Profillinie des Deichs durch die Tangente $t$ an den Graphen von $f$ im Punkt $P(20\mid f(20))$ beschrieben, wobei $x_N$ die Nullstelle der Tangente $t$ bezeichnet.

1.1

Berechne die Funktionsgleichung der Tangente $t.$

Zeige, dass der Deich eine Breite von $25\,\text{m}$ besitzt.

Zeichne die Tangente im Bereich $20\leq x\leq x_N$ in das Koordinatensystem aus der Aufgabenstellung ein.

$\bigg[$ zur Kontrolle: $t(x)=-\dfrac{3}{\mathrm{e}^4}\cdot x+\dfrac{75}{\mathrm{e}^4} \bigg]$

(9 BE)

1.2

Bestimme den höchsten Punkt der Profillinie des Deichs. Die Untersuchungen der notwendigen Bedingungen ist hierbei ausreichend.

Beschrifte die $y$ -Achse im Koordinatensystem aus der Aufgabenstellung mit einer geeigneten Skalierung.

(4 BE)

1.3

Berechne mithilfe des Formansatzes $F(x)= (a \cdot x + b ) \cdot \mathrm e ^{1- \frac{1}{4}x}$ eine Stammfunktion der Funktion $f.$

$\bigg[$ zur Kontrolle: $F(x)=(-3\cdot x-12)\cdot \mathrm e^{1-\frac{1}{4} x}\bigg]$

(5 BE)

1.4

Berechne das Volumen des gesamten Erdreichs, das zum Bau des $1\,\text{km}$ langen alten Deichs aufgeschüttet wurde.

(5 BE)

Der alte Deich soll nun durch einen neuen, gleich langen aber höheren Deich ersetzt werden, dessen obere Profillinie für $0\leq x\leq 25$ durch den Graphen einer Funktion $g$ beschrieben wird, wobei $g$ eine Funktion der Funktionenschar $g_k$ mit $g_k(x)=\dfrac{k}{1000}\cdot x\cdot (x-25)^2$ für $k\gt 0$ ist.

Die Hochpunkte der Graphen der Funktionenschar $g_k$ liegen in Abhängigkeit vom Parameter $k$ bei $H\bigg(\dfrac{25}{3}\,\bigg \vert \,\dfrac{125}{54}k\bigg).$

2.1

Gib an, welchen Einfluss der Parameter $k$ auf die Höhe und auf die Breite des neuen Deichs besitzt. Berücksichtige dabei auch die Lage der Nullstellen.

Berechne, wie der Parameter $k$ gewählt werden muss, damit der neue Deich höher als $3\,\text{m}$ ist.

(3 BE)

2.2

Zeige, dass die Graphen der Funktionsschar $g_k$ unabhängig vom Parameter $k$ einen Wendepunkt an der Stelle $x_w=\dfrac{50}{3}$ besitzen.
$\bigg[$ zur Kontrolle: $\(g_k$

(6 BE)

2.3

Moderne Deiche werden mit einem möglichst flachen Gefälle auf der Flussseite konstruiert.

Für den Steigungswinkel $\alpha$ des (flussseitigen) Deichprofils gegenüber der Horizontalen soll $\mid\alpha\mid\leq 30^{\circ}$ gelten.

Berechne, für welchen Wert des Parameters $k$ der Graph der Funktionenschar $g_k$ die Bedingung $\mid \alpha\mid=30^{\circ}$ an der steilsten Stelle des (flussseitigen) Deichprofils erfüllt.

(4 BE)

2.4

Für die Profillinie des neuen Deichs wird die Funktion $g$ mit $g(x)=g_2(x)$ gewählt und die Rechnung im unten stehenden Kasten durchgeführt.

Erläutere mit Hilfe der folgenden Abbildung die Rechenschritte und deute das Ergebnis in Zeile (2) im Sachzusammenhang.

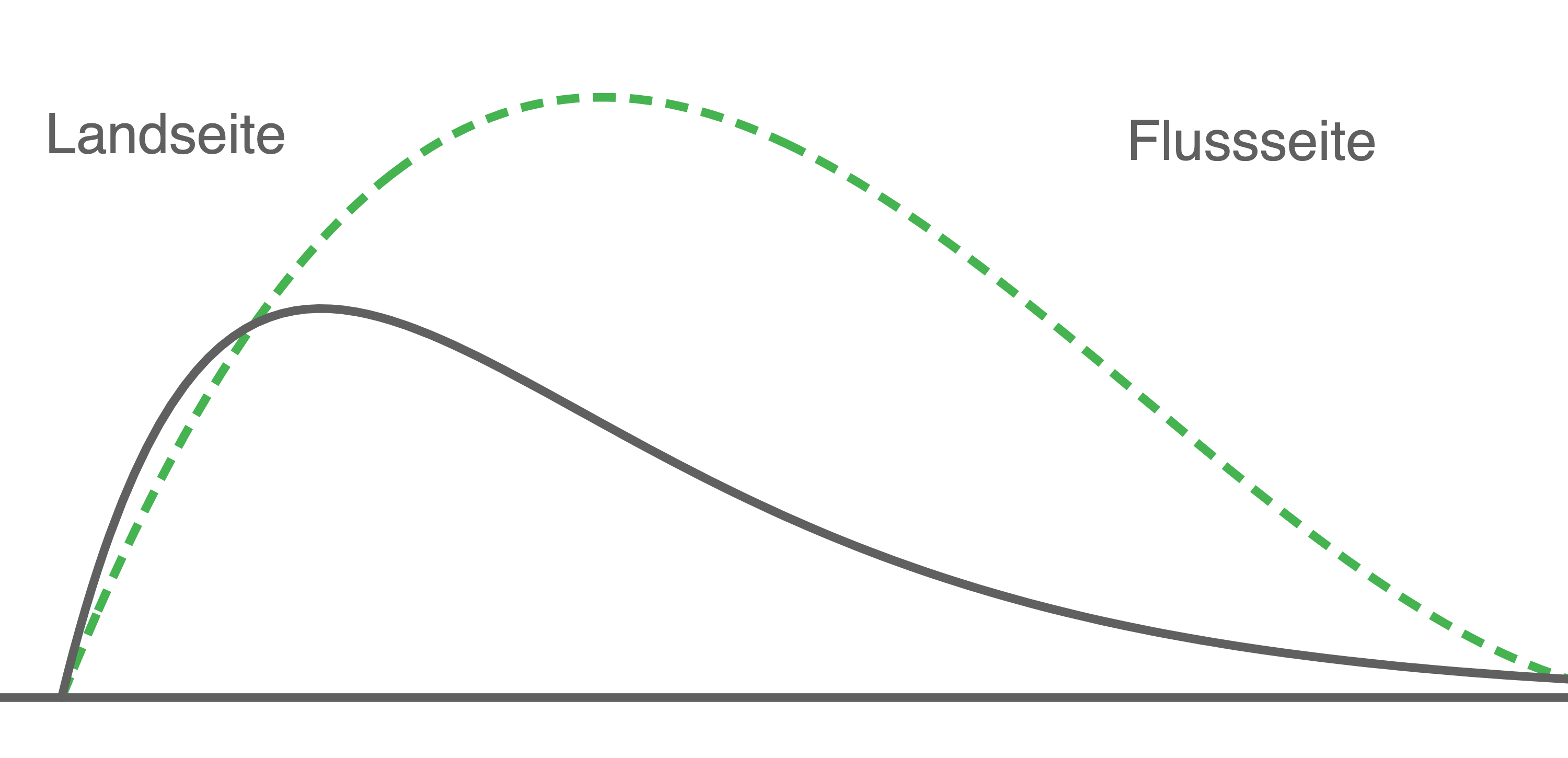
(4 BE)

Rechenschritte anzeigen

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Tangentengleichung berechnen

Mit der Produkt- und Kettenregel ergibt sich die Ableitung $\(f$ mit:

Vollständigen Rechenweg anzeigen

Die allgemeine Tangentengleichung lautet $t(x) = m \cdot x + c$ .

Somit gilt:

$\begin{array}[t]{rll} f(20) &=& \dfrac{3}{4} \cdot 20 \cdot \mathrm{e}^{1-\frac{1}{4} \cdot 20}& \\[5pt] &=& 15 \cdot \mathrm{e}^{-4}& \\[5pt] &=& \dfrac{15}{\mathrm{e}^4} & \\[5pt] \end{array}$

$\(\begin{array}[t]{rll} f$

Einsetzen der Werte in die allgemeine Tangentengleichung ergibt:

$\(\begin{array}[t]{rll} f$

Somit ergibt sich folgende Tangentengleichung:

$t(x) = -\dfrac{3}{\mathrm{e}^4} x + \dfrac{75}{\mathrm{e}^4}$

Breite des Deichs nachweisen

Die Breite des Deichs entspricht der Nullstelle der Tangente.

Nullstelle berechnen:

$\begin{array}[t]{rll} t(x)&=& 0 & \\[5pt] -\dfrac{3}{\mathrm{e}^4} x + \dfrac{75}{\mathrm{e}^4}&=& 0&\quad \scriptsize \mid\; +\dfrac{3}{\mathrm{e}^4} x \\[5pt] \dfrac{75}{\mathrm{e}^4}&=& \dfrac{3}{\mathrm{e}^4}x&\quad \scriptsize \mid\;\cdot \dfrac{\mathrm{e}^4}{3} \\[5pt] 25&=& x \end{array}$

Der Deich besitzt folglich eine Breite von $25\,\text{m}.$

Tangente einzeichnen

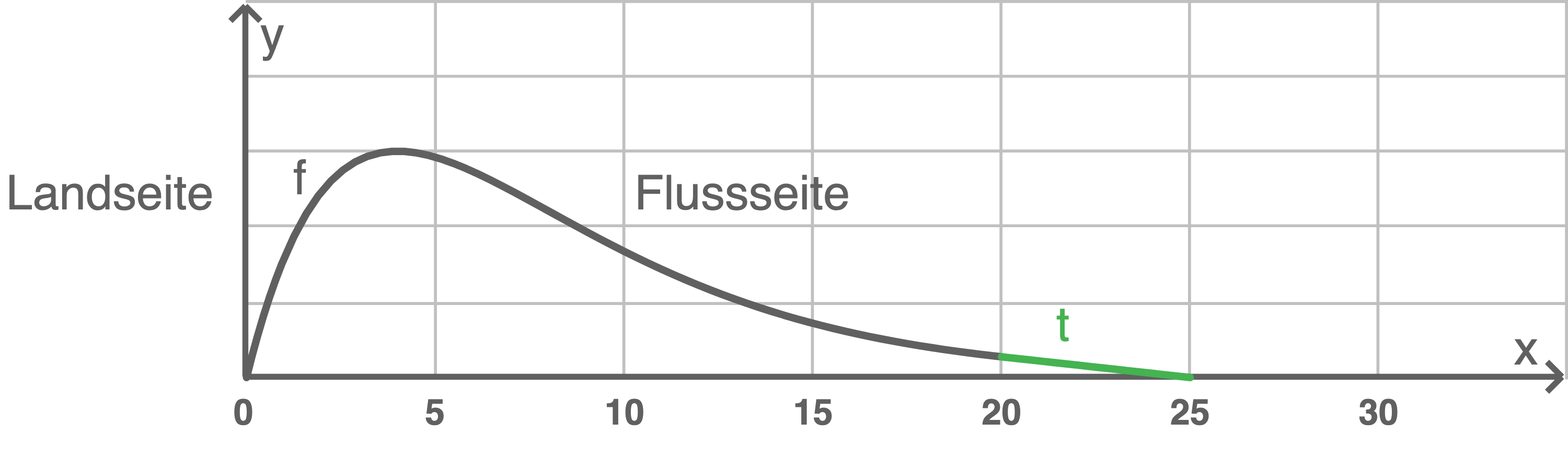
1.2

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

Da $\dfrac{3}{4} \cdot \mathrm{e}^{1- \frac{1}{4}\cdot x} \gt 0$ gilt, folgt:

$\begin{array}[t]{rll} 1-\dfrac{1}{4}x&=& 0& \quad \scriptsize \mid +\dfrac{1}{4}x \quad \scriptsize \mid \cdot 4 \\[5pt] 1&=& \dfrac{1}{4}x& \quad \scriptsize \mid \cdot 4 \\[5pt] 4&=& x \end{array}$

Laut Aufgabenstellung genügt die Untersuchung der notwendigen Bedingung. Die hinreichende Bedingung muss folglich nicht mehr geprüft werden.

2. Schritt: $y$ -Koordinate berechnen

$\begin{array}[t]{rll} f(4)&=& \dfrac{3}{4} \cdot 4 \cdot \mathrm{e}^{1-\frac{1}{4} \cdot 4}&\\[5pt] &=& 3 \cdot \mathrm{e}^{0} &\\[5pt] &=& 3&\\[5pt] \end{array}$

Der höchste Punkt des Deichs hat somit die Koordinaten $P(4\mid3).$

Koordinatensystem beschriften

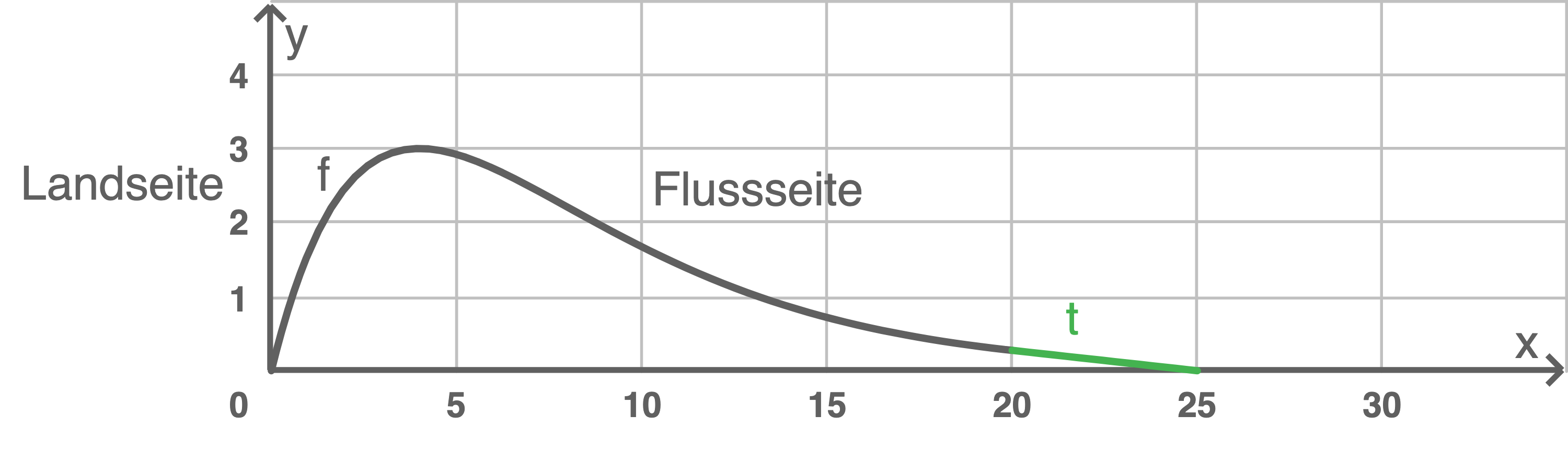
Skalierung Koordinatensystem Hessen Abi 2021

1.3

Für die Stammfunktion $F(x)$ muss gelten:

$\( F$

Rechnung anzeigen

Damit Gleichheit gilt, müssen die Terme, die $x$ enthalten, auf beiden Seiten gleich sein. Es soll also gelten:

$\begin{array}[t]{rll} - \dfrac{a}{4}x&= \dfrac{3}{4}x& \quad \scriptsize \mid \cdot (-4) \quad \scriptsize \mid :x \\[5pt] a&= -3& \end{array}$

Einsetzen in die obere Gleichung ergibt:

$b=-12$

Rechenweg anzeigen

Einsetzen der Werte von $a$ und $b$ in den Formansatz liefert nun eine Stammfunktion von $f:$

$F(x) = (-3x -12) \cdot \mathrm{e}^{1- \frac{1}{4}x}$

1.4

Der Flächeninhalt der Querschnittsfläche $A$ des Deichs setzt sich wie folgt zusammen:

$A=\displaystyle\int_{0}^{20}f(x)\;\mathrm dx + \displaystyle\int_{20}^{25}t(x)\;\mathrm dx$

$\displaystyle\int_{0}^{20}f(x)\;\mathrm dx= -\dfrac{72}{\mathrm{e}^4} +12\mathrm{e}$

Rechenweg anzeigen

$\displaystyle\int_{20}^{25}t(x)\;\mathrm dx= \dfrac{75}{2\mathrm{e}^4}$

Rechenweg anzeigen

Es folgt also:

$\begin{array}[t]{rll} A&=& -\dfrac{72}{\mathrm{e}^4} +12\mathrm{e} + \dfrac{75}{2\mathrm{e}^4}& \\[5pt] &\approx & 31,99 \; [\,\text{m}^2] \end{array}$

Da der Deich $1\,\text{km}$ lang ist, folgt das Volumen mit:

$V = 1000 \,\text{m} \cdot 31,99\,\text{m}^2 = 31990 \; \text{m}^3$

2.1

Einfluss angeben

Umformen von $g_{k}$ ergibt:

$\begin{array}[t]{rll} g_{k}(x)&=& \dfrac{k}{1000} \cdot x \cdot (x-25)^2& \\[5pt] &=& k \cdot \dfrac{x}{1000} \cdot (x^2 - 50x +625)& \\[5pt] &=& k \cdot \left(\dfrac{x^3 - 50x^2 + 625x}{1000}\right)& \\[5pt] \end{array}$

Aus dem Funktionsterm geht nun hervor, dass der Parameter $k$ den Graphen der Funktion entlang der $y$ -Achse streckt beziehungsweise staucht.

Da $k \gt 0$ gilt, hat $k$ also keinen Einfluss auf die Nullstellen und somit auch nicht auf die Streckung beziehungsweise Stauchung des Graphen entlang der $x$ -Achse.

Der Parameter $k$ hat folglich Einfluss auf die Höhe des Deichs, jedoch nicht auf die Breite.

Parameter bestimmen

Damit der neue Deich höher als $3\,\text{m}$ ist, muss die $y$ -Koordinate des Hochpunkts von $H$ größer als $3$ sein:

$\begin{array}[t]{rll} \dfrac{125}{54} \cdot k& \gt 3& \quad \scriptsize \,\big \vert \, \cdot \dfrac{54}{125} \\[5pt] k& \gt \dfrac{162}{125}& \\[5pt] k& \gt 1,296& \\[5pt] \end{array}$

Somit muss $k \gt 1,296$ gewählt werden, sodass der Deich höher als $3\,\text{m}$ ist.

2.2

1. Schritt: Ableitungen bestimmen

$g_{k}(x)=\dfrac{k}{1000} \cdot x \cdot (x-25)^2$

Umformungen anzeigen

$\(\begin{array}[t]{rll} g_{k}$

2. Schritt: Notwendige Bedingung für Wendestellen anwenden

$\(\begin{array}[t]{rll} g_{k}$

3. Schritt: Hinreichende Bedingung für Wendestellen anwenden

$\(g_{k}$

Wegen $k\gt 0$ liegt somit unabhängig von $k$ an der Stelle $x_w=\dfrac{50}{3}$ eine Wendestelle vor.

2.3

Die steilste Stelle eines Funktionsgraphens entspricht seiner Wendestelle. Da sich die Wendestelle $x_{w}$ aus Aufgabenteil 2.2 auf der Flussseite befindet und es keinen weiteren flussseitigen Wendepunkt gibt, befindet sich die steilste flussseitige Stelle bei $x_{w}$ .

Steigung an der Wendestelle berechnen:

$\( g_{k}$

Rechenweg anzeigen

Für den Steigungswinkel $\mid\alpha\mid =30^{\circ}$ gilt:

$\(\begin{array}[t]{rll} m &=& \tan(\alpha)& \\[5pt] \mid g$

Für $k\approx 2,77$ erfüllt der Graph der Funktionenschar $g_k$ somit die Bedingung $\mid\alpha\mid =30^{\circ}$ an der steilsten Stelle des flusseitigen Deichprofils.

2.4

$(1)$ Im ersten Rechenschritt werden die Schnittstellen von $f(x)$ und $g_{2}(x)$ berechnet. Dabei liegt der Fokus auf den landseitigen Schnittstellen.

$(2)$ Im zweiten Rechenschritt wird die Fläche berechnet, die $f(x)$ und $g_{2}(x)$ zwischen ihren Schnittpunkten $x_{1} = 0$ und $x_{2}=3$ einschließen. Im Sachzusammenhang ist das genau die Fläche, die landseitig vom alten Deich abgetragen werden muss, um das Profil des neuen Deichs zu kreieren.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?