C1 - Lineare Algebra, Analytische Geometrie
1
Der „PeaQ-Tanztempel" in Mainz-Hechtsheim ist eine Lokalität, die man für Veranstaltungen mieten kann. Das zweite Bild zeigt einen Planungsentwurf für ein ähnliches Gebäude, das aus einer quadratischen Pyramide mit einer Grundseite der Länge  und einem parallel zur
und einem parallel zur  -Achse ausgerichteten Vorbau mit rechteckiger Grundfläche und symmetrischem Dach besteht. Der Ursprung des Koordinatensystems liegt in der Mitte der Grundfläche der Pyramide. Es sind der Punkt
-Achse ausgerichteten Vorbau mit rechteckiger Grundfläche und symmetrischem Dach besteht. Der Ursprung des Koordinatensystems liegt in der Mitte der Grundfläche der Pyramide. Es sind der Punkt  der Grundfläche und die Spitze
der Grundfläche und die Spitze  der Pyramide gegeben.
der Pyramide gegeben.
Alle Einheiten sind in Meter angegeben.

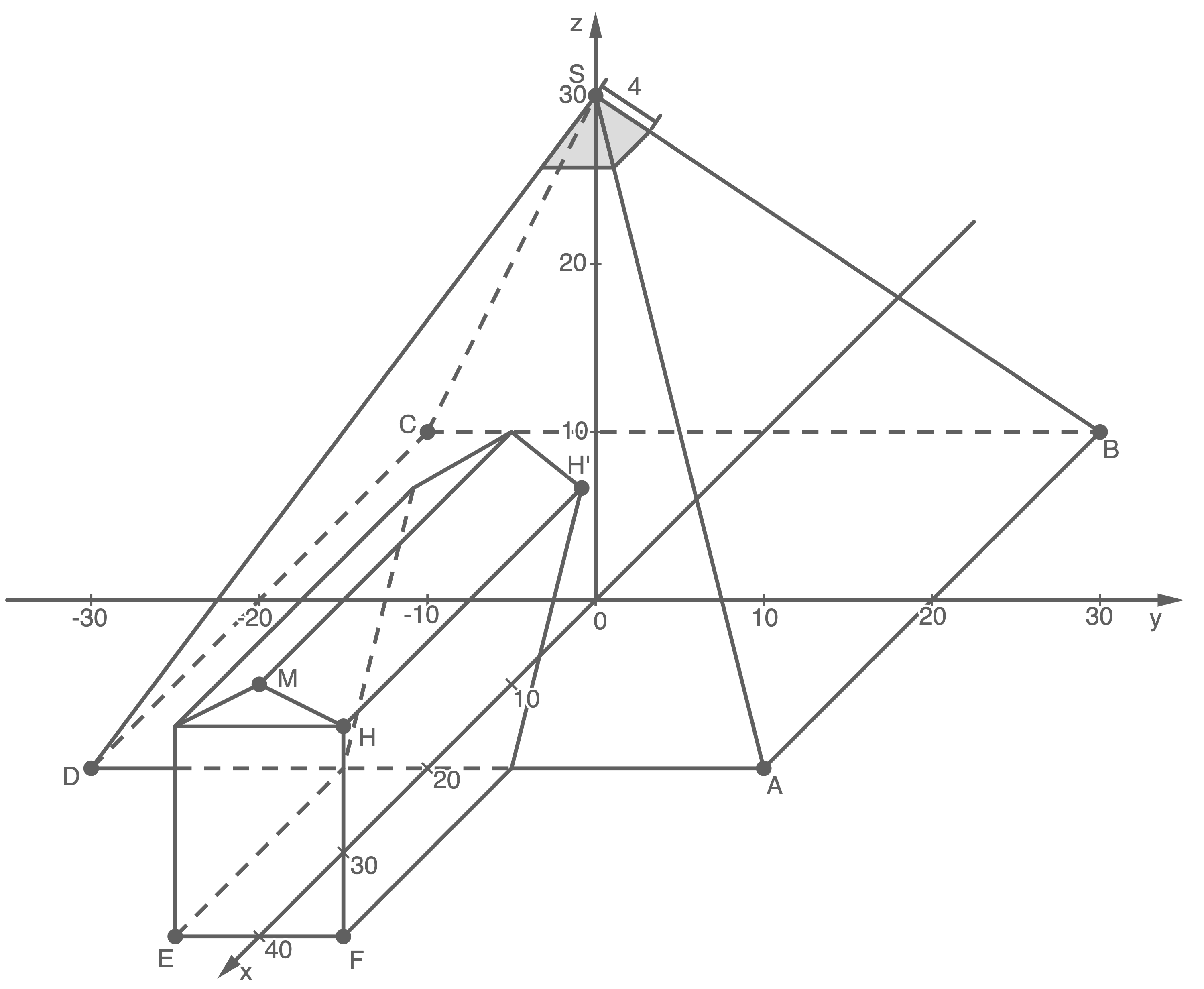
Alle Einheiten sind in Meter angegeben.

Der „PeaQ-Tanztempel“ in Mainz-Hechtsheim.

Planungsentwurf
1.1
Gib die Koordinaten der Punkte  und
und  an.
an.
(2 BE)
1.2
Berechne das Volumen der Pyramide.
(2 BE)
1.3
Entlang der vier Seitenkanten der Pyramide werden Lichterketten angebracht. Berechne die Gesamtlänge der Lichterketten.
(3 BE)
1.4
Berechne den Winkel an der Spitze eines Seitendreiecks der Pyramide.
[zur Kontrolle:  ]
]
(3 BE)
1.5
Die Spitze der Pyramide ist mit Metall verkleidet. Die Seitenkanten dieser ebenfalls quadratischen Pyramide sind  lang (siehe Planungsentwurf). Berechne die Größe der Fläche, die mit Metall verkleidet ist.
lang (siehe Planungsentwurf). Berechne die Größe der Fläche, die mit Metall verkleidet ist.
(4 BE)
1.6
Die Seitenfläche der Pyramide mit den Eckpunkten  und
und  liegt in der Ebene
liegt in der Ebene  .
.
Gib eine Parameterform der Ebene an und bestimme eine zugehörige Koordinatengleichung.
[zur Kontrolle: Eine mögliche Koordinatengleichung lautet
an und bestimme eine zugehörige Koordinatengleichung.
[zur Kontrolle: Eine mögliche Koordinatengleichung lautet  .]
.]
Gib eine Parameterform der Ebene
(6 BE)
2
Im Folgenden wird das Dach des Vorbaus betrachtet. Von der Vorderseite dieses Daches sind die Punkte  und
und  gegeben.
gegeben.
2.1
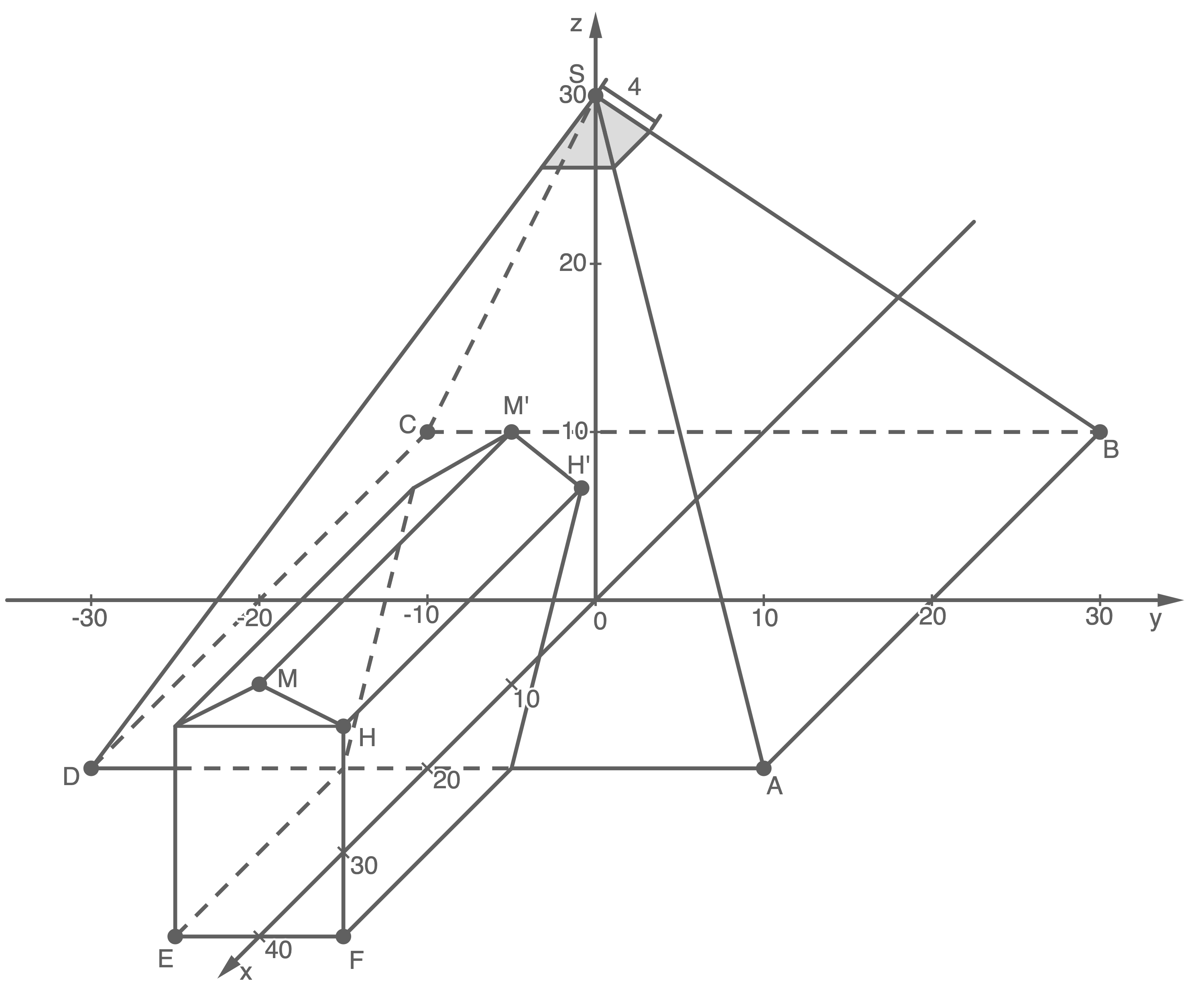
Zeige, dass der Punkt  auf der Ebene
auf der Ebene  liegt, und begründe ohne weitere Rechnung, dass es sich bei dem Punkt
liegt, und begründe ohne weitere Rechnung, dass es sich bei dem Punkt  um denjenigen Punkt handeln muss, in dem der (durch den Punkt
um denjenigen Punkt handeln muss, in dem der (durch den Punkt  verlaufende) Dachfirst des Vorbaus auf die Pyramide trifft. Beschrifte den Punkt
verlaufende) Dachfirst des Vorbaus auf die Pyramide trifft. Beschrifte den Punkt  im Planungsentwurf.
im Planungsentwurf.
(4 BE)
2.2
Berechne die Koordinaten des Punktes  , bei dem die Dachkante des Vorbaus, die durch den Punkt
, bei dem die Dachkante des Vorbaus, die durch den Punkt  verläuft, auf die Pyramide trifft.
[zur Kontrolle:
verläuft, auf die Pyramide trifft.
[zur Kontrolle:  ]
]
(4 BE)
2.3
Untersuche, um welche Art von Viereck es sich bei der Dachfläche  handelt, und bestimme den Flächeninhalt der Dachfläche
handelt, und bestimme den Flächeninhalt der Dachfläche 

 .
.
(6 BE)
3
Ein Besucher nähert sich dem Pyramideneingang entlang der  -Achse aus positiver Richtung. Die Augenhöhe des Besuchers ist
-Achse aus positiver Richtung. Die Augenhöhe des Besuchers ist  über dem Boden. Erläutere die Rechnung in den Zeilen (1) bis (3) im untenstehenden Kasten und erkläre die Bedeutung des Punktes
über dem Boden. Erläutere die Rechnung in den Zeilen (1) bis (3) im untenstehenden Kasten und erkläre die Bedeutung des Punktes  aus Zeile (4) im Sachzusammenhang.
aus Zeile (4) im Sachzusammenhang.
 ,
, 

 ,
, 




Bildnachweise [nach oben]
(1)
(2)
(3)
(4)
(6 BE)
© - https://www.pyramidemainz.de/die-pyramide
1.1
1.2
Das Volumen kann mit der Volumenformel für Pyramiden berechnet werden. Aus den Koordinaten für die Spitze folgt, dass die Pyramide  m hoch ist.
m hoch ist.

![\(V= \dfrac {1}{3} \cdot 40^2 \cdot 30 = 16000 \text{[m}^3\text{]}\)](https://mathjax.schullv.de/e4aa60679a733ad63d54ff0bcf4503b1a153fc767d33cbe619732640837d5c1c?color=5a5a5a)
1.3
Die Pyramide hat 4 Seitenkanten der gleichen Länge.




![\(\approx 164,92\text{[m]}\)](https://mathjax.schullv.de/b132c6a203493aeec2fc6c1a1b4fbe8ae94e7b8c62f49419332d6c0b6f9216e3?color=5a5a5a) Die Lichterkette muss ca.
Die Lichterkette muss ca.  lang sein.
lang sein.
1.4
Ein Seitendreieck besteht z.B. aus den Punkten  ,
,  und
und  . Es folgt:
. Es folgt:
![\(\begin{array}[t]{rll}
\cos(\alpha)&=& \dfrac{\left| \overrightarrow{ SD} \circ \overrightarrow{ SA}\right|}{\,\bigg \vert \, \overrightarrow{ SD}\,\bigg \vert \, \cdot \,\bigg \vert \, \overrightarrow{ SA}\,\bigg \vert \,} \\[5pt]
&=& \dfrac {\left | \pmatrix{20\\-20\\-30}\circ \pmatrix{20\\20\\-30} \right|}{\left | \pmatrix{20\\-20\\-30}\right| \cdot \left | \pmatrix{20\\20\\-30} \right|} \\[5pt]
&=& \dfrac{900}{1700} \\[5pt]
&=& \dfrac {9}{17}
\end{array}\)](https://mathjax.schullv.de/6e911b22a2f6d4431eb5348ac9ae2d6217c63aefe7db2713477289280da3dd73?color=5a5a5a) Es folgt:
Es folgt:

1.5
Da der Flächeninhalt der Seitenfläche der Metallpyramide aus vier gleichen Dreiecken besteht, kann dieser mithilfe der Gleichung  berechnet werden. Hierbei ist
berechnet werden. Hierbei ist  die Grundkante der jeweiligen Dreiecke und
die Grundkante der jeweiligen Dreiecke und  die Höhe dieser.
Es gilt:
die Höhe dieser.
Es gilt:



![\(\approx 3,88 [\text{m}]\)](https://mathjax.schullv.de/ef12067491eb274ca10a6f815df2c74a770047822679e359663fcf5d55f769d2?color=5a5a5a)



![\(\approx 3,5 [\text{m}]\)](https://mathjax.schullv.de/69f0aa2c174c5e75f9b1980cea7cc59786b99517af03649fe190f5097e8a50be?color=5a5a5a) Für den Flächeninhalt der Seitenfläche folgt:
Für den Flächeninhalt der Seitenfläche folgt:



![\(\approx 27,16 \; [\text{m}^2]\)](https://mathjax.schullv.de/9d8b422ea1c1a00c657072f3ee0a07d5c2cb9e9ebb027456406f0a0f7c5b45c3?color=5a5a5a)
1.6
2.1
Punktprobe: Einsetzen von  in die Ebene
in die Ebene 
![\(\begin{array}[t]{rll}
3\cdot 10+2\cdot 15&=& 60 \\[5pt]
60&=&60
\end{array}\)](https://mathjax.schullv.de/c261c34d1f9606e8b298b42a3477b0a367abfd2177fb218aed6785caf2537f4e?color=5a5a5a) Hieraus folgt
Hieraus folgt  .
Die Punkte
.
Die Punkte  und
und  stimmen in den
stimmen in den  - und
- und  - Koordinaten überein. Daher liegen sie auf einer Geraden, die parallel zur
- Koordinaten überein. Daher liegen sie auf einer Geraden, die parallel zur  -Achse verläuft. Deshalb ist der Punkt
-Achse verläuft. Deshalb ist der Punkt  der Punkt, auf dem der Vorbau auf die Pyramide trifft.
der Punkt, auf dem der Vorbau auf die Pyramide trifft.

2.2
Die Dachkante verläuft parallel zur  -Achse und somit entlang des Richtungsvektors
-Achse und somit entlang des Richtungsvektors  durch den Punkt
durch den Punkt  Eine Geradengleichung der Dachkante ergibt sich also zu:
Eine Geradengleichung der Dachkante ergibt sich also zu:
![\(\begin{array}[t]{rlll}
h:\overrightarrow{x}&=& \pmatrix{40\\5\\12,5} +r \cdot \pmatrix{1\\0\\0}&\mid\; \\[5pt]
&=& \pmatrix{40+r\\5\\12,5}
\end{array}\)](https://mathjax.schullv.de/aa38680966222bd931264c5c456969c5842a2552caf3d467a39c719bd02a27ff?color=5a5a5a) Einsetzen des allgemeinen Geradenpunkts in
Einsetzen des allgemeinen Geradenpunkts in  liefert:
liefert:
![\(\begin{array}[t]{rlll}
3\cdot (40+r) + 2\cdot 12,5&=& 60 &\mid\; \\[5pt]
120+3r + 25&=& 60 &\mid\; -60 \\[5pt]
85-3r &=& 0 &\mid\; -3r \\[5pt]
85 &=& -3r &\mid\; :(-3) \\[5pt]
-\frac{85}{3}&=& r
\end{array}\)](https://mathjax.schullv.de/4badbf1e36be56a368f762f904b5947bfac5a9e0e87bae1021f3ef5109c10e05?color=5a5a5a) Durch Einsetzen von
Durch Einsetzen von  in
in  folgt:
folgt:
![\(\begin{array}[t]{rlll}
h: \overrightarrow{x}&=& \pmatrix{40\\5\\12,5} - \frac{85}{3} \cdot \pmatrix{1\\0\\0}& \\[5pt]
&=&\pmatrix{\frac{35}{3} \\5\\ \frac{25}{2}}
\end{array}\)](https://mathjax.schullv.de/5ba65981a8a0a6333920a5e2473b7b880bafa773244aa21359b8e934caed2d89?color=5a5a5a) Die Koordinaten des Punktes
Die Koordinaten des Punktes  sind somit gegeben durch
sind somit gegeben durch 
2.3
Die Kanten  und
und  verlaufen parallel zueinander und parallel zur x-Achse.
verlaufen parallel zueinander und parallel zur x-Achse.
 und
und 
Die geometrische Form des Vierecks ist ein Trapez, da .
Da
.
Da  und
und  die gleiche
die gleiche  -Koordinate haben, gilt für die Höhe des Trapez:
-Koordinate haben, gilt für die Höhe des Trapez:
![\(\left| \overline{MH}\right | = \left| \pmatrix{0\\5\\-2,5}\right|
=\sqrt{31,25} \approx 5,59 \; [\text{m}]\)](https://mathjax.schullv.de/3eeacbc8736cf420d2833ea4c73e2483152d084c3ae64c8c8c0b05a583936974?color=5a5a5a) Mit der Formel für den Flächeninhalt eines Trapezes folgt:
Mit der Formel für den Flächeninhalt eines Trapezes folgt:
![\(\begin{array}[t]{rlll}
A&=& \dfrac{1}{2} \cdot \left(\left| \overline{MM](https://mathjax.schullv.de/d5116331e5d97cb8b7e1b71b830948500927048c71ccea71a870fbe207c70c1b?color=5a5a5a)
Die geometrische Form des Vierecks ist ein Trapez, da
3.1
In (1) wird durch die Punkte  und
und  eine Gleichung
eine Gleichung  angegeben.
In Zeile (2) wird mit der
angegeben.
In Zeile (2) wird mit der  -Koordinate, die den Wert
-Koordinate, die den Wert  hat, der Wert des Geradenparameters berechnet.
Der Geradenparameter wird in Zeile (3) eingesetzt in die Gerade, wodurch sich der Punkt ergibt, der als
hat, der Wert des Geradenparameters berechnet.
Der Geradenparameter wird in Zeile (3) eingesetzt in die Gerade, wodurch sich der Punkt ergibt, der als  -Koordinate den Wert
-Koordinate den Wert  hat.
Der Punkt
hat.
Der Punkt  aus Zeile (4) ist die Standposition eines Besuchers auf dem Boden, wenn er sich der Pyramide nähert und die Spitze
aus Zeile (4) ist die Standposition eines Besuchers auf dem Boden, wenn er sich der Pyramide nähert und die Spitze  nicht mehr sehen kann, da diese durch den Vorbau verdeckt wird.
nicht mehr sehen kann, da diese durch den Vorbau verdeckt wird.