A - Hilfsmittelfreier Teil

Analysis - Niveau 1

Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f: x\mapsto x^4-4 x^3.$

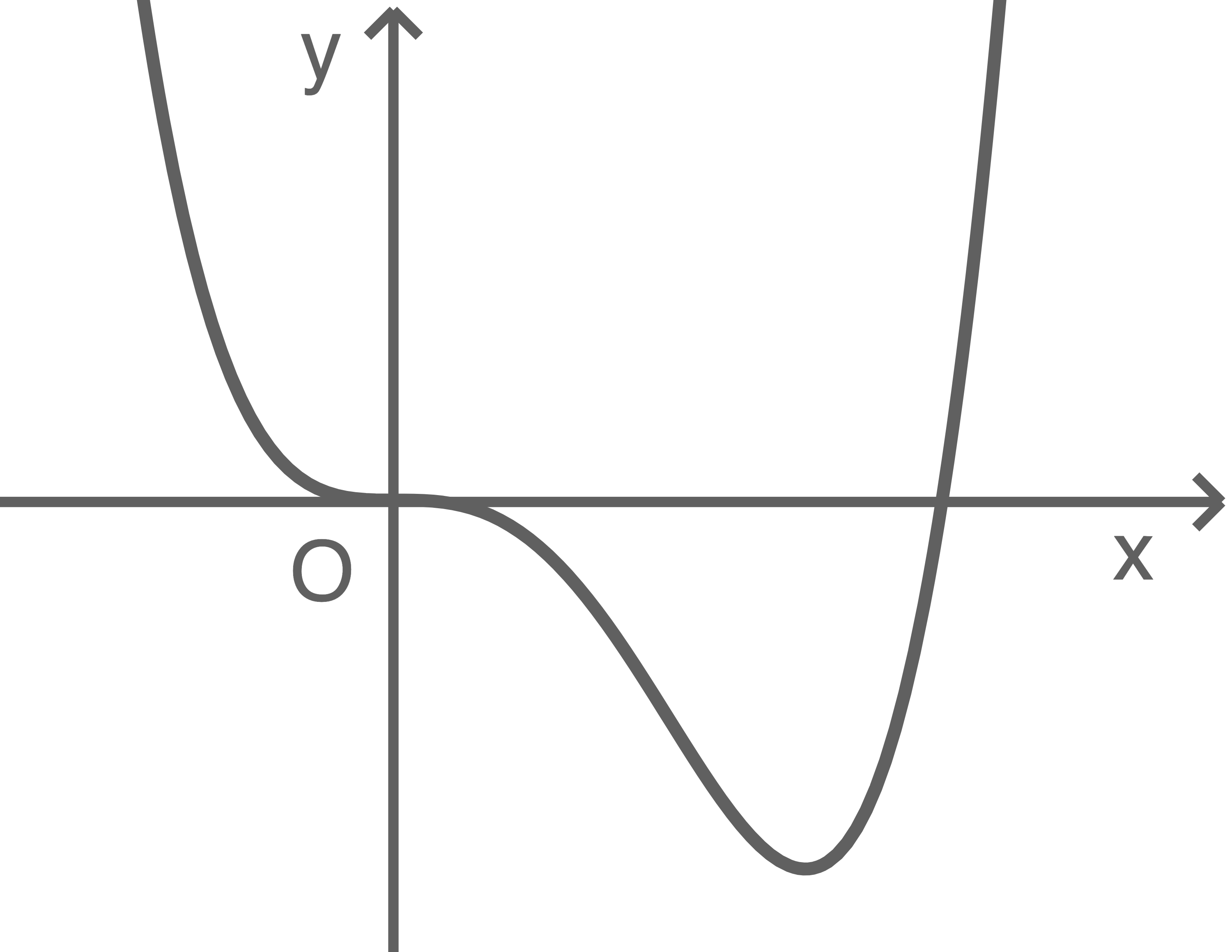
1.1

Berechne den Wert des Integrals $\displaystyle\int_{0}^{1}f(x)\;\mathrm dx.$

(2 BE)

1.2

Beurteile, ob die folgende Aussage richtig ist:

Für die Abbildung wurde eine Längeneinheit auf der $x$ -Achse ebenso groß gewählt wie auf der $y$ -Achse.

(1 BE)

Lineare Algebra/ Analytische Geometrie - Niveau 1

Gegeben sind die Gerade $g: \overrightarrow{x}=\pmatrix{2\\3\\-7}+s\cdot\pmatrix{1\\0\\5}$ mit $\mathrm{s} \in \mathbb{R}$ sowie die Gerade $h$ durch die Punkte $A(4\mid0\mid 0)$ und $B(5\mid1\mid b)$ mit einer reellen Zahl $b.$

2.1

Begründe, dass $A$ nicht auf $g$ liegt.

(1 BE)

2.2

Die Geraden $g$ und $h$ haben einen gemeinsamen Punkt.

Ermittle den Wert von $b.$

(4 BE)

Stochastik - Niveau 1

In einer Grundschule sind 60 Mädchen und 40 Jungen. Bei einer Befragung aller Mädchen und Jungen geben von den Mädchen 50 an, gerne Ballspiele im Sportunterricht zu spielen. Von den Jungen geben 5 an, nicht gerne Ballspiele im Sportunterricht zu spielen.

Betrachtet werden die Ereignisse:

$M:$ Das befragte Kind ist ein Mädchen.

$B:$ Das befragte Kind gibt an, gerne Ballspiele im Sportunterricht zu spielen.

3.1

Stelle den Sachverhalt in einer Vierfeldertafel dar.

(3 BE)

3.2

Zeige, dass $P_M(B)\lt P_{\overline{M}}(B)$ gilt.

(2 BE)

Stochastik - Niveau 2

Zwei Tetraeder, deren vier Seiten jeweils mit den Zahlen 1 bis 4 beschriftet sind, werden geworfen (Abbildung).

Betrachtet werden die Ereignisse:

$A:$ Die Summe der Augenzahlen ist gerade.

$B:$ Das Produkt der Augenzahlen ist größer als 4.

Tetraeder Wahrscheinlichkeiten Hessen Mathe Abi 2023

4.1

Bestimme die folgenden Wahrscheinlichkeiten:

$P(A), P(B)$ und $P(A \cap B)$

(3 BE)

4.2

Zeige, dass für die Wahrscheinlichkeit $P(A \cup B)$ der oben genannten Ereignisse $A$ und $B$ die Formel $P(A \cup B)=P(A) + P(B) -P(A \cap B)$ gilt.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Analysis - Niveau 1

1.1

$\displaystyle\int_{0}^{1}f(x)\;\mathrm dx= -\dfrac{4}{5} \; [\text{FE}]$

Rechenweg anzeigen

1.2

$\begin{array}[t]{rll} f(x)&=& 0& \\[5pt] x^4-4\cdot x^3&=& 0& \\[5pt] x^3\cdot (x-4)&=& 0& \\[5pt] \end{array}$

Die Nullstellen folgen also mit $x_1=0$ und $x_2=4.$

Durch Einsetzen eines beliebigen $x$ -Wertes kann die Aussage überprüft werden:

$f(3)=3^4-4\cdot 3^3=-27$

Der Punkt des Graphen mit der $x$ -Koordinate 3 liegt nicht neunmal so weit von der $x$ -Achse entfernt wie von der $y$ -Achse.

Somit ist die Aussage falsch.

Lineare Algebra/ Analytische Geometrie - Niveau 1

2.1

Alle Punkte auf $g$ haben die $y$ -Koordinate $3,$ $A$ hat allerdings die $y$ -Koordinate $0.$

Somit liegt $A$ nicht auf $g.$

2.2

1. Schritt: Gleichung von $h$ aufstellen

$\begin{array}[t]{rll} h: \overrightarrow{x}&=& \overrightarrow{OA}+t\cdot \overrightarrow{AB}& \\[5pt] &=& \pmatrix{4\\0\\0}+t\cdot\pmatrix{1\\1\\b} \end{array}$

2. Schritt: Gleichsetzen von $g$ und $h$

$\pmatrix{2+s\\3\\-7+5s}= \pmatrix{4+t\\t\\t\cdot b}$

Rechenweg anzeigen

Aus der zweiten Zeile folgt $t=3.$

Einsetzen in die erste Zeile liefert:

$\begin{array}[t]{rll} 2+s&=& 4+3 &\quad \scriptsize \mid\; -2 \\[5pt] s&=& 5 \end{array}$

Mit $t=3$ und $s=5$ folgt für die dritte Zeile somit:

$\begin{array}[t]{rll} -7+5\cdot 5&=& 3\cdot b&\\[5pt] 18&=& 3\cdot b&\quad \scriptsize \mid\; :3 \\[5pt] 6&=& b \end{array}$

Stochastik - Niveau 1

3.1

	$\color{#fff}{M}$	$\color{#fff}{\overline{M}}$	Gesamt
$\color{#fff}{B}$	$50$	$35$	$85$
$\color{#fff}{\overline{B}}$	$10$	$5$	$15$
Gesamt	$60$	$40$	$100$

3.2

Für die bedingten Wahrscheinlichkeiten ergibt sich:

$\begin{array}[t]{rll} P_M(B)&=& \dfrac{50}{60}& \\[5pt] &\approx& 0,833 & \\[5pt] &=& 83,3 \,\% \end{array}$

$\begin{array}[t]{rll} P_{\overline{M}}(B)&=& \dfrac{35}{40}& \\[5pt] &=& 0,875 & \\[5pt] &=& 87,5 \,\% \end{array}$

Stochastik - Niveau 2

4.1

Wahrscheinlichkeit $\boldsymbol{P(A)}$

Für das Ereignis $A$ gibt es folgende acht Möglichkeiten:

$(1,1),$ $(1,3),$ $(2,2),$ $(2,4),$ $(3,1),$ $(3,3),$ $(4,2),$ $(4,4)$

Für beide Tetraeder beträgt die Wahrscheinlichkeit für jede der vier Zahlen jeweils $\dfrac{1}{4}.$

Somit folgt:

$P(A)= 8\cdot \dfrac{1}{4}\cdot \dfrac{1}{4} = \dfrac{1}{2}$

Wahrscheinlichkeit $\boldsymbol{P(B)}$

Für das Ereignis $B$ gibt es folgende acht Möglichkeiten:

$(2,3),$ $(2,4),$ $(3,2),$ $(3,3),$ $(3,4),$ $(4,2),$ $(4,3),$ $(4,4)$

Analog zu Ereignis $A$ folgt also:

$P(B)= 8\cdot \dfrac{1}{4}\cdot \dfrac{1}{4} = \dfrac{1}{2}$

Wahrscheinlichkeit $\boldsymbol{P(A \cap B)}$

Die vier Wurfpaare $(2,4), (3,3), (4,2), (4,4)$ sind sowohl in Ereignis $A$ als auch in Ereignis $B$ enthalten.

Es ergibt sich also:

$P(A \cap B)= 4\cdot \dfrac{1}{4}\cdot \dfrac{1}{4} = \dfrac{1}{4}$

4.2

Für das Ereignis $A \cup B$ gibt es die folgenden 12 Wurfmöglichkeiten:

$(1,1),$ $(1,3),$ $(2,2),$ $(2,3),$ $(2,4),$ $(3,1),$ $(3,2),$ $(3,3),$ $(3,4),$ $(4,2),$ $(4,3),$ $(4,4)$

Es folgt somit:

$P(A \cup B)=12\cdot \dfrac{1}{4}\cdot \dfrac{1}{4}= \dfrac{3}{4}$

Einsetzen in die Formel aus der Aufgabenstellung liefert:

Rechenweg anzeigen

$\dfrac{3}{4} = \dfrac{3}{4}$

Somit gilt für die Wahrscheinlichkeit $P(A \cup B)$ die Formel $P(A \cup B)= P(A)+P(B)-P(A\cap B).$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?