B2 - Analytische Geometrie

Auf dem Rollfeld eines Flughafens steht ein Flugzeug vom Typ Cessna. Für eine mathematische Betrachtung wird diese Situation in einem Koordinatensystem dargestellt:

Die Längsachse des Flugzeugs verläuft parallel zur $x$ -Achse. Der linke und der rechte Flugzeugflügel sind symmetrisch zur $x$ - $z$ -Ebene angeordnet. Die Punkte $A(1\mid1\mid1), B(0\mid7\mid2), C(-1\mid7\mid2)$ und $D(-2\mid1\mid1)$ bilden die Eckpunkte der Oberseite des linken Flugzeugflügels (Material 1 und 2). Das Rollfeld liegt in der $x$ - $y$ -Ebene.

Eine Einheit entspricht einem Meter.

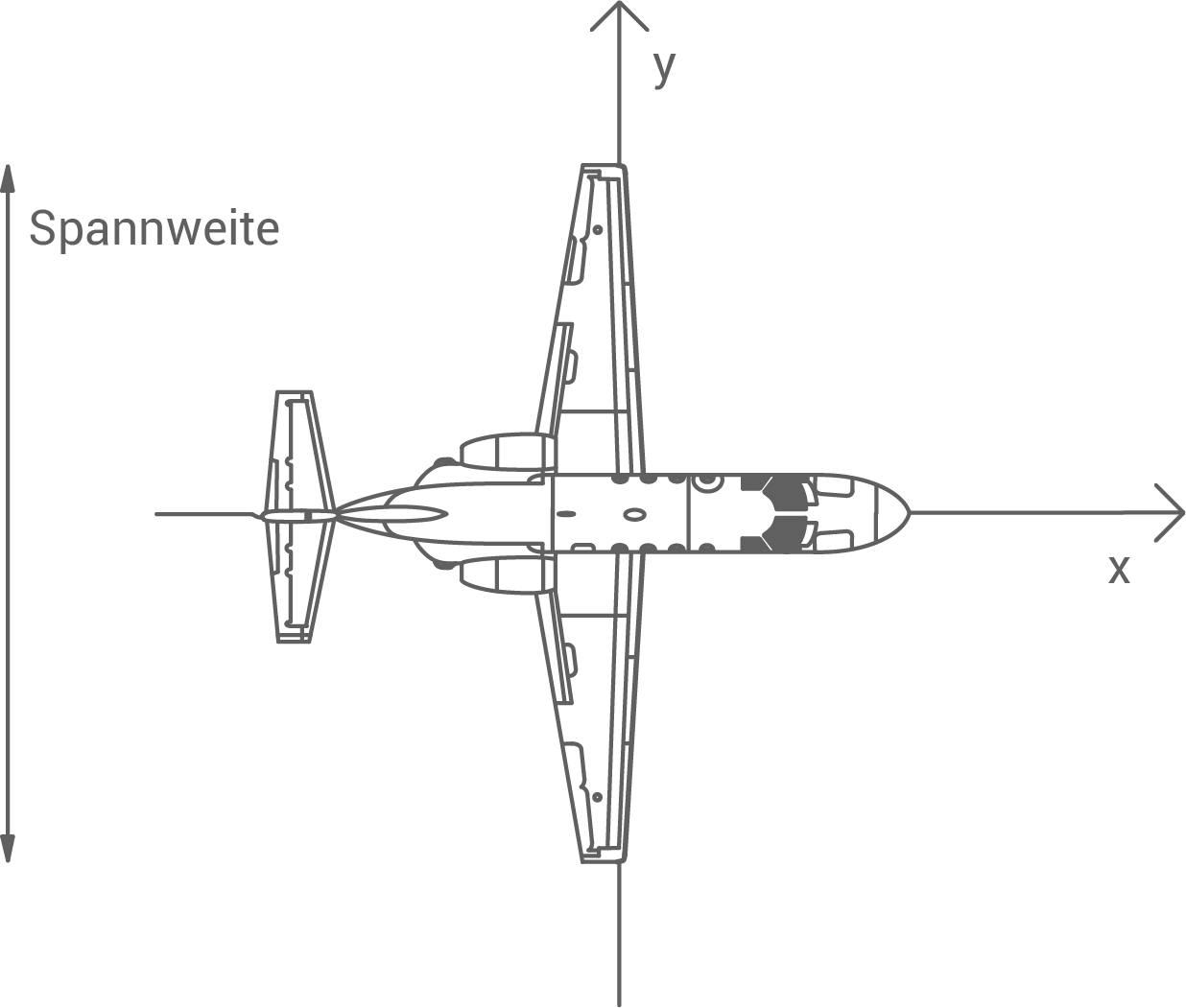
B2 - Analytische Geometrie Zeichnung Cessna

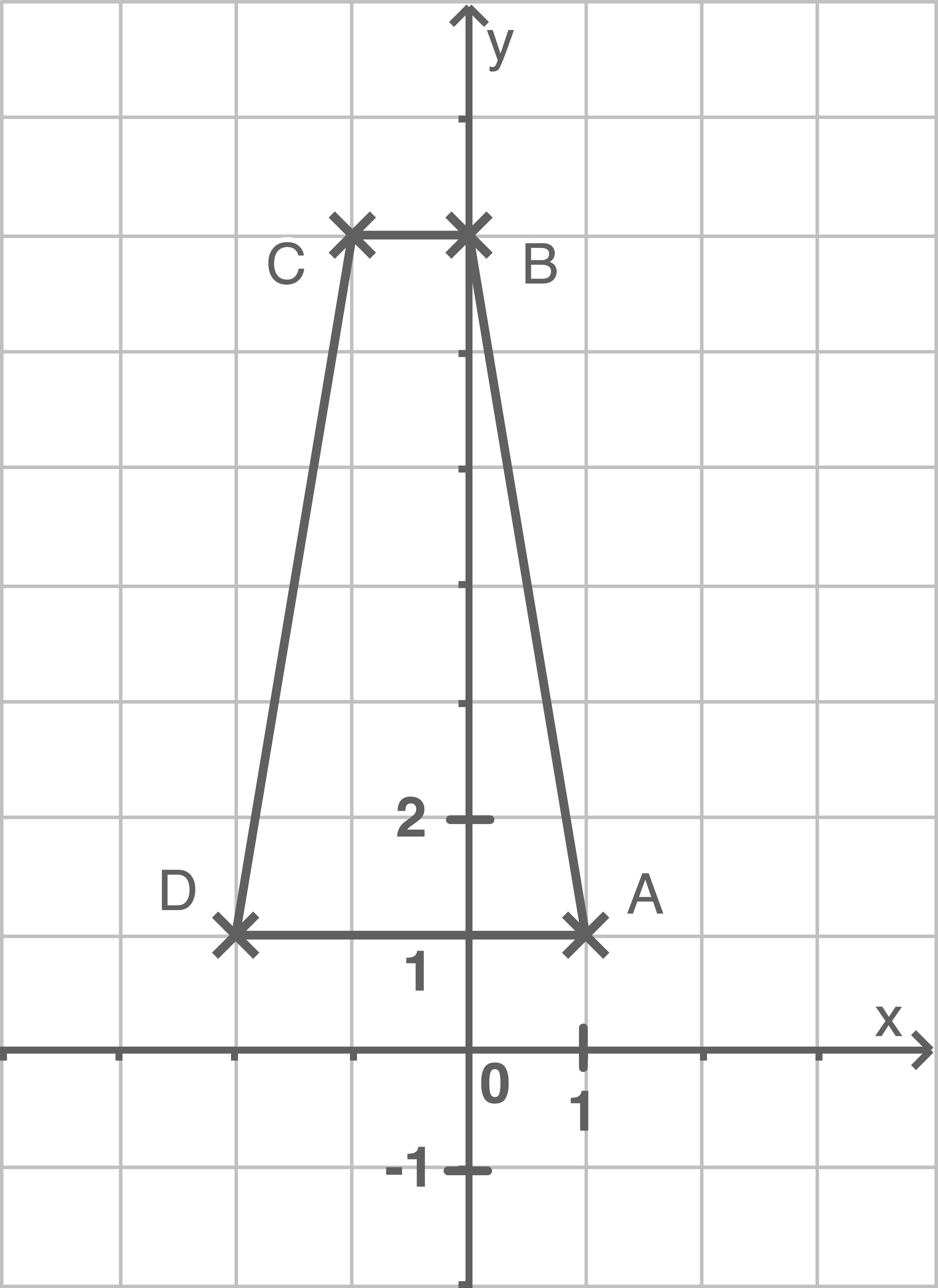
Abb.1: Flugzeug vom Typ Cessna von oben gesehen (die $z$ -Achse zeigt direkt auf den Betrachter zu)

B2 - Analytische Geometrie Flugzeugflügel

Abb.2: Idealisierte Skizze des linken Flugzeugflügels von oben gesehen (die $z$ -Achse zeigt direkt auf den Betrachter zu)

1.1

Die durch die Eckpunkte $A, B, C$ und $D$ gegebene Oberseite des linken Flugzeugflügels liegt in einer Ebene $E.$ Gib eine Parametergleichung dieser Ebene an.

(3 BE)

1.2

Eine mögliche Koordinatengleichung der Ebene $E$ lautet $E: y-6z = -5.$

Bestimme den Neigungswinkel der Ebene $E$ gegenüber der Ebene des Rollfelds.

(3 BE)

1.3

Begründe unter Angabe einer Rechnung, dass die durch die Punkte $A, B, C$ und $D$ beschriebene Oberseite des Flugzeugflügels trapezförmig ist.

(2 BE)

Die Koordinaten der Eckpunkte der Oberseite des rechten Flugzeugflügels erhält man durch Spiegelung von $A, B, C$ und $D$ an der $x$ - $z$ -Ebene.

Gib die Koordinaten der Spiegelpunkte $\(A$ und $\(D$ an und bestimme den größtmöglichen Abstand zwischen zwei einander gegenüberliegenden Eckpunkten der Flugzeugflügel, die sogenannte Spannweite der Cessna.

(4 BE)

Die Größe der Oberfläche des linken Flugzeugflügels soll berechnet werden.
Erläutere hierzu die im Kasten dargestellte Vorgehensweise in den Zeilen $\text{(I)}$ bis $\text{(V)}$ und deute die Zeile $\text{(V)}$ im Sachzusammenhang.
Gib in den Zeilen $\text{(III)}$ und $\text{(V)}$ die durch Auslassungspunkte gekennzeichneten fehlenden Berechnungen an.

$\text{(I)}$

$g:\, \overrightarrow{x}$ $= \pmatrix{1\\1\\1} +r\cdot \pmatrix{-3\\0\\0}$

$\text{(II)}$

$\left(\pmatrix{1\\1\\1} +r\cdot \pmatrix{-3\\0\\0}-\pmatrix{0\\7\\2} \right) \cdot \pmatrix{-3\\0\\0} = 0$

$\text{(III)}$

$... \Leftrightarrow r = \frac{1}{3}$

Einsetzen von $r$ in $g$ liefert $F(0\mid1\mid1).$

$\text{(IV)}$

$h_T= \,\bigg \vert \,\overrightarrow{BF}\,\bigg \vert \, \approx 6,08$

$\text{(V)}$

$A_T = \dfrac{1}{2}\cdot \left(\,\bigg \vert \, \overrightarrow{AD}\,\bigg \vert \, + \,\bigg \vert \,\overrightarrow{BC} \,\bigg \vert \, \right) \cdot \,\bigg \vert \,\overrightarrow{BF} \,\bigg \vert \, \approx ...$

(9 BE)

Die Oberseite der Flugzeugflügel soll mit einer Aluminiumlegierung versehen werden. Sie besteht aus $80\,\%$ Aluminium, $6\,\%$ Zink und $14\,\%$ sonstigen Bestandteilen. Gemischt werden soll diese Aluminiumlegierung aus drei Grundstoffen $G1, G2$ und $G3,$ die die in der Tabelle dargestellten Anteile an Aluminium, Zink und den sonstigen Bestandteilen besitzen.

	$\color{#fff}{G1}$	$\color{#fff}{G2}$	$\color{#fff}{G3}$
Aluminiumanteil (in $\color{#fff}{\,\%}$ )	$60$	$90$	$92$
Zinkanteil (in $\color{#fff}{\,\%}$ )	$10$	$5$	$2$
sonstige Bestandteile (in $\color{#fff}{\,\%}$ )	$30$	$5$	$6$

Um zu prüfen, ob die gewünschte Aluminiumlegierung aus den Grundstoffen $G1,$ $G2$ und $G3$ hergestellt werden kann, wird folgendes lineares Gleichungssystem erstellt:

$\begin{array}{llll} \text{I}\quad & 60x+90y+92z &=& 80 \\ \text{II}\quad & 10x+5y+2z &=& 6 \\ \text{III}\quad & 30x+5y+6z &=& 14 \\ \end{array}$

4.1

Erläutere die Bedeutung der Gleichung $\text{II}$ im Sachzusammenhang.

(3 BE)

4.2

Berechne die Lösung des linearen Gleichungssystems und deute das Ergebnis im Sachzusammenhang.

(6 BE)

1.1

Eine mögliche Parametergleichung der Ebene ergibt sich wie folgt:

Rechenweg anzeigen

$E:\,\overrightarrow{x} = ...$

1.2

Da das Rollfeld in der $x$ - $y$ -Ebene liegt, folgt als ein Normalenvektor $\overrightarrow{n}_1 = \pmatrix{0\\0\\1}.$

Für $E$ folgt aus der Koordinatengleichung: $\overrightarrow{n}_2 = \pmatrix{0\\1\\-6}.$

Es folgt:

Rechenweg anzeigen

$\alpha \approx 9,46^{\circ}$

Der Neigungswinkel von $E$ gegenüber der Ebene des Rollfelds beträgt ca. $9,46^{\circ}.$

1.3

Bei einem Trapez müssen zwei gegenüberliegende Seiten zueinander parallel sein.

Für $\overrightarrow{AD} = \pmatrix{-3\\0\\0}$ und $\overrightarrow{BC} = \pmatrix{-1\\0\\0}$ gilt $\overrightarrow{AD} = 3\cdot \overrightarrow{BC}.$

Somit sind auch die zugehörigen Seiten des Vierecks parallel und es handelt sich bei dem Viereck $ABCD,$ der Oberseite des Flugzeugflügels, um ein Trapez.

Koordinaten der Spiegelpunkte angeben

Eine Spiegelung an der $x$ - $z$ -Ebene ergibt sich durch das Umkehren der Vorzeichen der $y$ -Koordinaten. Für die Spiegelpunkte folgt:

$\( A$ $\( B$ $\( C$ $\( D$

Spannweite bestimmen

Die Vektoren $\overrightarrow{AD}$ und $\overrightarrow{BC}$ sind parallel zur $x$ - $z$ -Ebene und parallel zur $x$ -Achse.
Die Spannweite entspricht daher dem Abstand der beiden Punkte $B$ und $\( B$ bzw. $C$ und $\( C$ Mit Hilfe des norm-Befehls des CAS folgt für den Vektorbetrag:

$\left|\overrightarrow{BB‘}\right|$ $= \left|\pmatrix{0\\14\\0}\right|$ $= \sqrt{0^2+14^2+0^2} = 14$

Die Spannweite des Flugzeugs beträgt $14\,\text{m}.$

Vorgehensweise erläutern

$\text{(I)}$

Aufstellung einer Geraden $g,$ die durch die Punkte $A$ und $D$ verläuft.

$\text{(II)}$

Es wird zunächst eine Ebenengleichung in Normalform aufgestellt, mit Normalenvektor $\overrightarrow{AD}$ und Stützpunkt $B.$
In diese Ebenengleichung werden die Koordinaten der Punkte der Geraden $g$ eingesetzt um den Schnittpunkt der Geraden und der Ebene zu bestimmen.
Dieser ist der Punkt auf $g$ mit dem kürzesten Abstand zu $B.$

$\text{(III)}$

Die Gleichung aus $\text{(II)}$ wird nach $r$ aufgelöst und in die Gleichung von $g$ eingesetzt. Der Punkt $F(0\mid 1\mid 1)$ ist somit der Punkt auf der Strecke $\overline{AD}$ mit dem kürzesten Abstand zu $B.$

$\text{(IV)}$

Die Höhe des Trapezes $ABCD$ entspricht dem Abstand des Punktes $B$ zur Geraden $g.$ Die Höhe kann daher über den Vektorbetrag des Verbindungsvektors von $B$ und $F$ berechnet werden und beträgt ca. $6,08\;\text{[LE]}.$

$\text{(V)}$

Mit Hilfe der in $\text{(IV)}$ berechneten Höhe des Trapezes und des Betrages der parallelen Trapezseiten $\overline{AD}$ und $\overline{BC}$ wird der Flächeninhalt des Trapezes berechnet, welches die Oberfläche des Flugzeugflügels beschreibt.

Fehlende Berechnungen angeben

$\text{(III)}$

Rechenweg anzeigen

$r =\dfrac{1}{3}$

$\text{(V)}$

Rechenweg anzeigen

$A_T \approx 12,16 \;[\text{m}^2]$

4.1

In Gleichung $\text{II}$ wird der Zinkanteil in der Zusammensetzung aus $x$ Teilen des Grundstoffes $G1,$ $y$ Teilen des Grundstoffes $G2$ und $z$ Teilen des Grundstoffes $G3$ mit dem geforderten Anteil des Zinks in der Aluminiumlegierung in Prozent gleichgesetzt.

4.2

Rechenweg anzeigen

$y = 0,4$

Einsetzen von $y$ in die ersten beiden Gleichungen liefert:

Rechenweg anzeigen

$z= 0,25$

Einsetzen von $z$ in $\text{II}$ liefert nun:

Rechenweg anzeigen

$x = 0,35$

Die Lösung des linearen Gleichungssystems ist somit $x= 0,35,$ $y=0,4$ und $z=0,25.$ Die Aluminiumlegierung muss also aus $35\,\%$ von $G1,$ $40\,\%$ von $G2$ und $25\,\%$ von $G3$ bestehen.