A1 - Analysis

Berechne die erste Ableitung der Funktion und ermittle damit unter Zuhilfenahme der zweiten Ableitung die Extrem- und Wendepunkte des Graphen von innerhalb des betrachteten Intervalls ohne Verwendung des Graphen.
Begründe das Grenzwertverhalten des Graphen für anhand des Funktionsterms von

Bestimme, zu welchen Zeiten die Population größer als 100.000 Käfer ist und wie stark die Population in den ersten 6 Jahren durchschnittlich pro Jahr zunimmt.

Beschreibe unter Verwendung der Begriffe „Populationsgröße“ und „Wachstumgsgeschwindigkeit“ die Entwicklung der Käferpopulation. Deute dabei sowohl die Extrem- und Wendepunkte als auch den Grenzwert des Graphen aus Aufgabe 1.

Zeige, dass mit eine Stammfunktion von ist. Berechne den Wert von und deute diesen im Sachzusammenhang.

Die Funktion beschreibt die Entwicklung der Käferpopulation nur für die ersten 55 Jahre recht gut. Ab dem Zeitpunkt bleibt bei einer verbesserten Beschreibung die zu diesem Zeitpunkt erreichte Wachstumgsgeschwindigkeit konstant, sodass für ein lineares Wachstum vorliegt.
Ermittle die momentane Wachstumsgeschwindigkeit bei und bestimme mit Hilfe der Funktionsgleichung, die ab diesem Punkt die Populationsgröße beschreibt, den voraussichtlichen Zeitpunkt des Aussterbens der Käferpopulation.

Extrempunkte bestimmen Mit Hilfe des CAS folgt für die erste Abbildung: 1. Schritt: Notwendiges Kriterium für Extremstellen anwenden Definition der Ableitung von im Taschenrechner liefert mit Hilfe dem solve-Befehl des CAS als mögliche Extremstelle: 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen Mit Hilfe der zweiten Ableitung von aus auf der Aufgabenstellung und dem solve-Befehl folgt: Da gilt, hat also an der Stelle einen Hochpunkt mit den Koordinaten Wendepunkte bestimmen 1. Schritt: Notwendige Bedingung für Extremstellen anwenden Nullsetzen der zweiten Ableitung liefert mit Hilfe des solve-Befehls des CAS: 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen Definition der dritten Ableitung im CAS liefert an der Stelle Die Funktion hat damit eine Wendestelle mit den Koordinaten Grenzwertverhalten begründen Das Grenzwertverhalten der einzelnen Komponenten des Funktionsterms ist wie folgt: besitzt lineares Wachstum und es gilt besitzt exponentielles Wachstum und es gilt Da exponentielles Wachstum stärker als lineares Wachstum ist, folgt für das Grenzwertverhalten des Funktionsterms von .

Zeiten bestimmen Mit Hilfe der Berechnung der Stellen, an denen die Größer der Population genau Käfer beträgt, lässt sich bestimmen in welchen Zeiten die Population größer als ist. Da eine Einheit Käfer beträgt,folgt mit Hilfe des solve-Befehls des CAS auf die Gleichung Da der Hochpunkt der Funktion bei liegt, ist die Käferpopulation für größer als Käfer. Durchschnittliche Zunahme der Population berechnen Mit Hilfe der Funktionswerte an den Stellen und folgt mit dem CAS für die momentane Änderungsrate: In den ersten Jahren nimmt die Population somit also durchschnittlich Käfer pro Jahr zu.

In dem CAS können die beiden folgenden Graphen graphisch gegeneinander aufgetragen werden: 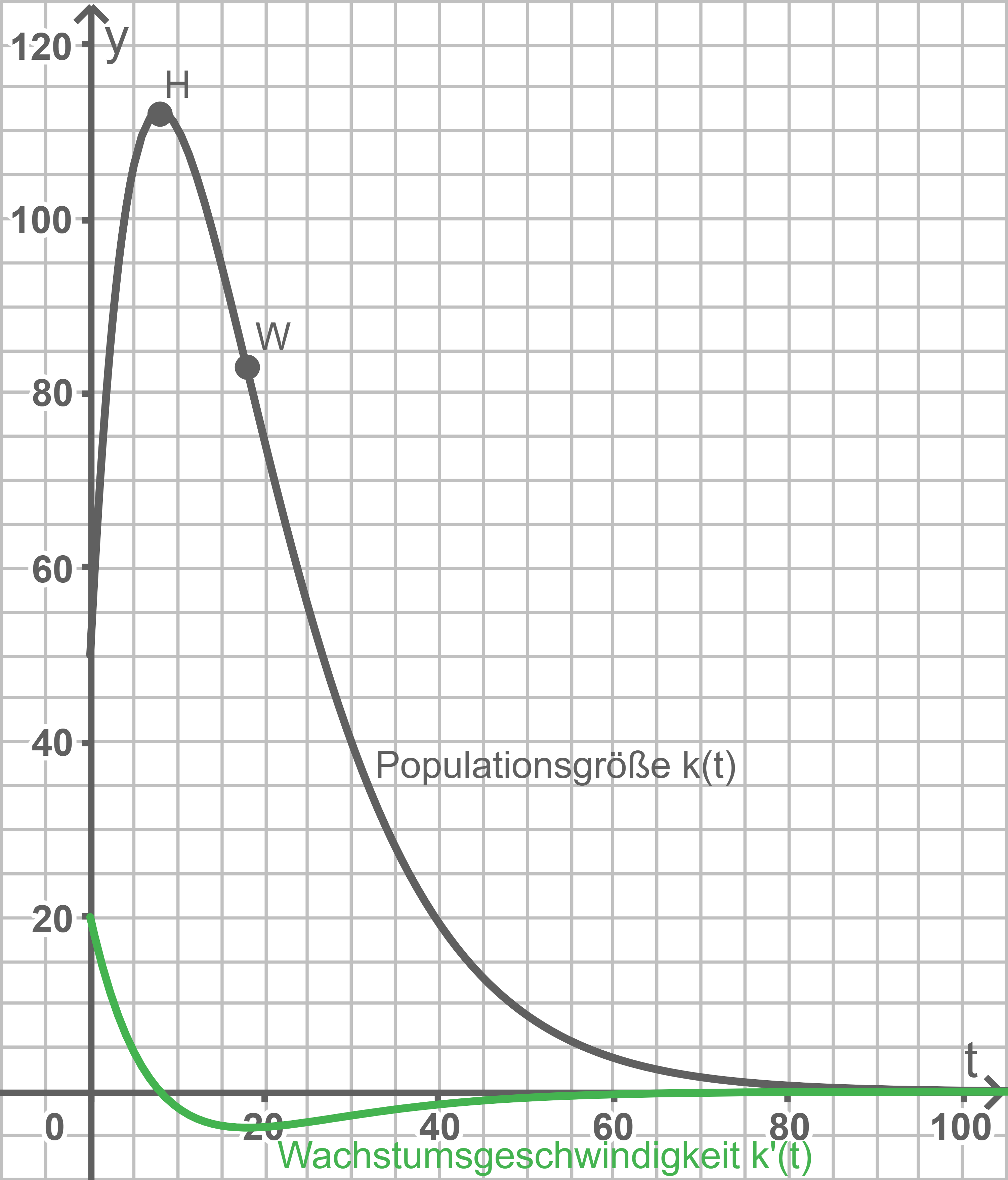Der Anfangsbestand der Käferpopulation beträgt wegen gerade Käfer. Bis zum Hochpunkt in dem die Populationsgröße mit Käfern ihren maximalen Wert erreicht, wächst die Population, da die Wachstumsgeschwindigkeit bis dahin positiv ist. An dem Graphen von kann abgelesen werden, dass die Käferpopulation nach dem Hochpunkt abnimmt. Dies kannst mit der negativen Wachstumsgeschwindigkeit erklärt werden. Im Wendepunkt beträgt die Populationgröße Käfer. Da an der Stelle einen Tiefpunkt besitzt, wird die Populationsgröße hier am stärksten dezimiert, die Wachstumsgeschwindigkeit ist minimal. Da gilt, nähert sich die Populationsgröße im Laufe der Zeit immer näher der an, d.h. die Käferpopulation stirbt langsam aus. Die Wachstumsgeschwindigkeit bleibt im Intervall also negativ, wobei ihr Betrag immer kleiner wird.

Stammfunktion nachweisen Mit Hilfe der Produkt- und Kettenregel folgt für die Ableitung von Damit ist eine Stammfunktion von . Integral berechnen Mit Hilfe des CAS wird das Integral wie folgt berechnet: 4: Analysis 3: Integral Es folgt: Integral im Sachzusammenhang deuten Der Ausdruck gibt den durchschnittlichen Funktionswert des Graphen von zwischen und an. Da eine Einheit der Funktionswerte Käfern entspricht, liefert die durchschnittliche Anzahl der Käfer zwischen Jahr und

Momentane Wachstumsgeschwindigkeit berechnen Für die momentane Wachstumsgeschwindigkeit bei folgt durch Einsetzen in Neue Funktionsgleichung bestimmen Da ab der Stelle ein lineares Wachstum für die Käferpopulation angenommen wird, beschreibt die Tangente mit allgemeiner Form an den Graphen von an der Stelle den weiteren Verlauf.
Die Tangente die besitzt die Steigung , da dies die momentane Wachstumsgeschwindigkeit an der Stelle ist. Somit gilt .
Da die Tangente und die Funktion an der Stelle denselben -Wert besitzen, folgt für Voraussichtlichen Zeitpunkt des Aussterbens der Käferpopulation berechnen Nullsetzen von liefert mit Hilfe des solve-Befehls des CAS als Nullstelle: Der voraussichtliche Zeitpunkt des Aussterbens der Käferpopulation beträgt damit ca.

Extrempunkte bestimmen Mit Hilfe des CAS folgt für die erste Abbildung: 1. Schritt: Notwendiges Kriterium für Extremstellen anwenden Definition der Ableitung von im Taschenrechner liefert mit Hilfe dem solve-Befehl des CAS als mögliche Extremstelle: 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen Mit Hilfe der zweiten Ableitung von aus auf der Aufgabenstellung und dem solve-Befehl folgt: Da gilt, hat also an der Stelle einen Hochpunkt mit den Koordinaten Wendepunkte bestimmen 1. Schritt: Notwendige Bedingung für Extremstellen anwenden Nullsetzen der zweiten Ableitung liefert mit Hilfe des solve-Befehls des CAS: 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen Definition der dritten Ableitung im CAS liefert an der Stelle Die Funktion hat damit eine Wendestelle mit den Koordinaten Grenzwertverhalten begründen Das Grenzwertverhalten der einzelnen Komponenten des Funktionsterms ist wie folgt: besitzt lineares Wachstum und es gilt besitzt exponentielles Wachstum und es gilt Da exponentielles Wachstum stärker als lineares Wachstum ist, folgt für das Grenzwertverhalten des Funktionsterms von .

Zeiten bestimmen Mit Hilfe der Berechnung der Stellen, an denen die Größer der Population genau Käfer beträgt, lässt sich bestimmen in welchen Zeiten die Population größer als ist. Da eine Einheit Käfer beträgt,folgt mit Hilfe des solve-Befehls des CAS auf die Gleichung Da der Hochpunkt der Funktion bei liegt, ist die Käferpopulation für größer als Käfer. Durchschnittliche Zunahme der Population berechnen Mit Hilfe der Funktionswerte an den Stellen und folgt mit dem CAS für die momentane Änderungsrate: In den ersten Jahren nimmt die Population somit also durchschnittlich Käfer pro Jahr zu.

In dem CAS können die beiden folgenden Graphen graphisch gegeneinander aufgetragen werden: Der Anfangsbestand der Käferpopulation beträgt wegen gerade Käfer. Bis zum Hochpunkt in dem die Populationsgröße mit Käfern ihren maximalen Wert erreicht, wächst die Population, da die Wachstumsgeschwindigkeit bis dahin positiv ist. An dem Graphen von kann abgelesen werden, dass die Käferpopulation nach dem Hochpunkt abnimmt. Dies kannst mit der negativen Wachstumsgeschwindigkeit erklärt werden. Im Wendepunkt beträgt die Populationgröße Käfer. Da an der Stelle einen Tiefpunkt besitzt, wird die Populationsgröße hier am stärksten dezimiert, die Wachstumsgeschwindigkeit ist minimal. Da gilt, nähert sich die Populationsgröße im Laufe der Zeit immer näher der an, d.h. die Käferpopulation stirbt langsam aus. Die Wachstumsgeschwindigkeit bleibt im Intervall also negativ, wobei ihr Betrag immer kleiner wird.

Stammfunktion nachweisen Mit Hilfe der Produkt- und Kettenregel folgt für die Ableitung von Damit ist eine Stammfunktion von . Integral berechnen Mit Hilfe des CAS wird das Integral wie folgt berechnet: Interactive Calculation Es folgt: Integral im Sachzusammenhang deuten Der Ausdruck gibt den durchschnittlichen Funktionswert des Graphen von zwischen und an. Da eine Einheit der Funktionswerte Käfern entspricht, liefert die durchschnittliche Anzahl der Käfer zwischen Jahr und

Momentane Wachstumsgeschwindigkeit berechnen Für die momentane Wachstumsgeschwindigkeit bei folgt durch Einsetzen in Neue Funktionsgleichung bestimmen Da ab der Stelle ein lineares Wachstum für die Käferpopulation angenommen wird, beschreibt die Tangente mit allgemeiner Form an den Graphen von an der Stelle den weiteren Verlauf.
Die Tangente die besitzt die Steigung , da dies die momentane Wachstumsgeschwindigkeit an der Stelle ist. Somit gilt .
Da die Tangente und die Funktion an der Stelle denselben -Wert besitzen, folgt für Voraussichtlichen Zeitpunkt des Aussterbens der Käferpopulation berechnen Nullsetzen von liefert mit Hilfe des solve-Befehls des CAS als Nullstelle: Der voraussichtliche Zeitpunkt des Aussterbens der Käferpopulation beträgt damit ca.