B2 - Analysis
Bei der Dampfpfeife handelt es sich um eine technische Vorrichtung, bei der durch hochkomprimierten Wasserdampf ein akustisches Signal erzeugt wird. Dampfpfeifen werden beispielsweise bei Dampfschiffen oder Dampflokomotiven eingesetzt. Über eine Änderung der Dosierung des durchströmenden Wasserdampfs können unterschiedliche Pfeifsignale erzeugt werden.
Zur Untersuchung verschieden erzeugter Pfeifsignale kann mithilfe einer speziellen Messvorrichtung der sogenannte Wasserdampfstrom bestimmt werden. Darunter versteht man das Volumen des ausströmenden Wasserdampfs pro Zeiteinheit.
Die im Folgenden verwendeten Funktionen ,
,  und
und  sowie die Funktionenschar
sowie die Funktionenschar  modellieren jeweils den gemessenen Wasserdampfstrom für unterschiedliche Pfeifsignale. Hierbei gibt
modellieren jeweils den gemessenen Wasserdampfstrom für unterschiedliche Pfeifsignale. Hierbei gibt  die Zeit in Sekunden seit Beobachtungsbeginn an; die Funktionswerte beschreiben den Wasserdampfstrom in
die Zeit in Sekunden seit Beobachtungsbeginn an; die Funktionswerte beschreiben den Wasserdampfstrom in 
 .
.
 mit
mit  ,
,  , im Intervall
, im Intervall ![\(I=[0;2,6]\)](https://mathjax.schullv.de/b7b934106f4dfc221b7d200c26393a6896e22e9e7087a515dc246a343ef06c7d?color=5a5a5a) .
.
 Sekunden kann durch die Funktion
Sekunden kann durch die Funktion  modelliert werden. Für
modelliert werden. Für  und
und  gilt im Intervall
gilt im Intervall ![\([0;2,65]\)](https://mathjax.schullv.de/480fc6382f5b056b2fd7c08f10c91e258fc6ef3f8257f9c2effb6a22267e14cc?color=5a5a5a) :
:
 und
und 
Zur Untersuchung verschieden erzeugter Pfeifsignale kann mithilfe einer speziellen Messvorrichtung der sogenannte Wasserdampfstrom bestimmt werden. Darunter versteht man das Volumen des ausströmenden Wasserdampfs pro Zeiteinheit.
Die im Folgenden verwendeten Funktionen
1
In der Abbildung sind der Graph der Funktion  im Intervall
im Intervall ![\([0;3,5]\)](https://mathjax.schullv.de/f9a140cadabb078a37e5f7103b445aa9ccd3bce63100a880c7ebdb68c1ef14a1?color=5a5a5a) sowie die hellgrünen Rechtecke der Obersumme
sowie die hellgrünen Rechtecke der Obersumme  und ein dunkelgrünes Rechteck der Untersumme
und ein dunkelgrünes Rechteck der Untersumme  dargestellt.
dargestellt.
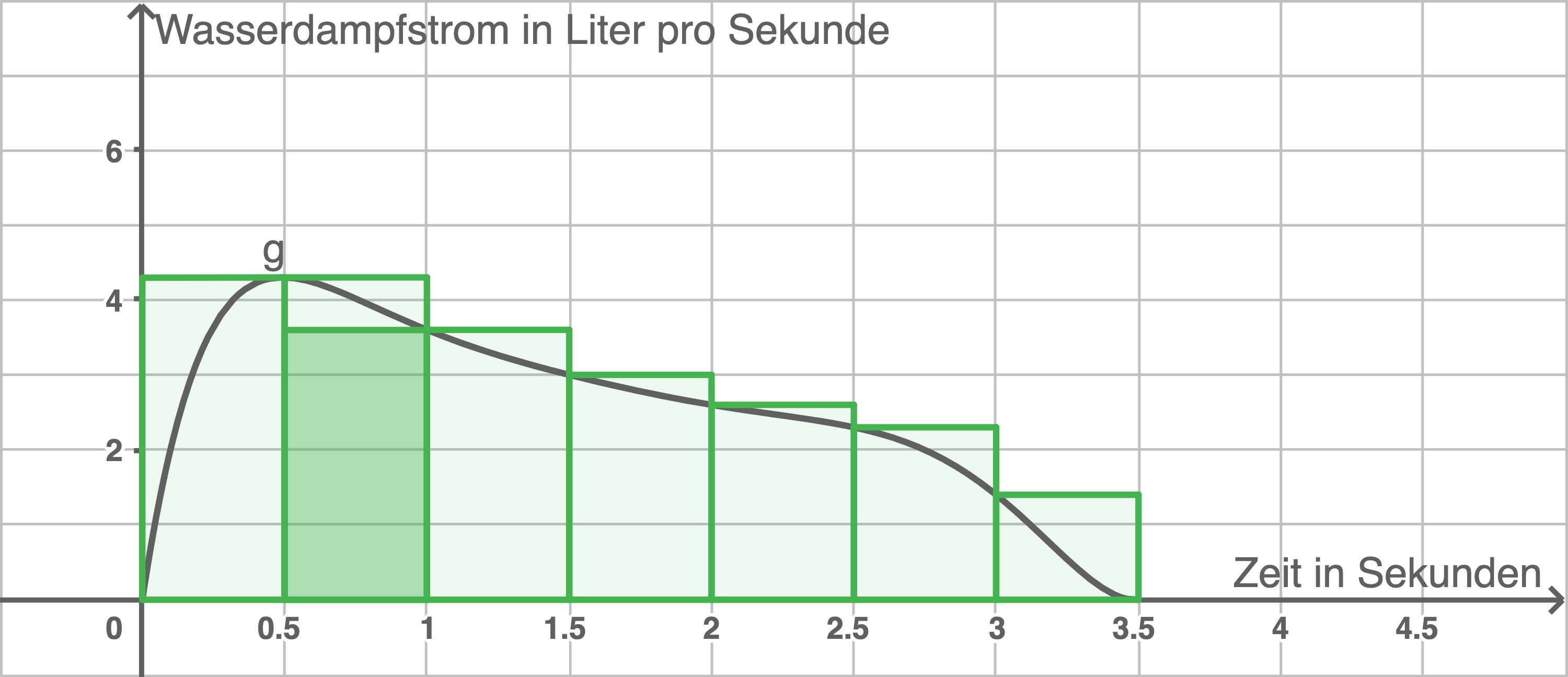

1.1
Zeichne die fehlenden Rechtecke der Untersumme  in das Koordinatensystem.
in das Koordinatensystem.
(2 BE)
1.2
Berechne die Obersumme  sowie die Untersumme
sowie die Untersumme  unter Verwendung der Wertetabelle.
unter Verwendung der Wertetabelle.
Schätze den Inhalt der Fläche ab, die der Graph der Funktion
ab, die der Graph der Funktion  mit der
mit der  -Achse im Intervall
-Achse im Intervall ![\([0;3,5]\)](https://mathjax.schullv.de/f9a140cadabb078a37e5f7103b445aa9ccd3bce63100a880c7ebdb68c1ef14a1?color=5a5a5a) einschließt.
einschließt.
Schätze den Inhalt der Fläche
(5 BE)
1.3
Erkläre unter Verwendung der Einheiten, warum der Flächeninhalt der Rechtecke aus Aufgabe 1.2 im Sachzusammenhang ein Volumen beschreibt.
(3 BE)
2.1
Der Wasserdampfstrom eines weiteren Pfeifsignals kann im Intervall ![\([0;2,6]\)](https://mathjax.schullv.de/8d5e80edb4dac4e258b642ca4630d0d53e2e6773a56cddd48b63c61b24ec99f7?color=5a5a5a) durch eine ganzrationale Funktion
durch eine ganzrationale Funktion  dritten Grades modelliert werden.
dritten Grades modelliert werden.
Hierbei soll gelten: Zu den Zeitpunkten und
und  beträgt der Wasserdampfstrom jeweils
beträgt der Wasserdampfstrom jeweils  , bei
, bei  beträgt der Wasserdampfstrom
beträgt der Wasserdampfstrom  . Zum Zeitpunkt
. Zum Zeitpunkt  besitzt die Funktion ein lokales Minimum.
besitzt die Funktion ein lokales Minimum.
Ermittle die Gleichung der Funktion . Gib hierzu die Koeffizienten auf zwei Nachkommastellen gerundet an.
. Gib hierzu die Koeffizienten auf zwei Nachkommastellen gerundet an.
Hierbei soll gelten: Zu den Zeitpunkten
Ermittle die Gleichung der Funktion
(7 BE)
Betrachtet wird im Folgenden die Funktionenschar
2.2
Für  modelliert die zugehörige Funktion den Wasserdampfstrom des Pfeifsignals aus Aufgabe 2.1. Bestimme den Zeitpunkt des maximalen Wasserdampfstroms sowie den maximalen Wasserdampfstrom.
modelliert die zugehörige Funktion den Wasserdampfstrom des Pfeifsignals aus Aufgabe 2.1. Bestimme den Zeitpunkt des maximalen Wasserdampfstroms sowie den maximalen Wasserdampfstrom.
(3 BE)
2.3
Berechne für die Modellierung mit der Funktion  das Volumen des insgesamt im Zeitraum von
das Volumen des insgesamt im Zeitraum von  bis
bis  Sekunden ausgeströmten Wasserdampfs.
Sekunden ausgeströmten Wasserdampfs.
(3 BE)
2.4
Beschreibe den Einfluss des Parameters  auf die Lage und den Wert des jeweiligen lokalen Maximums der Funktionenschar
auf die Lage und den Wert des jeweiligen lokalen Maximums der Funktionenschar  , indem man
, indem man  zwischen
zwischen  und
und  variiert. Stelle dein Ergebnis auch durch eine Skizze dar.
variiert. Stelle dein Ergebnis auch durch eine Skizze dar.
Bedründe, warum zum Beispiel zur Modellierung des Wasserdampfstroms eines Pfeifsignals nicht geeignet ist.
zur Modellierung des Wasserdampfstroms eines Pfeifsignals nicht geeignet ist.
Bedründe, warum zum Beispiel
(5 BE)
3
In der Abbildung sind Ausschnitte der Graphen der Funktionen  ,
,  und
und  dargestellt.
dargestellt.
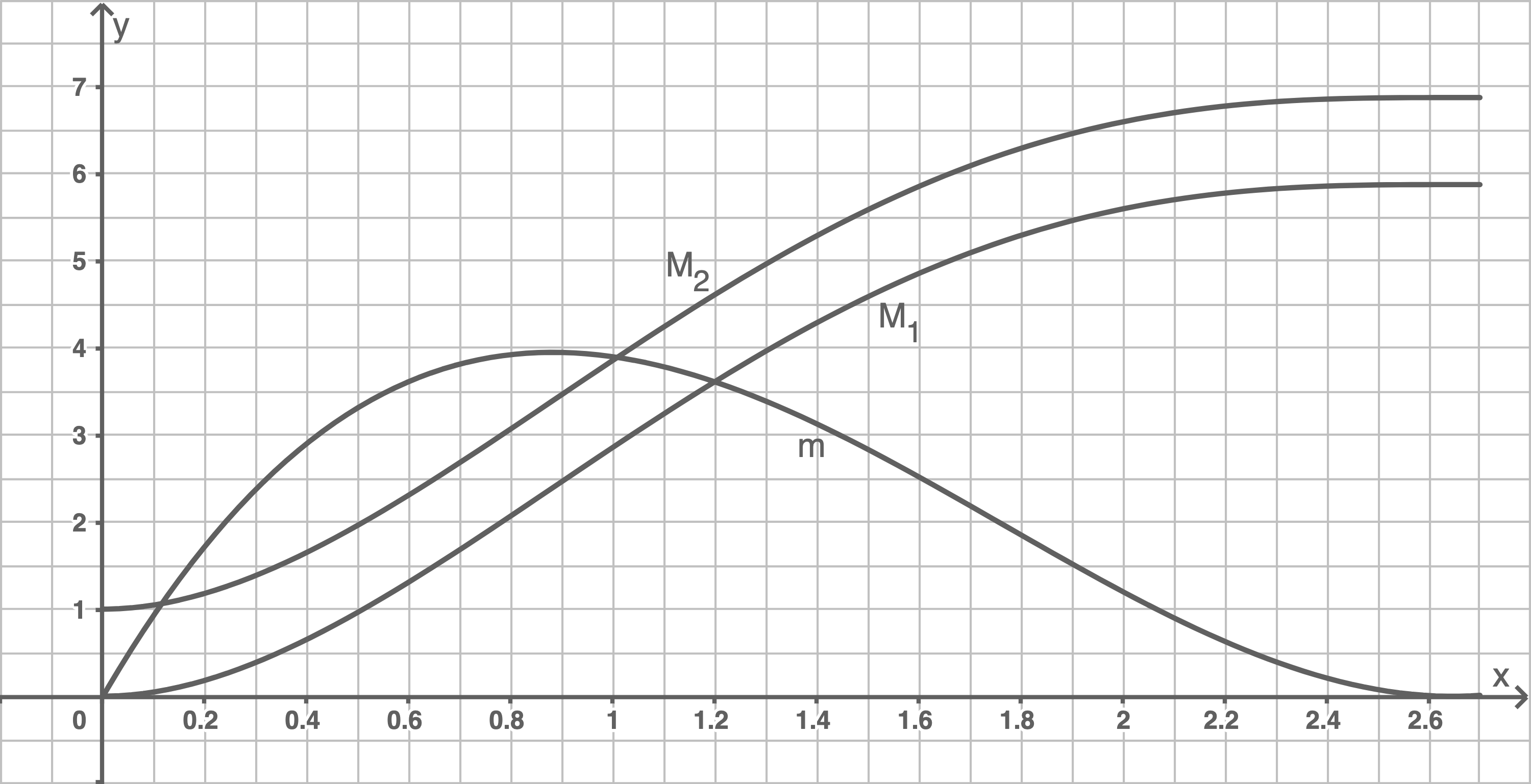

3.1
Bestätige durch Angabe von drei unterschiedlichen Argumenten, dass  und
und  mögliche Stammfunktionen von
mögliche Stammfunktionen von  sind.
sind.
(3 BE)
Der Wasserdampfstrom eines weiteren Pfeifsignals mit der Dauer von
3.2
Begründe, warum  nicht geeignet ist, das Volumen des bis zu einem beliebigen Zeitpunkt ausgeströmten Wasserdampfs dieses Pfeifsignals zu modellieren.
nicht geeignet ist, das Volumen des bis zu einem beliebigen Zeitpunkt ausgeströmten Wasserdampfs dieses Pfeifsignals zu modellieren.
Gib an und erkläre die Bedeutung dieses Werts im Sachzusammenhang.
an und erkläre die Bedeutung dieses Werts im Sachzusammenhang.
Gib
(4 BE)
3.3
Erläutere die Bedeutung der Zeilen  und
und  im Kasten.
Bestimme die Lösungen der Ungleichung in Zeile
im Kasten.
Bestimme die Lösungen der Ungleichung in Zeile  und deute diese im Sachzusammenhang.
und deute diese im Sachzusammenhang.

 Bestimme die Lösungen der Ungleichung in Zeile
Bestimme die Lösungen der Ungleichung in Zeile  und deute diese im Sachzusammenhang.
und deute diese im Sachzusammenhang.
(1)
(2)
(5 BE)
1.1
Rechtecke der Untersumme 
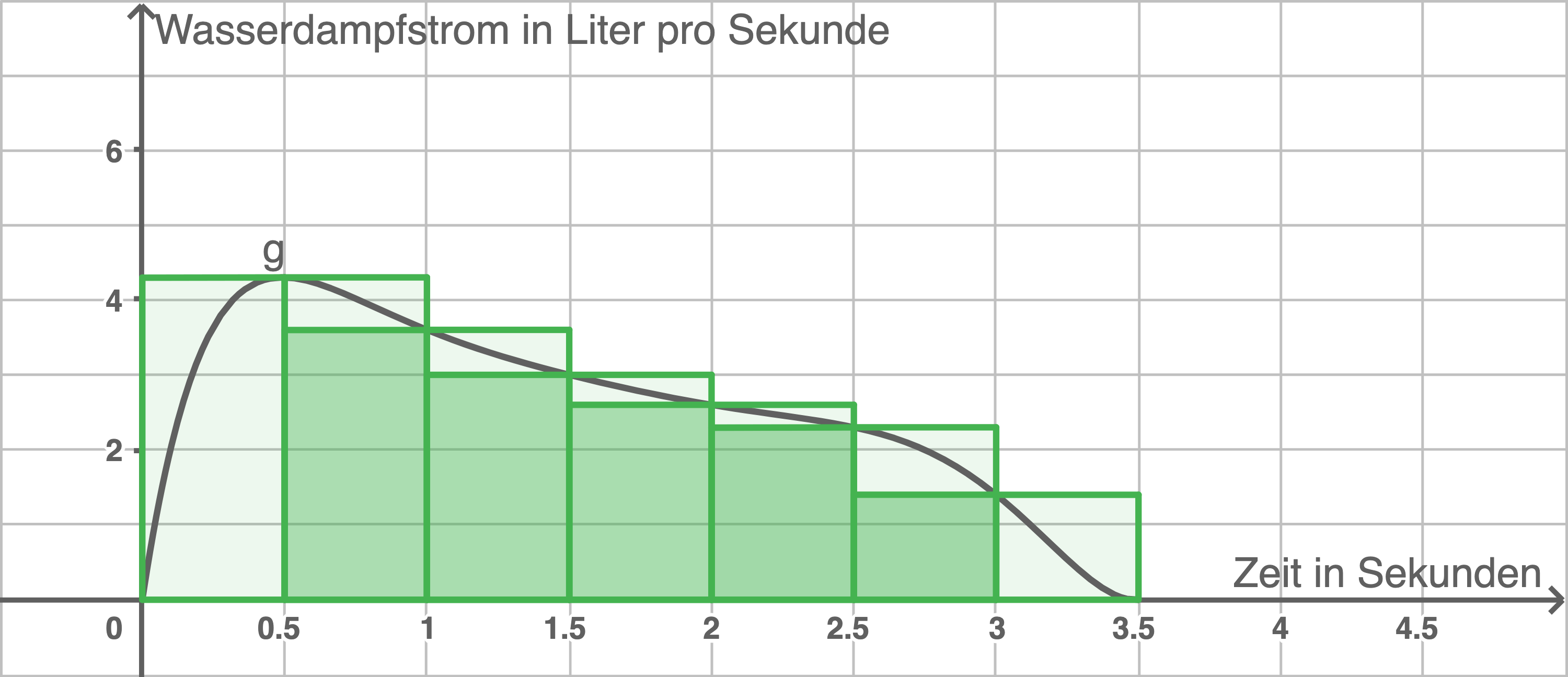

1.2
Obersumme:







 Untersumme:
Untersumme:






 Abgeschätzter Inhalt der Fläche
Abgeschätzter Inhalt der Fläche  :
:



1.3
Auf der  -Achse wird der Wasserdampfstrom in Liter pro Sekunde dargestellt:
-Achse wird der Wasserdampfstrom in Liter pro Sekunde dargestellt:  Auf der
Auf der  -Achse wird die Zeit in Sekunden erfasst:
-Achse wird die Zeit in Sekunden erfasst:  Für ein Rechteck mit der Länge
Für ein Rechteck mit der Länge  und der Breite
und der Breite  ergibt sich somit der Flächeninhalt
ergibt sich somit der Flächeninhalt  :
:
 Da es sich bei Liter um eine Volumeneinheit handelt, beschreibt der Flächeninhalt der Rechtecke im Sachzusammenhang ein Volumen.
Da es sich bei Liter um eine Volumeneinheit handelt, beschreibt der Flächeninhalt der Rechtecke im Sachzusammenhang ein Volumen.
2.1
Ganzrationale Funktion dritten Grades:
![\(\begin{array}[t]{rll}
f(x)&=& a x^3+b x^2+cx+d \quad \scriptsize \\[5pt]
f](https://mathjax.schullv.de/cabbd2547e1feadb6f5a7e2143f9659ab6ef2b3f843b09804fbe5f82f9b8d09b?color=5a5a5a) Gegebene Werte für
Gegebene Werte für  und
und  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
(1)& f(0)&=& a\cdot 0^3+b\cdot 0^2+c\cdot 0+d \quad \scriptsize \\[5pt]
&&=& 0 \\[5pt]
(2) & f(2,6)&=& a\cdot 2,6^3+b\cdot 2,6^2+c\cdot 2,6 \quad \scriptsize \\[5pt]
&&=& 0 \\[5pt]
(3) & f(0,5)&=& a\cdot 0,5^3+b\cdot 0,5^2+c\cdot 0,5 \quad \scriptsize \\[5pt]
&&=& 2,46 \\[5pt]
(4) & f](https://mathjax.schullv.de/61baf85ba385bf682ad28e3db5ee481cc70f1e347f23d8173cb32c31562deff8?color=5a5a5a) Aus der Gleichung
Aus der Gleichung  folgt, dass
folgt, dass  ist.
Die Gleichungen
ist.
Die Gleichungen  werden mithilfe des CAS Befehls für Gleichungssystem gelöst:
werden mithilfe des CAS Befehls für Gleichungssystem gelöst:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der CAS liefert die Werte
Casio Classpad II
Der CAS liefert die Werte  , für
, für  und für
und für  Für die Gleichung der Funktion
Für die Gleichung der Funktion  ergibt sich:
ergibt sich:

menu  3: Algebra
3: Algebra  7
7
keyboard  Math1
Math1 

2.2
menu  6: Graph analysieren
6: Graph analysieren  3: Maximum
3: Maximum
Analyse  Grafische Lösung
Grafische Lösung  Maximum
Maximum
2.3
Berechnen des Integrals der Funktion  mit
mit  als untere Grenze und
als untere Grenze und  als obere Grenze:
als obere Grenze:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II
![\(\displaystyle\int_{0}^{2,6}1,12\cdot t^3-k\cdot t^2+7,54\cdot t \text{ } \mathrm dt=4,3\text{[VE]}\)](https://mathjax.schullv.de/e6efd63ac46b00a36877cb25e5ac9641cc1f996a75ac0b63342476b178c4d30a?color=5a5a5a) Das Volumen des insgesamt im Zeitraum von
Das Volumen des insgesamt im Zeitraum von  bis
bis  Sekunden ausgeströmten Wasserdampfs beträgt
Sekunden ausgeströmten Wasserdampfs beträgt  .
.
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

2.4
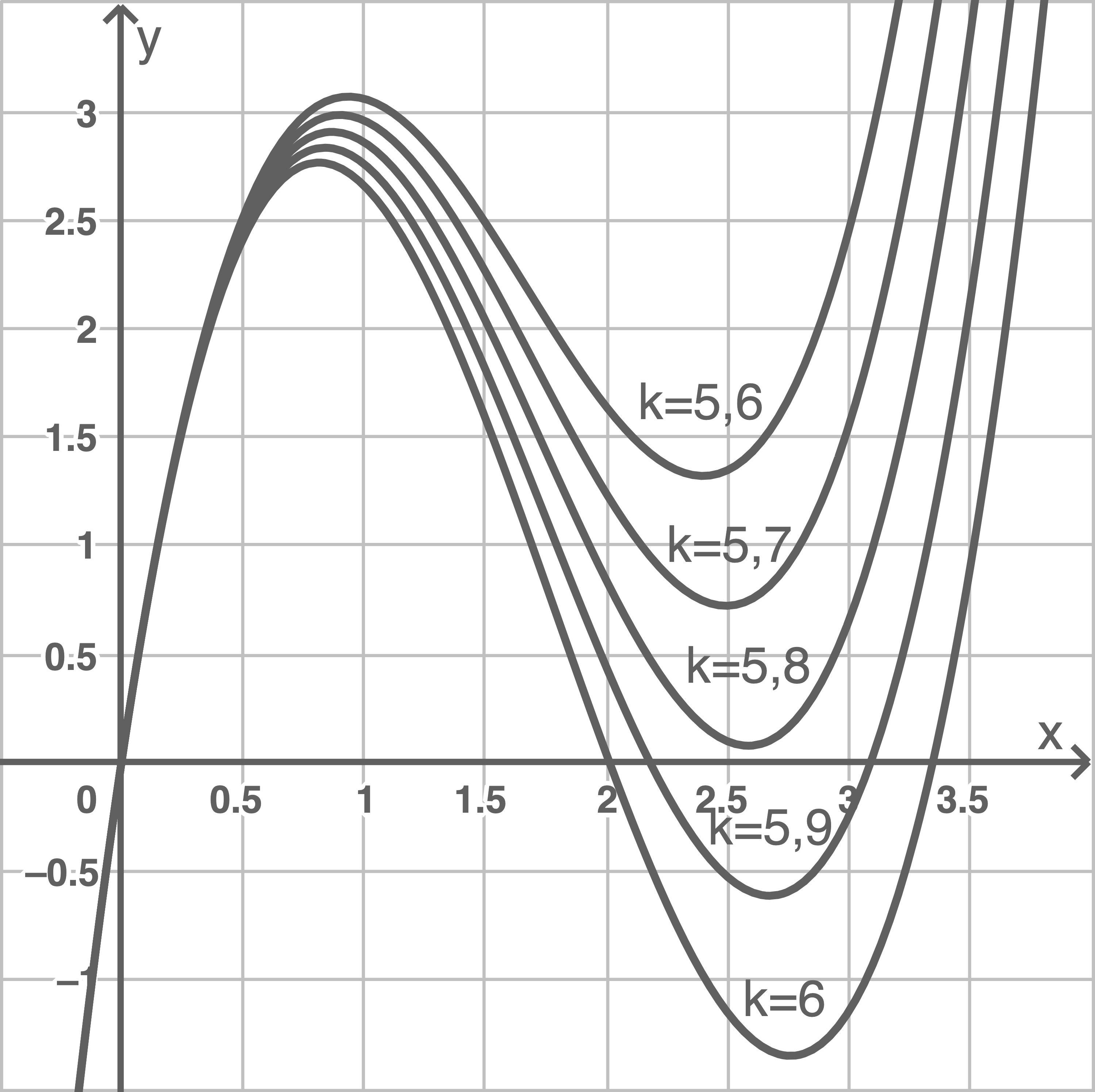
3.1
(1)
(2)
Bis etwa  ist der Graph von
ist der Graph von  monoton steigend, sodass die Graphen der Stammfunktionen in dem Intervall
monoton steigend, sodass die Graphen der Stammfunktionen in dem Intervall ![\([0;0,9]\)](https://mathjax.schullv.de/fb9760af8f98a1562d72468ea83100ca949239fac4ed2c0b7ec7c0b6f1efbfa2?color=5a5a5a) linksgekrümmt sein müssen.
linksgekrümmt sein müssen.
Ab dem Zeitpunkt ist der Graph von
ist der Graph von  monoton fallend, sodass die Graphen der Stammfunktionen ab diesem Zeitpunkt rechtsgekrümmt sein müssen.
monoton fallend, sodass die Graphen der Stammfunktionen ab diesem Zeitpunkt rechtsgekrümmt sein müssen.
Ab dem Zeitpunkt
(3)
Der Graph von  weist zum Zeitpunkt
weist zum Zeitpunkt  einen Hochpunkt auf, sodass an dieser Stelle ein Wendepunkt des Graphen der Stammfunktion existiert. Da zum Zeitpunkt
einen Hochpunkt auf, sodass an dieser Stelle ein Wendepunkt des Graphen der Stammfunktion existiert. Da zum Zeitpunkt  die Graphen
die Graphen  und
und  einen Wechsel von Linkskrümmung zu Rechtkrümmung aufweisen, handelt es sich bei
einen Wechsel von Linkskrümmung zu Rechtkrümmung aufweisen, handelt es sich bei  und
und  um mögliche Stammfunktionen von
um mögliche Stammfunktionen von  .
.
3.2
3.3
(1)
Zeile (1) ist die Ableitung der Funktion  , die das ab dem Zeitpunkt
, die das ab dem Zeitpunkt  ausgeströmte Dampfvolumen angibt. Die Ableitung
ausgeströmte Dampfvolumen angibt. Die Ableitung  gibt also den Wasserdampfstrom in Liter pro Sekunde
gibt also den Wasserdampfstrom in Liter pro Sekunde  für einen bestimmten Zeitpunkt an.
für einen bestimmten Zeitpunkt an.
(2)
Zeile (2) stellt die Frage, für welchen Zeitraum die Ableitung  größer oder gleich 3 ist bzw. - im Sachzusammenhang - für welchen Zeitraum der Wasserdampfstrom größer oder gleich
größer oder gleich 3 ist bzw. - im Sachzusammenhang - für welchen Zeitraum der Wasserdampfstrom größer oder gleich  beträgt.
beträgt.