B2 - Analysis
Eine Brauerei stellt Fassbrause (Limonade aus Malzextrakt mit Kräuterzusätzen) und alkoholfreies Bier her.
1
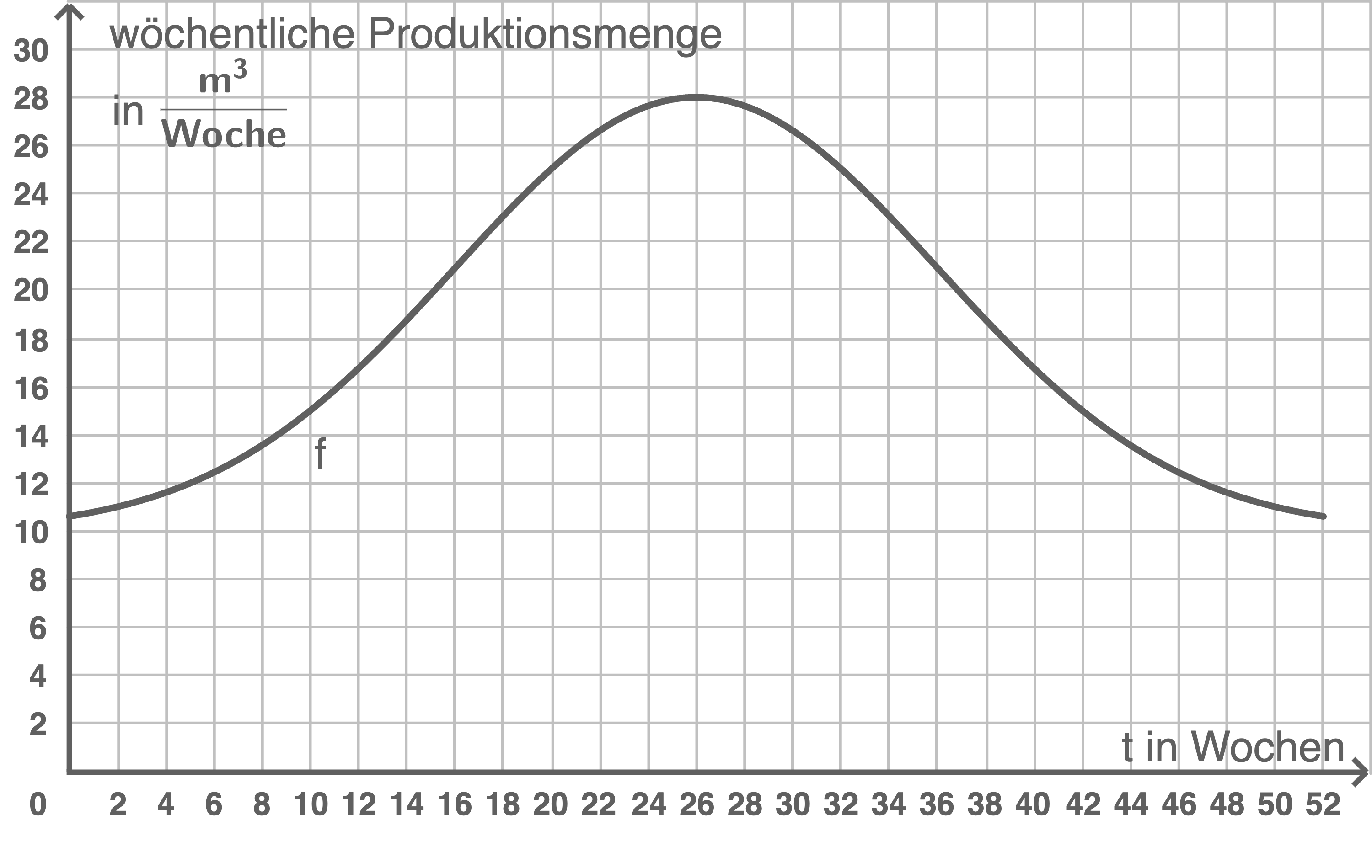
Die Entwicklung der wöchentlichen Produktionsmenge der Fassbrause über das Jahr hinweg lässt sich für das vergangene Jahr näherungsweise durch die Funktion  mit
mit
 auf dem Intervall
auf dem Intervall ![\([0;52]\)](https://mathjax.schullv.de/f4b4407257aa23d72b534a75f499cbc3cf25ac172933c73386036b18167d62b7?color=5a5a5a) modellieren. Hierbei gibt
modellieren. Hierbei gibt  die Zeit in Wochen seit Jahresbeginn an;
die Zeit in Wochen seit Jahresbeginn an;
 beschreibt die wöchentliche Produktionsmenge in
beschreibt die wöchentliche Produktionsmenge in 

1.1
Zeige rechnerisch, dass für  gilt:
gilt: 
(4 BE)
1.2
Berechne die Koordinaten des Hochpunkts des Graphen von  Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.
Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.
(4 BE)
1.3
Begründe anhand des Funktionsterms von  dass die wöchentliche Produktionsmenge den Wert von
dass die wöchentliche Produktionsmenge den Wert von  nicht überschreitet.
nicht überschreitet.
(3 BE)
1.4
Es gilt  Deute dies im Sachzusammenhang.
Deute dies im Sachzusammenhang.
(3 BE)
1.5
Es gilt:  Deute diese Berechnung im Sachzusammenhang.
Deute diese Berechnung im Sachzusammenhang.
(3 BE)
2
Für das vergangene Jahr soll die wöchentliche Produktionsmenge des alkoholfreien Biers in  zum Zeitpunkt
zum Zeitpunkt  in Wochen seit Jahresbeginn durch eine quadratische Funktion
in Wochen seit Jahresbeginn durch eine quadratische Funktion  auf dem Intervall
auf dem Intervall ![\([0;52]\)](https://mathjax.schullv.de/f4b4407257aa23d72b534a75f499cbc3cf25ac172933c73386036b18167d62b7?color=5a5a5a) beschrieben werden.
Zu Beginn des Jahres betrug die wöchentliche Produktionsmenge
beschrieben werden.
Zu Beginn des Jahres betrug die wöchentliche Produktionsmenge  Zum Zeitpunkt
Zum Zeitpunkt  Wochen wurde mit
Wochen wurde mit  die größte wöchentliche Produktionsmenge des alkoholfreien Biers erreicht.
die größte wöchentliche Produktionsmenge des alkoholfreien Biers erreicht.
2.1
Leite die Funktionsgleichung von  her und zeige, dass gilt:
her und zeige, dass gilt:
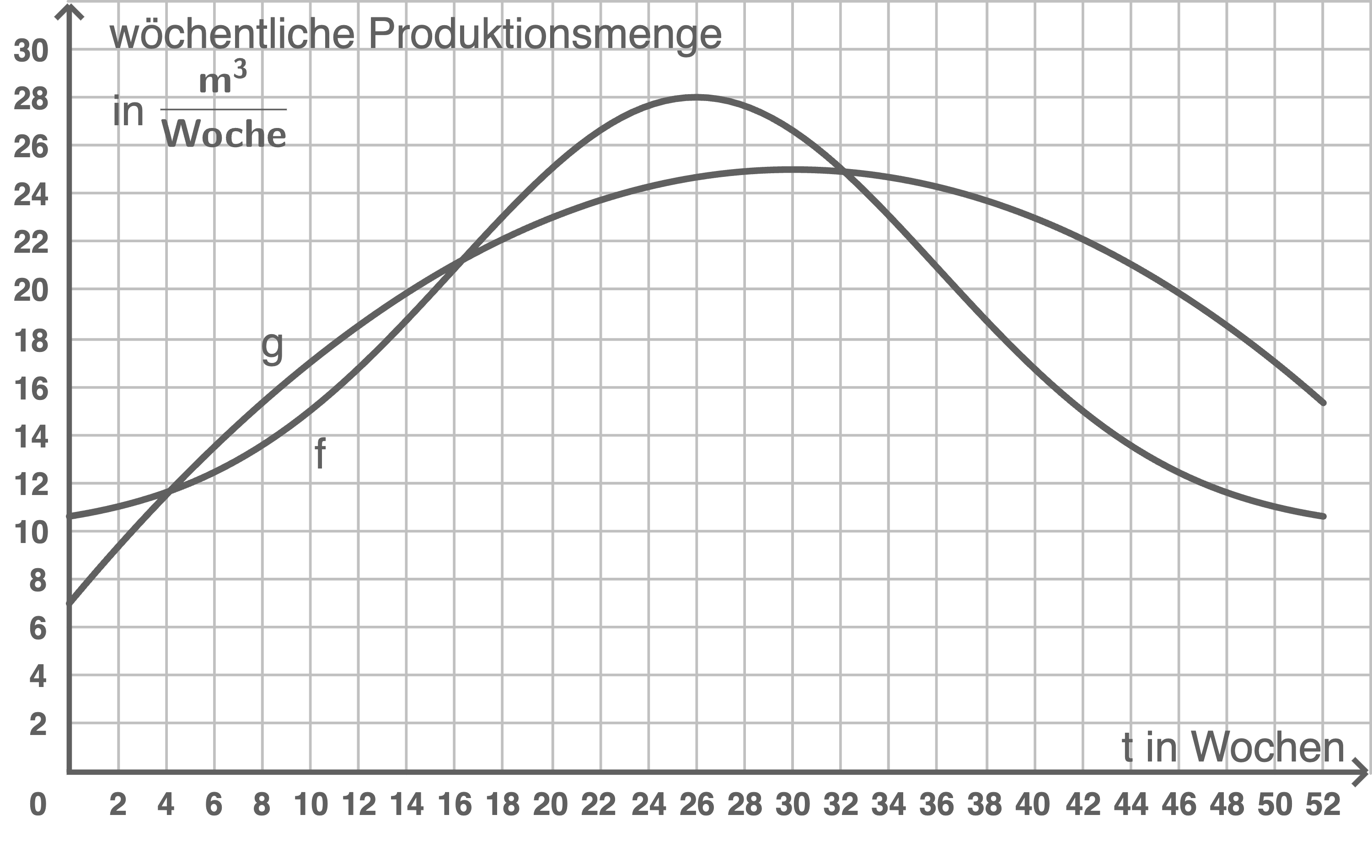
 Skizziere den Funktionsgraphen von
Skizziere den Funktionsgraphen von  in das Koordinatensystem aus der Aufgabenstellung.
in das Koordinatensystem aus der Aufgabenstellung.
(7 BE)
2.2
Der Marketingberater der Brauerei trifft die folgenden Aussagen:
- „Die Differenz zwischen der größten und der kleinsten wöchentlichen Produktionsmenge der Fassbrause und die entsprechende Differenz für das alkoholfreie Bier unterscheiden sich um weniger als
“
- „Die Gesamtproduktion der Fassbrause innerhalb des vergangenen Jahres in
war größer als die des alkoholfreien Biers.“
- „In der Nachbarbrauerei beträgt die Gesamtproduktion des alkoholfreien Biers innerhalb eines Jahres mehr als
Liter. Um dies zu erreichen, müssten wir unsere Produktion deutlich steigern.“
(8 BE)
3
Die wöchentliche Produktionsmenge des alkoholfreien Biers soll erhöht werden. Zur Modellierung dieses Sachverhalts werden im Folgenden geignete Funktionen der Funktionenschar  und
und  verwendet mit
verwendet mit  und
und  Hierbei gibt
Hierbei gibt  jeweils die Zeit in Wochen seit Jahresbeginn an;
jeweils die Zeit in Wochen seit Jahresbeginn an;  und
und  beschreiben die wöchentliche Produktionsmenge in
beschreiben die wöchentliche Produktionsmenge in  Es wird prognostiziert, dass die wöchentliche Produktionsmenge für den Zeitpunkt
Es wird prognostiziert, dass die wöchentliche Produktionsmenge für den Zeitpunkt  Wochen
Wochen  beträgt.
beträgt.
3.1
Bestimme die Parameter  und
und  der beiden Funktionenscharen so, dass zum Zeitpunkt
der beiden Funktionenscharen so, dass zum Zeitpunkt  Wochen die prognostizierte wöchentliche Produktionsmenge des alkoholfreien Biers erreicht wird.
Wochen die prognostizierte wöchentliche Produktionsmenge des alkoholfreien Biers erreicht wird.
(4 BE)
3.2
Es sei  und
und  Beschreibe jeweils im Sachzusammenhang die Wirkung des Parameters auf den Verlauf der Graphen
Beschreibe jeweils im Sachzusammenhang die Wirkung des Parameters auf den Verlauf der Graphen  bzw.
bzw.  im Vergleich zum Graphen von
im Vergleich zum Graphen von 
(4 BE)
1.1
Mit der Kettenregel ergibt sich:
1.2
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
Es gilt:
Da die Untersuchung der notwendigen Bedingung laut Aufgabenstellung ausreichend ist, folgt, dass der Graph von  seinen Hochpunkt an der Stelle
seinen Hochpunkt an der Stelle  besitzt.
2. Schritt:
besitzt.
2. Schritt:  -Koordinate berechnen
-Koordinate berechnen
![\(\begin{array}[t]{rll}
f(26)&=& 18\cdot \mathrm e^{-\frac{1}{200}(26-26)^2} + 10 \\[5pt]
&=& 28
\end{array}\)](https://mathjax.schullv.de/9e6dd61b39136525135eb5c1db3f42daa5ad01e6ba19b6a787c91a5ae174fd21?color=5a5a5a) Die Koordinaten des Hochpunkts des Graphen von
Die Koordinaten des Hochpunkts des Graphen von  lauten somit
lauten somit 
1.3
Es gilt  für alle
für alle  Der Faktor
Der Faktor  kann daher maximal den Wert
kann daher maximal den Wert  annehmen.
Insgesamt gilt daher:
annehmen.
Insgesamt gilt daher:
 Die wöchentliche Produktionsmenge kann somit den Wert von
Die wöchentliche Produktionsmenge kann somit den Wert von  nicht überschreiten.
nicht überschreiten.
1.4
Da  gilt, besitzt der Graph von
gilt, besitzt der Graph von  an der Stelle
an der Stelle  einen Wende- oder Sattelpunkt.
Aus Aufgabe 1.2 folgt, dass der einzige Extrempunkt an der Stelle
einen Wende- oder Sattelpunkt.
Aus Aufgabe 1.2 folgt, dass der einzige Extrempunkt an der Stelle  vorliegt, somit muss an der Stelle
vorliegt, somit muss an der Stelle  ein Wendepunkt, also ein Punkt mit maximaler Steigung oder maximalem Gefälle des Graphen vorliegen.
Mit der Abbildung aus der Aufgabenstellung folgt, dass der Graph von
ein Wendepunkt, also ein Punkt mit maximaler Steigung oder maximalem Gefälle des Graphen vorliegen.
Mit der Abbildung aus der Aufgabenstellung folgt, dass der Graph von  für
für  sein maximales Gefälle aufweist.
Nach 36 Wochen nimmt die wöchentliche Produktionsmenge also am stärksten ab.
sein maximales Gefälle aufweist.
Nach 36 Wochen nimmt die wöchentliche Produktionsmenge also am stärksten ab.
1.5
Mit dem Term  wird der mittlere Funktionswert von
wird der mittlere Funktionswert von  für
für  berechnet.
Dies entspricht der mittleren wöchentlichen Produktionsmenge in den ersten
berechnet.
Dies entspricht der mittleren wöchentlichen Produktionsmenge in den ersten  Wochen.
In den ersten 26 Wochen werden also im Schnitt ca.
Wochen.
In den ersten 26 Wochen werden also im Schnitt ca.  Fassbrause produziert.
Fassbrause produziert.
2.1
Funktionsgleichung von  herleiten
Allgemeine quadratische Funktionsgleichung:
herleiten
Allgemeine quadratische Funktionsgleichung:
 Hierbei sind
Hierbei sind  die Koordinaten des Hochpunkts des Graphen von
die Koordinaten des Hochpunkts des Graphen von  Die größte wöchentliche Produktionsmenge betrug laut Aufgabenstellung
Die größte wöchentliche Produktionsmenge betrug laut Aufgabenstellung  und wurde zum Zeitpunkt
und wurde zum Zeitpunkt  erreicht. Somit besitzt der Hochpunkt des Graphen von
erreicht. Somit besitzt der Hochpunkt des Graphen von  die Koordinaten
die Koordinaten  und es folgt:
und es folgt:
 Da die wöchentliche Produktionsmenge zu Beginn des Jahres
Da die wöchentliche Produktionsmenge zu Beginn des Jahres  betrug, gilt außerdem:
betrug, gilt außerdem:
![\(\begin{array}[t]{rll}
g(0) &=& 7 &\\[5pt]
a\cdot (0-30)^2 +25 &=& 7\\[5pt]
900\cdot a +25 &=& 7 &\quad \scriptsize \mid\;-25 \\[5pt]
900\cdot a &=& -18&\quad \scriptsize \mid\; :900 \\[5pt]
a &=& -0,02
\end{array}\)](https://mathjax.schullv.de/89216234e92d09f01683e4f8f4b8e54b86ce9aa6f66060d88ce78ef1caf78a33?color=5a5a5a) Eine Gleichung der Funktion
Eine Gleichung der Funktion  lautet somit
lautet somit  Anwenden der 2. binomischen Formel liefert nun:
Anwenden der 2. binomischen Formel liefert nun:
![\(\begin{array}[t]{rll}
g(t) &=& -0,02\cdot(t-30)^2+25 \\[5pt]
&=& -0,02 \cdot \left(t^2-60t +900\right)+25 \\[5pt]
&=& -0,02t^2+1,2t-18+25\\[5pt]
&=& -0,02t^2+1,2t +7
\end{array}\)](https://mathjax.schullv.de/4d76c9dfdb0be7860c4e6788fb7074520783d8deb7e23b5629f43c318d9c7f47?color=5a5a5a) Funktionsgraphen skizzieren
Funktionsgraphen skizzieren

2.2
1. Aussage
Die größte wöchentliche Produktionsmenge der Fassbrause beträgt  Da der Graph von
Da der Graph von  nur einen Extrempunkt besitzt, bei dem es sich um einen Hochpunkt handelt, kann es keinen lokalen Tiefpunkt geben. Der kleinste Funktionswert im betrachteten Intervall
nur einen Extrempunkt besitzt, bei dem es sich um einen Hochpunkt handelt, kann es keinen lokalen Tiefpunkt geben. Der kleinste Funktionswert im betrachteten Intervall ![\([0;52]\)](https://mathjax.schullv.de/f4b4407257aa23d72b534a75f499cbc3cf25ac172933c73386036b18167d62b7?color=5a5a5a) muss daher auf einem der beiden Intervallrändern liegen:
muss daher auf einem der beiden Intervallrändern liegen:
![\(\begin{array}[t]{rll}
f(0) &=& 18\cdot \mathrm e^{-\frac{1}{200}(0-26)^2}+10 \\[5pt]
&\approx& 10,613 \\[10pt]
f(52) &=& 18\cdot \mathrm e^{-\frac{1}{200}(52-26)^2}+10 \\[5pt]
&\approx& 10,613 \\[10pt]
\end{array}\)](https://mathjax.schullv.de/4a45400f8371fb569753e733dd1a5611c35e11a26757db9f5b0a5bc5f0c460aa?color=5a5a5a) Die kleinste wöchentliche Produktionsmenge der Fassbrause beträgt also ca.
Die kleinste wöchentliche Produktionsmenge der Fassbrause beträgt also ca.  Die Differenz zwischen der kleinsten und der größten wöchentlichen Produktionsmenge der Fassbrause beträgt folglich ca.
Die Differenz zwischen der kleinsten und der größten wöchentlichen Produktionsmenge der Fassbrause beträgt folglich ca.  Die größte wöchentliche Produktionsmenge des alkoholfreien Biers beträgt
Die größte wöchentliche Produktionsmenge des alkoholfreien Biers beträgt  Da die Funktion
Da die Funktion  quadratisch ist, kann auch ihr Graph keinen weiteren Extrempunkt als den Hochpunkt besitzen. Hier muss also ebenfalls der kleinste Funktionswert auf einem der beiden Intervallränder angenommen werden:
quadratisch ist, kann auch ihr Graph keinen weiteren Extrempunkt als den Hochpunkt besitzen. Hier muss also ebenfalls der kleinste Funktionswert auf einem der beiden Intervallränder angenommen werden:
![\(\begin{array}[t]{rll}
g(0) &=& -0,02\cdot 0^2 +1,2\cdot 0 +7 \\[5pt]
&=& 7 \\[10pt]
g(52) &=& -0,02\cdot 52^2 +1,2\cdot 52 +7 \\[5pt]
&=& 15,32 \\[10pt]
\end{array}\)](https://mathjax.schullv.de/2c4dc1e4612b589ed593064ca7858b97024d1820959d541d311ac5936af25749?color=5a5a5a) Die kleinste wöchentliche Produktionsmenge des alkoholfreien Biers beträgt also
Die kleinste wöchentliche Produktionsmenge des alkoholfreien Biers beträgt also  Die Differenz zwischen der kleinsten und der größten wöchentlichen Produktionsmenge des alkoholfreien Biers beträgt also ca.
Die Differenz zwischen der kleinsten und der größten wöchentlichen Produktionsmenge des alkoholfreien Biers beträgt also ca.  Die Differenz zwischen der größten und der kleinsten wöchentlichen Produktionsmenge der Fassbrause und die entsprechende Differenz des alkoholfreien Biers unterscheiden sich also um ca.
Die Differenz zwischen der größten und der kleinsten wöchentlichen Produktionsmenge der Fassbrause und die entsprechende Differenz des alkoholfreien Biers unterscheiden sich also um ca.  Diese Aussage des Beraters ist also wahr.
2. Aussage
Aus Aufgabe 1.5 folgt:
Diese Aussage des Beraters ist also wahr.
2. Aussage
Aus Aufgabe 1.5 folgt:
![\(\begin{array}[t]{rll}
\dfrac{1}{26}\displaystyle\int_{0}^{26}f(t)\;\mathrm dt &\approx& 18,6 &\quad \scriptsize \mid\; \cdot 26 \\[5pt]
\displaystyle\int_{0}^{26}f(t)\;\mathrm dt &=& 483,6
\end{array}\)](https://mathjax.schullv.de/fec06433c2e5e7afe81000a50e275e56fee485356bb28197cc57ab17f25e334b?color=5a5a5a) Aufgrund der Symmetrie des Graphen von
Aufgrund der Symmetrie des Graphen von  ergibt sich die Gesamtproduktion der Fassbrause zu:
ergibt sich die Gesamtproduktion der Fassbrause zu:
![\(\begin{array}[t]{rll}
\displaystyle\int_{0}^{52}f(t)\;\mathrm dt&=& 2\cdot \displaystyle\int_{0}^{26}f(t)\;\mathrm dt \\[5pt]
&\approx & 2\cdot 483,6 \\[5pt]
&=& 967,2 \;[\text{m}^3]\\[5pt]
\end{array}\)](https://mathjax.schullv.de/c5722d43c2b1d31c9ce1b20f44eaf86f13bc2abdd86cfce97e657baebb7948c2?color=5a5a5a) Für die Gesamtproduktion des alkoholfreien Biers gilt:
Alternativ können die beiden Integrale auch mit dem CAS berechnet werden:
Für die Gesamtproduktion des alkoholfreien Biers gilt:
Alternativ können die beiden Integrale auch mit dem CAS berechnet werden:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Damit war die Gesamtproduktion des alkoholfreien Biers im vergangenen Jahr größer als die der Fassbrause.
Die zweite Aussage des Beraters ist somit nicht korrekt.
3. Aussage
Im vergangenen Jahr hat die betrachtete Brauerei ca.
Casio Classpad II
Damit war die Gesamtproduktion des alkoholfreien Biers im vergangenen Jahr größer als die der Fassbrause.
Die zweite Aussage des Beraters ist somit nicht korrekt.
3. Aussage
Im vergangenen Jahr hat die betrachtete Brauerei ca.  alkoholfreies Bier produziert.
Es gilt
alkoholfreies Bier produziert.
Es gilt  und somit
und somit  Dies sind mehr als die Gesamtproduktion der Nachbarbrauerei von
Dies sind mehr als die Gesamtproduktion der Nachbarbrauerei von  Die dritte Aussage des Beraters ist also ebenfalls falsch.
Die dritte Aussage des Beraters ist also ebenfalls falsch.
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

3.1
Für  soll gelten:
Analog ergibt sich für
soll gelten:
Analog ergibt sich für  Für
Für  und
und  wird zum Zeitpunkt
wird zum Zeitpunkt  die prognostizierte wöchentliche Produktionsmenge des alkoholfreien Biers erreicht.
die prognostizierte wöchentliche Produktionsmenge des alkoholfreien Biers erreicht.
3.2
Der Parameter  führt zu einer Streckung des Graphen von
führt zu einer Streckung des Graphen von  in
in  -Richtung. Dadurch wird die wöchentliche Produktionsmenge zu jedem Zeitpunkt um das 1,4-Fache erhöht.
Der Parameter
-Richtung. Dadurch wird die wöchentliche Produktionsmenge zu jedem Zeitpunkt um das 1,4-Fache erhöht.
Der Parameter  verschiebt den Graphen von
verschiebt den Graphen von  in positive
in positive  -Richtung. Dadurch wird die wöchentliche Produktionsmenge zu jedem Zeitpunkt um
-Richtung. Dadurch wird die wöchentliche Produktionsmenge zu jedem Zeitpunkt um  erhöht.
erhöht.
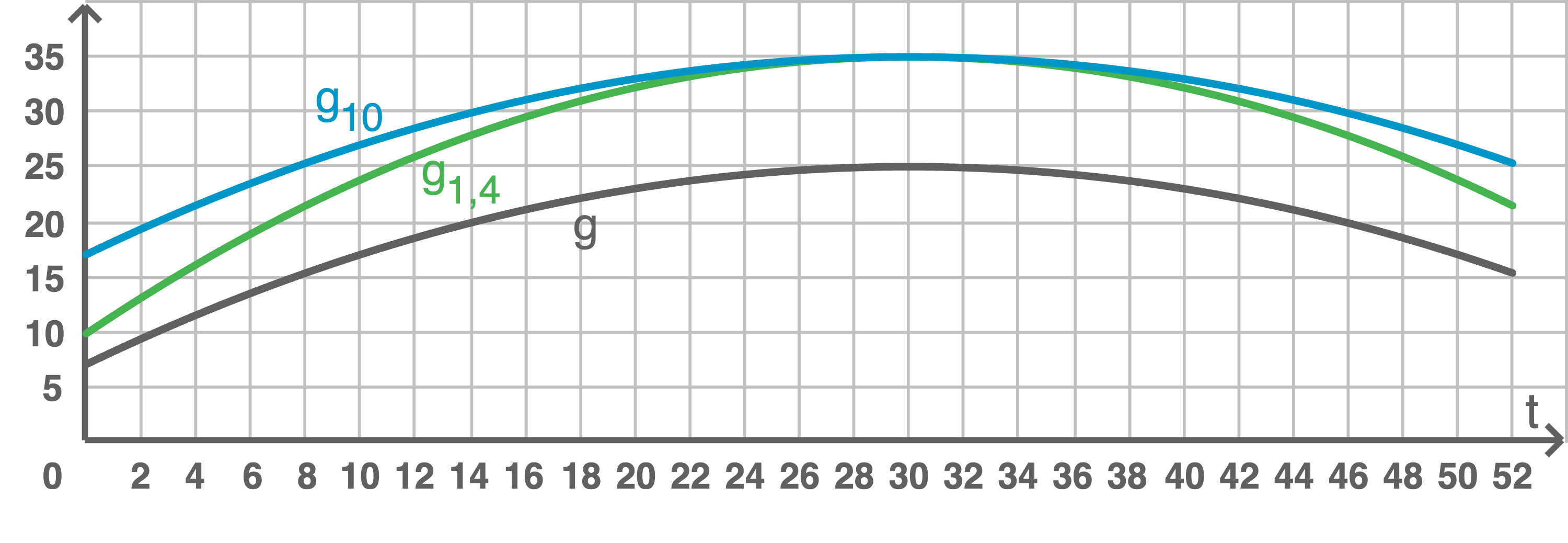

Hilfsskizze