B2 - Analysis
Der Ederstausee in Hessen ist bezogen auf sein Volumen der drittgrößte Stausee in Deutschland und wird unter anderem dazu genutzt, die Schifffahrt auf der Weser in den Sommermonaten sicherzustellen.
Sein maximales Fassungsvermögen beträgt rund 200 Millionen Kubikmeter Wasser. Über eine Staumauer wird der Pegelstand und somit die Füllmenge reguliert.
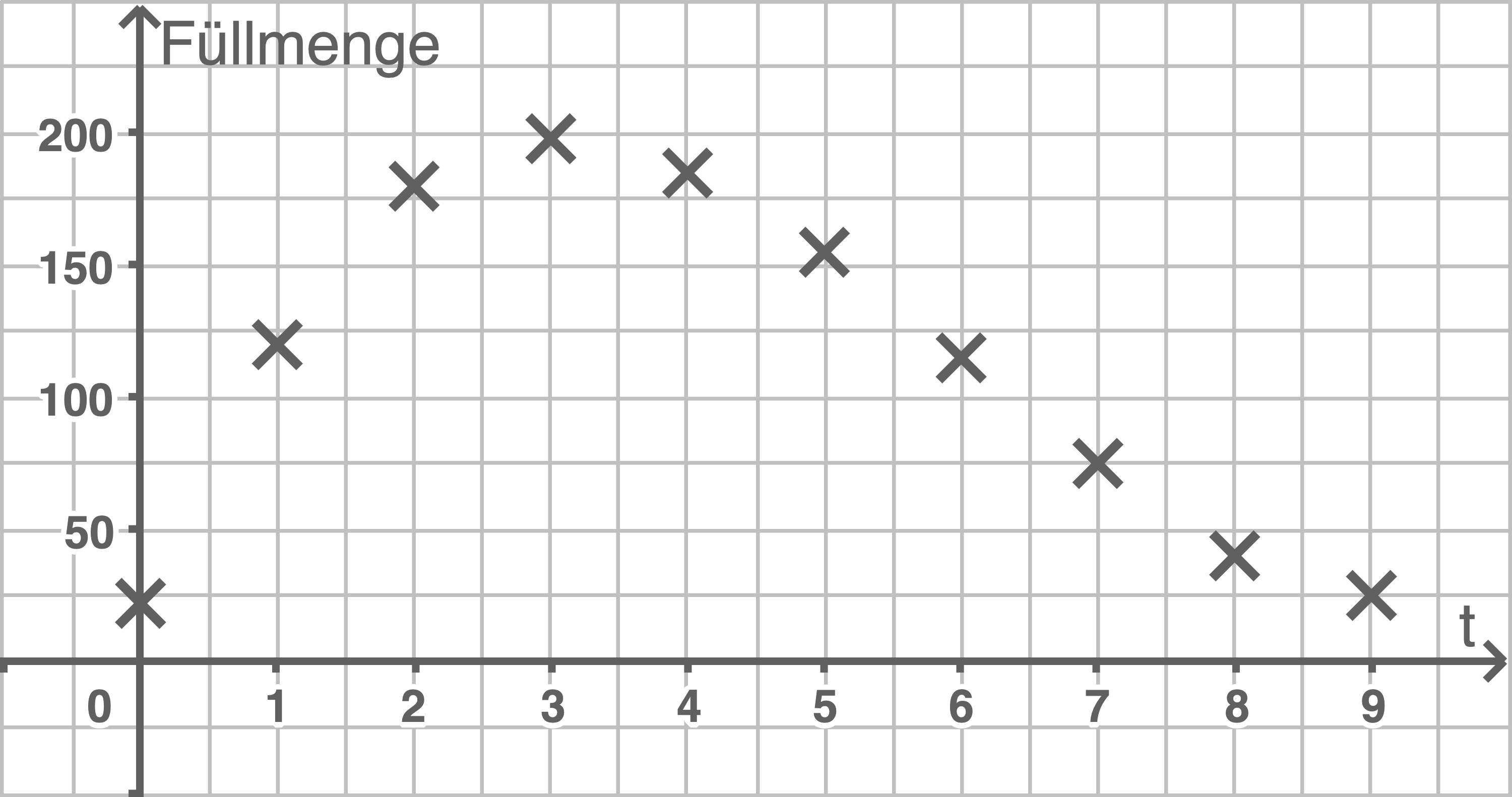
Für die Monate Januar  bis Oktober 2019 konnten folgende Füllmengen ermittelt werden:
bis Oktober 2019 konnten folgende Füllmengen ermittelt werden:
Dabei beziehen sich die Zeitpunkte  jeweils auf die Monatsmitte, die Füllmengen sind Mittelwerte der jeweiligen Monate. Vereinfachend wird angenommen, dass jeder Monat mit 30 Tagen gleich lang ist.
jeweils auf die Monatsmitte, die Füllmengen sind Mittelwerte der jeweiligen Monate. Vereinfachend wird angenommen, dass jeder Monat mit 30 Tagen gleich lang ist.
| Zeit |
Füllmenge in |
|---|---|
1
Die Füllmenge des Stausees  in
in  soll in Abhängigkeit von der Zeit
soll in Abhängigkeit von der Zeit  (in Monaten) näherungsweise durch verschiedene Funktionen modelliert werden.
(in Monaten) näherungsweise durch verschiedene Funktionen modelliert werden.
1.1
Zeichne die gegebenen Datenpunkte in ein skaliertes und beschriftetes Koordinatensystem ein.
(3 BE)
1.2
Die Füllmenge des Stausees soll durch zwei ganzrationale Funktionen dritten Grades,  und
und  modelliert werden.
modelliert werden.
1.2.1
Bestimme die Funktionsgleichung der Funktion  deren Graph durch die vier Datenpunkte zu den Zeitpunkten
deren Graph durch die vier Datenpunkte zu den Zeitpunkten  und
und  verläuft.
verläuft.
(4 BE)
1.2.2
Erläutere den folgenden Lösungsansatz zur Rekonstruktion der Funktion  Beurteile, ob er geeignet ist.
Beurteile, ob er geeignet ist.
![\(\begin{array}[t]{rll}
(1)&& g(1)&=&120 \\[5pt]
(2)&& g(6)&=&115 \\[5pt]
(3)&& g](https://mathjax.schullv.de/adf24dc7fa4183f5cc4e472069d5ae520c415049f6260a74b91e46961a7798d7?color=5a5a5a)
(4 BE)
1.3
Eine andere Näherungsfunktion für die Modellierung der Füllmenge des Stausees ist die Funktion  mit
mit  Bestimme mithilfe der Funktionsgleichung unter Angabe aller notwendigen Ableitungen die Extrem- und Wendepunkte des Graphen von
Bestimme mithilfe der Funktionsgleichung unter Angabe aller notwendigen Ableitungen die Extrem- und Wendepunkte des Graphen von  und deute die Ergebnisse im Sachzusammenhang.
und deute die Ergebnisse im Sachzusammenhang.
(8 BE)
1.4
Berechne die mittlere Füllmenge des Stausees in den Monaten April bis Oktober, die sich aus den Datenpunkten der zu Beginn der Aufgabe gegebenen Tabelle ergibt.
Entscheide begründet ohne weitere Rechnung, mit welchem der nachfolgenden Terme die mittlere Füllmenge des Stausees in dem betrachteten Zeitraum näherungsweise berechnet werden kann und mit welchem nicht.



(5 BE)
2
Am Fuße der Staumauer befindet sich das Kraftwerk Hemfurth I, welches aus dem herabströmenden Wasser Strom erzeugt.
Die Zuflussgeschwindigkeit durch den Fluss "Eder" in den Stausee beträgt konstant  Durch den zusätzlichen Zulauf durch Bäche ist die tatsächliche Zuflussgeschwindigkeit allerdings um
Durch den zusätzlichen Zulauf durch Bäche ist die tatsächliche Zuflussgeschwindigkeit allerdings um  höher.
Für die Stromerzeugung wird täglich in der Zeit von
höher.
Für die Stromerzeugung wird täglich in der Zeit von  Uhr bis
Uhr bis  Uhr Wasser abgegeben. Die Abflussgeschwindigkeit aus dem Stausee beträgt hierbei konstant
Uhr Wasser abgegeben. Die Abflussgeschwindigkeit aus dem Stausee beträgt hierbei konstant  Untersuche anhand einer geeigneten Rechnung die Auswirkung der Zu- und Abflüsse auf die tägliche Füllmenge des Stausees.
Untersuche anhand einer geeigneten Rechnung die Auswirkung der Zu- und Abflüsse auf die tägliche Füllmenge des Stausees.
(4 BE)
3
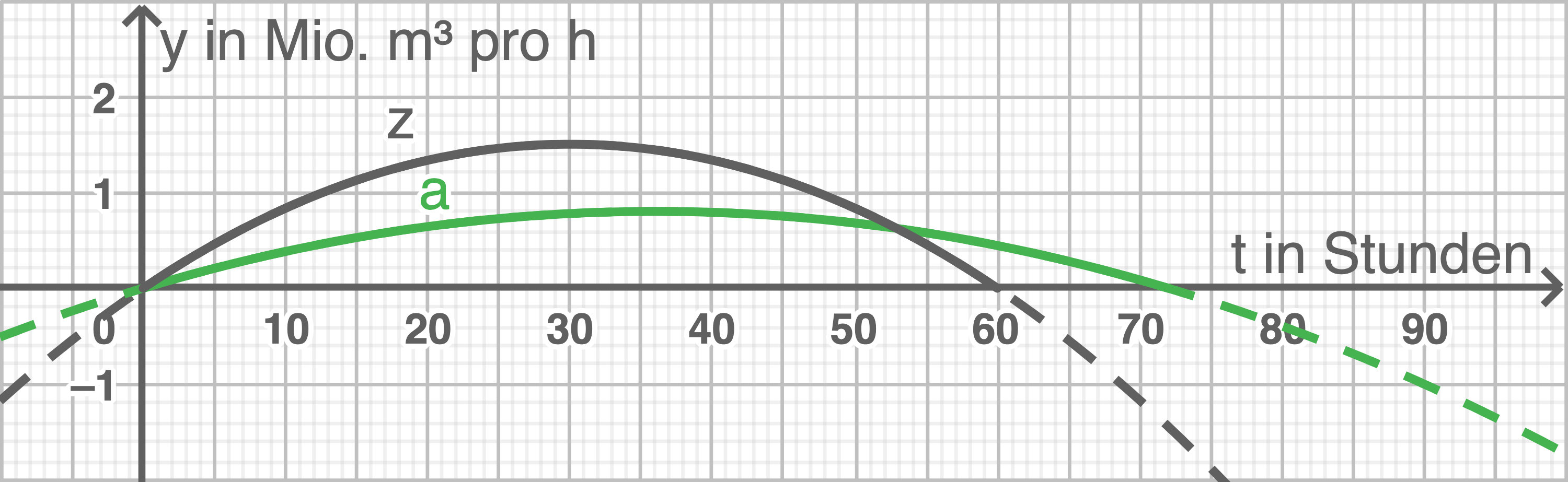
Zum Schutz vor Hochwasser wird im Stausee ein sogenannter Hochwasserschutzraum mit einem Volumen von  freigehalten. Nach starken Regenfällen kann die Zuflussgeschwindigkeit des Wassers in den Stausee innerhalb der ersten 72 Stunden durch die Funktion
freigehalten. Nach starken Regenfällen kann die Zuflussgeschwindigkeit des Wassers in den Stausee innerhalb der ersten 72 Stunden durch die Funktion  mit
mit  und die Abflussgeschwindigkeit nach dem Öffnen von Notschleusen durch die Funktion
und die Abflussgeschwindigkeit nach dem Öffnen von Notschleusen durch die Funktion  mit
mit  dargestellt werden.
Hierbei gibt
dargestellt werden.
Hierbei gibt  jeweils die Zeit in Stunden ab dem Beginn des Zu- bzw. Abflusses an und
jeweils die Zeit in Stunden ab dem Beginn des Zu- bzw. Abflusses an und  bzw.
bzw.  die Fließgeschwindigkeit in
die Fließgeschwindigkeit in  Dabei sind die Funktionen
Dabei sind die Funktionen  und
und  nur in Intervallen mit positiven Funktionswerten definiert, sonst seien die Funktionswerte konstant null.
nur in Intervallen mit positiven Funktionswerten definiert, sonst seien die Funktionswerte konstant null.

3.1
Erläutere die folgende Rechnung im Sachzusammenhang.
Begründe, dass die getroffene Schlussfolgerung nicht richtig sein muss.


Der Hochwasserschutzraum von ist ausreichend, da in dem betrachteten Zeitraum nur
ist ausreichend, da in dem betrachteten Zeitraum nur  mehr zu- als abfließen.
mehr zu- als abfließen.
Der Hochwasserschutzraum von
(3 BE)
3.2
Ermittle den Zeitpunkt, zu dem die Füllmenge des Hochwasserschutzraums in den betrachteten 72 Stunden maximal ist.
(3 BE)
4
Die maximale Füllhöhe  über dem tiefsten Punkt des Sees beträgt ca.
über dem tiefsten Punkt des Sees beträgt ca.  die maximale Füllhöhe
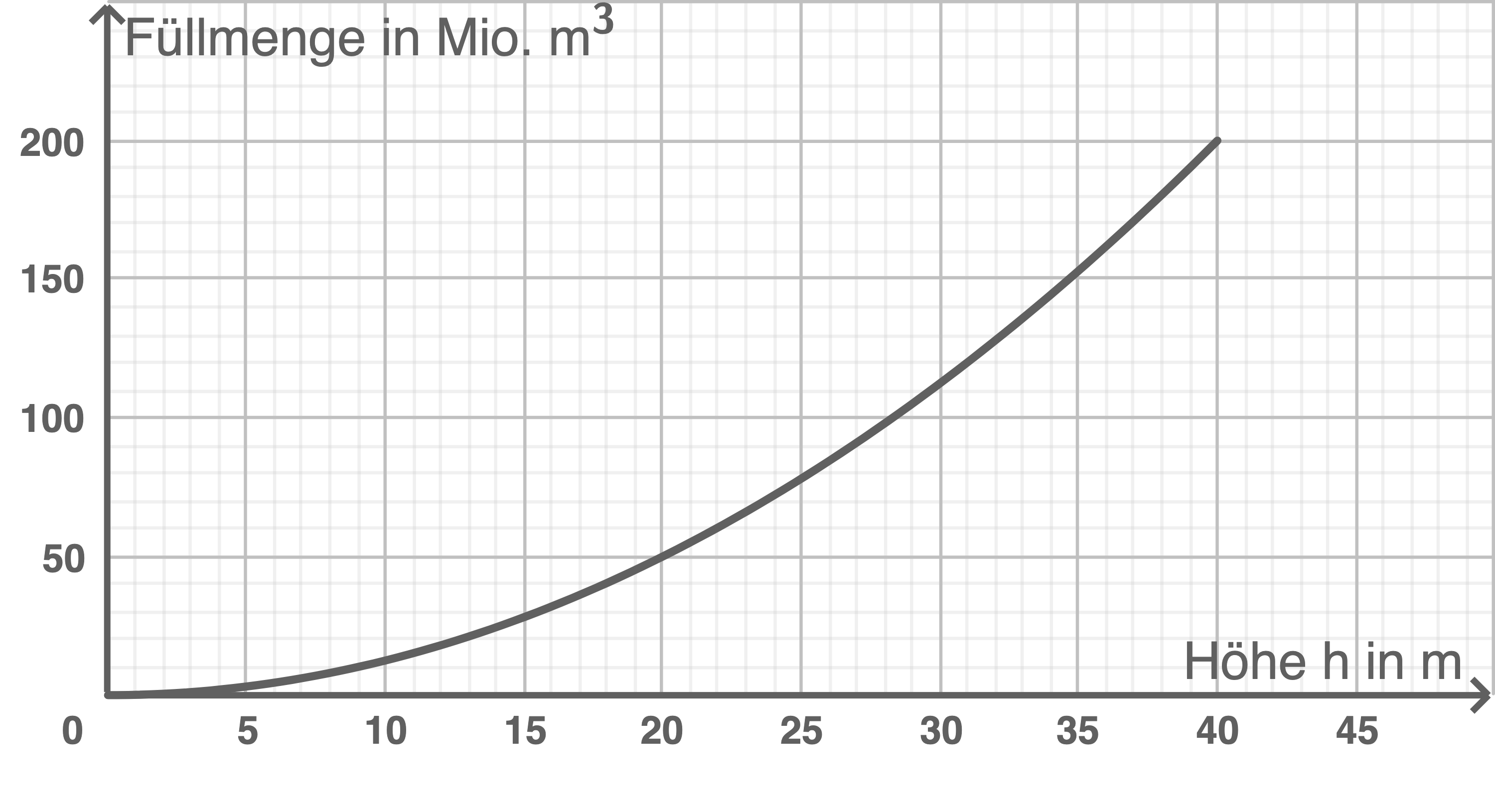
die maximale Füllhöhe  Der zugehörige Füllgraph, der die Füllmenge
Der zugehörige Füllgraph, der die Füllmenge  des Sees in
des Sees in  in Abhängigkeit von der Höhe
in Abhängigkeit von der Höhe  der Wasseroberfläche über dem tiefsten Punkt des Sees in Meter beschreibt, ist in der folgenden Abbildung dargestellt und kann durch eine quadratische Funktion
der Wasseroberfläche über dem tiefsten Punkt des Sees in Meter beschreibt, ist in der folgenden Abbildung dargestellt und kann durch eine quadratische Funktion  beschrieben werden.
beschrieben werden.

4.1
Im Folgenden sind zwei stark vereinfachte Formen eines Seebeckens vorgegeben.
Entscheide, welche der Formen zum Füllgraph  gehört, und welche nicht. Begründe jeweils deine Entscheidung unter Bezugnahme auf die beiden Formen.
gehört, und welche nicht. Begründe jeweils deine Entscheidung unter Bezugnahme auf die beiden Formen.
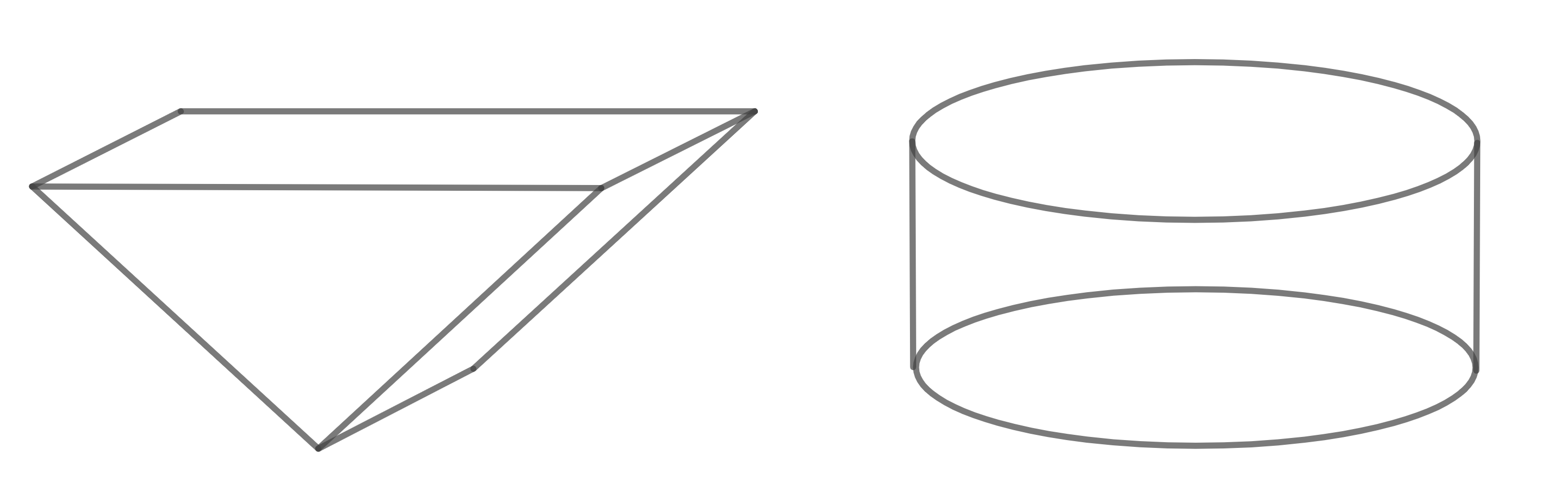

Abb.: Prisma (links), Zylinder (rechts)
(4 BE)
4.2
Durch das Fluten des Edersees befinden sich heute einige Gebäude, Straßen und Brücken je nach Füllmenge des Sees unter Wasser. Beträgt die Füllmenge des Sees nur ca.  kommt der alte Friedhof wieder zum Vorschein.
Ermittle mithilfe der Abbildung aus der Aufgabenstellung die zugehörige Höhe
kommt der alte Friedhof wieder zum Vorschein.
Ermittle mithilfe der Abbildung aus der Aufgabenstellung die zugehörige Höhe  der Wasseroberfläche über dem tiefsten Punkt des Sees.
der Wasseroberfläche über dem tiefsten Punkt des Sees.
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
1.1
1.2
1.2.1
Eine ganzrationale Funktion dritten Grades lautet:
 Es gilt:
Es gilt:
![\(\text{I}: \begin{array}[t]{rll}
f(0)&=& 22 &\\[5pt]
a\cdot 0^3+b\cdot 0^2+c\cdot 0+d &=& 22 &\\[5pt]
d&=& 22
\end{array}\)](https://mathjax.schullv.de/f1367333f7a3066465c8a10f040f7e5d0945d8a72cdf634cd15a7ca7df3be24f?color=5a5a5a) Mit dem CAS können die Gleichungen
Mit dem CAS können die Gleichungen  und
und  nach den Parametern
nach den Parametern  aufgelöst werden.
aufgelöst werden.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Es ergeben sich:
Casio Classpad II
Es ergeben sich:

 Daraus folgt:
Daraus folgt:

menu  3: Algebra
3: Algebra  7
7
keyboard  Math1
Math1 

1.2.2
Durch die drei gegebenen Bedingungen wird die Funktion so rekonstruiert, dass sie die Daten des ersten und sechsten Monates beinhaltet. Die dritte Bedingung legt den sechsten Monat als Wendestelle fest.
Dies entspricht zwar dem Verlauf der Füllmenge des Stausees, jedoch werden mindestens vier Gleichungen benötigt, um eine ganzrationale Funktion dritten Grades mit den Parametern  und
und  aufstellen zu können. Das Gleichungssystem ist somit unterbestimmt.
Mit dem angegebenen Lösungsansatz können die Parameter folglich nur in Abhängigkeit eines anderen Parameters bestimmt werden. Der Lösungsansatz ist deshalb eher ungeeignet.
aufstellen zu können. Das Gleichungssystem ist somit unterbestimmt.
Mit dem angegebenen Lösungsansatz können die Parameter folglich nur in Abhängigkeit eines anderen Parameters bestimmt werden. Der Lösungsansatz ist deshalb eher ungeeignet.
1.3
1. Schritt: Ableitungen bestimmen
 Mit dem CAS werden die ersten beiden Ableitungen ermittelt:
Mit dem CAS werden die ersten beiden Ableitungen ermittelt:

 2. Schritt: Extrempunkte bestimmen
Mit dem CAS lassen sich die Koordinaten der Extrem- und Wendepunkte graphisch ablesen:
2. Schritt: Extrempunkte bestimmen
Mit dem CAS lassen sich die Koordinaten der Extrem- und Wendepunkte graphisch ablesen:


 Sachzusammenhang deuten
Im April ist die Füllmenge des Stausees maximal mit einem Volumen von etwa
Sachzusammenhang deuten
Im April ist die Füllmenge des Stausees maximal mit einem Volumen von etwa  Millionen
Millionen  und im Oktober ist die Füllmenge minimal mit einem Volumen von etwa
und im Oktober ist die Füllmenge minimal mit einem Volumen von etwa  Millionen
Millionen  . Im Juli nimmt die Füllmenge am stärksten ab.
. Im Juli nimmt die Füllmenge am stärksten ab.
1.4
Mittlere Füllmenge berechnen
Terme deuten
Term (2) berechnet näherungsweise die mittlere Füllmenge des Stausees im betrachteten Zeitraum. Der Zeitpunkt  bezieht sich auf auf die Monatsmitte, weshalb die Integrationsgrenzen dem Monatsanfang und dem Ende des Monats entsprechen.
Term (1) beschreibt die mittlere Füllmenge nur im Zeitraum von Mitte April bis Mitte Oktober, also nur für sechs Monate, und ist somit nicht korrekt.
bezieht sich auf auf die Monatsmitte, weshalb die Integrationsgrenzen dem Monatsanfang und dem Ende des Monats entsprechen.
Term (1) beschreibt die mittlere Füllmenge nur im Zeitraum von Mitte April bis Mitte Oktober, also nur für sechs Monate, und ist somit nicht korrekt.
2
Zufluss bis 17 Uhr
Zwischen 0 Uhr und 17 Uhr beträgt die Zuflussgeschwindigkeit konstant  Da diese durch den Zufluss der Bäche um
Da diese durch den Zufluss der Bäche um  erhöht wird, folgt für die gesamte Zuflussgeschwindigkeit:
erhöht wird, folgt für die gesamte Zuflussgeschwindigkeit:
 In den ersten 17 Stunden lässt sich der gesamte Zulauf somit wie folgt berechnen:
In den ersten 17 Stunden lässt sich der gesamte Zulauf somit wie folgt berechnen:
 Zu- und Abfluss von 17 Uhr bis 21.15 Uhr
Der Zeitraum, in welchem Wasser abfließt, entspricht 255 Minuten und somit
Zu- und Abfluss von 17 Uhr bis 21.15 Uhr
Der Zeitraum, in welchem Wasser abfließt, entspricht 255 Minuten und somit  Sekunden.
Für den Abfluss gilt somit:
Sekunden.
Für den Abfluss gilt somit:
 Gleichzeitig gilt für den Zufluss in diesem Zeitraum:
Gleichzeitig gilt für den Zufluss in diesem Zeitraum:
 Von 0 Uhr bis 21.15 Uhr sind somit insgesamt
Von 0 Uhr bis 21.15 Uhr sind somit insgesamt  zugeflossen und
zugeflossen und  abgeflossen. Im Vergleich zur Füllmenge des Stausees zu Tagesbeginn sind zu diesem Zeitpunkt
abgeflossen. Im Vergleich zur Füllmenge des Stausees zu Tagesbeginn sind zu diesem Zeitpunkt  Wasser weniger im See.
Zufluss bis 0 Uhr
Der Zeitraum von 21.15 Uhr bis 0 Uhr entspricht 165 Minuten und somit
Wasser weniger im See.
Zufluss bis 0 Uhr
Der Zeitraum von 21.15 Uhr bis 0 Uhr entspricht 165 Minuten und somit  Sekunden.
Der Zufluss folgt also mit:
Sekunden.
Der Zufluss folgt also mit:
 Am Ende des Tages befinden sich somit
Am Ende des Tages befinden sich somit  Wasser weniger im Stausee als zu Beginn des Tages.
Wasser weniger im Stausee als zu Beginn des Tages.
3
3.1
3.2
Die Schnittstelle der Funktionen  und
und  beschreibt den Zeitpunkt, an dem die Abflussgeschwindigkeit erstmals größer als die Zuflussgeschwindigkeit ist. An diesem Punkt ist die Füllmenge maximal.
Es soll also gelten:
Mit dem solve-Befehl des CAS folgt:
beschreibt den Zeitpunkt, an dem die Abflussgeschwindigkeit erstmals größer als die Zuflussgeschwindigkeit ist. An diesem Punkt ist die Füllmenge maximal.
Es soll also gelten:
Mit dem solve-Befehl des CAS folgt:
 Nach ungefähr 53 Stunden ist die Füllmenge des Hochwasserschutzraums somit maximal.
Nach ungefähr 53 Stunden ist die Füllmenge des Hochwasserschutzraums somit maximal.
4
4.1
Das Prisma gehört zum Füllgraphen  da es einen eindeutig tiefsten Punkt gibt und das Volumen quadratisch mit der Höhe zunimmt. Beim Zylinder existiert kein eindeutig tiefster Punkt und das Volumen würde linear mit der Höhe zunehmen.
da es einen eindeutig tiefsten Punkt gibt und das Volumen quadratisch mit der Höhe zunimmt. Beim Zylinder existiert kein eindeutig tiefster Punkt und das Volumen würde linear mit der Höhe zunehmen.
4.2
Der Wert kann aus der Abbildung abgelesen werden.
Die Füllhöhe über dem tiefsten Punkt des Sees bei 80 Millionen  beträgt
beträgt 