B2 - Analysis

Das Wachstum einer Hopfenpflanze kann - zergliedert in drei Abschnitte - näherungsweise durch die folgenden Funktionen modelliert werden:

Abschnitt 1: Funktion $h_1$ mit $h_1(t)=0,9 \cdot \mathrm e^{0,022 \cdot t}$ für $0 \leq t \lt63$
Abschnitt 2: Funktion $h_2$ mit $h_2(t)=0,08 \cdot t-1,4$ für $63 \leq t \lt88$
Abschnitt 3: Funktion $h_3$ mit $h_3(t)=8-20 \cdot \mathrm e^{-0,024 \cdot t}$ für $t \geq 88$

Dabei gibt $t$ die Zeit in Tagen nach Auspflanzung des Setzlings an; die Funktionswerte $h_1(t)$ , $h_2(t)$ bzw. $h_3(t)$ geben angenähert die Höhe der Hopfenpflanze in Meter an.

1.1

Ordne zwei der zu den drei Abschnitten gehörenden Funktionen die Begriffe „lineares Wachstum“ und „exponentielles Wachstum“ begründet zu.

Skizziere den Verlauf der Graphen aller drei Funktionen in ihren Definitionsbereichen in ein gemeinsames Koordinatensystem.

(6 BE)

1.2

Gib den Wert $h_1(0)$ an und bestimme den Grenzwert $\lim _{t \rightarrow+\infty} h_3(t).$

Gib die Bedeutung beider Werte im Sachzusammenhang an.

(4 BE)

1.3

Berechne, zu welchem Zeitpunkt die Hopfenpflanze eine Höhe von $7\,\text{m}$ erreicht hat.

Ermittle die mittlere Wachstumsgeschwindigkeit vom Beobachtungsbeginn bis zu diesem Zeitpunkt.

(6 BE)

1.4

Begründe rechnerisch mit Hilfe der Funktionen $h_1, h_2, h_3,$ dass die maximale Wachstumsgeschwindigkeit der Hopfenpflanze im Intervall $[0;200]$ den Wert von $8\, \text{cm}$ pro Tag nicht überschreitet.

(6 BE)

Die Wachstumsgeschwindigkeit einer weiteren Hopfenpflanze kann durch die Funktion $f$ mit $f(t)=\dfrac{85}{976+(t-67,5)^2}$ modelliert werden.

Hierbei gibt $t$ die Zeit in Tagen nach Auspflanzung des Setzlings an; $f(t)$ gibt die Wachstumsgeschwindigkeit in $\dfrac{\text{m}}{\text{Tag}}$ an.

2.1

Begründe, dass der Graph der Funktion $g$ mit $g(t)=\dfrac{85}{976+t^2}$ symmetrisch zur $y$ -Achse ist.

Beschreibe, wie der Graph der Funktion $f$ aus dem Graphen von $g$ hervorgeht.

(4 BE)

2.2

Es sei $F$ eine Stammfunktion der Funktion $f.$

Es gilt $f(t)\gt0$ für alle $t \in \mathbb{R}.$

Erläutere, was dies für die Funktion $F$ bedeutet.

(2 BE)

2.3

Bestimme nur unter Überprüfung der notwendigen Bedingung die Wendestelle der Funktion $F.$

Erläutere die Bedeutung dieser Wendestelle im Sachzusammenhang.

(4 BE)

2.4

Die Hopfenpflanze war zum Zeitpunkt $t=0$ Tage $85 \text{cm}$ hoch.

Exakt 18 Wochen später wird der Hopfen geerntet.

2.4.1

Bestimme die Höhe der Hopfenpflanze zum Zeitpunkt des Erntens.

(4 BE)

2.4.2

Ermittle den Wert des Terms $\dfrac{1}{126} \cdot \displaystyle\int_{0}^{126}f(t)\;\mathrm dt$ und beschreibe die Bedeutung dieses Wertes im Sachzusammenhang.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Begriffe zuordnen

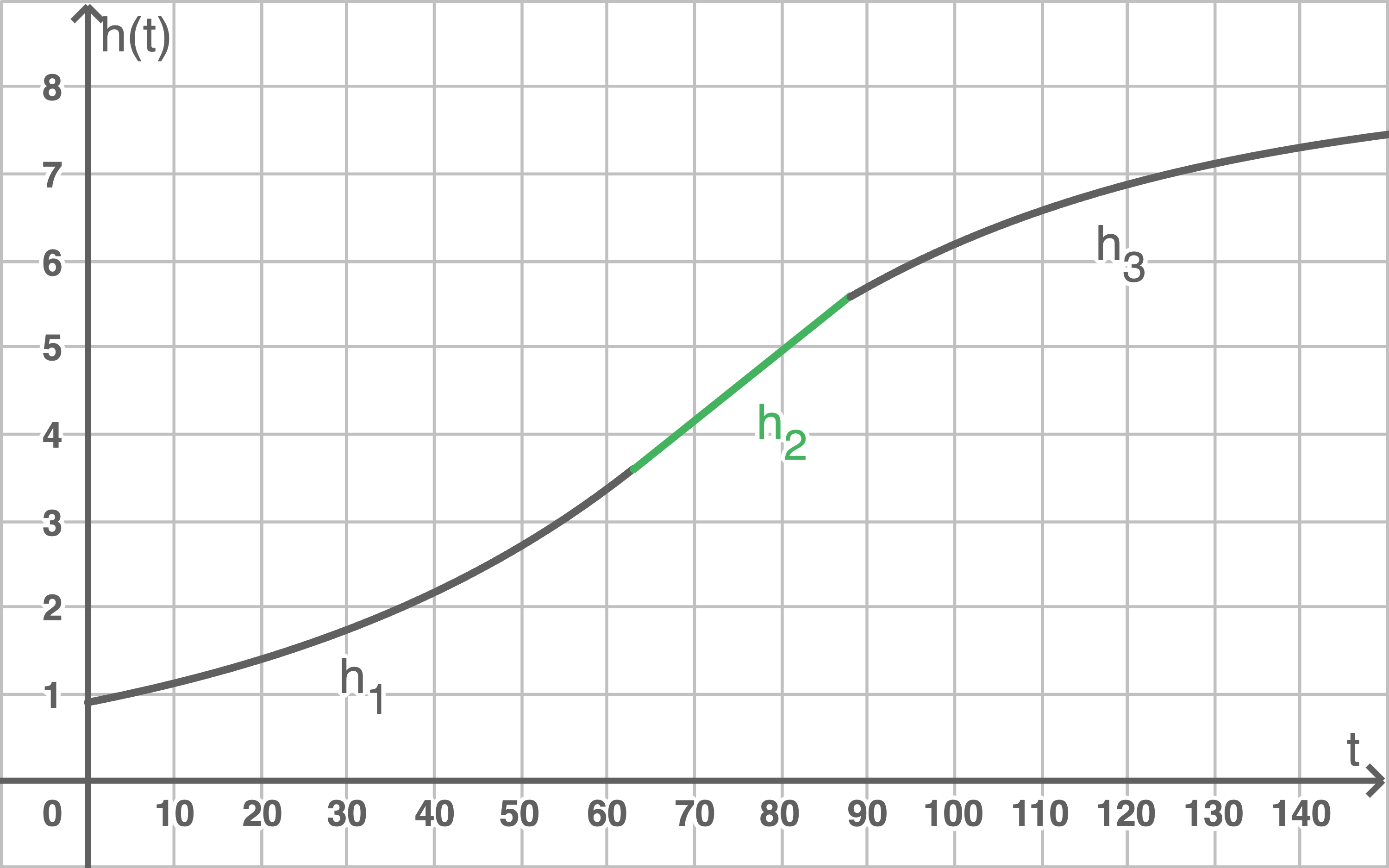
Abschnitt 1: Jeden Tag nimmt die Höhe der Pflanze um den gleichen Faktor $\mathrm e^{0,022}$ zu. Daher handelt es sich bei $h_1$ um exponentielles Wachstum.

Abschnitt 2: Die Steigung von $h_2$ ist konstant mit $m=0,08.$ Jeden Tag nimmt die Höhe der Pflanze um denselben Wert, nämlich um $0,08\,\text{m},$ zu. Es handelt sich bei $h_2$ daher um lineares Wachstum.

Verlauf skizzieren

Mit dem CAS können die einzelnen Graphen dargestellt werden und für die entsprechenden Definitionsbereiche in ein gemeinsames Koordinatensystem übernommen werden:

Wachstum Hopfenpflanze - Hessen Abi 2023

1.2

Wert angeben

$\begin{array}[t]{rll} h_1(0)&=& 0,9 \cdot \mathrm{e}^{0,022 \cdot 0}\ \\[5pt] &=& 0,9 \; [\text{m}] \end{array}$

Grenzwert bestimmen

$\begin{array}[t]{rll} \lim\limits_{t\to\infty}h_3(t)&=& \lim\limits_{t\to\infty}\left(8-20\cdot \mathrm e^{-0,024\cdot t}\right) \\[5pt] &=& 8-20\cdot 0 \\[5pt] &=& 8 \; [\text{m}] \end{array}$

Bedeutung angeben

Der Wert $h_1(0)$ beschreibt die Höhe der Hopfenpflanze zum Zeitpunkt der Auspflanzung des Setzlings. Diese beträgt folglich $0,9\,\text{m}.$

Der Wert $\lim\limits_{t\to\infty}h_3(t)$ beschreibt die Höhe, welcher sich die Hopfenpflanze mit der Zeit annähert. Die Hopfenpflanze wächst somit bis zu einer Höhe von knapp $8\,\text{m}.$

1.3

Zeitpunkt berechnen

Aus der Verlaufsskizze aus Aufgabenteil 1.1 lässt sich ablesen, dass eine Höhe von $7\,\text{m}$ im Definitionsbereich von $h_3$ erreicht wird. Es soll also gelten:

$\begin{array}[t]{rll} h_3(t)&=& 7&\\[5pt] 8-20\cdot \mathrm e^{-0,024t}&=& 7 &\quad \scriptsize \mid\; -8 \\[5pt] -20\cdot \mathrm e^{-0,024t}&=& -1&\quad \scriptsize \mid\; :(-20) \\[5pt] \mathrm e^{-0,024t}&=& 0,05 &\quad \scriptsize \mid\; \ln (\;) \\[5pt] -0,024t&=& \ln(0,05) &\quad \scriptsize \mid\; :-0,024\\[5pt] t&\approx& 124,8 \end{array}$

Die Hopfenpflanze erreicht somit etwa 125 Tage nach Aussetzung des Setzlings eine Höhe von $7\,\text{m}.$

Mittlere Wachstumsgeschwindigkeit bestimmen

$\dfrac{h(124,8)-h(0)}{124,8-0} = \dfrac{7-0,9}{124,8}$ $\approx 0,05 \; \left[ \dfrac{\,\text{m}}{\,\text{Tag}}\right]$

1.4

Die Wachstumsgeschwindigkeit der Pflanze wird durch die Ableitungsfunktionen $\(h_1$ $\(h_2$ und $\(h_3$ beschrieben.

$\(h_1$

$\(h_2$

$\(h_3$

$\boldsymbol{h_1}$ untersuchen

$\(\begin{array}[t]{rll} h_1$

Im Intervall $[0;63[,$ in dem $h_1$ verwendet wird, um die Höhe der Pflanze zu beschreiben überschreitet der Graph von $h_1$ die Steigung von $0,08$ nicht.

$\boldsymbol{h_2}$ untersuchen

$h_2$ wächst linear mit einer Steigung von $0,08.$ Die Pflanze wächst in dem Abschnitt, in dem ihre Höhe durch $h_2$ beschrieben wird also konstant mit einer Wachstumsgeschwindigkeit von $0,08 \dfrac{\,\text{m}}{\,\text{Tag}}= 8 \dfrac{\,\text{cm}}{\,\text{Tag}}$ und überschreitet diese nicht.

$\boldsymbol{h_3}$ untersuchen

$\(\begin{array}[t]{rll} h_3$

Für $t\geq 88$ wird die Wachstumsgeschwindigkeit von $8\,\text{cm}$ pro Tag also ebenfalls nicht überschritten.

2.1

Symmetrie begründen

Ein Graph ist genau dann symmetrisch zur $y$ -Achse, wenn für alle $t$ auf dem Definitionsbereich der Funktion gilt:

$\begin{array}[t]{rll} g(t)&=& g(-t) &\\[5pt] \dfrac{85}{976+t^2}&=& \dfrac{85}{976+(-t)^2} &\\[5pt] \end{array}$

Wegen $t^2=(-t)^2$ folgt also, dass der Graph der Funktion $g$ symmerisch zur $y$ -Achse ist.

Beschreibung

Der Graph der Funktion $f$ geht durch Verschiebung um $67,5$ Längeneinheiten in positive $x$ -Richtung aus dem Graphen von $g$ hervor.

2.2

Da $f(t)$ stets positiv ist gilt somit auch, dass die Ableitung $\(F$ der Stammfunktion $F(t)$ immer positiv ist.

$F$ steigt folglich streng monoton und der zugehörige Graph besitzt weder Hoch- noch Tiefpunkte.

2.3

Wendestelle bestimmen

Ableitungen bestimmen:

$\(\begin{array}[t]{rll} F$

$\( F$

Zweite Ableitung anzeigen

Notwendige Bedingung für Wendestellen anwenden:

Rechnung anzeigen

$t=67,5$

Die Wendestelle der Funktion $F$ ist somit gegeben durch $t=67,5.$

Bedeutung erläutern

Die Wendestelle der Funktion $F$ entspricht der Extremstelle von $\(F$ und somit von $f.$

Sie gibt somit den Zeitpunkt nach Auspflanzung des Setzlings an, zu welchem die Wachstumgsgeschwindigkeit der Hopfenpflanze maximal oder minimal ist.

2.4.1

18 Wochen entsprechen $18\cdot 7=126$ Tagen.

Somit gilt für die Höhe der Hopfenpflanze zum Zeitpunkt der Ernte:

$0,85+\displaystyle\int_{0}^{126}f(t)\;\mathrm dt \approx 6,88 \; [\text{m}]$

Rechenweg anzeigen

2.4.2

Wert ermitteln

$\begin{array}[t]{rll} \dfrac{1}{126}\cdot \displaystyle\int_{0}^{126}f(t)\;\mathrm dt &=& \dfrac{1}{126}\cdot 6,03 & \\[5pt] &\approx& 0,048 \end{array}$

Bedeutung beschreiben

Die Hopfenpflanze wächst durchschnittlich ca. $4,8\,\text{cm}$ pro Tag.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?