B2 - Analytische Geometrie
Auf dem Rasen eines Fußballstadions soll eine Bühne für eine Kundgebung aufgebaut werden. Der verantwortliche Architekt legt für die Planung ein dreidimensionales kartesisches Koordinatensystem an. Die Rasenfläche liegt in der  -Ebene. Die
-Ebene. Die  -Achse zeigt senkrecht zur
-Achse zeigt senkrecht zur  -Ebene in Richtung des Betrachters. Im grau unterlegten Bereich wird ein Bühnenboden errichtet, der sich
-Ebene in Richtung des Betrachters. Im grau unterlegten Bereich wird ein Bühnenboden errichtet, der sich  über dem Rasen befindet (Abbildung 1).
Alle in der Skizze eingetragenen Zahlenwerte sind in der Einheit Meter angegeben.
über dem Rasen befindet (Abbildung 1).
Alle in der Skizze eingetragenen Zahlenwerte sind in der Einheit Meter angegeben.
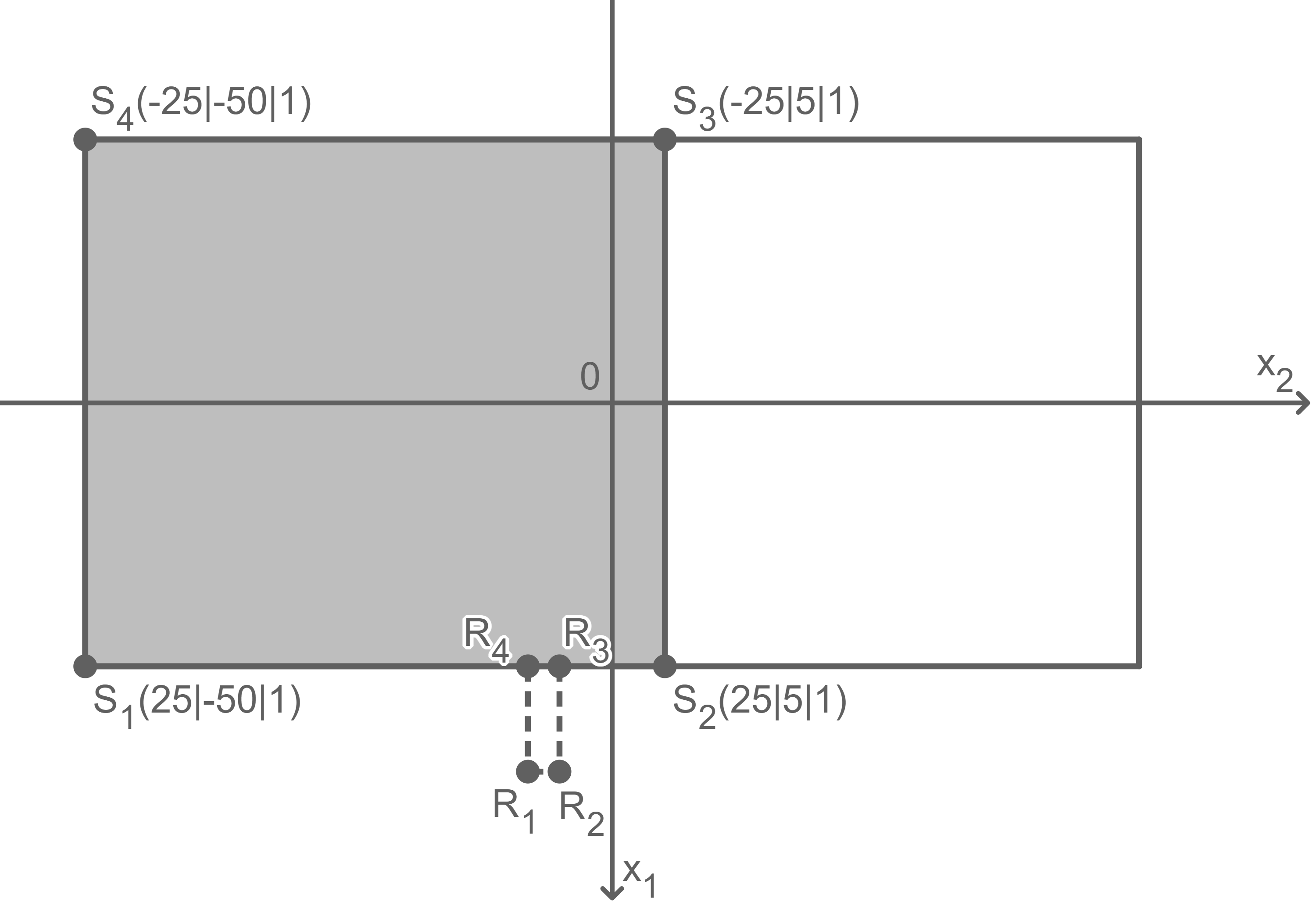
Abbildung 1
1
Um leichter auf den Bühnenboden zu gelangen, soll eine  breite Rampe mit rechteckigem Grundriss gebaut und in
breite Rampe mit rechteckigem Grundriss gebaut und in  und
und  verankert werden.
verankert werden.
1.1
Gib die Koordinaten der Eckpunkte  und
und  an und berechne die Länge der Rampe.
an und berechne die Länge der Rampe.
(5 BE)
1.2
Nach DIN 18024-1 darf der Steigungswinkel einer barrierefreien Rampe maximal  betragen.
Berechne den Steigungswinkel der Rampe und entscheide, ob diese die DIN erfüllt.
betragen.
Berechne den Steigungswinkel der Rampe und entscheide, ob diese die DIN erfüllt.
Mit Seilen soll über dem Fußballplatz eine dreieckige Fläche aus Segeltuch gespannt werden. Zwei der drei Eckpunkte dieses Dreiecks liegen in
(4 BE)
2
Der dritte Eckpunkt  ist ein variabler Punkt auf dem Seil, welches von
ist ein variabler Punkt auf dem Seil, welches von  zur Spitze des Flutlichtmastes
zur Spitze des Flutlichtmastes  gespannt wird.
gespannt wird.
2.1
Zeige, dass im Dreieck  bei
bei  ein rechter Winkel vorliegt.
Erläutere, dass das Dreieck
ein rechter Winkel vorliegt.
Erläutere, dass das Dreieck  immer rechtwinklig ist - egal, wo sich der Punkt
immer rechtwinklig ist - egal, wo sich der Punkt  auf dem Seil zwischen
auf dem Seil zwischen  und
und  befindet.
befindet.
(5 BE)
2.2
Das Segeltuch, mit dem das Dreieck  bespannt werden soll, darf aus Gewichtsgründen höchstens
bespannt werden soll, darf aus Gewichtsgründen höchstens  groß sein.
Bestimme die Koordinaten des Punktes
groß sein.
Bestimme die Koordinaten des Punktes  auf dem Seil, für den die Dreiecksfläche die zugelassene Maximalgröße hat.
auf dem Seil, für den die Dreiecksfläche die zugelassene Maximalgröße hat.
(6 BE)
3
Das Segeltuch wird bei  fixiert und straff gespannt. Zu einer gewissen Uhrzeit fallen Sonnenstrahlen in Richtung
fixiert und straff gespannt. Zu einer gewissen Uhrzeit fallen Sonnenstrahlen in Richtung  ein, so dass das Segeltuch einen dreieckigen Schatten auf den geplanten Bühnenboden wirft.
Die Schattenpunkte der Punkte
ein, so dass das Segeltuch einen dreieckigen Schatten auf den geplanten Bühnenboden wirft.
Die Schattenpunkte der Punkte  und
und  liegen bei
liegen bei  und
und  .
.
3.1
Berechne die Koordinaten des Schattenpunktes  des Punktes
des Punktes  auf dem Bühnenboden.
auf dem Bühnenboden.
(5 BE)
3.2
Im Punkt  soll ein Mikrofon aufgestellt werden.
Zeichne unter Angabe einer geeigneten Skalierung der Achsen den Schatten des Segeltuchs in das Koordinatensystem in Abbildung 2 ein.
Prüfe zeichnerisch, ob der Fußpunkt
soll ein Mikrofon aufgestellt werden.
Zeichne unter Angabe einer geeigneten Skalierung der Achsen den Schatten des Segeltuchs in das Koordinatensystem in Abbildung 2 ein.
Prüfe zeichnerisch, ob der Fußpunkt  des Mikrofonstativs im Schatten liegt.
Falls Aufgabe 3.1 nicht gelöst wurde, kann der Ersatzpunkt
des Mikrofonstativs im Schatten liegt.
Falls Aufgabe 3.1 nicht gelöst wurde, kann der Ersatzpunkt  verwendet werden.
verwendet werden.
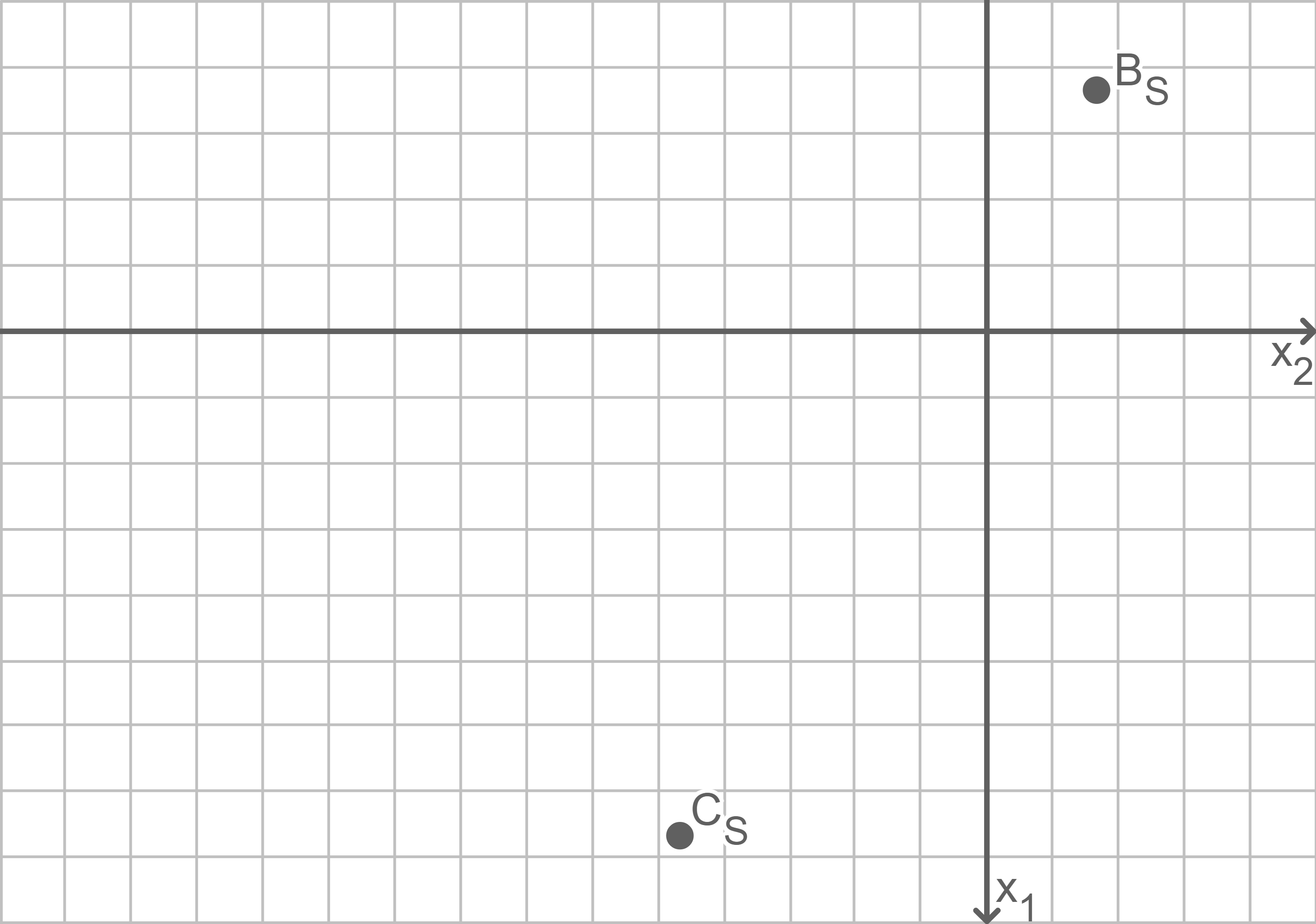
Abbildung 2
(5 BE)
1.1
Koordinaten angeben
Da die Rampe 3 Meter breit sein soll, folgen die Koordinaten mit:

 Länge berechnen
Eine Seite der Rampe wird durch den Vektor
Länge berechnen
Eine Seite der Rampe wird durch den Vektor  dargestellt.
Es gilt also:
dargestellt.
Es gilt also:
![\(\begin{array}[t]{rll}
\left| \overrightarrow{R_2R_3}\right|&=& \left| \pmatrix{10\\0\\-1} \right|& \\[5pt]
&=& \sqrt{10^2+(-1)^2} & \\[5pt]
&=& \sqrt{101}& \\[5pt]
&\approx& 10,05 \; [\,\text{m}]
\end{array}\)](https://mathjax.schullv.de/7c2d8016a1b079263c3453a56e7f9fbd8a938ad7f12eefe7f6d92f08336329a0?color=5a5a5a) Die Rampe ist somit ca. 10,05 Meter lang.
Die Rampe ist somit ca. 10,05 Meter lang.
1.2
Steigungswinkel berechnen
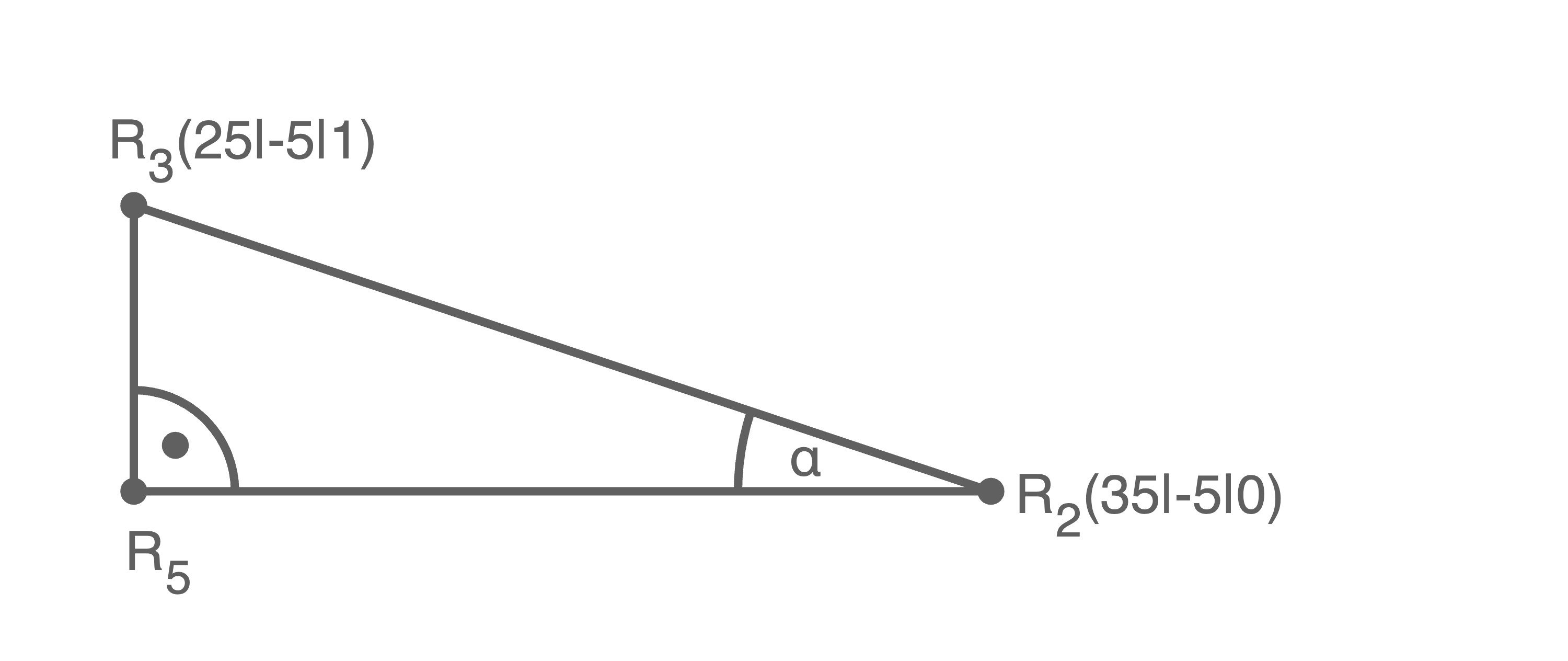
 Hilfsskizze (nicht maßstäblich)
Der Steigungswinkel der Rampe beträgt folglich
Hilfsskizze (nicht maßstäblich)
Der Steigungswinkel der Rampe beträgt folglich  Entscheidung
Da der Steigungswinkel einer barrierefreien Rampe maximal
Entscheidung
Da der Steigungswinkel einer barrierefreien Rampe maximal  betragen darf und der Steigungswinkel der Rampe in der Aufgabe
betragen darf und der Steigungswinkel der Rampe in der Aufgabe  beträgt, wird diese DIN nicht erfüllt.
beträgt, wird diese DIN nicht erfüllt.
Um den Steigungswinkel  berechnen zu können, werden zwei Seiten des Dreiecks benötigt. Da der Punkt
berechnen zu können, werden zwei Seiten des Dreiecks benötigt. Da der Punkt  senkrecht unter dem Punkt
senkrecht unter dem Punkt  liegt, besitzt er die Koordinaten
liegt, besitzt er die Koordinaten  Somit folgt der Steigungswinkel mit:
Somit folgt der Steigungswinkel mit:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\text{Gegenkathete}}{\text{Hypothenuse}} &\\[5pt]
\sin(\alpha)&=& \dfrac{\left| \overrightarrow{R_3R_5} \right|}{\left| \overrightarrow{R_2R_3}\right|} & \\[5pt]
\sin(\alpha)&=& \dfrac{\left| \pmatrix{0\\0\\-1} \right|}{\left| \pmatrix{-10\\0\\1} \right|}&\\[5pt]
\sin(\alpha)&=& \dfrac{\sqrt{(-1)^2}}{\sqrt{(-10)^2+1^2}} &\\[5pt]
\sin(\alpha)&\approx& 0,0995 &\quad \scriptsize \mid\; \sin^{-1}\\[5pt]
\alpha&\approx& 5,71^\circ
\end{array}\)](https://mathjax.schullv.de/a2755a9312f3282fc13d2a4116d69c281a21c7b5392eb82242f8036d454676a0?color=5a5a5a)

2.1
Rechten Winkel nachweisen
Ein rechter Winkel bei  liegt genau dann vor, wenn die beiden Verbindungsvektoren
liegt genau dann vor, wenn die beiden Verbindungsvektoren  und
und  orthogonal zueinander stehen, d.h. wenn das Skalarprodukt der Vektoren Null ergibt.
Verbindungsvektoren bestimmen:
orthogonal zueinander stehen, d.h. wenn das Skalarprodukt der Vektoren Null ergibt.
Verbindungsvektoren bestimmen:

 Das Skalarprodukt der Vektoren
Das Skalarprodukt der Vektoren  und
und  kann mit Hilfe des dotP()-Befehls des CAS berechnet werden. Dieser kann unter 7: Matrix und Vektor
kann mit Hilfe des dotP()-Befehls des CAS berechnet werden. Dieser kann unter 7: Matrix und Vektor  C
C  3 gefunden werden.
3 gefunden werden.
 Da das Skalarprodukt Null ergibt und die Vektoren
Da das Skalarprodukt Null ergibt und die Vektoren  und
und  somit orthogonal zueinander stehen, liegt bei Punkt
somit orthogonal zueinander stehen, liegt bei Punkt  ein rechter Winkel vor.
Erläuterung
Die unterschiedliche Position von
ein rechter Winkel vor.
Erläuterung
Die unterschiedliche Position von  auf
auf  verkürzt den Vektor, ändert aber nicht seine Richtung.
Damit bleibt der rechte Winkel bei
verkürzt den Vektor, ändert aber nicht seine Richtung.
Damit bleibt der rechte Winkel bei  erhalten.
Mathematisch lässt sich das durch das Einführen eines Parameters
erhalten.
Mathematisch lässt sich das durch das Einführen eines Parameters  zeigen, der die Länge des Vektors variieren lässt.
Mit dem Verbindungsvektor
zeigen, der die Länge des Vektors variieren lässt.
Mit dem Verbindungsvektor  gilt für das Skalarprodukt:
gilt für das Skalarprodukt:
![\(\begin{array}[t]{rll}
\overrightarrow{AC}\circ\overrightarrow{AB}&=& \pmatrix{30r\\40r\\10r} \circ \pmatrix{-3\\4\\-7}& \\[5pt]
&=& -90r+160r-70r&\\[5pt]
&=& 0
\end{array}\)](https://mathjax.schullv.de/0c7d8125c384589d689d9a103c604610db26e5983c62749278a73fce162ba733?color=5a5a5a) Somit ist das Skalarprodukt eines beliebig langen Vektors
Somit ist das Skalarprodukt eines beliebig langen Vektors  mit
mit  Null, sodass der rechte Winkel bei
Null, sodass der rechte Winkel bei  unabhängig von der Position von
unabhängig von der Position von  auf
auf  existiert.
existiert.

2.2
Da es sich bei dem Dreieck  um ein rechtwinkliges Dreieck handelt, kann der Flächeninhalt wie folgt bestimmt werden:
um ein rechtwinkliges Dreieck handelt, kann der Flächeninhalt wie folgt bestimmt werden:
![\(\begin{array}[t]{rll}
A_{ABC}&=& \dfrac{1}{2}\cdot|\overrightarrow{AB}|\cdot|\overrightarrow{AC}|&\\[5pt]
&=& \dfrac{1}{2}\cdot|\overrightarrow{AB}|\cdot r\cdot|\overrightarrow{AP}|
\end{array}\)](https://mathjax.schullv.de/5190a75e363102928c5daec655112b0b19d631fa95b27a8d9a15488796163cee?color=5a5a5a) Längen der Vektoren berechnen:
Längen der Vektoren berechnen:
![\(\begin{array}[t]{rll}
|\overrightarrow{AB}|&=& \left|\pmatrix{-3\\4\\-7} \right| & \\[5pt]
&=& \sqrt{(-3)^2+4^2+(-7)^2} & \\[5pt]
&\approx & 8,6 \;[\,\text{m}]
\end{array}\)](https://mathjax.schullv.de/3a32d3f65373bb0d058d86f20e2dbbf4f8b596a6ec78cfbb376afeabf8e9a99e?color=5a5a5a)
![\(\begin{array}[t]{rll}
|\overrightarrow{AP}|&=& \left| \pmatrix{30\\40\\10} \right| & \\[5pt]
&=& \sqrt{30^2+40^2+10^2} & \\[5pt]
&\approx& 50,99 \;[\,\text{m}]
\end{array}\)](https://mathjax.schullv.de/b4e55d5ed9ab0a2946cf1d1ba5b547f56b54d385c82420d29282bbf48c4482cd?color=5a5a5a) Alternativ können die Beträge der Vektoren mit dem CAS unter dem dotP()-Befehl berechnet werden. Dieser kann durch 7: Matrix und Vektor
Alternativ können die Beträge der Vektoren mit dem CAS unter dem dotP()-Befehl berechnet werden. Dieser kann durch 7: Matrix und Vektor  C
C  3 gefunden werden.
3 gefunden werden.
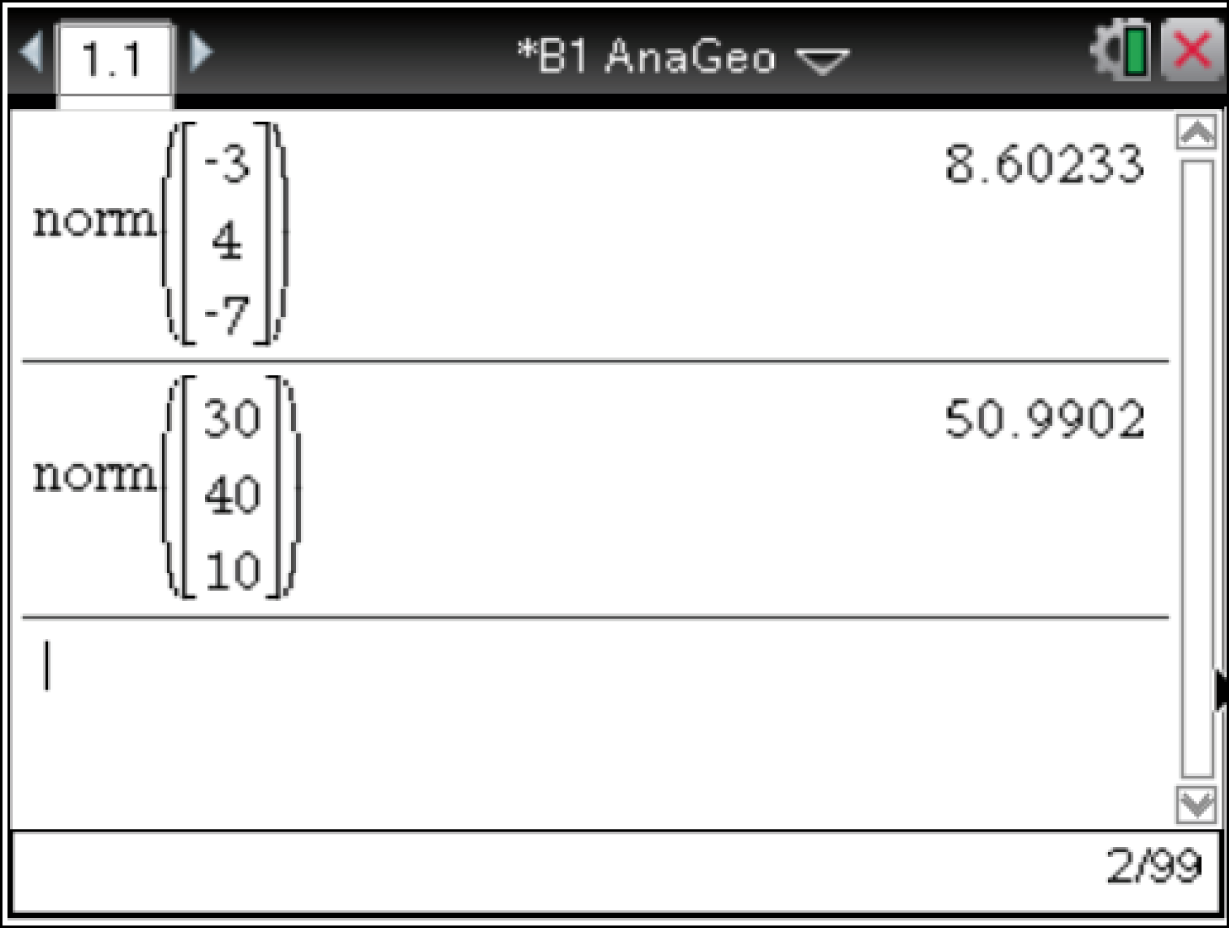 Für die zugelassene Maximalgröße gilt:
Für die zugelassene Maximalgröße gilt:
![\(\begin{array}[t]{rll}
A_{ABC}&=& 100 & \\[5pt]
\dfrac{1}{2}\cdot|\overrightarrow{AB}|\cdot r\cdot|\overrightarrow{AP}|&=& 100& \\[5pt]
\dfrac{1}{2}\cdot 8,6 \cdot r\cdot 50,99&=& 100 & \\[5pt]
219,257\cdot r&=& 100 &\quad \scriptsize \mid\;:219,257 \\[5pt]
r&\approx& 0,46
\end{array}\)](https://mathjax.schullv.de/46a033fa9f013e323701bdcd3f61c4ed8b8cdf7ee014188ca0bf472d9a6c0c1b?color=5a5a5a) Die Koordinaten von Punkt
Die Koordinaten von Punkt  ergeben sich somit zu:
ergeben sich somit zu:
![\(\begin{array}[t]{rll}
\overrightarrow{OC}&=& \overrightarrow{OA}+r\cdot\overrightarrow{AP}& \\[5pt]
&=& \pmatrix{5\\26\\25}+0,46\cdot \pmatrix{30\\40\\10}& \\[5pt]
&=& \pmatrix{18,8\\44,4\\29,6}& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/43384f13d76f1e4683f0f040f27275ca3bc792a4944e28e29c150f5175589058?color=5a5a5a) Damit die Dreiecksfläche die zugelassene Maximalgröße hat, muss der Punkt
Damit die Dreiecksfläche die zugelassene Maximalgröße hat, muss der Punkt  auf dem Seil die Koordinaten
auf dem Seil die Koordinaten  besitzen.
besitzen.

3.1
Der Schattenpunkt  auf der Bühnenebene entspricht dem Schnittpunkt der Geraden durch
auf der Bühnenebene entspricht dem Schnittpunkt der Geraden durch  mit dem Richtungsvektor
mit dem Richtungsvektor  und der Bühne.
Da die Bühne in einer Höhe von 1 m aufgebaut wurde und parallel zur
und der Bühne.
Da die Bühne in einer Höhe von 1 m aufgebaut wurde und parallel zur  -Ebene ist, liegt sie folglich in der Ebenen mit der Koordinatengleichung
-Ebene ist, liegt sie folglich in der Ebenen mit der Koordinatengleichung  Der Schattenpunkt
Der Schattenpunkt  besitzt somit ebenso die
besitzt somit ebenso die  -Kooordinate
-Kooordinate  Die Geradengleichung durch den Punkt
Die Geradengleichung durch den Punkt  mit dem Richtungsvektor
mit dem Richtungsvektor  ergibt sich zu:
ergibt sich zu:
![\(\begin{array}[t]{rll}
g: \overrightarrow{x}&=& \overrightarrow{OA}+s\cdot\vec{v}& \\[5pt]
&=& \pmatrix{5\\26\\25} +s\cdot \pmatrix{-1\\-5\\-3}
\end{array}\)](https://mathjax.schullv.de/959e15c85d8effff39c6903baa952a83520d9f85e8f376a62166e82585f49a35?color=5a5a5a) Für den Schattenpunkt
Für den Schattenpunkt  gilt:
gilt:
![\(\begin{array}[t]{rll}
x_3&=& 1&\\[5pt]
25-3\cdot s&=& 1&\quad \scriptsize \mid\;-25 \\[5pt]
-3\cdot s&=& -24&\quad \scriptsize \mid\; :(-3)\\[5pt]
s&=& 8
\end{array}\)](https://mathjax.schullv.de/835b488e4a809e40ec96763d970634f07cce5da3c0a63ee48850ba55b10e9bcf?color=5a5a5a) Einsetzen von
Einsetzen von  in die Geradengleichung liefert:
in die Geradengleichung liefert:
![\(\begin{array}[t]{rll}
\overrightarrow{OA_S}&=& \pmatrix{5\\26\\25} +8 \cdot \pmatrix{-1\\-5\\-3}&\\[5pt]
&=& \pmatrix{-3\\-14\\1}
\end{array}\)](https://mathjax.schullv.de/1ada6ffd212e675e08c18e1880030ad449a75e3140a51b3349527f8adcb39b69?color=5a5a5a) Der Schattenpunkt
Der Schattenpunkt  auf dem Bühnenboden besitzt somit die Koordinaten
auf dem Bühnenboden besitzt somit die Koordinaten 
3.2
Beim Skalieren ist zu beachten, dass die  -Achse nach unten zeigt und somit unterhalb der
-Achse nach unten zeigt und somit unterhalb der  -Achse positive Werte annimmt.
Die
-Achse positive Werte annimmt.
Die  -Achse weist aus der Zeichenebene heraus und wird somit in der Skizze vernachlässigt.
-Achse weist aus der Zeichenebene heraus und wird somit in der Skizze vernachlässigt.
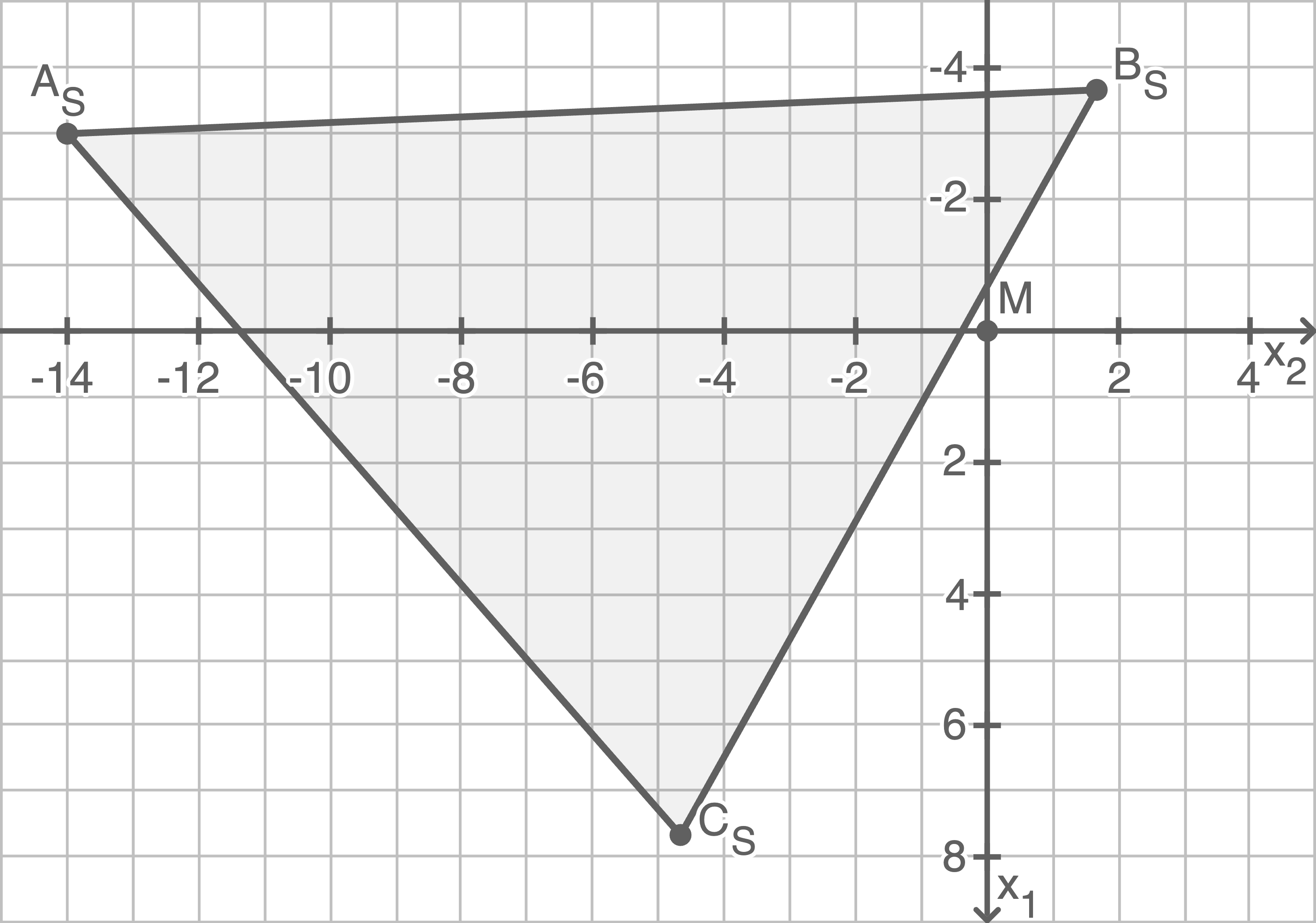 Aus der Abbildung geht hervor, dass der Fußpunkt
Aus der Abbildung geht hervor, dass der Fußpunkt  des Mikrofonstativs nicht im Schatten liegt.
des Mikrofonstativs nicht im Schatten liegt.

1.1
Koordinaten angeben
Da die Rampe 3 Meter breit sein soll, folgen die Koordinaten mit:

 Länge berechnen
Eine Seite der Rampe wird durch den Vektor
Länge berechnen
Eine Seite der Rampe wird durch den Vektor  dargestellt.
Es gilt also:
dargestellt.
Es gilt also:
![\(\begin{array}[t]{rll}
\left| \overrightarrow{R_2R_3}\right|&=& \left| \pmatrix{10\\0\\-1} \right|& \\[5pt]
&=& \sqrt{10^2+(-1)^2} & \\[5pt]
&=& \sqrt{101}& \\[5pt]
&\approx& 10,05 \; [\,\text{m}]
\end{array}\)](https://mathjax.schullv.de/7c2d8016a1b079263c3453a56e7f9fbd8a938ad7f12eefe7f6d92f08336329a0?color=5a5a5a) Die Rampe ist somit ca. 10,05 Meter lang.
Die Rampe ist somit ca. 10,05 Meter lang.
1.2
Steigungswinkel berechnen

 Hilfsskizze (nicht maßstäblich)
Der Steigungswinkel der Rampe beträgt folglich
Hilfsskizze (nicht maßstäblich)
Der Steigungswinkel der Rampe beträgt folglich  Entscheidung
Da der Steigungswinkel einer barrierefreien Rampe maximal
Entscheidung
Da der Steigungswinkel einer barrierefreien Rampe maximal  betragen darf und der Steigungswinkel der Rampe in der Aufgabe
betragen darf und der Steigungswinkel der Rampe in der Aufgabe  beträgt, wird diese DIN nicht erfüllt.
beträgt, wird diese DIN nicht erfüllt.
Um den Steigungswinkel  berechnen zu können, werden zwei Seiten des Dreiecks benötigt. Da der Punkt
berechnen zu können, werden zwei Seiten des Dreiecks benötigt. Da der Punkt  senkrecht unter dem Punkt
senkrecht unter dem Punkt  liegt, besitzt er die Koordinaten
liegt, besitzt er die Koordinaten  Somit folgt der Steigungswinkel mit:
Somit folgt der Steigungswinkel mit:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\text{Gegenkathete}}{\text{Hypothenuse}} &\\[5pt]
\sin(\alpha)&=& \dfrac{\left| \overrightarrow{R_3R_5} \right|}{\left| \overrightarrow{R_2R_3}\right|} & \\[5pt]
\sin(\alpha)&=& \dfrac{\left| \pmatrix{0\\0\\-1} \right|}{\left| \pmatrix{-10\\0\\1} \right|}&\\[5pt]
\sin(\alpha)&=& \dfrac{\sqrt{(-1)^2}}{\sqrt{(-10)^2+1^2}} &\\[5pt]
\sin(\alpha)&\approx& 0,0995 &\quad \scriptsize \mid\; \sin^{-1}\\[5pt]
\alpha&\approx& 5,71^\circ
\end{array}\)](https://mathjax.schullv.de/a2755a9312f3282fc13d2a4116d69c281a21c7b5392eb82242f8036d454676a0?color=5a5a5a)

2.1
Rechten Winkel nachweisen
Ein rechter Winkel bei  liegt genau dann vor, wenn die beiden Verbindungsvektoren
liegt genau dann vor, wenn die beiden Verbindungsvektoren  und
und  orthogonal zueinander stehen, d.h. wenn das Skalarprodukt der Vektoren Null ergibt.
Verbindungsvektoren bestimmen:
orthogonal zueinander stehen, d.h. wenn das Skalarprodukt der Vektoren Null ergibt.
Verbindungsvektoren bestimmen:

 Das Skalarprodukt der Vektoren
Das Skalarprodukt der Vektoren  und
und  kann mit Hilfe des dotP()-Befehls des CAS berechnet werden. Dieser kann unter Interactive
kann mit Hilfe des dotP()-Befehls des CAS berechnet werden. Dieser kann unter Interactive  Vector
Vector  dotP gefunden werden.
dotP gefunden werden.
 Da das Skalarprodukt Null ergibt und die Vektoren
Da das Skalarprodukt Null ergibt und die Vektoren  und
und  somit orthogonal zueinander stehen, liegt bei Punkt
somit orthogonal zueinander stehen, liegt bei Punkt  ein rechter Winkel vor.
Erläuterung
Die unterschiedliche Position von
ein rechter Winkel vor.
Erläuterung
Die unterschiedliche Position von  auf
auf  verkürzt den Vektor, ändert aber nicht seine Richtung.
Damit bleibt der rechte Winkel bei
verkürzt den Vektor, ändert aber nicht seine Richtung.
Damit bleibt der rechte Winkel bei  erhalten.
Mathematisch lässt sich das durch das Einführen eines Parameters
erhalten.
Mathematisch lässt sich das durch das Einführen eines Parameters  zeigen, der die Länge des Vektors variieren lässt.
Mit dem Verbindungsvektor
zeigen, der die Länge des Vektors variieren lässt.
Mit dem Verbindungsvektor  gilt für das Skalarprodukt:
gilt für das Skalarprodukt:
![\(\begin{array}[t]{rll}
\overrightarrow{AC}\circ\overrightarrow{AB}&=& \pmatrix{30r\\40r\\10r} \circ \pmatrix{-3\\4\\-7}& \\[5pt]
&=& -90r+160r-70r&\\[5pt]
&=& 0
\end{array}\)](https://mathjax.schullv.de/0c7d8125c384589d689d9a103c604610db26e5983c62749278a73fce162ba733?color=5a5a5a) Somit ist das Skalarprodukt eines beliebig langen Vektors
Somit ist das Skalarprodukt eines beliebig langen Vektors  mit
mit  Null, sodass der rechte Winkel bei
Null, sodass der rechte Winkel bei  unabhängig von der Position von
unabhängig von der Position von  auf
auf  existiert.
existiert.

2.2
Da es sich bei dem Dreieck  um ein rechtwinkliges Dreieck handelt, kann der Flächeninhalt wie folgt bestimmt werden:
um ein rechtwinkliges Dreieck handelt, kann der Flächeninhalt wie folgt bestimmt werden:
![\(\begin{array}[t]{rll}
A_{ABC}&=& \dfrac{1}{2}\cdot|\overrightarrow{AB}|\cdot|\overrightarrow{AC}|&\\[5pt]
&=& \dfrac{1}{2}\cdot|\overrightarrow{AB}|\cdot r\cdot|\overrightarrow{AP}|
\end{array}\)](https://mathjax.schullv.de/5190a75e363102928c5daec655112b0b19d631fa95b27a8d9a15488796163cee?color=5a5a5a) Längen der Vektoren berechnen:
Längen der Vektoren berechnen:
![\(\begin{array}[t]{rll}
|\overrightarrow{AB}|&=& \left|\pmatrix{-3\\4\\-7} \right| & \\[5pt]
&=& \sqrt{(-3)^2+4^2+(-7)^2} & \\[5pt]
&\approx & 8,6 \;[\,\text{m}]
\end{array}\)](https://mathjax.schullv.de/3a32d3f65373bb0d058d86f20e2dbbf4f8b596a6ec78cfbb376afeabf8e9a99e?color=5a5a5a)
![\(\begin{array}[t]{rll}
|\overrightarrow{AP}|&=& \left| \pmatrix{30\\40\\10} \right| & \\[5pt]
&=& \sqrt{30^2+40^2+10^2} & \\[5pt]
&\approx& 50,99 \;[\,\text{m}]
\end{array}\)](https://mathjax.schullv.de/b4e55d5ed9ab0a2946cf1d1ba5b547f56b54d385c82420d29282bbf48c4482cd?color=5a5a5a) Alternativ können die Beträge der Vektoren mit dem CAS unter dem dotP()-Befehl berechnet werden. Dieser kann durch Interactive
Alternativ können die Beträge der Vektoren mit dem CAS unter dem dotP()-Befehl berechnet werden. Dieser kann durch Interactive  Matrix-Calc
Matrix-Calc  norm gefunden werden.
norm gefunden werden.
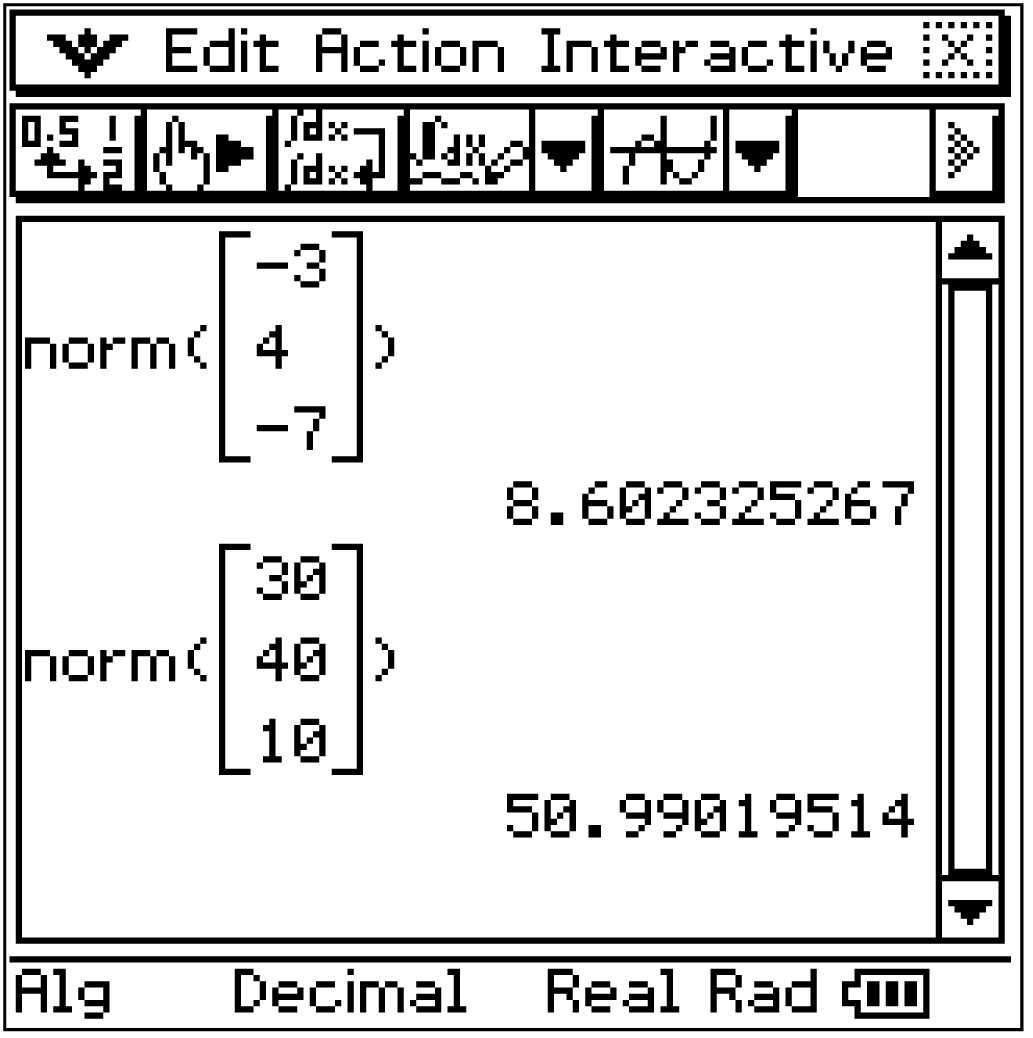 Für die zugelassene Maximalgröße gilt:
Für die zugelassene Maximalgröße gilt:
![\(\begin{array}[t]{rll}
A_{ABC}&=& 100 & \\[5pt]
\dfrac{1}{2}\cdot|\overrightarrow{AB}|\cdot r\cdot|\overrightarrow{AP}|&=& 100& \\[5pt]
\dfrac{1}{2}\cdot 8,6 \cdot r\cdot 50,99&=& 100 & \\[5pt]
219,257\cdot r&=& 100 &\quad \scriptsize \mid\;:219,257 \\[5pt]
r&\approx& 0,46
\end{array}\)](https://mathjax.schullv.de/46a033fa9f013e323701bdcd3f61c4ed8b8cdf7ee014188ca0bf472d9a6c0c1b?color=5a5a5a) Die Koordinaten von Punkt
Die Koordinaten von Punkt  ergeben sich somit zu:
ergeben sich somit zu:
![\(\begin{array}[t]{rll}
\overrightarrow{OC}&=& \overrightarrow{OA}+r\cdot\overrightarrow{AP}& \\[5pt]
&=& \pmatrix{5\\26\\25}+0,46\cdot \pmatrix{30\\40\\10}& \\[5pt]
&=& \pmatrix{18,8\\44,4\\29,6}& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/43384f13d76f1e4683f0f040f27275ca3bc792a4944e28e29c150f5175589058?color=5a5a5a) Damit die Dreiecksfläche die zugelassene Maximalgröße hat, muss der Punkt
Damit die Dreiecksfläche die zugelassene Maximalgröße hat, muss der Punkt  auf dem Seil die Koordinaten
auf dem Seil die Koordinaten  besitzen.
besitzen.

3.1
Der Schattenpunkt  auf der Bühnenebene entspricht dem Schnittpunkt der Geraden durch
auf der Bühnenebene entspricht dem Schnittpunkt der Geraden durch  mit dem Richtungsvektor
mit dem Richtungsvektor  und der Bühne.
Da die Bühne in einer Höhe von 1 m aufgebaut wurde und parallel zur
und der Bühne.
Da die Bühne in einer Höhe von 1 m aufgebaut wurde und parallel zur  -Ebene ist, liegt sie folglich in der Ebenen mit der Koordinatengleichung
-Ebene ist, liegt sie folglich in der Ebenen mit der Koordinatengleichung  Der Schattenpunkt
Der Schattenpunkt  besitzt somit ebenso die
besitzt somit ebenso die  -Kooordinate
-Kooordinate  Die Geradengleichung durch den Punkt
Die Geradengleichung durch den Punkt  mit dem Richtungsvektor
mit dem Richtungsvektor  ergibt sich zu:
ergibt sich zu:
![\(\begin{array}[t]{rll}
g: \overrightarrow{x}&=& \overrightarrow{OA}+s\cdot\vec{v}& \\[5pt]
&=& \pmatrix{5\\26\\25} +s\cdot \pmatrix{-1\\-5\\-3}
\end{array}\)](https://mathjax.schullv.de/959e15c85d8effff39c6903baa952a83520d9f85e8f376a62166e82585f49a35?color=5a5a5a) Für den Schattenpunkt
Für den Schattenpunkt  gilt:
gilt:
![\(\begin{array}[t]{rll}
x_3&=& 1&\\[5pt]
25-3\cdot s&=& 1&\quad \scriptsize \mid\;-25 \\[5pt]
-3\cdot s&=& -24&\quad \scriptsize \mid\; :(-3)\\[5pt]
s&=& 8
\end{array}\)](https://mathjax.schullv.de/835b488e4a809e40ec96763d970634f07cce5da3c0a63ee48850ba55b10e9bcf?color=5a5a5a) Einsetzen von
Einsetzen von  in die Geradengleichung liefert:
in die Geradengleichung liefert:
![\(\begin{array}[t]{rll}
\overrightarrow{OA_S}&=& \pmatrix{5\\26\\25} +8 \cdot \pmatrix{-1\\-5\\-3}&\\[5pt]
&=& \pmatrix{-3\\-14\\1}
\end{array}\)](https://mathjax.schullv.de/1ada6ffd212e675e08c18e1880030ad449a75e3140a51b3349527f8adcb39b69?color=5a5a5a) Der Schattenpunkt
Der Schattenpunkt  auf dem Bühnenboden besitzt somit die Koordinaten
auf dem Bühnenboden besitzt somit die Koordinaten 
3.2
Beim Skalieren ist zu beachten, dass die  -Achse nach unten zeigt und somit unterhalb der
-Achse nach unten zeigt und somit unterhalb der  -Achse positive Werte annimmt.
Die
-Achse positive Werte annimmt.
Die  -Achse weist aus der Zeichenebene heraus und wird somit in der Skizze vernachlässigt.
-Achse weist aus der Zeichenebene heraus und wird somit in der Skizze vernachlässigt.
 Aus der Abbildung geht hervor, dass der Fußpunkt
Aus der Abbildung geht hervor, dass der Fußpunkt  des Mikrofonstativs nicht im Schatten liegt.
des Mikrofonstativs nicht im Schatten liegt.
