C2 - Stochastik

Das Postunternehmen $Q$ stellt $95\,\%$ aller Briefe am ersten Werktag nach ihrer Einlieferung zu. Für $2000$ zufällig ausgewählte Briefe, die unabhängig voneinander befördert werden, wird untersucht, ob sie am ersten Werktag nach ihrer Einlieferung zugestellt werden.

1.1

Begründe, dass die Binomialverteilung dafür geeignet ist, Vorhersagen zum Ergebnis der Untersuchung zu treffen.

(2 BE)

1.2

Bestimme unter Angabe einer geeigneten Zufallsvariablen $X$ die Wahrscheinlichkeiten der folgenden Ereignisse:

$A$ : ,,Genau $1900$ der Briefe werden am ersten Werktag nach ihrer Einlieferung zugestellt."

$B$ : ,,Mindestens $1900$ der Briefe werden am ersten Werktag nach ihrer Einlieferung zugestellt."

$C$ : ,,Mehr als $100$ der Briefe werden nicht am ersten Werktag nach ihrer Einlieferung zugestellt."

(7 BE)

1.3

Entscheide für jede der beiden Wahrscheinlichkeiten $P(B)$ und $P(C)$ aus Aufgabe 1.2, ob sie in Material 1 als dunkle Balkenfläche dargestellt wird. Begründe jeweils deine Entscheidung.

Binomialverteilung für $n=2000$ und $p=0,95$

(3 BE)

1.4

Die Zufallsvariable $Y$ sei binomialverteilt mit den Parametern $n=2000$ und $p=0,05$

die Zufallsvariable $Z$ sei binomialverteilt mit den Parametern $n=2000$ und $p=0,95.$

Entscheide für jeden der beiden Terme $I$ und $II$ , ob er die Wahrscheinlichkeit dafür angibt, dass mindestens $100$ der ausgewählten Briefe nicht am ersten Werktag nach ihrer Einlieferung zugestellt werden. Begründe jeweils deine Entscheidung.

$\begin{array}{lrll} \text{I:}\quad P(Y\leq 100) = F(2000;0,05;100) \quad \\ \text{II:}\quad P(Z\leq1900) = F(2000;0,95;1900) \quad \\ \end{array}$

(3 BE)

1.5

Berechne den Erwartungswert für die Anzahl der Briefe, die am ersten Werktag nach ihrer Einlieferung zugestellt werden.

(2 BE)

1.6

Ermittle, wie viele Briefe zufällig ausgewählt werden müssten, damit die Standardabweichung für die Anzahl der Briefe, die am ersten Werktag nach ihrer Einlieferung zugestellt werden, doppelt so groß ist wie bei $2000$ Briefen.

(3 BE)

Eine große Firma versendet einen Teil ihrer Briefe mit dem Postunternehmen $Q$ aus Aufgabe 1, den anderen Teil mit einem anderen Postunternehmen. Ein Brief der Firma wird zufällig ausgewählt und daraufhin untersucht, ob er am ersten Werktag nach seiner Einlieferung zugestellt wird (Ereignis $E$ ).
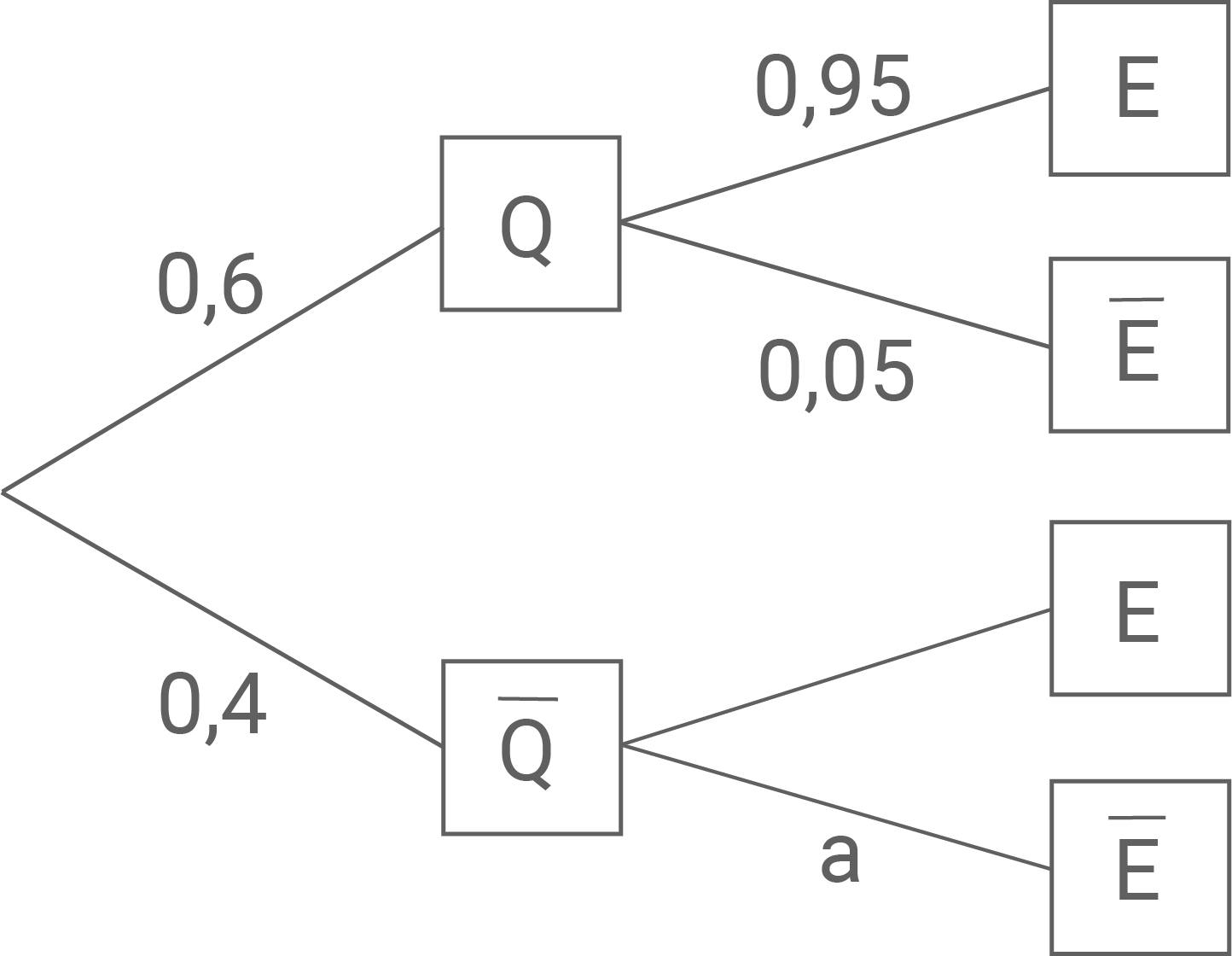
Die Abbildung in Material 2 stellt den Sachverhalt dar.

2.1

Berechne für $a=0,25$ die Wahrscheinlichkeit dafür, dass der ausgewählte Brief nicht am ersten Werktag nach seiner Einlieferung zugestellt wird.

(3 BE)

2.2

Prüfe für $a=0,25$ , ob die Ereignisse "der ausgewählte Brief wird vom Postunternehmen $Q$ befördert" und "der ausgewählte Brief wird am ersten Werktag nach seiner Einlieferung zugestellt" stochastisch unabhängig sind.

(3 BE)

2.3

Der ausgewählte Brief wird nicht am ersten Werktag nach seiner Einlieferung zugestellt. Leite einen vom Parameter $a$ abhängigen Term für die Wahrscheinlichkeit her, dass er vom Postunternehmen $Q$ befördert wurde.

(3 BE)

Das Konkurrenzunternehmen $R$ behauptet, eine bessere Zustellquote zu besitzen als das Unternehmen $Q$ aus Aufgabe 1. Diese Behauptung soll mithilfe eines Hypothesentests überprüft werden. Dabei wird für $200$ zufällig ausgewählte, von $R$ zugestellte Briefe untersucht, ob sie am ersten Werktag nach ihrer Einlieferung zugestellt werden. Bei diesem Test wird festgelegt, dass die Wahrscheinlichkeit für einen Fehler 1. Art höchstens $5 \,\%$ betragen soll.
Die kritische Zahl $k$ gibt an, wie viele der im Rahmen des Tests untersuchten Briefe mindestens am ersten Werktag nach ihrer Einlieferung zugestellt werden müssen, damit die Hypothese $H_{0}$ zugunsten von $H_{1}$ verworfen wird.

3.1

Gib die Hypothesen $H_{0}$ und $H_{1}$ für diesen Test an.

(2 BE)

3.2

Bei Unternehmen $Q$ erwartet man, dass durchschnittlich $190$ von $200$ Briefen am ersten Werktag nach ihrer Einlieferung zugestellt werden. Begründe ohne Rechnung, dass die kritische Zahl $k$ bei dem angegebenen Hypothesentest größer als $190$ sein muss.

(2 BE)

3.3

Ermittle die kritische Zahl $k$ für diesen Hypothesentest und formuliere eine Entscheidungsregel im Sachzusammenhang.

(5 BE)

3.4

Beschreibe den Fehler 1. Art im Sachzusammenhang.

(2 BE)

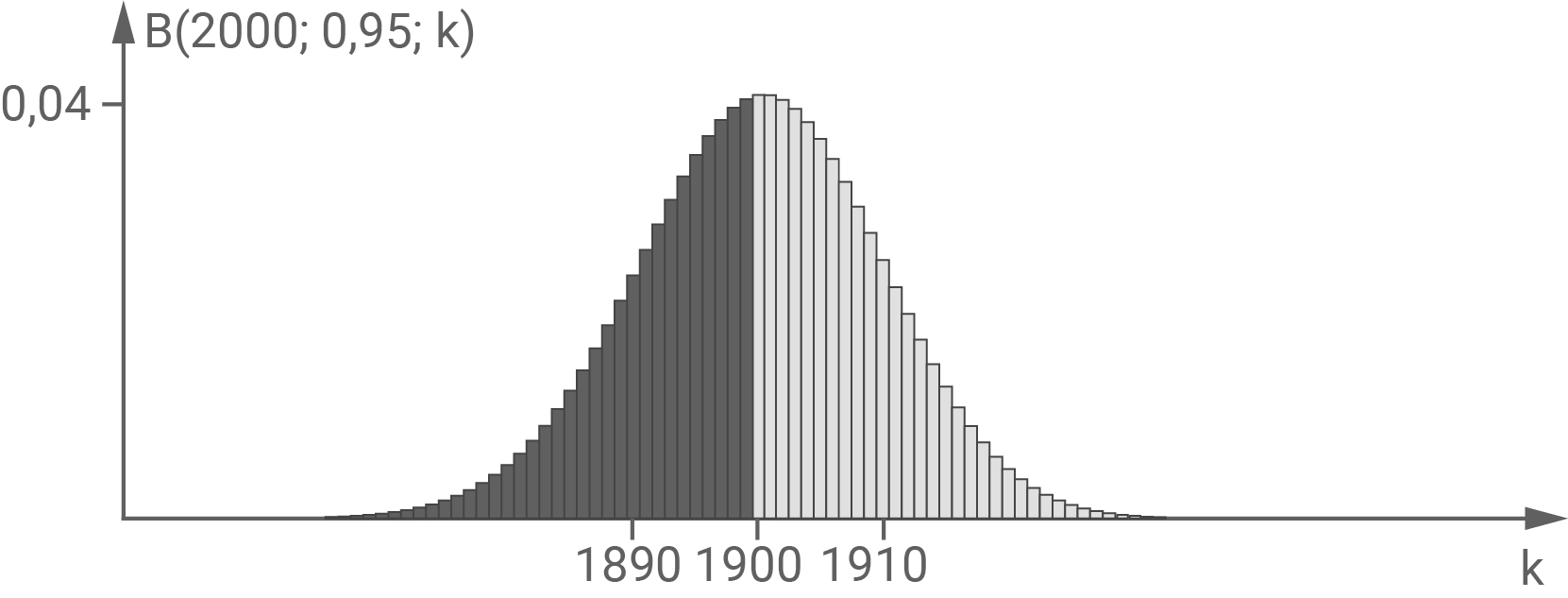
Material 1

Binomialverteilung für $n=2000$ und $p=0,95$

Material 2

1.1

Wie im Text beschrieben wird, werden die Briefe zufallig und unabhängig voneinander ausgewählt. Daher kann man den Vorgang als Bernoulli-Kette auffassen, da die Versuchsstufen unabhängig voneinander sind und die Wahrscheinlichkeit für die oben beschriebene Zustellgeschwindigkeit für jede Versuchsstufe gleich bleibt.

Somit ist die Binomialverteilung für die Untersuchung geeignet.

1.2

X: Anzahl der Briefe, die am ersten Werktag nach der Einlieferung zugestellt werden.

$P(A)$ $=P(X=1900)$ $=B(2000;0,95;1900)$ $\approx 4,09\,\%$

$P(B)$ $=P(X\geq1900)$ $=1-P(X\geq 1899)$ $=1-F(2000;0,95;1899)$ $\approx 52,7\,\%$

$P(C)$ $=P(X\leq1900)=1-P(B)$ $\approx 47,3 \,\%$

alternativ X*: Anzahl der Briefe, die am ersten Werktag nicht eingeliefert werden

$P(C)$ $=P(X^*\gt 100)$ $=1-P(X*\leq 100)$ $= 1-F(2000;0,05;100)$ $\approx 47,3 \,\%$

1.3

Die dunkel dargestellte Balkenfläche entspricht der Wahrscheinlichkeit des Ereignisses "höchstens 1899 Treffer" und damit auch der Wahrscheinlichkeit für "mehr als 100 Nicht-Treffer", also P(C).

P(B) entspricht den hellen Balkenflächen.

1.4

Term $\text {(I)}$ $P(Y\leq 100 )=F(2000;0,05;100)$ gibt die Wahrscheinlichkeit an, dass höchstens 100 Briefe nicht nach einem Tag zugestellt werden. Damit gibt dieser Term nicht die Wahrscheinlichkeit für das angegebene Ereignis an.

Term $\text{(II)}$ $P(Z\leq 1900)=F(2000;0,95,1900)$ gibt die Wahrscheinlichkeit an, dass höchstens 1900 der Briefe nach am ersten Werktag und damit mindestens 100 der Briefe nicht am ersten Werktag nach ihrer Einlieferung zugestellt werden. Daher steht Term $\text{(II)}$ für die im Text beschriebene Wahrscheinlichkeit.

1.5

Der Erwartungswert für die Anzahl an Briefen, die am ersten Werktag nach ihrer Einlieferung zugestellt werden, beträgt $E(x)= n\cdot p= 2000 \cdot 0,95 = 1900$ .

1.6

Zunächst muss die Standardabweichung für die bisher verwendete Verteilung von $X$ bestimmt werden:

$\sigma_{\text {alt }}$ $=\sqrt{ n \cdot p \cdot q}$ $=\sqrt{2000 \cdot 0,95 \cdot 0,05}$ $=\sqrt{95}$ $\approx 9,75$

Die Standardabweichung bei der neuen Anzahl von untersuchten Briefen soll doppelt so groß sein. Also muss für die Standardabweichung der neuen Untersuchung gelten:

$\sigma$ $=2 \cdot \sigma_{\text {alt }}$ $=2 \cdot \sqrt{2000 \cdot 0,95 \cdot 0,05}$ $=\sqrt{4 \cdot 2000 \cdot 0,95 \cdot 0,05}$ $=\sqrt{8000 \cdot 0,95 \cdot 0,05}$

Daher müssten 8000 Briefe untersucht werden.

2.1

Post $Q$ , anderes Postunternehmen $\overline{Q}$

$E$ ={"Zugestellte Briefe nach einem Tag"}

Hessen GK Abi 2020 Wahrscheinlichkeit Baumdiagramm

Gesucht ist für $a=0,25$ die Wahrscheinlichkeit dafür, dass der Brief nicht am ersten Werktag nach seiner Einlieferung zugestellt wird. Entlang der Pfade für das Ereignis $\overline{E}$ ergibt sich:

$P(\overline{E})= 0,6 \cdot 0,05 + 0,4 \cdot 0,25 = 0,13$

2.2

Das Ereignis $P_Q(E)=0,95$ stellt "der ausgewählte Brief wird vom Postunternehmen Q befördert" dar und $P(E)=0,6 \cdot 0,95 +0,4 \cdot 0,75 =0,87$ stellt "der ausgewählte Brief wird am ersten Werktag nach seiner Einlieferung zugestellt" dar.

Vergleichen der Ergebnisse:

$P_Q(E)=0,95 \neq 0,87=P(E)$ , d.h. die Ergebnisse sind stochastisch nicht unabhängig.

2.3

$\begin{array}[t]{rll} P_Q(E)&=& \dfrac{\overline{E} \cap Q}{\overline{E}}&\quad \scriptsize \\[5pt] P_Q(E)&=&\dfrac{0,6 \cdot 0,05}{0,6 \cdot 0,05 +0,4 \cdot a} &\quad \scriptsize \\[5pt] P_Q(E)&=& \dfrac{0,03}{0,03 + 0,4 \cdot a} &\quad \scriptsize \\[5pt] \end{array}$

3.1

Die Nullhypothese besagt, dass $R$ nicht pünktlicher ist als $Q.$

$X$ sei, wie oben festgelegt, die Anzahl der pünktlich gelieferten Briefe.

Nullhypothese $H _0: X$ ist mit $n =200$ und $p _0 \leq 0,95$ binomialverteilt.

Gegenhypothese $H _1$ : $X$ ist mit $n =200$ und $p _1\gt 0,95$ binomialverteilt.

3.2

Da R behauptet besser als Q zu sein, muss die kritische Zahl größer als der Erwartungswert für pünktlich zugestellte Briefe der Firma Q für 200 Briefe sein.

3.3

$X$ : Anzahl der Briefe, die am ersten Werktag nach der Einlieferung zugestellt werden.

$n=200$

$\begin{array}[t]{rll} P_{H_0} (X\geq k)&=& 1 - P_{H_0}(X\leq k-1) \\[5pt] &=& 1-F(200;0,95;k-1) \leq 0,05 \end{array}$

$1-F(200;0,95,194) \approx 0,062 \gt 0,05$

$1-F(200;0,95,195) \approx 0,026 \lt 0,05$

Daraus folgt, dass $k-1=195$ und somit $k=196$ ist.

Werden 196 oder mehr Briefe am ersten Werktag nach der Einlieferung zugestellt, wird die Nullhypothese verworfen und man geht davon aus, dass die Zustellquote von R mehr als 95% beträgt.

3.4

Einen Fehler 1. Art würde man begehen, wenn man aufgrund eines entsprechenden Versuchsergebnisses - also bei 196 oder mehr pünktlich gelieferten Briefen - die Nullhypothese ablehnen und daraus schließen würde, dass $R$ besser ist als $Q$ , obwohl dies in der Realität nicht so ist. $H _0$ würde also zu Unrecht verworfen.