C2.2 - Stochastik

Mehr als 200 Millionen ausrangierte Handys und Smartphones (im Folgenden als Alt-Handys bezeichnet) lagern in deutschen Wohnungen, ob als Ersatzgerät oder wegen der vielen gespeicherten Fotos.

Vor einem Einkaufszentrum werden Personen ab 16 Jahren zufällig ausgewählt und befragt, wie viele Alt-Handys sie besitzen. Es soll davon ausgegangen werden, dass die Anzahl der befragten Personen, die angeben, drei und mehr Alt-Handys, zwei Alt-Handys, ein Alt-Handy, kein Alt-Handy oder kein Handy zu besitzen, jeweils durch eine binomialverteilte Zufallsgröße beschrieben werden kann. Die im Material 1 angegebenen prozentualen Anteile sollen als Wahrscheinlichkeiten betrachtet werden.

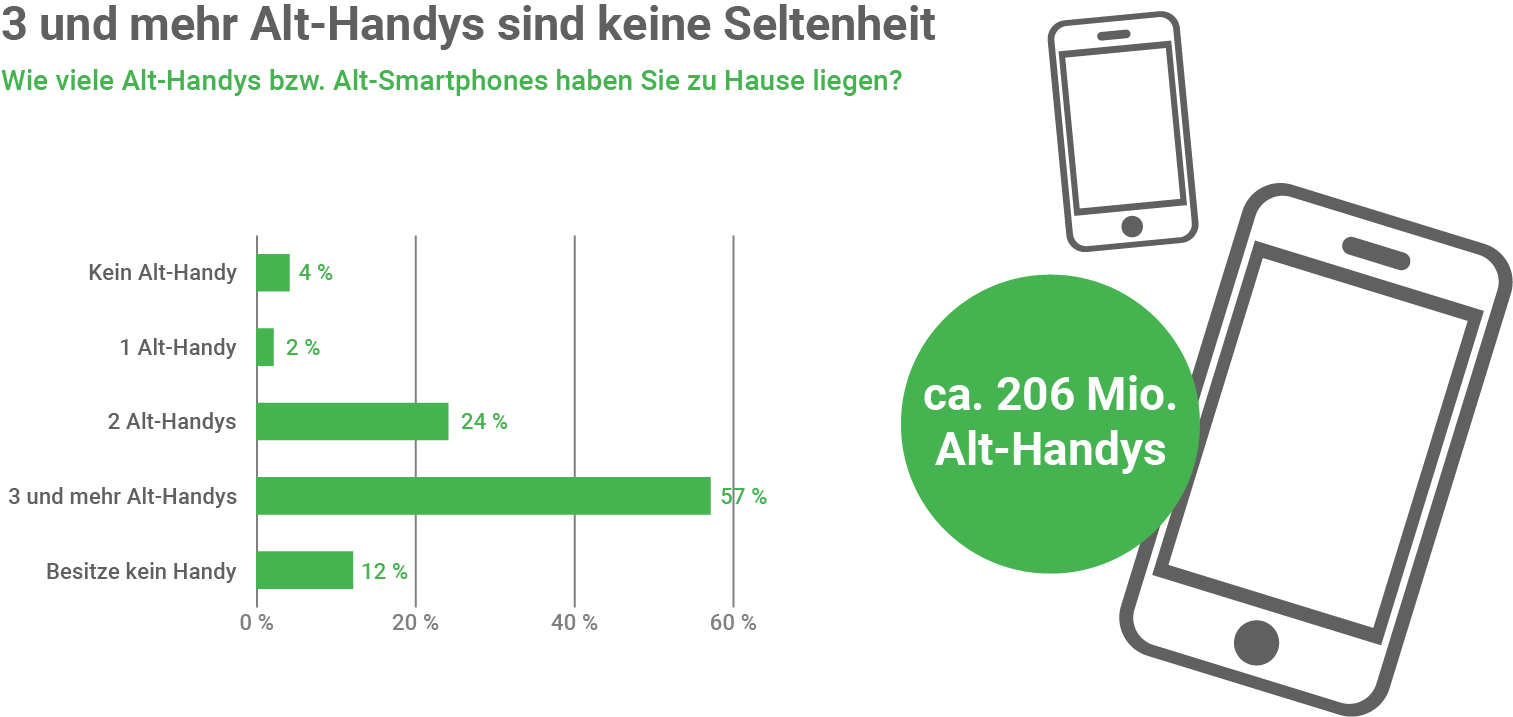
hessen mathe abi gk wtr 2022 teil c2 abbildung 1

Material 1
Hinweise: $1 \,\%$ der Befragten machte keine Angaben. Befragte, die angeben, kein Alt-Handy zu besitzen, nutzen noch ihr erstes Handy.

URL: https://www.bitkom.org/Presse/Presseinformation/Mehr-als-200-Millionen-Alt-Handys-lagern-in-deutschen-Wohnungen (abgerufen am 04.06.2021).

1.1

Es werden 80 Personen befragt. Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse.

$E_1:$

Genau 16 der befragten Personen geben an, zwei Alt-Handys zu besitzen.

$E_2:$

Höchstens 42 der befragten Personen geben an, drei und mehr Alt-Handys zu besitzen.

$E_3:$

Mindestens 3, aber höchstens 6 der befragten Personen geben an, genau ein Alt-Handy zu besitzen.

$E_4:$

Die Anzahl der befragten Personen, die angeben, kein Handy oder kein Alt-Handy zu besitzen, ist größer als die zu erwartende Anzahl.

(11 BE)

1.2

Gib den Wert des Terms $\left(\begin{array}{l}80 \\ 35\end{array}\right) \cdot 0,57^{35} \cdot 0,43^{45}$ an und erkläre die Bedeutung des Terms im Sachzusammenhang.

(3 BE)

1.3

Berechne, wie viele Personen mindestens befragt werden müssen, damit sich mit einer Wahrscheinlichkeit von mindestens $85 \,\%$ mindestens eine Person darunter befindet, die angibt, kein Alt-Handy zu besitzen.

(4 BE)

$16 \,\%$ der Deutschen ab 16 Jahren heben ihre Alt-Handys ausnahmslos auf. Für eine Studie werden 1120 Frauen ab 16 Jahren und 952 Männer derselben Altersgruppe zufällig ausgewählt und telefonisch befragt. 1612 Personen, darunter 742 Männer, geben an, dass sie ihre Alt-Handys nicht ausnahmslos aufheben.

Eine der befragten Personen wird zufällig ausgewählt und folgende Ereignisse werden betrachtet:

$W:$

„Die Person ist weiblich.“

$A:$

„Die Person gibt an, dass sie ihre Alt-Handys ausnahmslos aufhebt.“

2.1

Der Sachverhalt soll tabellarisch dargestellt werden.
Gib die fehlenden Werte in der untenstehenden Tabelle an.
Entscheide begründet, ob der prozentuale Anteil der in der Studie befragten Personen, die angeben, ihre Alt-Handys ausnahmslos aufzuheben, dem Bundesdurchschnitt entspricht.

	$\color{#fff}{A}$	$\color{#fff}{\overline{A}}$	$\color{#fff}{\sum\limits}$
$\color{#fff}{W}$
$\color{#fff}{\overline{W}}$
$\color{#fff}{\sum\limits}$

Material 2

(5 BE)

2.2

Die Terme $P_{W}(A)$ und $P( W \cap A)$ bezeichnen Wahrscheinlichkeiten.
Beschreibe die Bedeutung der Terme im Sachzusammenhang.

(2 BE)

2.3

Untersuche, ob die Wahrscheinlichkeiten $P_{\overline{A}}( W )$ und $P(W)$ übereinstimmen.
Deute dein Ergebnis im Sachzusammenhang.

(4 BE)

Eine Firma ist darauf spezialisiert, gebrauchte Smartphones, die von ihr generalüberholt, gereinigt und geprüft werden, weiter zu verkaufen. Ein Zwischenhändler bietet der Firma in einer Großlieferung gebrauchte Smartphones zu einem sehr günstigen Preis an. Erfahrungsgemäß sind $20 \,\%$ der Geräte dieses Zwischenhändlers so stark beschädigt, dass sie von der Firma nicht mehr verwertet werden können.

3.1

Ein Ankauf beim Zwischenhändler lohnt sich für die Firma nur, wenn bei einer Großlieferung im Mittel mindestens 5000 verwertbare Smartphones dabei sind.
In diesem Zusammenhang wird folgende Überlegung angestellt:

(1) $(5000+ k ) \cdot 0,2= k ( k >0)$

(2) $\ldots \Leftrightarrow k =1250$

(3) $y \geq 6250$

Erläutere den Ansatz in Zeile (1) im Sachzusammenhang. Gib in Zeile (2) die durch Auslassungspunkte gekennzeichnete fehlende Berechnung an.
Erkläre das Ergebnis in Zeile (3) im Sachzusammenhang.

(5 BE)

3.2

Die Firma überprüft zufällig ausgewählte Smartphones der Großlieferung des Zwischenhändlers. Die Zufallsgröße $Z$ beschreibe die Anzahl der verwertbaren Geräte.
Wenn $\mu$ der Erwartungswert einer binomialverteilten Zufallsgröße $Z$ ist und $\sigma$ die zugehörige Standardabweichung, dann gilt für $\sigma>3: P (\mu-2 \sigma \leq Z \leq \mu+2 \sigma) \approx 0,95$ .

3.2.1

Berechne, wie viele Geräte mindestens überprüft werden müssen, damit die Bedingung $\sigma>3$ erfüllt ist.

(2 BE)

3.2.2

Die Firma überprüft 500 Geräte. Bestimme die Wahrscheinlichkeit $P (\mu-2 \sigma \leq Z \leq \mu+2 \sigma)$ auf vier Nachkommastellen genau.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?