B1 - Analysis
Auf vielen Gebäuden befinden sich Photovoltaikanlagen. Umgangssprachlich bezeichnet man solche der Stromerzeugung dienenden Anlagen häufig als „Solaranlagen“. Die Menge des erzeugten Stroms hängt unter anderem vom Sonnenstand ab und schwankt daher im Jahres-, aber auch im Tagesverlauf.
In dieser Aufgabe wird die Leistungsabgabe einer Solaranlage auf einem Einfamilienhaus während eines sonnigen Tages im Juli 2022 näher untersucht.
Diese lässt sich in sehr guter Näherung durch die Funktion  mit
mit  modellieren.
Dabei beschreibt
modellieren.
Dabei beschreibt  die Zeit in Stunden nach Tagesbeginn um Mitternacht und
die Zeit in Stunden nach Tagesbeginn um Mitternacht und  die Leistungsabgabe in
die Leistungsabgabe in  (Kilowatt). Der Definitionsbereich der Funktion
(Kilowatt). Der Definitionsbereich der Funktion  ist
ist 
1
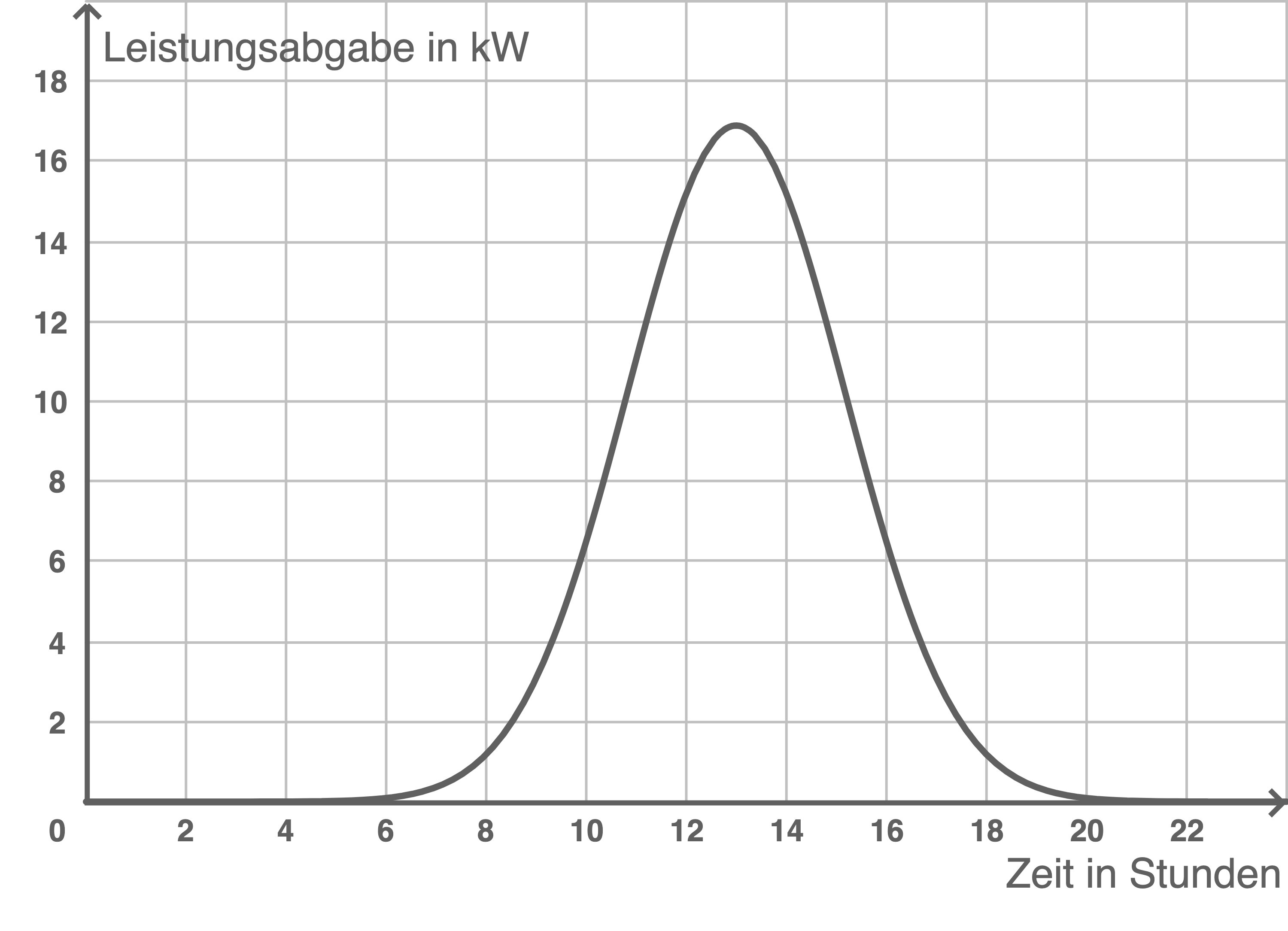
Der Graph der Funktion  ist in Abbildung 1 dargestellt.
Beschreibe den Verlauf des Graphen im Sachzusammenhang unter Bezugnahme auf wesentliche Eigenschaften und charakteristische Punkte.
ist in Abbildung 1 dargestellt.
Beschreibe den Verlauf des Graphen im Sachzusammenhang unter Bezugnahme auf wesentliche Eigenschaften und charakteristische Punkte.

Abbildung 1
(5 BE)
2
Im Zeitraum von 9 Uhr bis 17 Uhr, d. h. für  , sollen anstelle der Funktion
, sollen anstelle der Funktion  vereinfachend ganzrationale Funktionen zur Modellierung der Leistungsabgabe der Solaranlage verwendet werden.
Als erste stark vereinfachende Alternative wird die Funktion
vereinfachend ganzrationale Funktionen zur Modellierung der Leistungsabgabe der Solaranlage verwendet werden.
Als erste stark vereinfachende Alternative wird die Funktion  mit der Funktionsgleichung
mit der Funktionsgleichung  verwendet. Der Graph der Funktion
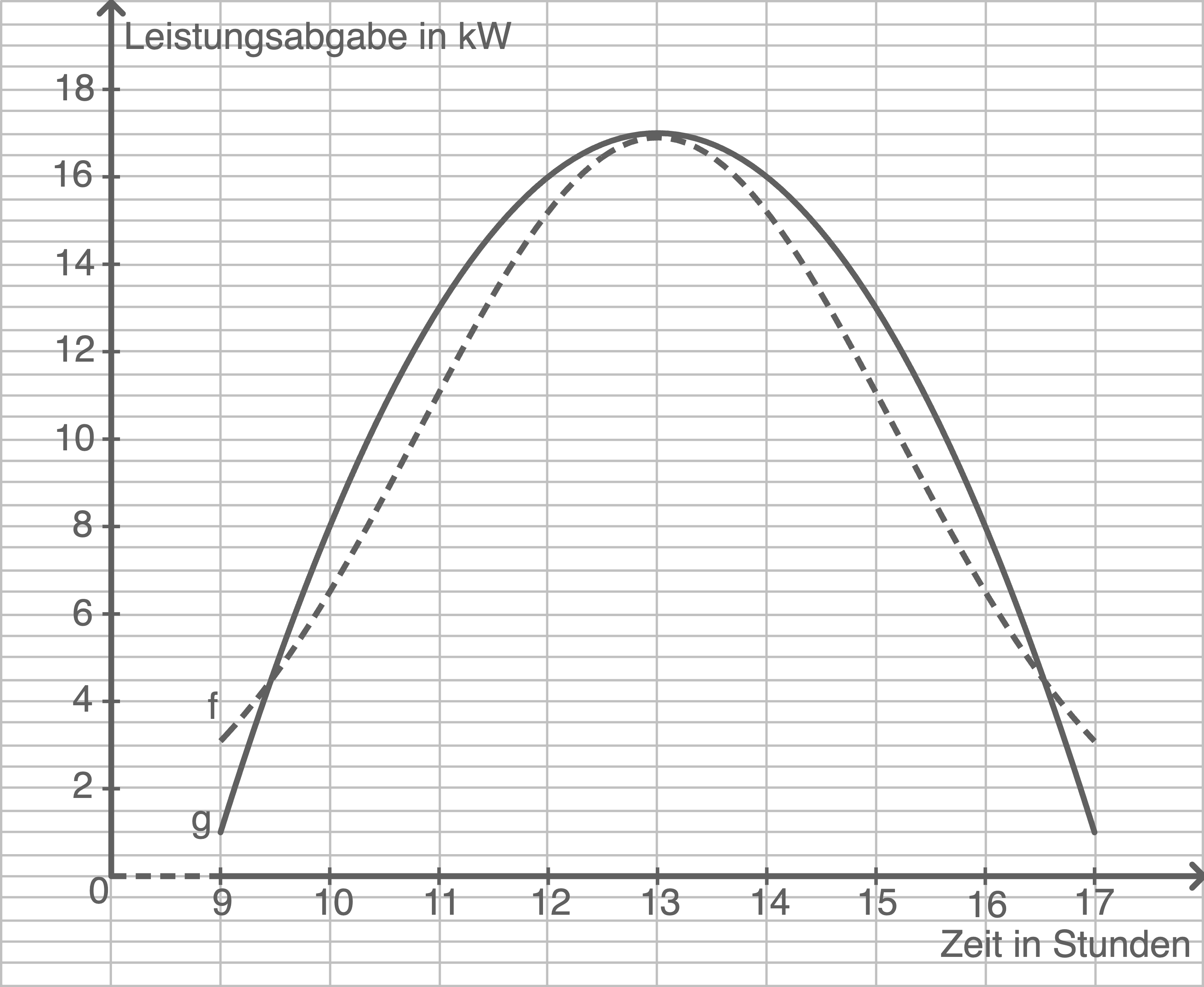
verwendet. Der Graph der Funktion  ist in Abbildung 2 im nun betrachteten Intervall zusammen mit dem Graphen von
ist in Abbildung 2 im nun betrachteten Intervall zusammen mit dem Graphen von  dargestellt.
Als zweite Alternative werden ganzrationale Funktionen der Funktionenschar
dargestellt.
Als zweite Alternative werden ganzrationale Funktionen der Funktionenschar  mit
mit  verwendet.
Für beide Alternativen gibt
verwendet.
Für beide Alternativen gibt  jeweils die Zeit in Stunden nach Mitternacht an, die Funktionswerte geben jeweils die Leistungsabgabe in
jeweils die Zeit in Stunden nach Mitternacht an, die Funktionswerte geben jeweils die Leistungsabgabe in  an.
an.

Abbildung 2
2.1.1
Der Graph der Funktion  besitzt zwei Wendepunkte.
Erläutere, warum unter Berücksichtigung dieser Wendepunkte eine alternative ganzrationale Modellfunktion mindestens vierten Grades sein muss.
besitzt zwei Wendepunkte.
Erläutere, warum unter Berücksichtigung dieser Wendepunkte eine alternative ganzrationale Modellfunktion mindestens vierten Grades sein muss.
(2 BE)
2.1.2
Erläutere anhand der Funktionsgleichung, welche Symmetrieeigenschaft die Graphen der zur Funktionenschar  gehörigen Funktionen aufweisen.
gehörigen Funktionen aufweisen.
(2 BE)
2.2
Bestimme diejenige Funktion  der Schar
der Schar  , deren Graph durch
, deren Graph durch  verläuft und den Wendepunkt
verläuft und den Wendepunkt  besitzt.
Zeichne den Graphen der Funktion
besitzt.
Zeichne den Graphen der Funktion  in die Abbildung 2.
Entscheide anschließend begründet anhand von Abbildung 2, welche der beiden Alternativen besser zur Modellierung der Funktion
in die Abbildung 2.
Entscheide anschließend begründet anhand von Abbildung 2, welche der beiden Alternativen besser zur Modellierung der Funktion  geeignet ist.
geeignet ist.
(7 BE)
2.3
Die in der Zeitspanne von  bis
bis  bereitgestellte Energiemenge berechnet man, indem man die betrachtete Modellfunktion über dem Zeitintervall
bereitgestellte Energiemenge berechnet man, indem man die betrachtete Modellfunktion über dem Zeitintervall ![\(\left[t_1 ; t_2\right]\)](https://mathjax.schullv.de/d18b1aa5839b36a46174fb5c562cffbf7f4540825a7337a5ea81aad290551dda?color=5a5a5a) integriert.
Berechne die von 10 Uhr bis 16 Uhr gemäß der Modellierung mit der Funktion
integriert.
Berechne die von 10 Uhr bis 16 Uhr gemäß der Modellierung mit der Funktion  bereitgestellte Energiemenge in Kilowattstunden
bereitgestellte Energiemenge in Kilowattstunden 
(5 BE)
3
Betrachtet wird nun wieder die Funktion  die im Vergleich zu den Funktionen
die im Vergleich zu den Funktionen  und
und  die Leistungsabgabe im Verlauf des Tages deutlich präziser beschreibt.
die Leistungsabgabe im Verlauf des Tages deutlich präziser beschreibt.
3.1
Der Inhalt der Fläche, die der Graph der Funktion  in einem Intervall mit der
in einem Intervall mit der  -Achse einschließt, kann nicht algebraisch mit Hilfe der Integralrechnung berechnet werden.
Um die von 10 Uhr bis 16 Uhr bereitgestellte Energiemenge näherungsweise zu ermitteln, soll daher der Inhalt der zugehörigen Fläche mit Hilfe einer Rechtecksumme approximiert werden.
Skizziere in der Abbildung 1 die zur Untersumme zugehörige Fläche, die man bei Unterteilung des Intervalls
-Achse einschließt, kann nicht algebraisch mit Hilfe der Integralrechnung berechnet werden.
Um die von 10 Uhr bis 16 Uhr bereitgestellte Energiemenge näherungsweise zu ermitteln, soll daher der Inhalt der zugehörigen Fläche mit Hilfe einer Rechtecksumme approximiert werden.
Skizziere in der Abbildung 1 die zur Untersumme zugehörige Fläche, die man bei Unterteilung des Intervalls ![\([10 ; 16]\)](https://mathjax.schullv.de/e401cf2b79cd99f1c677e252c0558ff7e51477cfa48e1840f3a3079f68218d63?color=5a5a5a) in drei Abschnitte gleicher Breite erhält.
Berechne den Wert dieser Untersumme.
in drei Abschnitte gleicher Breite erhält.
Berechne den Wert dieser Untersumme.
(7 BE)
3.2
Nimm ohne Verwendung einer Rechnung Stellung zu der Aussage:
„Die Rechtecksumme, durch die in Aufgabe 3.1 die von 10 Uhr bis 16 Uhr bereitgestellte Energiemenge näherungsweise ermittelt wird, ist sicher kleiner als die gemäß der Modellierung mit der Funktion  bereitgestellte Energiemenge in dieser Zeitspanne.“
bereitgestellte Energiemenge in dieser Zeitspanne.“
(2 BE)
3.3
Gib den Wert des Terms  an.
Dieser Wert weicht deutlich von dem mit Hilfe der Untersumme in Aufgabe 3.1 bestimmten Wert ab.
Gib zwei verschiedene Möglichkeiten an, wie man die in Aufgabe 3.1 vorgenommene Approximation verbessern könnte.
an.
Dieser Wert weicht deutlich von dem mit Hilfe der Untersumme in Aufgabe 3.1 bestimmten Wert ab.
Gib zwei verschiedene Möglichkeiten an, wie man die in Aufgabe 3.1 vorgenommene Approximation verbessern könnte.
(4 BE)
4
Die Hauseigentümer besitzen ein Elektroauto und eine Ladestation. Diese bezieht so viel Strom wie möglich direkt von der Solaranlage auf dem eigenen Hausdach.
Zum Laden des Elektroautos wird eine konstante Ladeleistung von  benötigt. Fällt die Leistungsabgabe der Solaranlage unter diesen Wert, so wird der zusätzlich benötigte Strom zum Preis von
benötigt. Fällt die Leistungsabgabe der Solaranlage unter diesen Wert, so wird der zusätzlich benötigte Strom zum Preis von  pro
pro  aus dem öffentlichen Stromnetz hinzugefügt.
Vereinfachend kann davon ausgegangen werden, dass über den Ladevorgang hinaus im betrachteten Zeitraum kein Strom benötigt wird.
Die Hauseigentümer schließen ihr Elektroauto um 14 Uhr an die Ladestation an und wollen
aus dem öffentlichen Stromnetz hinzugefügt.
Vereinfachend kann davon ausgegangen werden, dass über den Ladevorgang hinaus im betrachteten Zeitraum kein Strom benötigt wird.
Die Hauseigentümer schließen ihr Elektroauto um 14 Uhr an die Ladestation an und wollen  aufladen. Demnach bleibt das Elektroauto für drei Stunden angeschlossen.
Zur Modellierung der Leistungsabgabe der Solaranlage wird im Folgenden die Funktion
aufladen. Demnach bleibt das Elektroauto für drei Stunden angeschlossen.
Zur Modellierung der Leistungsabgabe der Solaranlage wird im Folgenden die Funktion  verwendet.
Erläutere den Ansatz in Zeile
verwendet.
Erläutere den Ansatz in Zeile  sowie die Berechnung in Zeile
sowie die Berechnung in Zeile  im Sachzusammenhang.
Deute die Rechnung und das Ergebnis in Zeile
im Sachzusammenhang.
Deute die Rechnung und das Ergebnis in Zeile  im Sachzusammenhang.
im Sachzusammenhang.
(6 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
Der Graph der Funktion  zeigt den Verlauf der Leistungsabgabe über einen Zeitraum von 24 Stunden, was einem kompletten Tag entspricht. Die Zeit
zeigt den Verlauf der Leistungsabgabe über einen Zeitraum von 24 Stunden, was einem kompletten Tag entspricht. Die Zeit  auf der
auf der  -Achse reicht von 0 bis 24 Stunden, wobei 0 Uhr Mitternacht und 24 Uhr Mitternacht des nächsten Tages entspricht.
Der Graph erreicht seinen höchsten Punkt bei ungefähr
-Achse reicht von 0 bis 24 Stunden, wobei 0 Uhr Mitternacht und 24 Uhr Mitternacht des nächsten Tages entspricht.
Der Graph erreicht seinen höchsten Punkt bei ungefähr  da die Solaranlage um etwa 13 Uhr, wenn die Sonne am höchsten am Himmel steht, die maximale Leistung erzeugt.
Die Leistungsabgabe am Anfang und Ende des Tages ist niedrig, weil die Sonne niedriger am Himmel steht oder aufgeht bzw. untergeht.
Der Graph ist annähernd symmetrisch um
da die Solaranlage um etwa 13 Uhr, wenn die Sonne am höchsten am Himmel steht, die maximale Leistung erzeugt.
Die Leistungsabgabe am Anfang und Ende des Tages ist niedrig, weil die Sonne niedriger am Himmel steht oder aufgeht bzw. untergeht.
Der Graph ist annähernd symmetrisch um  Das bedeutet, dass die Leistungsabgabe morgens und abends ähnlich ist, da die Sonnenintensität zu diesen Zeiten vergleichbar ist.
Das bedeutet, dass die Leistungsabgabe morgens und abends ähnlich ist, da die Sonnenintensität zu diesen Zeiten vergleichbar ist.
2.1.1
Die notwendige Bedingung für Wendestellen ist gegeben durch  Da der Graph von
Da der Graph von  genau zwei Wendepunkte besitzt, gibt es für die Gleichung
genau zwei Wendepunkte besitzt, gibt es für die Gleichung  folglich zwei Lösungen. Die Funktion von
folglich zwei Lösungen. Die Funktion von  muss somit mindestens zweiten Grades sein.
Beim Ableiten einer Funktion geht jeweils ein Grad verloren. Hat die Funktion
muss somit mindestens zweiten Grades sein.
Beim Ableiten einer Funktion geht jeweils ein Grad verloren. Hat die Funktion  mindestens den Grad zwei, so muss die Funktion
mindestens den Grad zwei, so muss die Funktion  folglich mindestens vierten Grades sein.
folglich mindestens vierten Grades sein.
2.1.2
Da der Funktionsterm von  ganzrational ist und ausschließlich Potenzen von
ganzrational ist und ausschließlich Potenzen von  mit geradzahligen Exponenten enthält, ist der Graph von
mit geradzahligen Exponenten enthält, ist der Graph von  achsensymmetrisch bezüglich der Geraden, die durch Verschiebung der
achsensymmetrisch bezüglich der Geraden, die durch Verschiebung der  -Achse um
-Achse um  in
in  -Richtung erhalten wird. Somit ist der Graph von
-Richtung erhalten wird. Somit ist der Graph von  symmetrisch zur Geraden mit der Gleichung
symmetrisch zur Geraden mit der Gleichung 
2.2
Funktion bestimmen
Da der Graph durch den Punkt  verlaufen soll, gilt:
verlaufen soll, gilt:
 Zudem soll der Graph den Wendepunkt
Zudem soll der Graph den Wendepunkt  besitzen. Mit der notwendigen Bedingung für Wendestellen ergeben sich damit also die beiden folgenden Bedingungen:
besitzen. Mit der notwendigen Bedingung für Wendestellen ergeben sich damit also die beiden folgenden Bedingungen:

 Insgesamt soll also folgendes Gleichungssystem erfüllt werden:
Insgesamt soll also folgendes Gleichungssystem erfüllt werden:
 Mit dem CAS ergeben sich:
Mit dem CAS ergeben sich:


 Die gesuchte Funktion von
Die gesuchte Funktion von  ist somit gegeben durch
ist somit gegeben durch  Graphen zeichnen
Graphen zeichnen
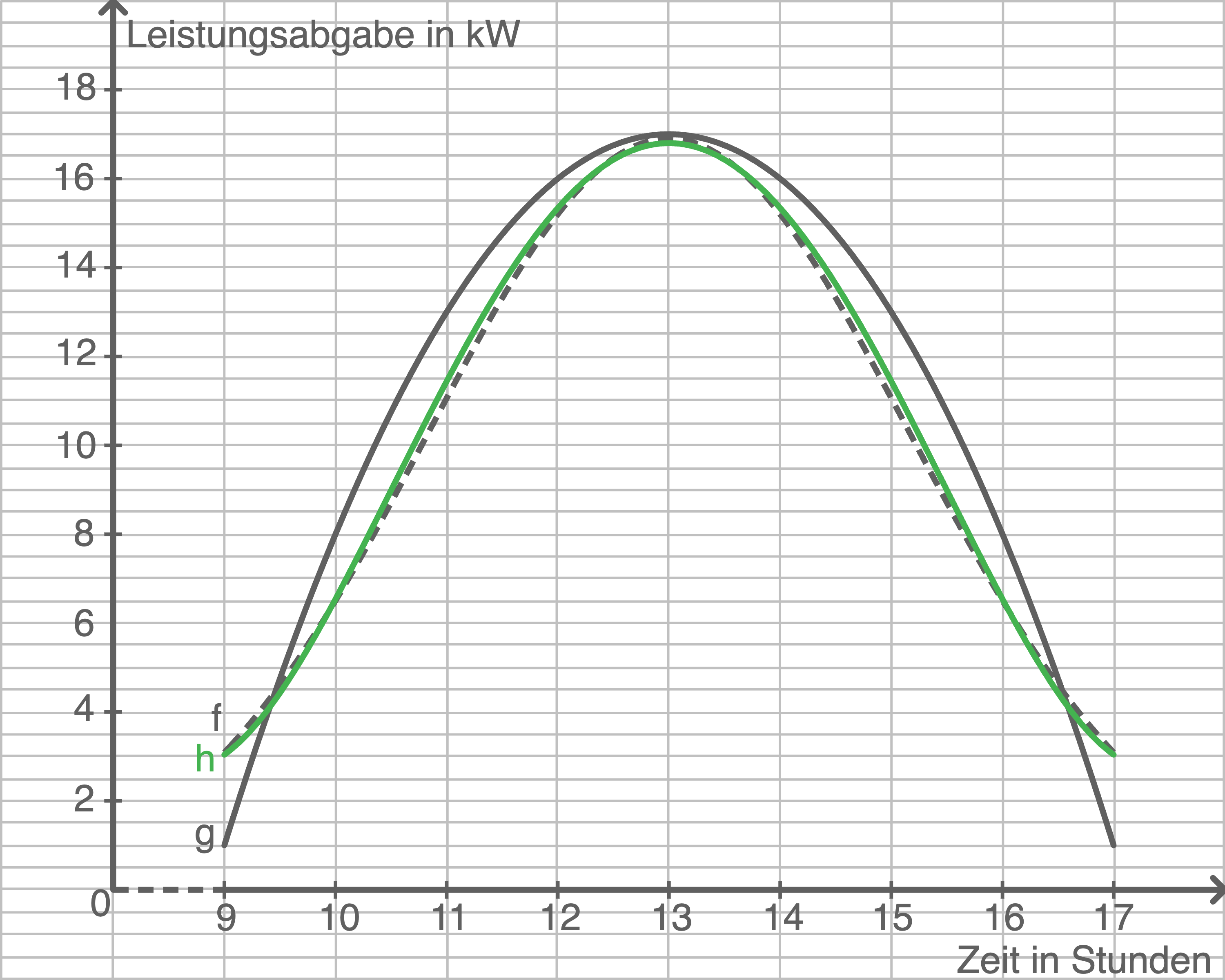 Entscheidung
Die Abbildung 2 zeigt, dass sich der Graph von
Entscheidung
Die Abbildung 2 zeigt, dass sich der Graph von  deutlich stärker dem Graphen von
deutlich stärker dem Graphen von  annähert als der Graph von
annähert als der Graph von  Somit ist die Funktion
Somit ist die Funktion  die bessere Alternative zur Modellierung der Funktion
die bessere Alternative zur Modellierung der Funktion 

2.3
3.1
Untersumme skizzieren
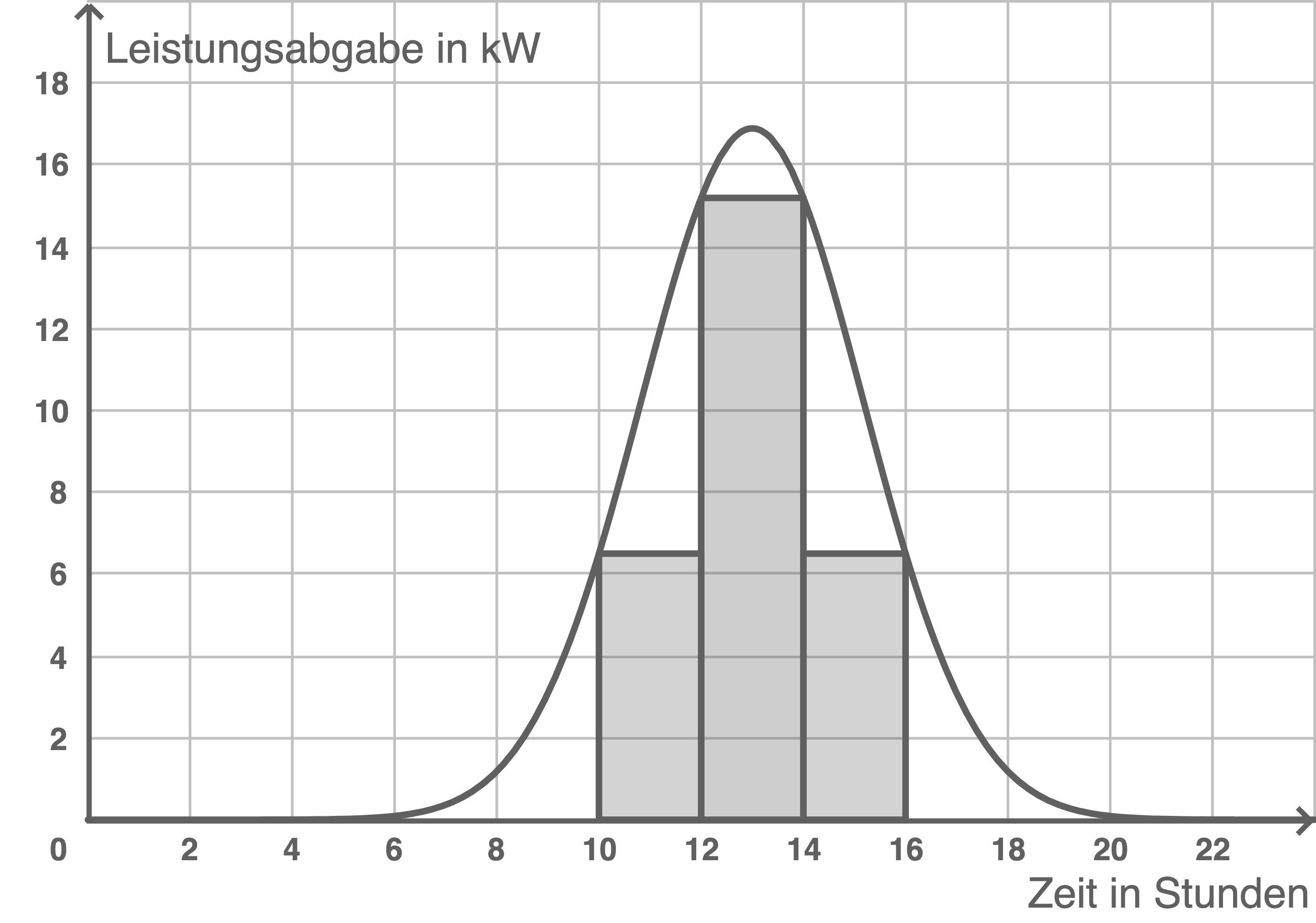 Wert berechnen
Wegen
Wert berechnen
Wegen  folgt, dass auch die Flächen des ersten und des dritten Abschnitts gleich groß sind.
Für diese gilt:
folgt, dass auch die Flächen des ersten und des dritten Abschnitts gleich groß sind.
Für diese gilt:
![\(A_{1/3}= 2\cdot 6,5= 13 \left[\,\text{kWh}\right]\)](https://mathjax.schullv.de/76489d793eb57ffd99a0baac197d8c89630fc9f8406127200380922c4657b90b?color=5a5a5a) Die Fläche des zweiten Abschnitts ergibt sich analog mit:
Die Fläche des zweiten Abschnitts ergibt sich analog mit:
![\(A_2=2\cdot 15,2=30,4 \left[\,\text{kWh}\right] \)](https://mathjax.schullv.de/5d01a471da6d59d08a13dce795f81cdbc18162083ce778e142c7e49596504846?color=5a5a5a) Der Wert der Untersumme ist somit gegeben durch:
Der Wert der Untersumme ist somit gegeben durch:
![\(\begin{array}[t]{rll}
U&=& A_1+A_2+A_3 & \\[5pt]
&=& 13+30,4+13 & \\[5pt]
&=& 56,4 \left[\,\text{kWh}\right]
\end{array}\)](https://mathjax.schullv.de/2123354396b21cf9251e4ff8fbeb71021226291373fa6a9d0f801230f7cc2abc?color=5a5a5a)

3.2
Die Rechtecksumme, die die von 10 Uhr bis 16 Uhr bereitgestellte Energie näherungsweise ermittelt, ist eine Untersumme und approximiert die Fläche unter der tatsächlichen Energiekurve durch Rechtecke.
Die Rechtecke der Untersumme haben den kleinsten Funktionswert  im jeweiligen Teilintervall als Höhe. Daher ist der Flächeninhalt aller Rechtecke der Untersumme insgesamt sicher kleiner als die Fläche
im jeweiligen Teilintervall als Höhe. Daher ist der Flächeninhalt aller Rechtecke der Untersumme insgesamt sicher kleiner als die Fläche  Die Aussage ist somit korrekt.
Die Aussage ist somit korrekt.
3.3
Wert angeben
Mit dem CAS ergibt sich:
 Verbesserungsmöglichkeiten angeben
Umso kleiner die Abschnitte sind, desto besser nähert sich die Approximation der tatsächlichen Kurve an. Eine Möglichkeit zur Verbesserung wäre somit die Unterteilung des Intervalls in kürzere und dementsprechend mehr Abschnitte.
Eine weitere Verbesserungsmöglichkeit wäre die Wahl des Durchschittsfunktionswertes anstatt des kleinsten Funktionswertes der jeweiligen Abschnitte als Höhe.
Verbesserungsmöglichkeiten angeben
Umso kleiner die Abschnitte sind, desto besser nähert sich die Approximation der tatsächlichen Kurve an. Eine Möglichkeit zur Verbesserung wäre somit die Unterteilung des Intervalls in kürzere und dementsprechend mehr Abschnitte.
Eine weitere Verbesserungsmöglichkeit wäre die Wahl des Durchschittsfunktionswertes anstatt des kleinsten Funktionswertes der jeweiligen Abschnitte als Höhe.
4
Zeile (1)
Im ersten Schritt werden die Zeitpunkte berechnet, zu denen die Leistungsabgabe der Solaranlage  beträgt.
Aufgrund des Verlauf des Graphen von
beträgt.
Aufgrund des Verlauf des Graphen von  lässt sich also schließen, dass zwischen 11 Uhr und 15 Uhr eine konstante Ladeleistung von mindestens
lässt sich also schließen, dass zwischen 11 Uhr und 15 Uhr eine konstante Ladeleistung von mindestens  gegeben ist.
In diesem Zeitraum ist somit genügend Solarstrom für die Ladestation verfügbar.
Zeile (2)
Im zweiten Schritt wird der verfügbare Solarstrom während den drei Stunden, in welchen das Elektroauto an die Ladestation angeschlossen ist, berechnet.
Aus dem Ansatz aus Zeile
gegeben ist.
In diesem Zeitraum ist somit genügend Solarstrom für die Ladestation verfügbar.
Zeile (2)
Im zweiten Schritt wird der verfügbare Solarstrom während den drei Stunden, in welchen das Elektroauto an die Ladestation angeschlossen ist, berechnet.
Aus dem Ansatz aus Zeile  folgt, dass die Leistungsabgabe der Solaranlage in der ersten Stunde zwischen 14 Uhr und 15 Uhr ausreichend ist. Für eine Stunde werden somit die benötigten
folgt, dass die Leistungsabgabe der Solaranlage in der ersten Stunde zwischen 14 Uhr und 15 Uhr ausreichend ist. Für eine Stunde werden somit die benötigten  bereitgestellt.
Das Integral repräsentiert die Energiemenge, die in den folgenden zwei Stunden von der Solaranlage erzeugt wird.
Zeile (3)
In dieser Zeile wird der Gesamtstrombedarf für das Laden des Elektroautos berechnet. Es sollen insgesamt
bereitgestellt.
Das Integral repräsentiert die Energiemenge, die in den folgenden zwei Stunden von der Solaranlage erzeugt wird.
Zeile (3)
In dieser Zeile wird der Gesamtstrombedarf für das Laden des Elektroautos berechnet. Es sollen insgesamt  geladen werden.
Die bereits durch die Solaranlage und die konstante Ladeleistung gedeckte Energiemenge von
geladen werden.
Die bereits durch die Solaranlage und die konstante Ladeleistung gedeckte Energiemenge von  wird von den
wird von den  abgezogen, um den noch benötigten Strom zu erhalten.
Da dieser zusätzliche Strom aus dem öffentlichen Netz bezogen wird und
abgezogen, um den noch benötigten Strom zu erhalten.
Da dieser zusätzliche Strom aus dem öffentlichen Netz bezogen wird und  pro
pro  kostet, ergeben sich für die Gesamtkosten des zusätzlichen Stroms somit
kostet, ergeben sich für die Gesamtkosten des zusätzlichen Stroms somit 