A2 - Analysis

Die Energie der Sonnenstrahlung kann mittels Photovoltaik in elektrische Energie umgewandelt werden. Das hessische statistische Landesamt hat im Februar 2017 folgende Werte für die im jeweiligen Jahr insgesamt auf diesem Weg in Hessen erzeugte elektrische Energie veröffentlicht.

Jahr	Energie in Mio. $\color{#fff}{\text{kWh}}$ im Jahr
$1995$	$0,1$
$2000$	$0,7$
$2003$	$19,6$
$2005$	$64,1$
$2009$	$352,9$
$2010$	$614,3$
$2011$	$973,5$
$2012$	$1.261,6$
$2013$	$1.393,8$
$2014$	$1.520,3$
$2015$	$1.631,3$

Hessisches Statistisches Landesamt (Hrsg.): Energieversorgung in Hessen im November 2016 (2017),
URL: https://statistik.hessen.de/sites/
statistik.hessen.de/files/EIV1_EIV2_EIV3m_16-11.pdf (abgerufen am 03.09.2017).

Die Entwicklung der im Zeitraum von Beginn des Jahres 1995 bis einschließlich 2015 in Hessen durch Photovoltaik erzeugten elektrischen Energie soll mathematisch modelliert werden.

Im Material sind die Tabellenwerte in einem Säulendiagramm dargestellt. Das Jahr 2000 wird als Zeitpunkt $t = 0$ betrachtet. Bestimmt man mit einem gängigen Verfahren eine Trendlinie für die Tabellenwerte im Intervall $[-5; 10],$ so erhält man eine Funktion $f_1$ mit

$f_1(t) = 1,7627 \cdot \mathrm e^{0,6074 \cdot t} ,- 5 \leq t \leq 10 .$

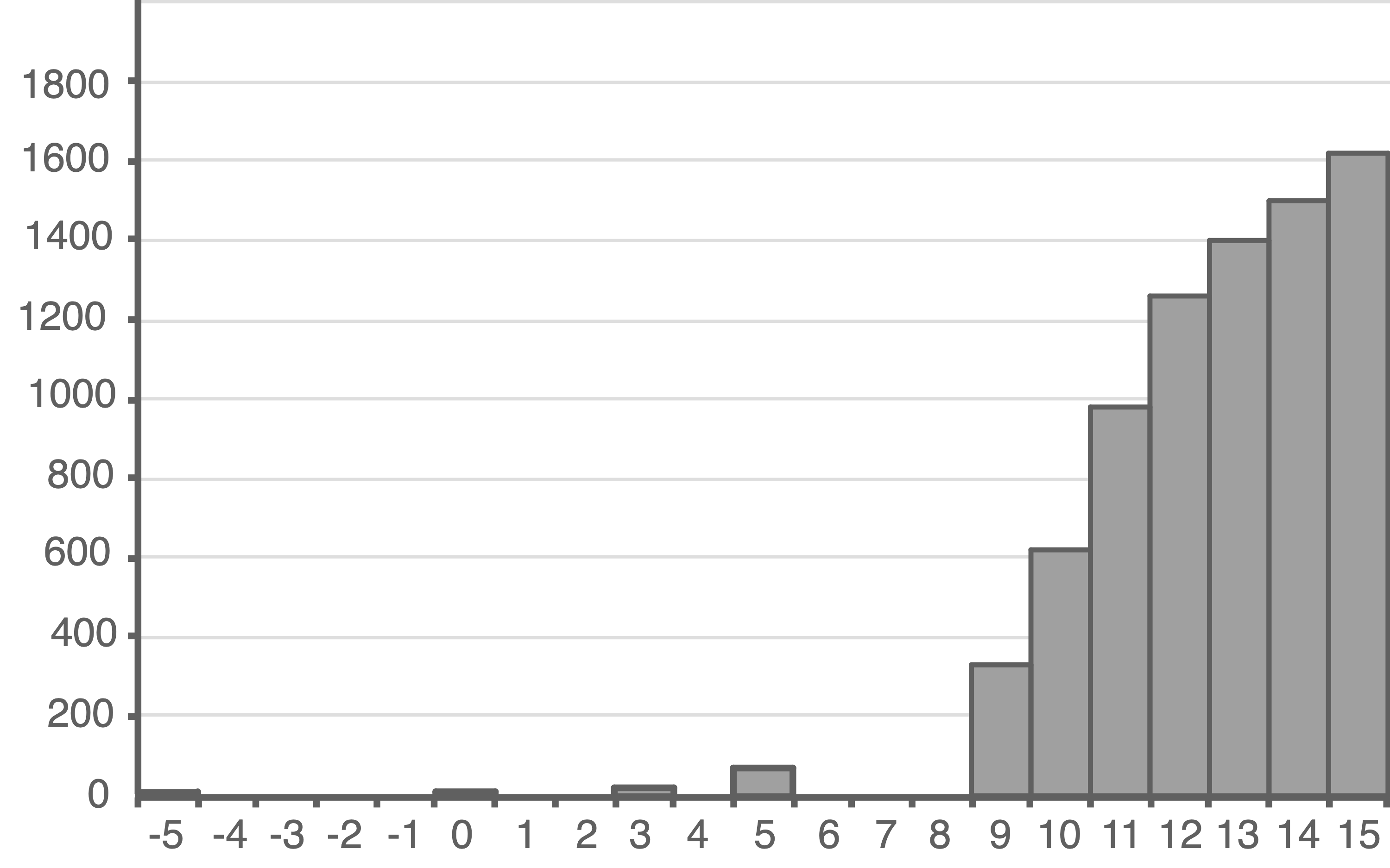
Die Höhe der Säule gibt im jeweiligen Jahr $t$ (wobei $t=0$ dem Jahr 2000 entspricht) insgesamt mittels Photovoltaik in Hessen erzeugte elektrische Energie an. Für die nicht dargestellten Jahre liegen keine Werte vor.

Säulendiagramm: Stromerzeugung aus Photovoltaik in Hessen 1995, 2000, 2003, 2005 und 2009 bis 2015

1.1

Bestimme für diese Funktion den Wert des Terms

Term anzeigen

und erläutere dessen Bedeutung.

(5 BE)

1.2

Verwendet man ein anderes Verfahren zur Bestimmung der Trendlinie, so erhält man die Funktion

$f_2$ mit $f_2(t)= 3,615\cdot \mathrm e^{0,513\cdot t},$ $-5\leq t\leq 10,$ sowie für den Ausdruck $\Delta$ aus Aufgabe 1.1 den Wert $\Delta \approx 81.$

Beurteile, welche der beiden Funktionen $f_1$ und $f_2$ besser geeignet ist, um anhand der Tabellenwerte die Entwicklung der im fraglichen Zeitraum in Hessen durch Photovoltaik erzeugten elektrischen Energie zu modellieren.

(3 BE)

1.3

Für $t \in [10;15]$ wurde durch Regression die Funktion $g$ mit

$g(t) = 1.739,698 - 1.128,845 \cdot \mathrm e^{- 0,407 \cdot ( t - 10)}$

ermittelt.
Begründe, dass die Graphen der Funktionen $f_2$ und $g$ an der Stelle $t = 10$ gut aneinander passen, und nimm unter Einbezug geeigneter Winkel Stellung zu der Aussage: „Sie gehen knickfrei ineinander über.“

(8 BE)

Mit einem anderen Ansatz zur Modellierung erhält man die Funktion $h$ mit $h(t)= \dfrac{A}{1 + B \cdot \mathrm e^{- k \cdot t}}$ und $A = 1.643,35,$ $B = 4.840,21,$ $k = 0,8.$

2.1

Gib einen Schätzwert für die im Jahr 2020 in Hessen mittels Photovoltaik erzeugte elektrische Energie anhand dieses Modells an.

(2 BE)

2.2

Begründe, dass der Grenzwert der Funktion $h$ für $t \to \infty \; 1.643,35$ beträgt.

(4 BE)

2.3

Bestimme den Wert des größten Wachstums von $h$ und deute ihn im Sachzusammenhang.

(7 BE)

3.1

Erläutere die untenstehende Rechnung sowie die mathematische Bedeutung des Wertes $\overline{E}.$

Rechnung anzeigen

(7 BE)

3.2

Ermittle mithilfe der Funktion $h$ die von Beginn des Jahres 1995 bis einschließlich 2015 in Hessen durchschnittlich pro Jahr durch Photovoltaik erzeugte elektrische Energie.

(4 BE)

1.1

Definition der Funktion $f_1$ in dem CAS und anschließende Berechnung des Terms liefert:

Rechenweg anzeigen

$\Delta \approx 4648,08$

Der Term gibt die mittlere quadratische Abweichung der tatsächlichen Werte des zwischen 1995 und 2010 in Hessen durch Photovoltaik erzeugten Stroms von der Modellierung dieser Werte durch die Funktion $f_1$ an. Der Wert beläuft sich auf ca. $4648$ Millionen $\text{kWh}.$

1.2

Je kleiner der Wert $\Delta$ ist, desto näher liegt die Modellfunktion an den tatsächlichen Werten.
Die Funktion $f_2$ ist damit besser zur Modellierung geeignet als die Funktion $f_1.$

1.3

1. Schritt: Funktionswerte bestimmen

Rechenweg anzeigen

\begin{array}[t]{rll} f_2(10)&\approx& 611,0 \\[10pt] g(10)&=& 610,9 \\[5pt] \end{array} 

An der Übergangsstelle $t=10$ nehmen beide Funktionen mit $611,0$ und $610,9$ in etwa identische Werte an, ihre Graphen gehen somit nahezu ohne Sprung ineinander über.

2. Schritt: Steigungswerte bestimmen

Die Ableitungen der Funktionen werden mit dem CAS bestimmt:

TI nspire CAS:

menu $\to$ 4: Analysis $\to$ 1: Ableitung

Casio Classpad II:

keyboard $\to$ Math2 $\to 

\frac{d}{d \Box}\Box$

Einsetzen von $t=10$ liefert:

$\(\begin{array}[t]{rll} f_2$

Einsetzen in die Formel für den Schnittwinkel liefert:

Rechenweg anzeigen

$\alpha \approx -0,06^{\circ}$

Die Graphen schneiden sich unter einem Winkel der Größe $0,06^{\circ},$ sie gehen also nahezu knickfrei ineinander über. Insgesamt passen die beiden Graphen von $f_2$ und $g$ an der Stelle $t=10$ somit gut aneinander.

2.1

Einsetzen von $t=20$ liefert:

Rechenweg anzeigen

$h(20)\approx 1642,46$

Aus der Modellierung mit der Funktion $h$ ergibt sich für die im Jahr 2020 in Hessen mittels Photovoltaik erzeugte elektrische Energie ein Schätzwert von ca. $1642,46$ Millionen $\text{kWh}.$

2.2

Für den Nenner des Bruchs $h(t)$ gilt für $t\to \infty,$ dass $1+4840,21\cdot \mathrm e^{-0,8\cdot t} \to 1.$

Für $t\to \infty$ gilt somit $h(t)\to \dfrac{1643,35}{1} = 1643,35$

Der Grenzwert der Funktion $h$ beträgt für $t\to \infty$ damit $1643,35.$

2.3

Bestimmung der Ableitung von $h$ im CAS und anschließende Berechnung der Stelle $t$ des Maximums von $\(h$ mit Hilfe des Befehls $\text{fMax(d1h(t),t)}$ im CAS liefert:

$t_{\text{max}} \approx 10,61$

Für den Funktionswert folgt:

$\(h$

Zum Zeitpunkt mit dem größten Wachstum steigt die in Hessen durch Photovoltaik gewonnene Energie somit um ca. $328,67$ Millionen $\text{kWh}$ pro Jahr.

3.1

Der Wert $\overline{E}$ gibt den Mittelwert der Funktion $h,$ das heißt die mittlere Energieerzeugung, im Intervall $[a;b]$ an. In $(2)$ wird das Integral mit Hilfe einer Stammfunktion $H(t)= \dfrac{A}{k}\cdot \ln \left(B+\mathrm e^{k \cdot t} \right)$ von $h$ umgeformt. In $(3)$ folgt die Einsetzung der Integrationsgrenzen in die Stammfunktion $H$ und der von $t$ unabhängige Faktor $\dfrac{A}{k}$ wird ausgeklammert.
Schlussendlich wird in $(4)$ der Term mithilfe der Logarithmengesetze vereinfacht.

3.2

Berechnung des Mittelwertes der Funktion $h$ im Intervall $[-5;15],$ also dem Wert $\overline{E}$ aus der letzten Teilaufgabe, liefert mit den Werten $a=-5, 

b=15,

A=1643,35, 

B =4840,21$ und $k=0,8$ folgendes Ergebnis:

Rechenweg anzeigen

$\overline{E} \approx 364,06$