A1 - Analysis

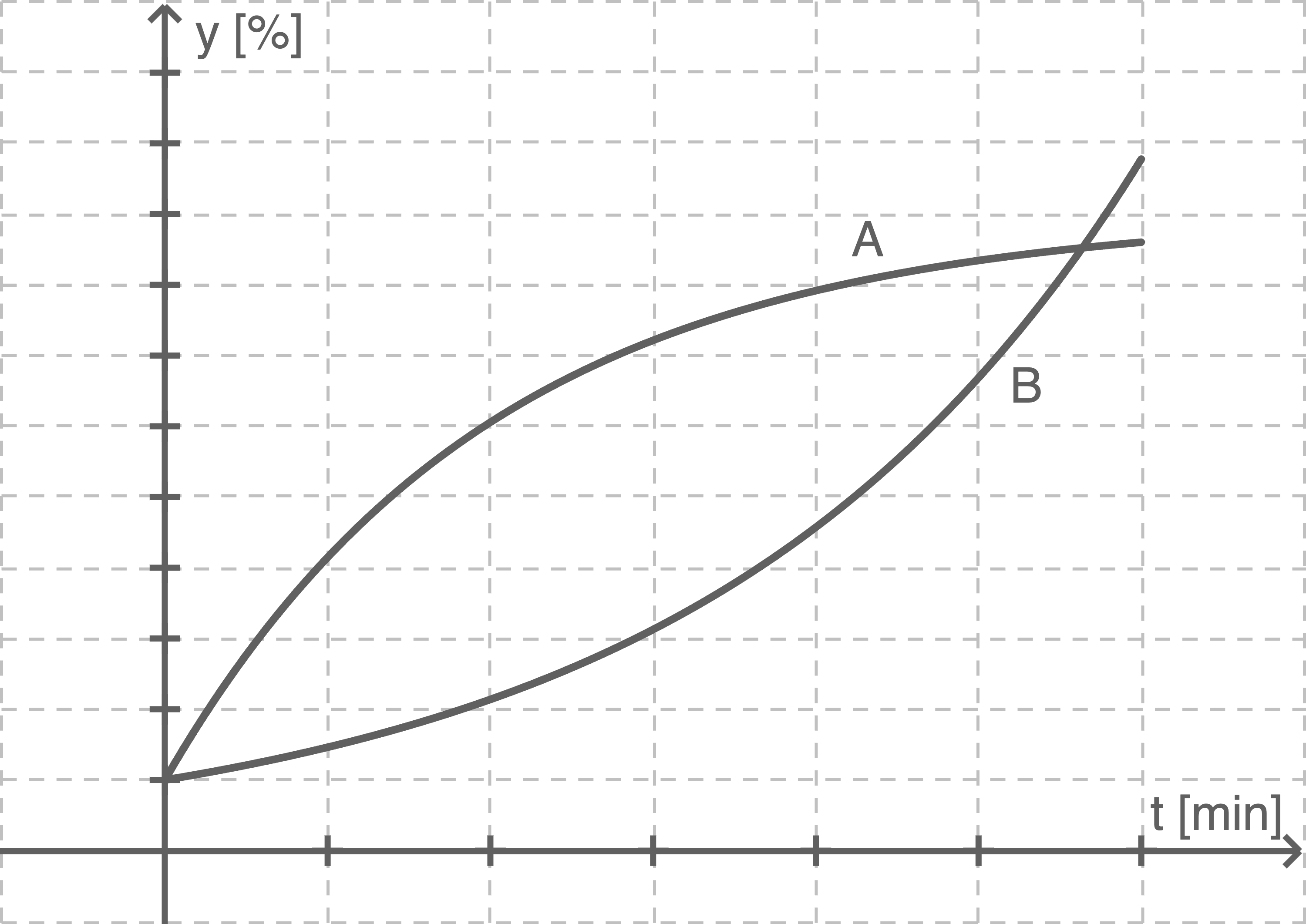
Eine Lernkurve beschreibt den Lernerfolg in Abhängigkeit von der Zeit. In der Abbildung sind Abschnitte zweier Lernkurven dargestellt. Dabei ist auf der horizontalen Achse die Zeit in Minuten abgetragen, während auf der vertikalen Achse der Lernerfolg als prozentualer Anteil des gelernten Stoffs dargestellt ist.

Die Kurven beschreiben den Lernerfolg zweier Schüler $S_1$ und $S_2$ während einer Lernphase für eine Klausur. Schüler $S_1$ kann am Anfang große Lernzuwächse verzeichnen, Schüler $S_2$ braucht einige Zeit, bis er sich in die Lernsituation eingefunden hat, der Lernerfolg nimmt aber immer stärker zu.

Koordinatensystem Lernkurven Hessen Mathe Abi 2014

1.1

Ordne die Lernkurven $A$ und $B$ den Schülern $S_1$ und $S_2$ begründet zu.

(3 BE)

1.2

Zum Graphen $A$ gehört die Funktionsgleichung $f$ mit $f(t)=90-80\cdot\mathrm e^{-0,05\cdot t}.$

Zu der anderen Lernkurve gehören die Werte der folgenden Tabelle:

$\color{#fff}{t \;\text{in min}}$	$\color{#fff}{y \;\text{in} \,\% }$
$0$	$10$
$15$	$18$
$30$	$31$
$55$	$81$

Ermittle eine geeignete Exponentialfunktion $g$ der Form $g(t)=a\cdot\mathrm e^{k\cdot t}$ .

$\bigg[$ Zur Kontrolle: $g(t)=10\cdot\mathrm e^{0,038\cdot t}\;\bigg]$

(5 BE)

1.3

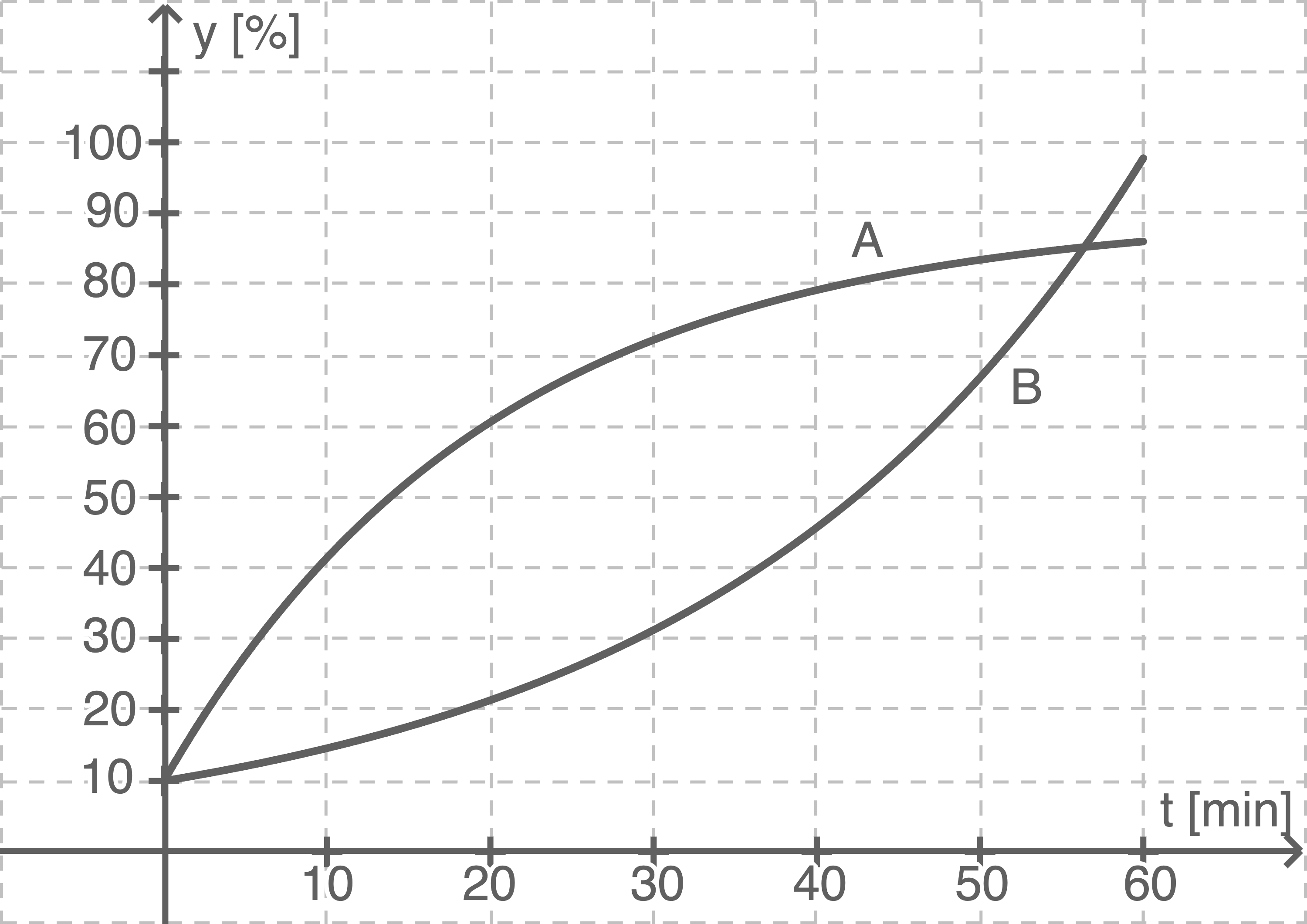
Bestimme, wie viel Prozent des Lernstoffes $S_1$ und $S_2$ nach 40 Minuten gelernt haben, und skaliere die Achsen in der Abbildung aus der Aufgabenstellung entsprechend.

(4 BE)

1.4

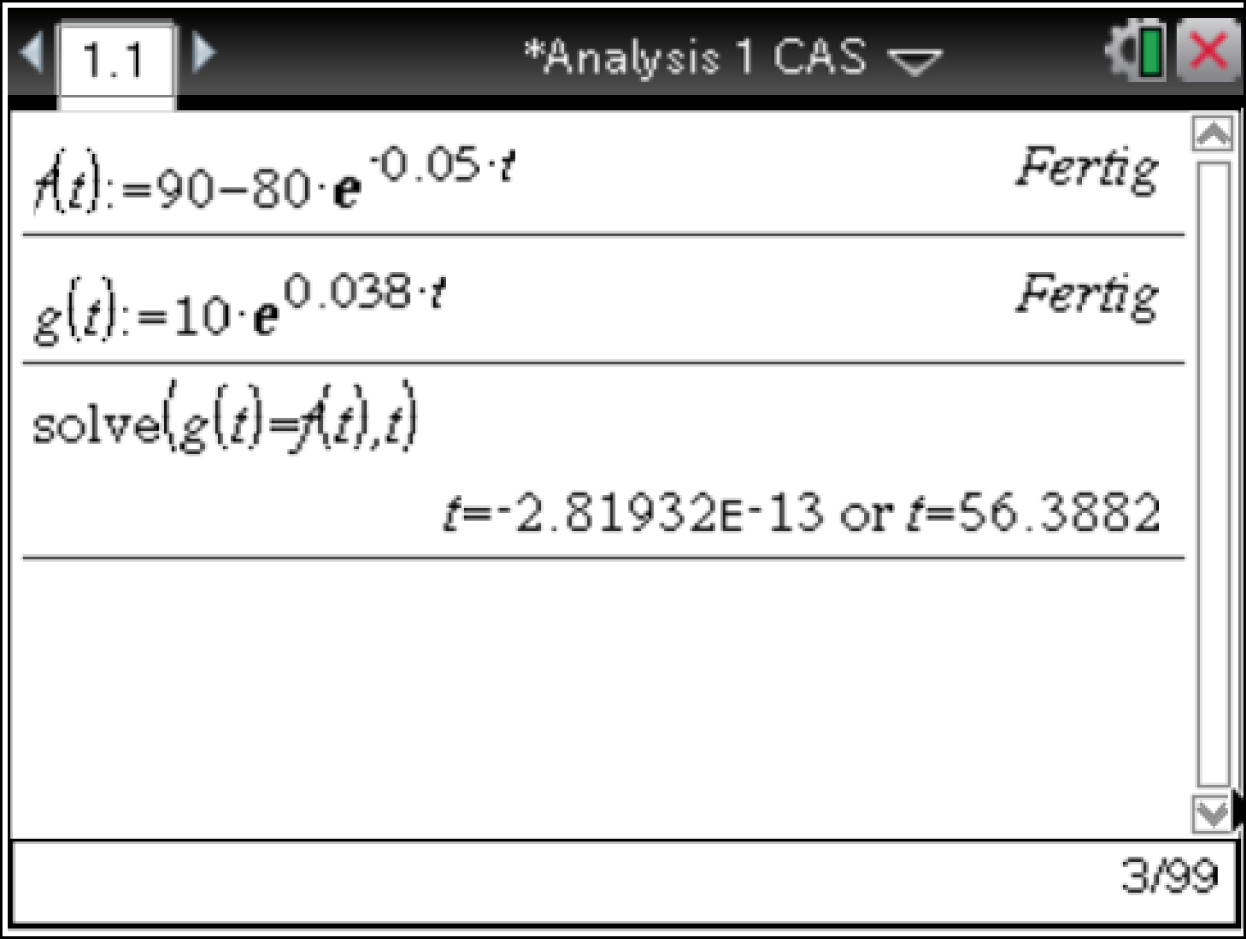
Ermittle den Zeitpunkt $t>0,$ an dem beide Schüler den gleichen Lernerfolg haben.

(2 BE)

Eine Mitschülerin behauptet: „Zu dem Zeitpunkt, an dem $S_1$ und $S_2$ dieselbe Lerngeschwindigkeit aufweisen, unterscheidet sich der Lernerfolg am stärksten.“

Berechne diese Lerngeschwindigkeit in $\dfrac{\%}{\text{min}}$ und die maximale Differenz des Lernerfolges.

Überprüfe daraufhin die Aussage der Mitschülerin.

(15 BE)

3.1

Begründe, dass der zu Graph $A$ gehörende Schüler ohne eine Änderung seines Lernverhaltens den Stoff während der Lernphase bis zur Klausur nicht zu einhundert Prozent gelernt haben wird.

(4 BE)

3.2

Der zu Graph $A$ gehörende Schüler plant eine neue Lernstrategie für die Klausur. Seine Überlegungen sind im folgenden Kasten dokumentiert.

$\(\begin{array}{ll} &\\ (\text{I})&m=\dfrac{100-f(t)}{60-t}=f$

Erläutere die Rechenschritte in den Zeilen $(\text{I})$ bis $(\text{III})$ und interpretiere diese im Sachzusammenhang.

(7 BE)

1.1

Der Graph $A$ steigt anfangs schneller an als Graph $B$ und gehört somit zu Schüler $S_1,$ der anfangs große Lernzuwächse verzeichnet. Graph $B$ beschreibt somit den Lernerfolg von Schüler $S_2,$ der anfangs langsamer steigt aber dann immer stärker zunimmt.

1.2

Einsetzen des ersten Wertepaars aus der Tabelle in die Exponentialfunktion aus der Augfgabenstellung liefert:

$\begin{array}[t]{rll} g(0)&=& 10& \\[5pt] a\cdot \mathrm e^{k\cdot 0}&=& 10& \\[5pt] a&=& 10 \end{array}$

Einsetzen des letzten Wertepaars aus der Tabelle ergibt nun:

$\begin{array}[t]{rll} g(55)&=& 81 & \\[5pt] a\cdot \mathrm e^{k\cdot 55}&=& 81 &\quad \scriptsize \mid\; a=10 \\[5pt] 10\cdot \mathrm e^{k\cdot 55}&=& 81&\quad \scriptsize \mid\; :10\\[5pt] \mathrm e^{k\cdot 55}&=& 8,1 &\quad \scriptsize \mid\; \ln(\;) \\[5pt] k\cdot 55&=& \ln(8,1)&\quad \scriptsize \mid\; :55\\[5pt] k&=& \dfrac{\ln(8,1)}{55}&\\[5pt] k&\approx& 0,038 \end{array}$

Eine geeignete Exponentialfunktion ist somit gegeben durch $g(t)=10\cdot \mathrm e^{0,038\cdot t}.$

1.3

Lernerfolg berechnen

$\begin{array}[t]{rll} f(40)&=& 90-80\cdot \mathrm e^{-0,05\cdot 40}&\quad \scriptsize \mid\; CAS \\[5pt] &\approx& 79,2 \end{array}$

$\begin{array}[t]{rll} g(40)&=& 10\cdot \mathrm e^{0,038\cdot 40}&\quad \scriptsize \mid\; CAS \\[5pt] &\approx& 45,7 \end{array}$

Nach 40 Minuten hat Schüler $S_1$ somit etwa $79,2\,\%$ und Schüler $S_2$ etwa $45,7\,\%$ des Lernsstoffs gelernt.

Achsen skalieren

1.4

Mathematische Gleichungen und Lösungen in einem CAS-Programm.

Der Zeitpunkt, an dem beide Schüler den gleichen Lernerfolg haben, entspricht der $t$ -Koordinate des Schnittpunkts der beiden Graphen $A$ und $B.$ Dieser kann mit dem CAS bestimmt werden.

Nach dem Definieren der beiden Funktionen $f$ und $g$ ergibt sich mit dem solve-Befehl:

menu 3 1

$\begin{array}[t]{rll} g(t)&=& f(t)&\quad \scriptsize \mid\; CAS \\[5pt] t_1&\approx& -2,8& \\[5pt] t_2&\approx& 56,4 \end{array}$

Da $t\gt0$ gelten soll, haben die beiden Schüler nach etwa 56 Minuten den gleichen Lernerfolg.

1. Schritt: Ableitungen bilden

Da die Funktionen $f$ und $g$ den Lernerfolg der beiden Schüler darstellen, wird die Lerngeschwindigkeit durch ihre ersten Ableitungen beschrieben.

Mit der Produkt- und Kettenregel folgen diese mit:

$\(\begin{array}[t]{rll} f$

$\(\begin{array}[t]{rll} g$

Alternativ können die Ableitungsfunktionen auch mit dem CAS unter menu $\to$ 4 $\to$ 1 bestimmt werden.

2. Schritt: Ableitungsfunktionen gleichsetzen

Mathematische Berechnungen und Gleichungen in einem CAS (Computer Algebra System) zur Analyse von Funktionen.

Der Zeitpunkt, an dem die beiden Schüler dieselbe Lerngeschwindigkeit aufweisen entspricht der $t$ -Koordinate des Schnittpunkts der beiden Ableitungsfunktionen $\(F$ und $\(g$

Gleichsetzen mit dem solve-Befehl des CAS ergibt:

$\(\begin{array}[t]{rll} f$

3. Schritt: $\boldsymbol{y}$ -Koordinate berechnen

Mit dem CAS folgt:

$\(f$

Nach etwa 26,7 Minuten ist die Lerngeschwindigkeit der beiden Schüler mit $1,05 \dfrac{\,\%}{\,\text{min}}$ gleich.

4. Schritt: Maximale Differenz des Lernerfolgs bestimmen

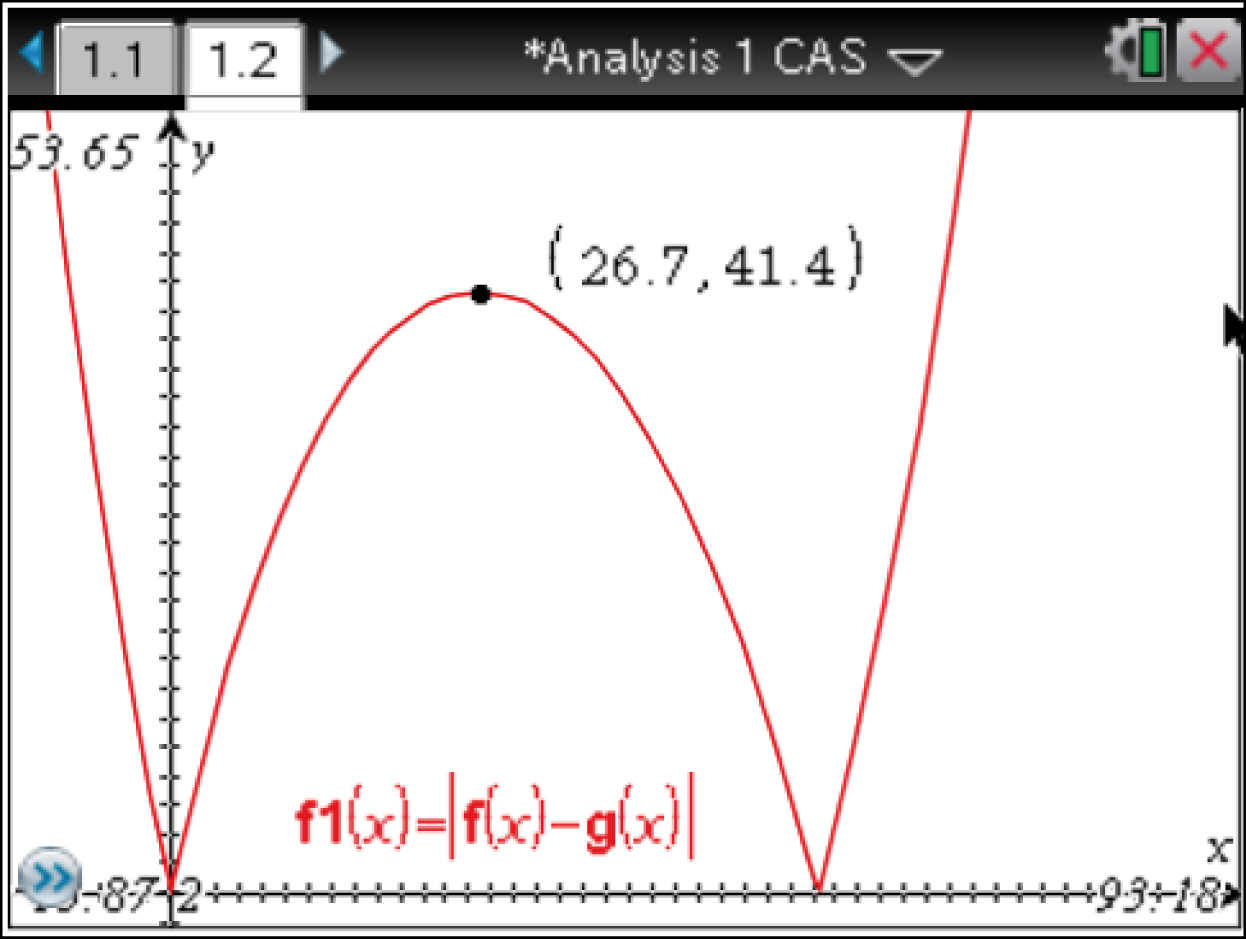Graph einer Funktion mit einer roten Kurve und einem markierten Punkt bei (26.7, 41.4).

Die maximale Differenz des Lernerfolgs ergibt sich mit $D(x)=|f(x)-g(x)|.$

Diese Differenzenfunktion kann mit dem CAS im Graph-Modus graphisch dargestellt werden.

Mit folgendem Befehl kann anschließend das Maximum bestimmt werden:

menu 6 3

Es folgt, dass der Lernerfolg der beiden Schüler nach ungefähr 26,7 Minuten die maximale Differenz aufweist.

Die Aussage der Mitschülerin ist somit korrekt:

Nach ungefähr 26,7 Minuten ist die Lerngeschwindigkeit der beiden Schüler gleich, aber die Differenz des Lernerfolges maximal.

3.1

Aus dem Graphen von $A$ geht hervor, dass sich dieser einem Grenzwert nähert. Dieser ergibt sich mit:

Da der Exponent der Exponentialfunktion für $t \to \infty$ negativ wird, konvergiert der gesamte Ausdruck $\mathrm{e}^{-0,05 \cdot t}$ für $t \to \infty$ gegen Null. Es gilt also:

$\begin{array}[t]{rll} \displaystyle\lim_{t \to \infty} f(t)&=& \displaystyle\lim_{t \to \infty} 90 - 80 \cdot \mathrm{e}^{-0,05 \cdot t}& \\[5pt] &=& 90-80\cdot 0& \\[5pt] &=& 90 \end{array}$

Alternativ kann der Grenzwert mit dem CAS durch den Befehl menu $\to$ 4 $\to$ 4 bestimmt werden.

Da der Graph von $f$ für $t \to \infty$ folglich gegen den Wert $90\,\%$ konvergiert, wird dieser Wert nie erreicht oder überschritten. Der Schüler $S_1$ kann den Stoff also während der Lernphase bis zur Klausur nicht zu $100\,\%$ lernen.

3.2

Rechenschritte erläutern

In Zeile $(\text{I})$ wird die Änderungsrate $m$ des Lernerfolges in Abhängigkeit von der Zeit definiert und mit der ursprünglichen Lerngeschwindigkeit $\(\,f$ gleichgesetzt.
Hierbei fällt bereits auf, dass der Schüler versucht, sich an den Wert 100 anzunähern, indem er die ursprüngliche Funktion $f(t)$ vom Wert 100 subtrahiert. $m$ stellt die neue Lerngeschwindigkeit dar.

In Zeile $(\text{II})$ werden nun die entsprechenden Funktionterme der Funktion $f(t)$ und der Ableitung $\(f$ eingesetzt und weitestgehend vereinfacht.

Zeile $(\text{III})$ liefert den berechneten Schnittpunkt der neuen Lerngeschwindigkeit $m$ und der ursprünglichen Lerngeschwindigkeit $\(\,f$ Nach ungefähr 29 Minuten sind die Lerngeschwindigkeiten der alten und neuen Lernkurve somit identisch mit einem Wert von $0,93 \dfrac{\,\%}{\text{min}}.$

Interpretation

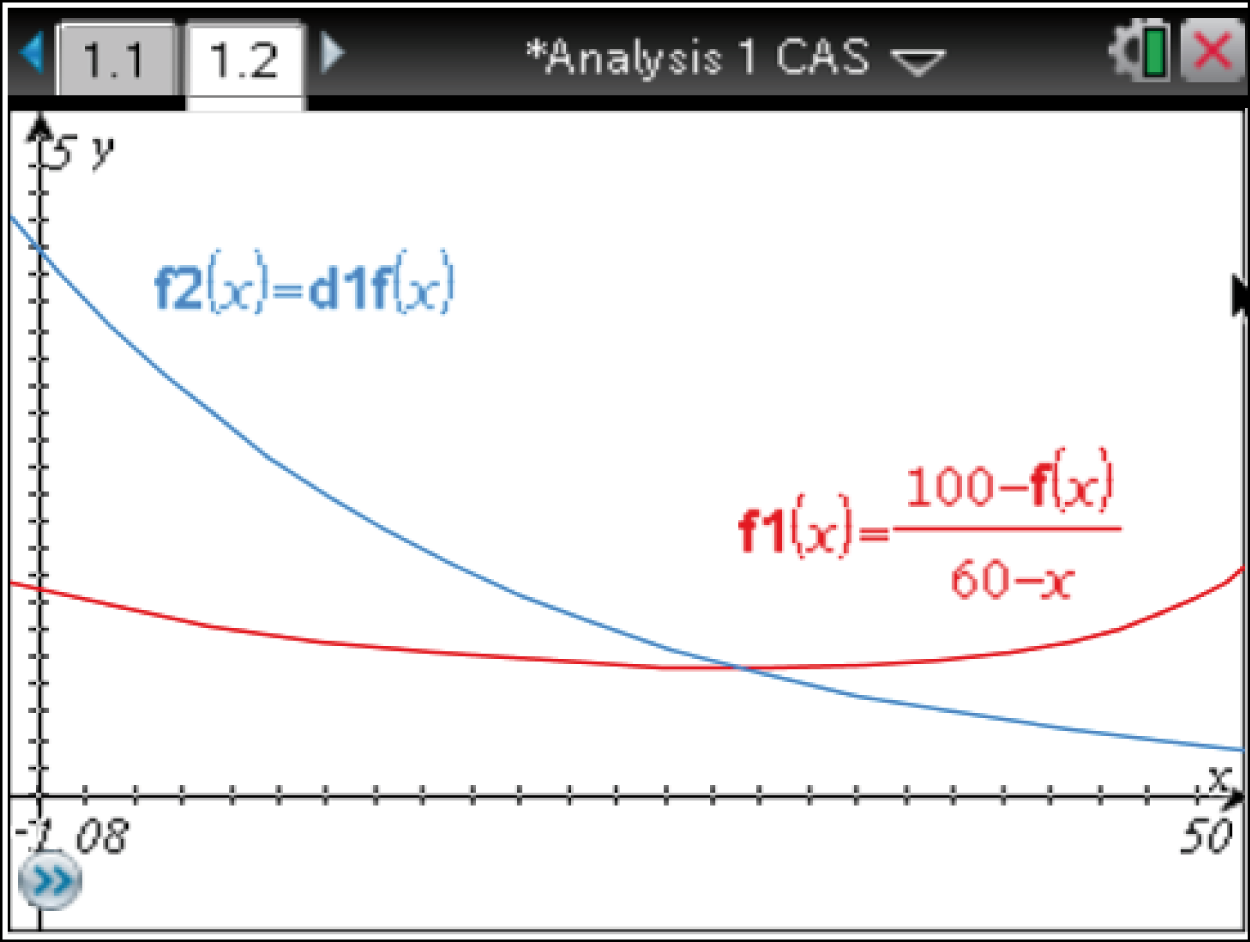Grafik mit zwei Funktionen f1(x) und f2(x) im Koordinatensystem.

Die beiden Funktionen können mit dem CAS graphisch dargestellt werden, sodass der Verlauf der Graphen um den Schnittpunkt herum klar wird.

Es kann abgelesen werden, dass die neu definierte Lerngeschwindigkeit ab $t \approx 29$ höher als die ursprüngliche Lerngeschwindigkeit $\(\,f$ ausfällt.

Die Graphen zeigen, dass die momentane Änderungsrate des Lernerfolgs, also die Steigung der Lernkurve, mit der alten Lernstrategie zu Beginn der Lernphase des Schülers $S_1$ hoch ist und dann mit der Zeit abnimmt und so nie $100\,\%$ erreicht. Die neuen Überlegungen des Schülers führen zu einem Zeitpunkt $t \approx 29$ Minuten, an dem die Steigung der Lernkurve wieder ansteigt.

Der Schüler plant durch die neue Strategie also, auch gegen Ende der Lernphase noch einen schnelleren und effizienteren Lernerfolg zu erzielen, indem er die Geschwindigkeit seiner Lernkurve nach dem Zeitpunkt $t \approx 29$ Minuten erneut steigert.

1.1

1.2

Einsetzen des ersten Wertepaars aus der Tabelle in die Exponentialfunktion aus der Augfgabenstellung liefert:

$\begin{array}[t]{rll} g(0)&=& 10& \\[5pt] a\cdot \mathrm e^{k\cdot 0}&=& 10& \\[5pt] a&=& 10 \end{array}$

Einsetzen des letzten Wertepaars aus der Tabelle ergibt nun:

Eine geeignete Exponentialfunktion ist somit gegeben durch $g(t)=10\cdot \mathrm e^{0,038\cdot t}.$

1.3

Lernerfolg berechnen

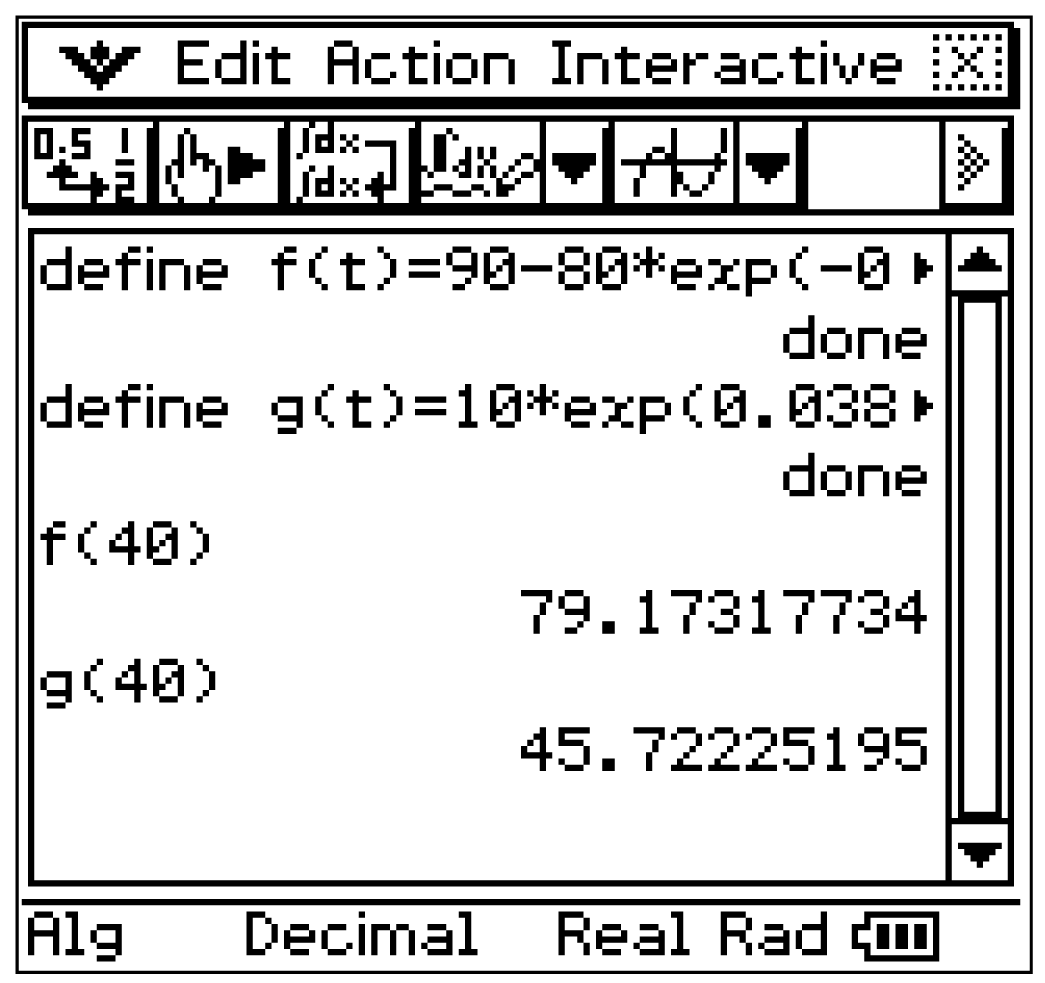
Bildschirmansicht eines mathematischen Programms mit Funktionsdefinitionen und Berechnungen.

$\begin{array}[t]{rll} f(40)&=& 90-80\cdot \mathrm e^{-0,05\cdot 40}&\quad \scriptsize \mid\; CAS \\[5pt] &\approx& 79,2 \end{array}$

$\begin{array}[t]{rll} g(40)&=& 10\cdot \mathrm e^{0,038\cdot 40}&\quad \scriptsize \mid\; CAS \\[5pt] &\approx& 45,7 \end{array}$

Nach 40 Minuten hat Schüler $S_1$ somit etwa $79,2\,\%$ und Schüler $S_2$ etwa $45,7\,\%$ des Lernsstoffs gelernt.

Achsen skalieren

1.4

Bildschirmansicht einer mathematischen Software mit Funktionen und Gleichungen zur Lösung von mathematischen Problemen.

Der Zeitpunkt, an dem beide Schüler den gleichen Lernerfolg haben, entspricht der $t$ -Koordinate des Schnittpunkts der beiden Graphen $A$ und $B.$ Dieser kann mit dem CAS bestimmt werden.

Nach dem Definieren der beiden Funktionen $f$ und $g$ ergibt sich mit dem solve-Befehl:

Interactive Advanced Solve

$\begin{array}[t]{rll} g(t)&=& f(t)&\quad \scriptsize \mid\; CAS \\[5pt] t_1&\approx& -2,8& \\[5pt] t_2&\approx& 56,4 \end{array}$

Da $t\gt0$ gelten soll, haben die beiden Schüler nach etwa 56 Minuten den gleichen Lernerfolg.

1. Schritt: Ableitungen bilden

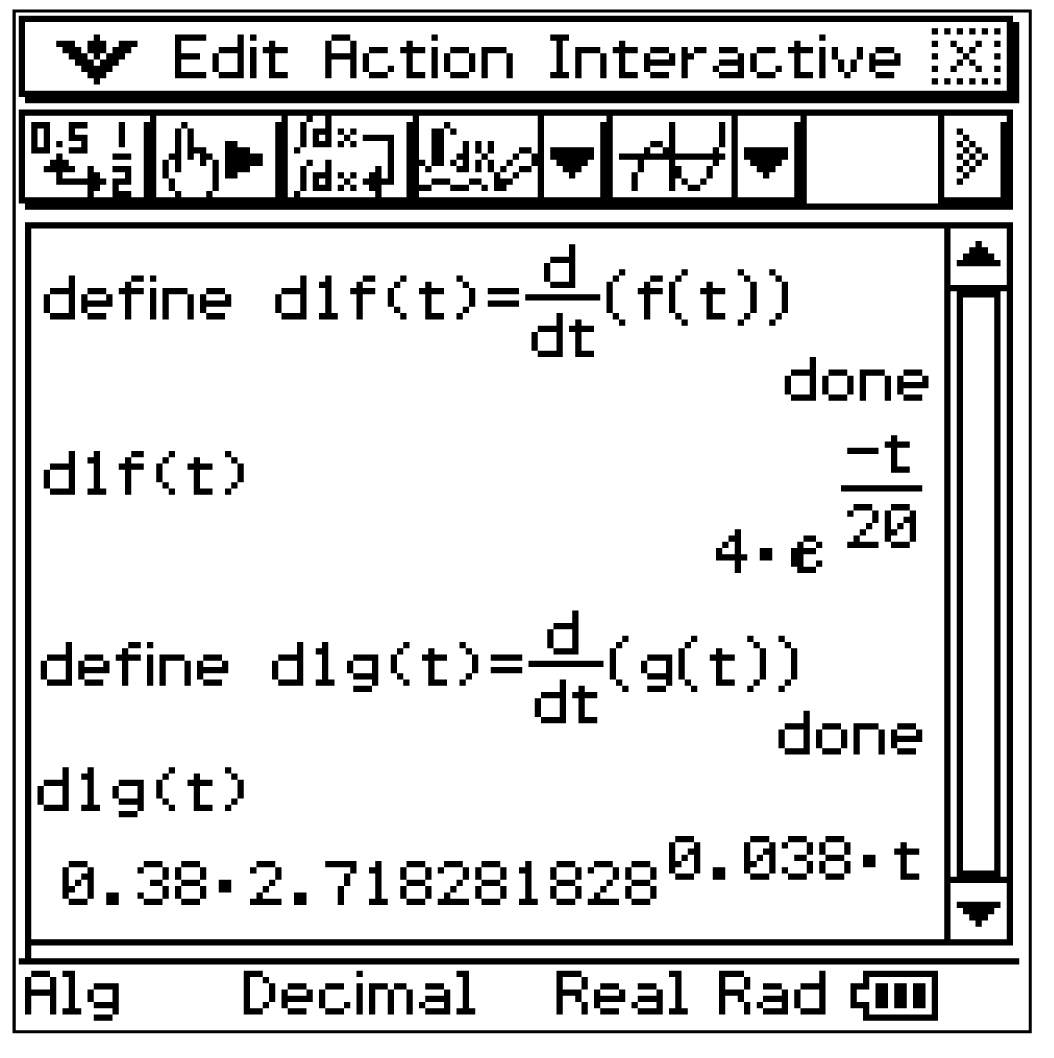Mathematische Software-Oberfläche mit Funktionen zur Ableitung und Eingabefenster.

Da die Funktionen $f$ und $g$ den Lernerfolg der beiden Schüler darstellen, wird die Lerngeschwindigkeit durch ihre ersten Ableitungen beschrieben.

Mit der Produkt- und Kettenregel folgen diese mit:

$\(\begin{array}[t]{rll} f$

$\(\begin{array}[t]{rll} g$

Alternativ können die Ableitungsfunktionen auch mit dem CAS unter menu $\to$ 4 $\to$ 1 bestimmt werden.

2. Schritt: Ableitungsfunktionen gleichsetzen

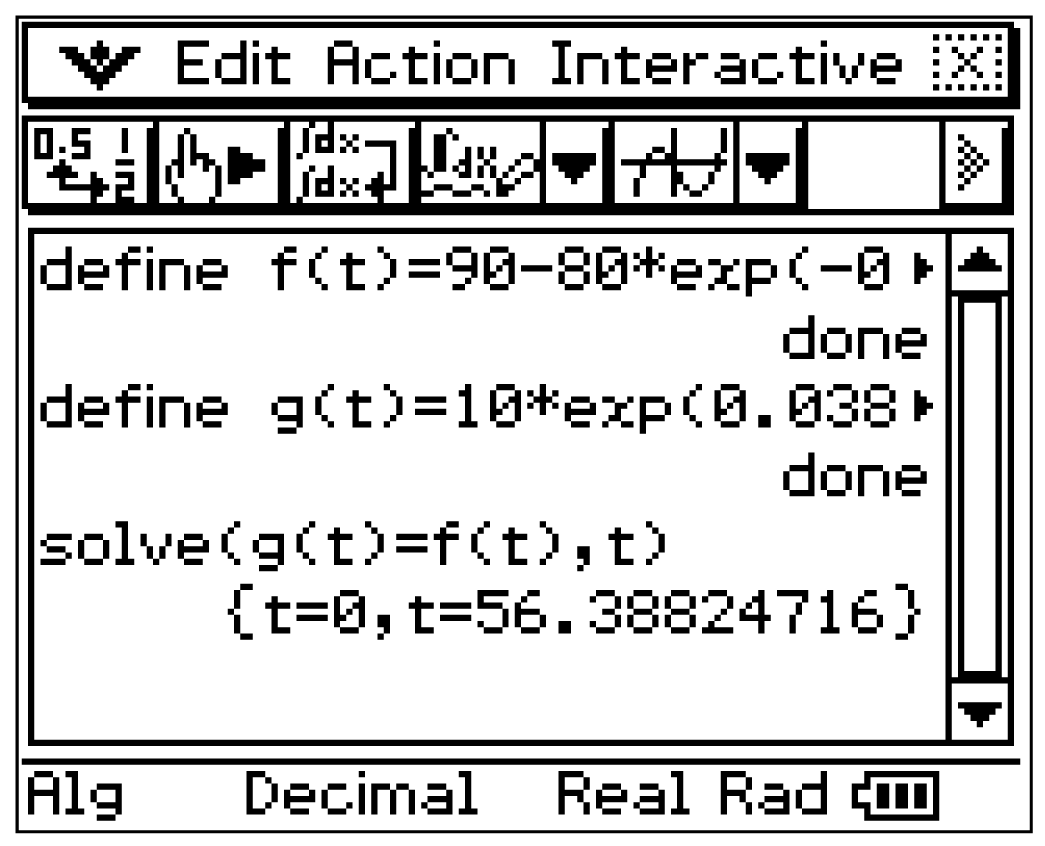
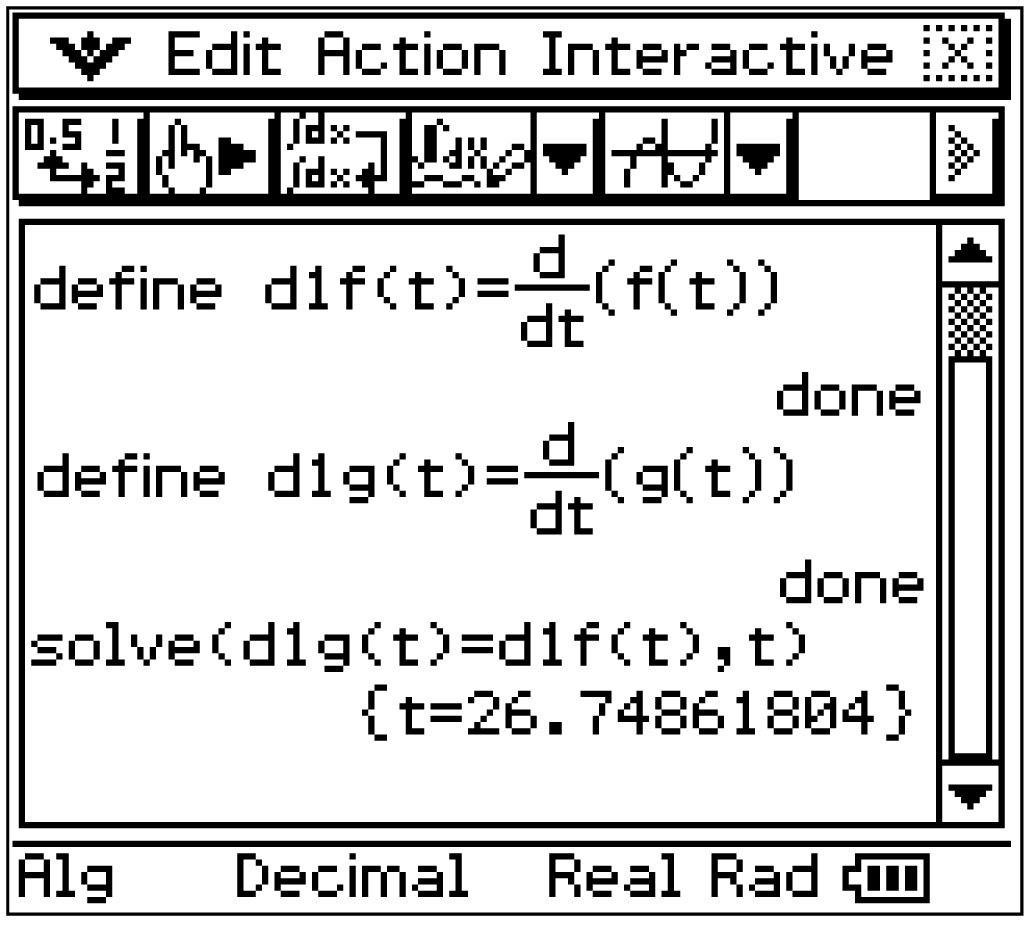Bildschirmansicht einer Software zur Definition und Lösung von mathematischen Funktionen.

Der Zeitpunkt, an dem die beiden Schüler dieselbe Lerngeschwindigkeit aufweisen entspricht der $t$ -Koordinate des Schnittpunkts der beiden Ableitungsfunktionen $\(F$ und $\(g$

Gleichsetzen mit dem solve-Befehl des CAS ergibt:

$\(\begin{array}[t]{rll} g$

3. Schritt: $\boldsymbol{y}$ -Koordinate berechnen

Mit dem CAS folgt:

$\(f$

Nach etwa 26,7 Minuten ist die Lerngeschwindigkeit der beiden Schüler mit $1,05 \dfrac{\,\%}{\,\text{min}}$ gleich.

4. Schritt: Maximale Differenz des Lernerfolgs bestimmen

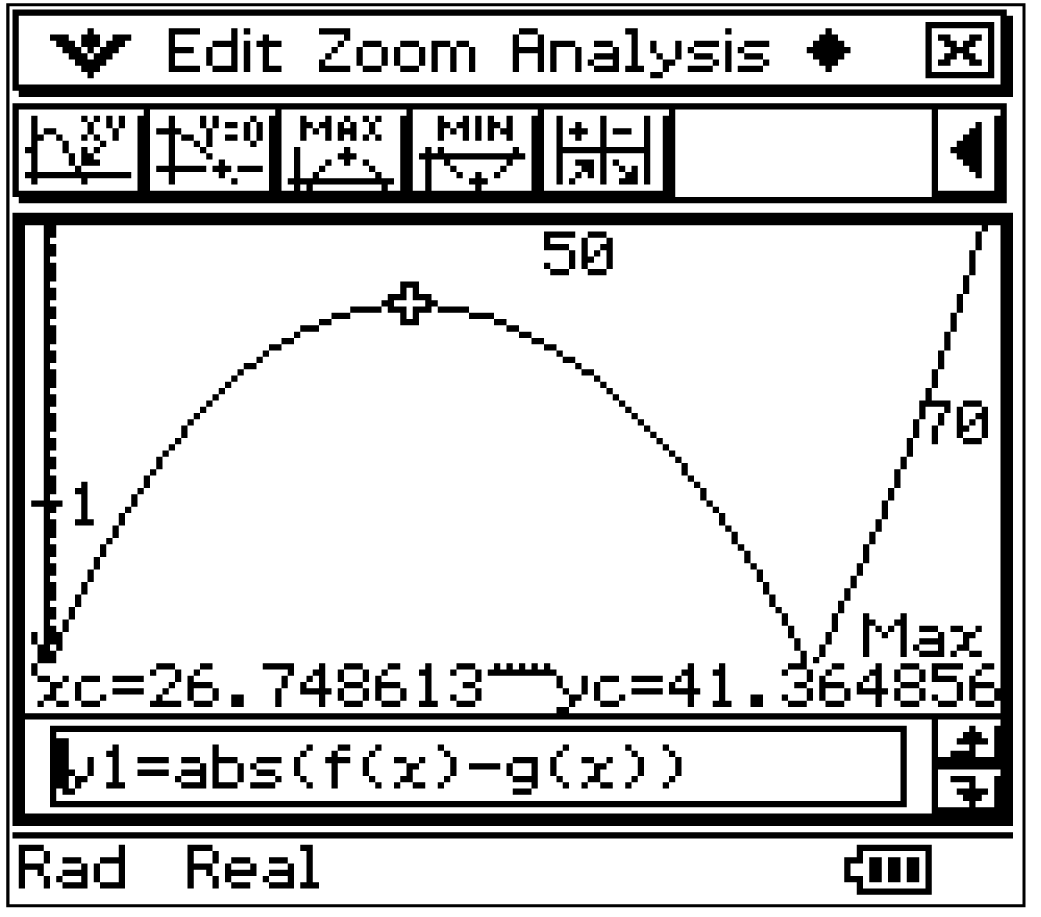Grafische Darstellung einer mathematischen Funktion mit Analyse-Tools und Koordinaten im Hintergrund.

Die maximale Differenz des Lernerfolgs ergibt sich mit $D(x)=|f(x)-g(x)|.$

Diese Differenzenfunktion kann mit dem CAS im Graph-Modus graphisch dargestellt werden.

Mit folgendem Befehl kann anschließend das Maximum bestimmt werden:

Analysis G-solve Max

Es folgt, dass der Lernerfolg der beiden Schüler nach ungefähr 26,7 Minuten die maximale Differenz aufweist.

Die Aussage der Mitschülerin ist somit korrekt:

Nach ungefähr 26,7 Minuten ist die Lerngeschwindigkeit der beiden Schüler gleich, aber die Differenz des Lernerfolges maximal.

3.1

Aus dem Graphen von $A$ geht hervor, dass sich dieser einem Grenzwert nähert. Dieser ergibt sich mit:

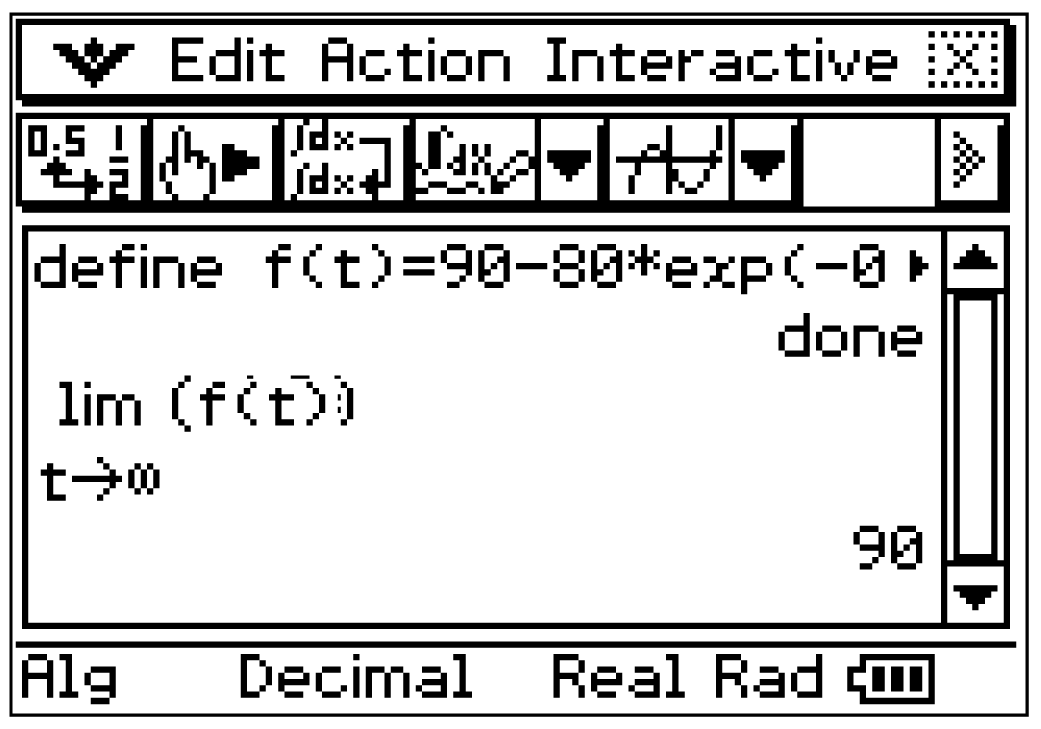Bildschirmansicht einer mathematischen Software mit einer Funktion und Grenzwertberechnung.

Da der Exponent der Exponentialfunktion für $t \to \infty$ negativ wird, konvergiert der gesamte Ausdruck $\mathrm{e}^{-0,05 \cdot t}$ für $t \to \infty$ gegen Null. Es gilt also:

$\begin{array}[t]{rll} \displaystyle\lim_{t \to \infty} f(t)&=& \displaystyle\lim_{t \to \infty} 90 - 80 \cdot \mathrm{e}^{-0,05 \cdot t}& \\[5pt] &=& 90-80\cdot 0& \\[5pt] &=& 90 \end{array}$

Alternativ kann der Grenzwert mit dem CAS durch den Befehl menu $\to$ 4 $\to$ 4 bestimmt werden.

3.2

Rechenschritte erläutern

In Zeile $(\text{II})$ werden nun die entsprechenden Funktionterme der Funktion $f(t)$ und der Ableitung $\(f$ eingesetzt und weitestgehend vereinfacht.

Interpretation

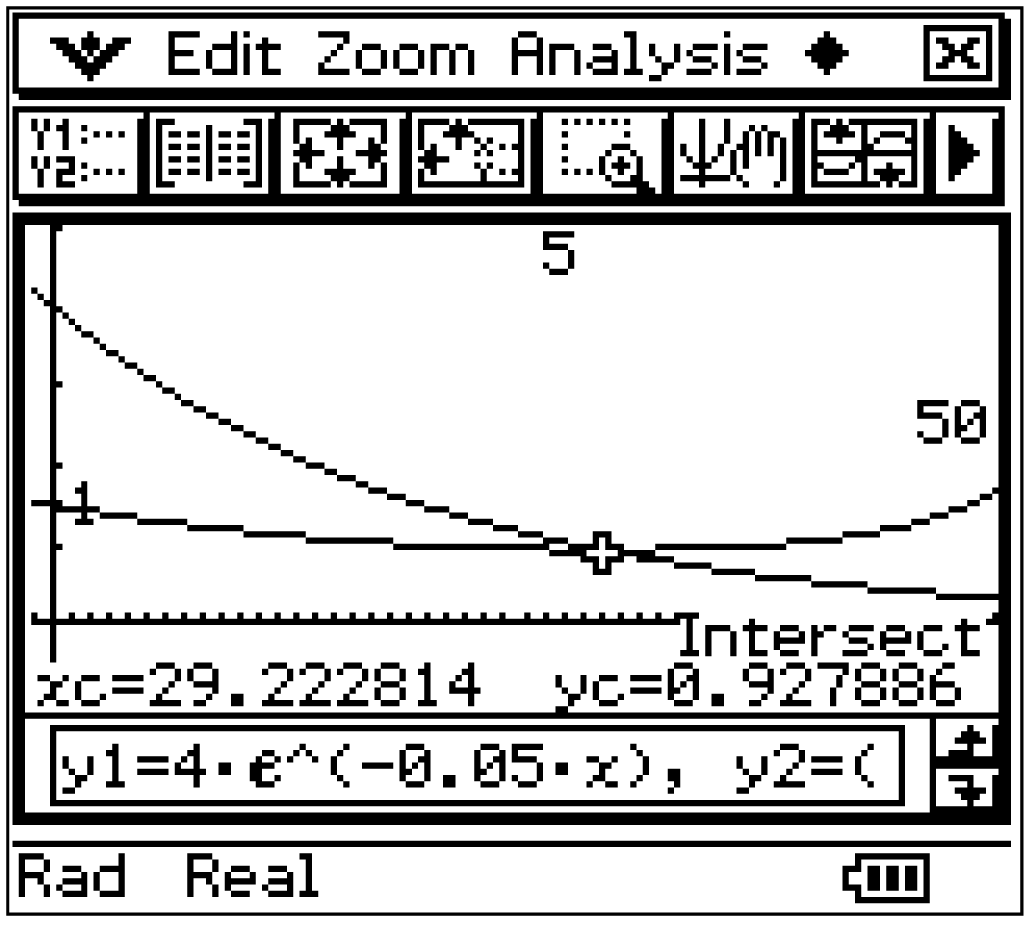Grafische Darstellung einer mathematischen Funktion mit interaktiven Analysewerkzeugen.

Die beiden Funktionen können mit dem CAS graphisch dargestellt werden, sodass der Verlauf der Graphen um den Schnittpunkt herum klar wird.

Es kann abgelesen werden, dass die neu definierte Lerngeschwindigkeit ab $t \approx 29$ höher als die ursprüngliche Lerngeschwindigkeit $\(\,f$ ausfällt.