A - Hilfsmittelfreier Teil

Analysis - Niveau 1

Gegeben ist die Funktion $f$ mit $f ( x )=\dfrac{3}{4} x ^2+\dfrac{1}{2}$ . Der Graph von $f$ ist in der Abbildung im Material dargestellt.

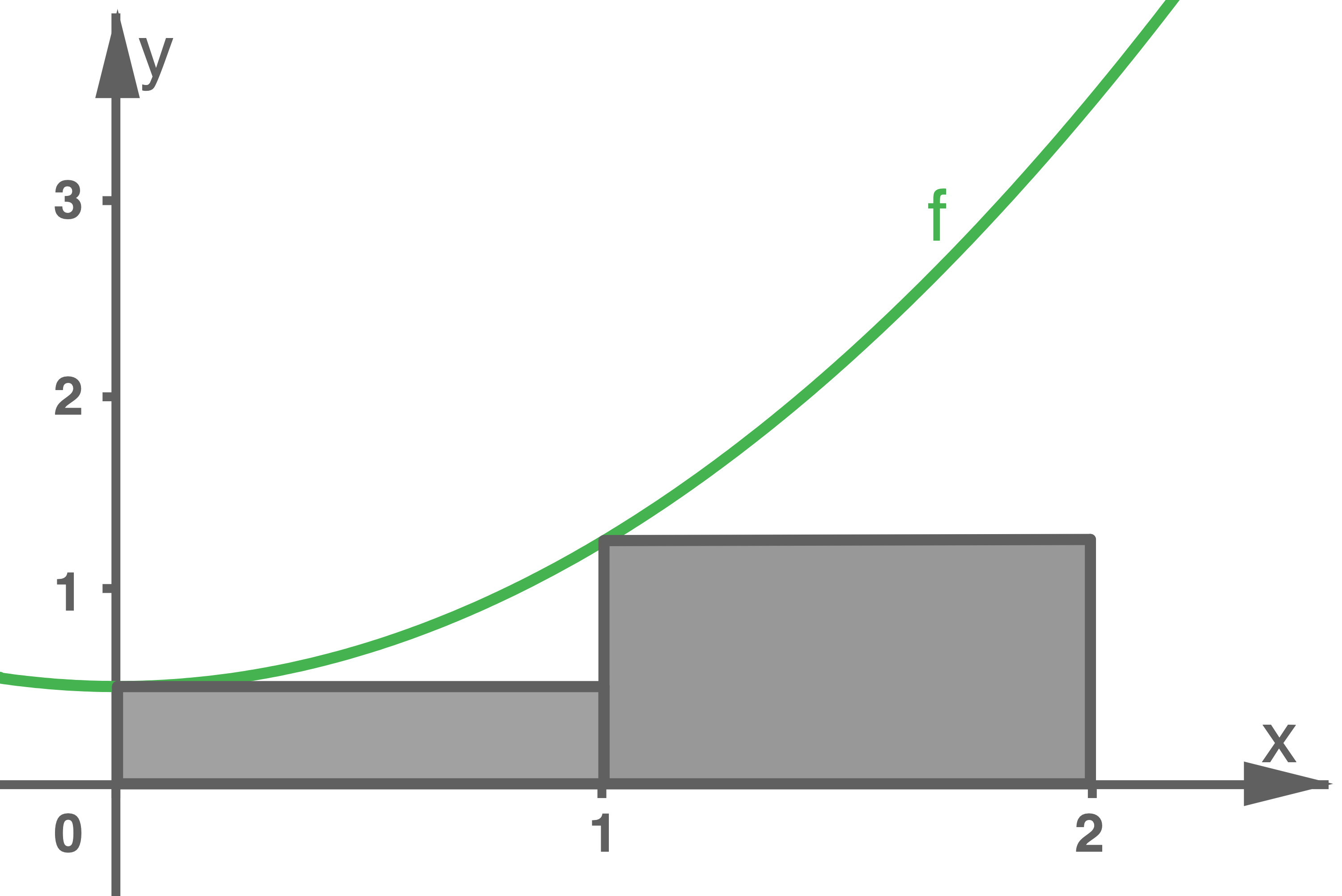
he mathe abi gk wtr 2022 abbildung graph f

Material

1.1

Berechne den Inhalt der Fläche zwischen dem Graphen von $f$ und der $x$ -Achse im Intervall $[0 ; 2]$ näherungsweise durch den Flächeninhalt der im Material eingezeichneten Rechtecke.

(2 BE)

1.2

Berechne den exakten Wert des Inhalts der Fläche zwischen dem Graphen von $f$ und der $x$ -Achse im Intervall $[0 ; 2]$ .

(2 BE)

1.3

Lea ist der Meinung, dass die Näherung sehr ungenau ist. Sie behauptet: „Der Näherungswert aus Aufgabe 1.1 weicht um mehr als $30 \,\%$ vom exakten Wert aus Aufgabe 1.2 ab.“
Gib an, ob Leas Behauptung wahr oder falsch ist.

(1 BE)

Stochastik - Niveau 1

Zwei Schützen zielen auf eine Scheibe.

2.1

Schütze 1 trifft die Scheibe mit einer Trefferwahrscheinlichkeit von $p _1=\dfrac{2}{3}$ . Berechne die Wahrscheinlichkeit dafür, dass er bei drei Schüssen die Scheibe mindestens zweimal trifft.

(3 BE)

2.2

Bei Schütze 2 beträgt die Wahrscheinlichkeit, dass er bei zwei Schüssen die Scheibe beide Male trifft, $\dfrac{9}{25}$ . Bestimme seine Trefferwahrscheinlichkeit $p _2$ .

(2 BE)

Lineare Algebra/Analytische Geometrie - Niveau 1

In einem mathematischen Modell wird im Punkt $A (1\mid -3\mid 0)$ senkrecht zum Erdboden ein $10$ Meter hoher Fahnenmast errichtet. Der Erdboden befindet sich in der $x$ - $y$ -Ebene, wobei eine Längeneinheit einem Meter entspricht. Die Koordinaten des Schattenpunktes $S$ der Mastspitze auf dem Boden zu einem bestimmten Zeitpunkt lauten $S (9\mid 3\mid 0)$ .

3.1

Berechne die Länge des Schattens des Fahnenmastes auf dem Boden.

(2 BE)

3.2

Ermittle einen Vektor, der die Richtung der Sonnenstrahlen beschreibt.

(2 BE)

3.3

Zu einem anderen Zeitpunkt ändert sich die $z$ -Koordinate des Sonnenstrahlvektors bei gleichbleibender $x$ - und $y$ -Koordinate so, dass der Schatten des Fahnenmastes auf dem Boden länger wird. Gib ein mögliches Beispiel für einen solchen Sonnenstrahlvektor an.

(1 BE)

Lineare Algebra/Analytische Geometrie - Niveau 2

Die Positionen zweier hier vereinfachend als punktförmig angenommener Rettungshubschrauber 1 und 2 können während ihrer gleichzeitig stattfindenden Flüge im Zeitraum $0 \leq t \leq 4$ durch die Koordinaten $H_1(2 t +4\mid 2 t +5\mid 0,3)$ und $H_2(3 t +4\mid 2 t +2\mid 0,3)$ beschrieben werden, wobei eine Längeneinheit $1\,\text{km}$ entspricht und $t$ die Zeit in Minuten angibt.

4.1

Die beiden Rettungshubschrauber bewegen sich im betrachteten Zeitraum auf geradlinigen Flugrouten. Gib die entsprechende Geradengleichung für Hubschrauber 1 an.

(1 BE)

4.2

Leite die Formel $d =\sqrt{ t ^2+9}$ für den Abstand der beiden Hubschrauber in Abhängigkeit von der Zeit $t$ her.

(2 BE)

4.3

Begründe mithilfe der Formel aus Aufgabe 4.2 ohne weitere Rechnung, zu welchem Zeitpunkt der Abstand der beiden Hubschrauber im betrachteten Zeitraum maximal ist.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Analysis - Niveau 1 - Lösung

1.1

Rechteck im Intervall $[0;1]$

$\begin{array}[t]{rll} f(0)&=&\dfrac{3}{4} \cdot 0 ^2+\dfrac{1}{2} &=&\dfrac{1}{2} \end{array}$

$\begin{array}[t]{rll} A_1&=& 1\cdot \dfrac{1}{2} &=&\dfrac{1}{2} \;[\,\text{FE}] \end{array}$

Rechteck im Intervall $[1;2]$

$\begin{array}[t]{rll} f(1)&=&\dfrac{3}{4} \cdot 1 ^2+\dfrac{1}{2} &=&\dfrac{5}{4} \end{array}$

$\begin{array}[t]{rll} A_1&=& 1\cdot \dfrac{5}{4} &=&\dfrac{5}{4} \;[\,\text{FE}] \end{array}$

Der näherungsweise berechnete Flächeninhalt entspricht folglich $\dfrac{1}{2}+\dfrac{5}{4}= \dfrac{7}{4} \;\,\text{FE}.$

1.2

Rechenweg anzeigen

$\displaystyle\int_{0}^{2}f(x)\;\mathrm dx= 3 \;[\,\text{FE}]$

Der exakte Wert des Flächeninhalts zwischen dem Graphen von $f$ und der $x$ -Achse beträgt somit $3 \;\,\text{FE}.$

1.3

$30\,\%$ des exakten Werts aus 1.2:

$0,3\cdot 3 =0,9 \;[\,\text{FE}]$

Abweichung des Näherungswerts aus 1.1:

$3-\dfrac{7}{4}=\dfrac{5}{4}=1,25 \;[\,\text{FE}]$

Da der Näherungswert um mehr als $0,9 \;\,\text{FE}$ und somit um mehr als $30\,\%$ vom exakten Wert abweicht, ist Leas Behauptung wahr.

Stochastik - Niveau 1 - Lösung

2.1

$\begin{array}[t]{rll} P (k\geq2) &=& 3\cdot \left(\dfrac{2}{3} \right)^2\cdot \dfrac{1}{3} + \left(\dfrac{2}{3} \right)^3& \\[5pt] &=&\dfrac{4}{9} + \dfrac{8}{27}& \\[5pt] &=&\dfrac{20}{27} \end{array}$

Die Wahrscheinlichkeit, dass der Schütze 1 bei drei Schüssen mindestens zweimal trifft, beträgt somit $\dfrac{20}{27}.$

2.2

$\begin{array}[t]{rll} P(k=2)&=& (p_2)^2 & \\[5pt] \dfrac{9}{25}&=& (p_2)^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt] \dfrac{\sqrt{9}}{\sqrt{25}}&=& p_2 \\[5pt] \dfrac{3}{5}&=& p_2 &\\[5pt] \end{array}$

Lineare Algebra/Analytische Geometrie - Niveau 1 - Lösung

3.1

$\begin{array}[t]{rll} |\overrightarrow{AS}|&=&\left|\pmatrix{9-1\\3-(-3)\\0-0}\right| & \\[5pt] &=&\sqrt{8^2+6^2+0^2} & \\[5pt] &=&\sqrt{100} & \\[5pt] &=& 10 \; [\,\text{m}] \end{array}$

Der Schatten des Fahnenmasts auf dem Boden ist $10 \,\text{m}$ lang.

3.2

Koordinaten der Mastspitze $M$ bestimmen

Da der Mast $10 \,\text{m}$ hoch ist und senkrecht zur $xy$ -Ebene steht, folgt: $\overrightarrow{OM}=\pmatrix{1\\-3\\10}.$

Richtungsvektor $\overrightarrow{s}$ der Sonnenstrahlen ermitteln

$\begin{array}[t]{rll} \overrightarrow{s}&=&\overrightarrow{OS}-\overrightarrow{OM} & \\[5pt] &=&\pmatrix{9\\3\\0}- \pmatrix{1\\-3\\10}& \\[5pt] &=&\pmatrix{8\\6\\-10} \end{array}$

3.3

Je kleiner der Betrag der $z$ -Koordinate, desto flacher fallen die Sonnenstrahlen ein.

Damit der Schatten auf dem Boden länger wird, muss der Betrag der $z$ -Koordinate folglich kleiner werden.

Ein möglicher Vektor solch eines Sonnenstrahls ist somit beispielsweise $s_1=\pmatrix{8\\6\\-5}.$

Lineare Algebra/Analytische Geometrie - Niveau 2 - Lösung

4.1

Die Geradengleichung des Hubschrauber 1 kann aus den Koordinaten von $H_1$ gebildet werden:

$g_1: \overrightarrow{x}=\pmatrix{4\\5\\0,3}+t\cdot \pmatrix{2\\2\\0}$

4.2

$\begin{array}[t]{rll} \overrightarrow{H_1H_2}&=&\pmatrix{3t+4\\2t+2\\0,3}- \pmatrix{2t+4\\2t+5\\0,3}& \\[5pt] &=&\pmatrix{3t+4-2t-4\\2t+2-2t-5\\0,3-0,3}& \\[5pt] &=&\pmatrix{t\\-3\\0} \end{array}$

$\begin{array}[t]{rll} d=|\overrightarrow{H_1H_2}|&=& \sqrt{t^2+(-3)^2+0^2}& \\[5pt] &=&\sqrt{t^2+9} \end{array}$

4.3

Aus der Formel aus 4.2 folgt, dass der Abstand der Hubschrauber größer wird, wenn $t$ größer wird.

Da der Flug im Zeitraum $0\leq t\leq4$ betrachtet wird, ist der Abstand der beiden Hubschrauber somit zum Zeitpunkt $t=4$ am größten.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?