A2 - Analysis
In Herr Maiers Garten steht ein Kirschbaum. Beim Einpflanzen hatte der Baum eine Höhe von 2 Metern. 7 Jahre nach dem Einpflanzen ist er 5 Meter hoch.
Zur Modellierung seines Wachstums soll die Höhe des Kirschbaums durch eine Funktion in Abhängigkeit von der Zeit  beschrieben werden. Dazu werden die Funktionen
beschrieben werden. Dazu werden die Funktionen  und
und  vorgeschlagen mit
vorgeschlagen mit
 und
und 
 Dabei werden
Dabei werden  in Jahren seit dem Einpflanzzeitpunkt und
in Jahren seit dem Einpflanzzeitpunkt und  bzw.
bzw.  in Metern angegeben. Für die Modellierung gilt jeweils
in Metern angegeben. Für die Modellierung gilt jeweils  Für die Aufgaben 1.1 und 3 soll diese Einschränkung des Definitionsbereichs nicht gelten.
Für die Aufgaben 1.1 und 3 soll diese Einschränkung des Definitionsbereichs nicht gelten.
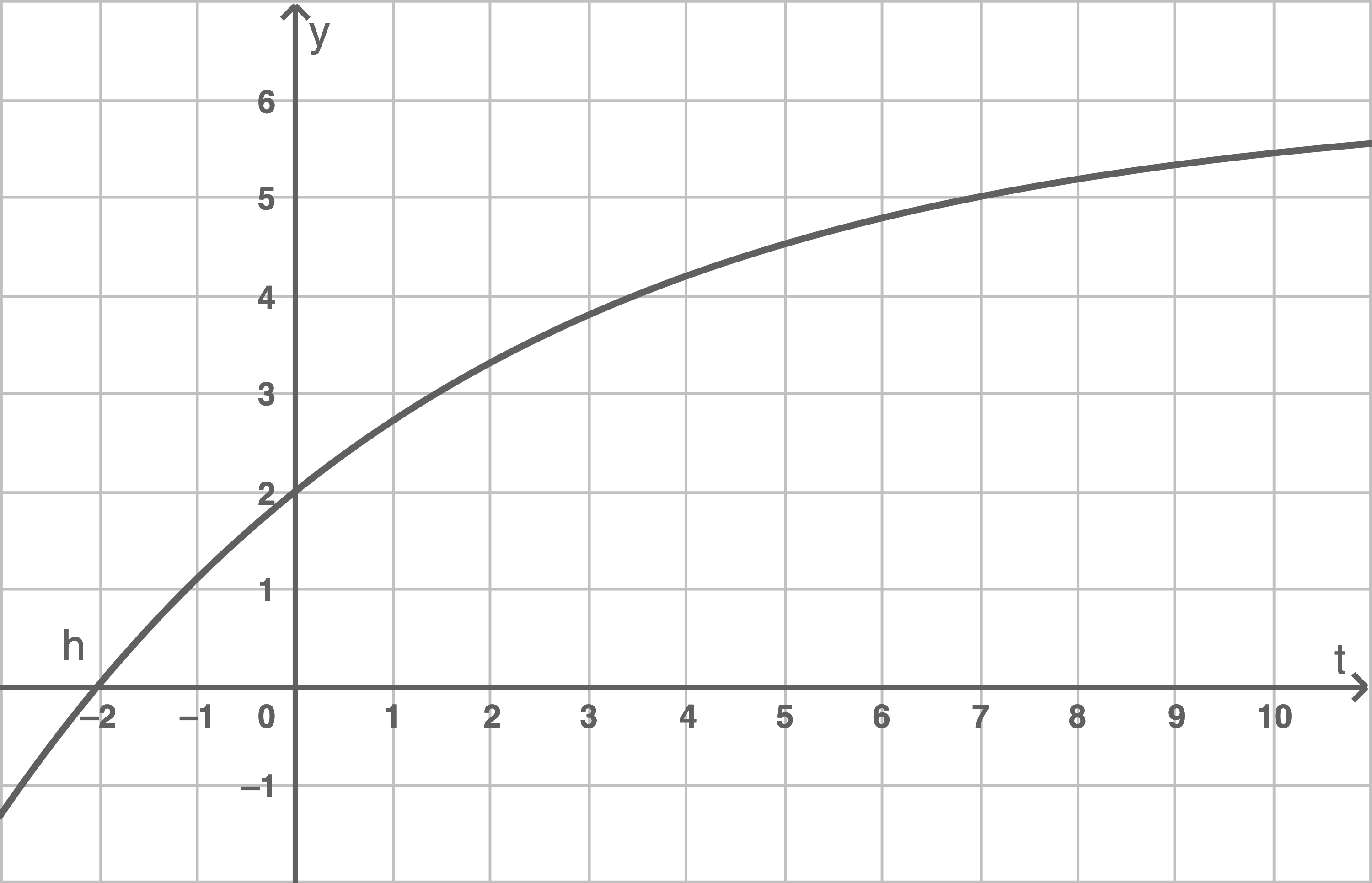

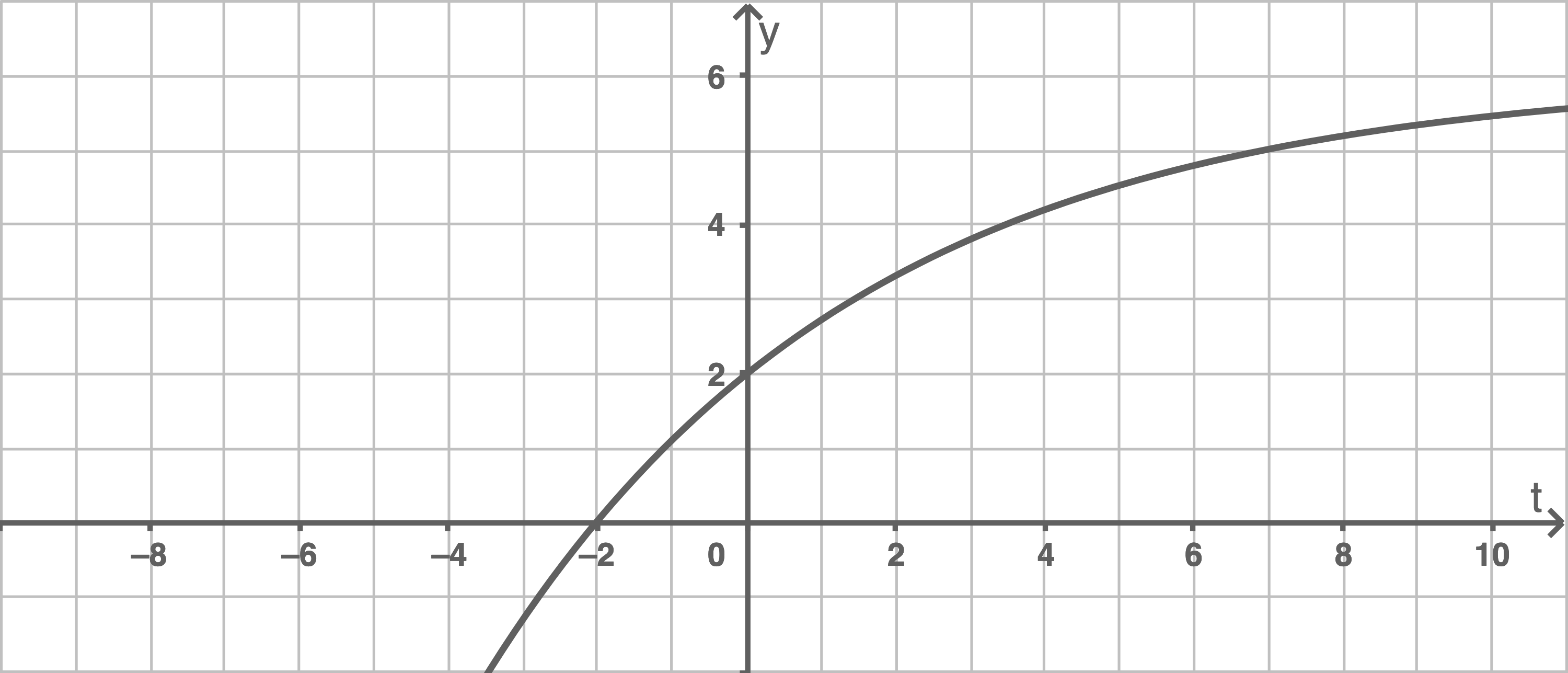

1.1
Im nebenstehenden Koordinatensystem ist der Graph von  abgebildet.
Zeichne zusätzlich den Graphen von
abgebildet.
Zeichne zusätzlich den Graphen von  in dieses Koordinatensystem.
in dieses Koordinatensystem.

(2 BE)
1.2
Beschreibe anhand der Graphen von  und
und  jeweils den Verlauf der Steigung.
Begründe im Sachzusammenhang ohne weitere Rechnung, warum die Funktion
jeweils den Verlauf der Steigung.
Begründe im Sachzusammenhang ohne weitere Rechnung, warum die Funktion  für die Modellierung des Wachstums des Kirschbaums auf lange Sicht besser geeignet ist als die Funktion
für die Modellierung des Wachstums des Kirschbaums auf lange Sicht besser geeignet ist als die Funktion 
(4 BE)
2.1
Begründe anhand des Funktionsterms der Funktion  dass sich die Höhe des Baums langfristig dem Wert von
dass sich die Höhe des Baums langfristig dem Wert von  immer mehr nähert, ohne ihn jedoch zu erreichen bzw. zu überschreiten.
immer mehr nähert, ohne ihn jedoch zu erreichen bzw. zu überschreiten.
(3 BE)
2.2
Berechne für die Modellierung mit der Funktion  den Zeitpunkt
den Zeitpunkt  zu dem die Höhe des Kirschbaums
zu dem die Höhe des Kirschbaums  des Werts aus Aufgabe 2.1 erreicht.
des Werts aus Aufgabe 2.1 erreicht.
(4 BE)
2.3
Bestimme die Gleichung der Ableitungsfunktion  Gib den Wert von
Gib den Wert von  an und deute diesen im Sachzusammenhang.
an und deute diesen im Sachzusammenhang.
(5 BE)
3
Im Folgenden wird der Graph der Funktion  mit
mit  schrittweise durch jeweils eine der geometrischen Abbildungen Streckung in
schrittweise durch jeweils eine der geometrischen Abbildungen Streckung in  -Richtung, Verschiebung in
-Richtung, Verschiebung in  -Richtung, Spiegelung an der
-Richtung, Spiegelung an der  -Achse und Spiegelung an der
-Achse und Spiegelung an der  -Achse in den Graphen der Funktion
-Achse in den Graphen der Funktion  überführt:
überführt:
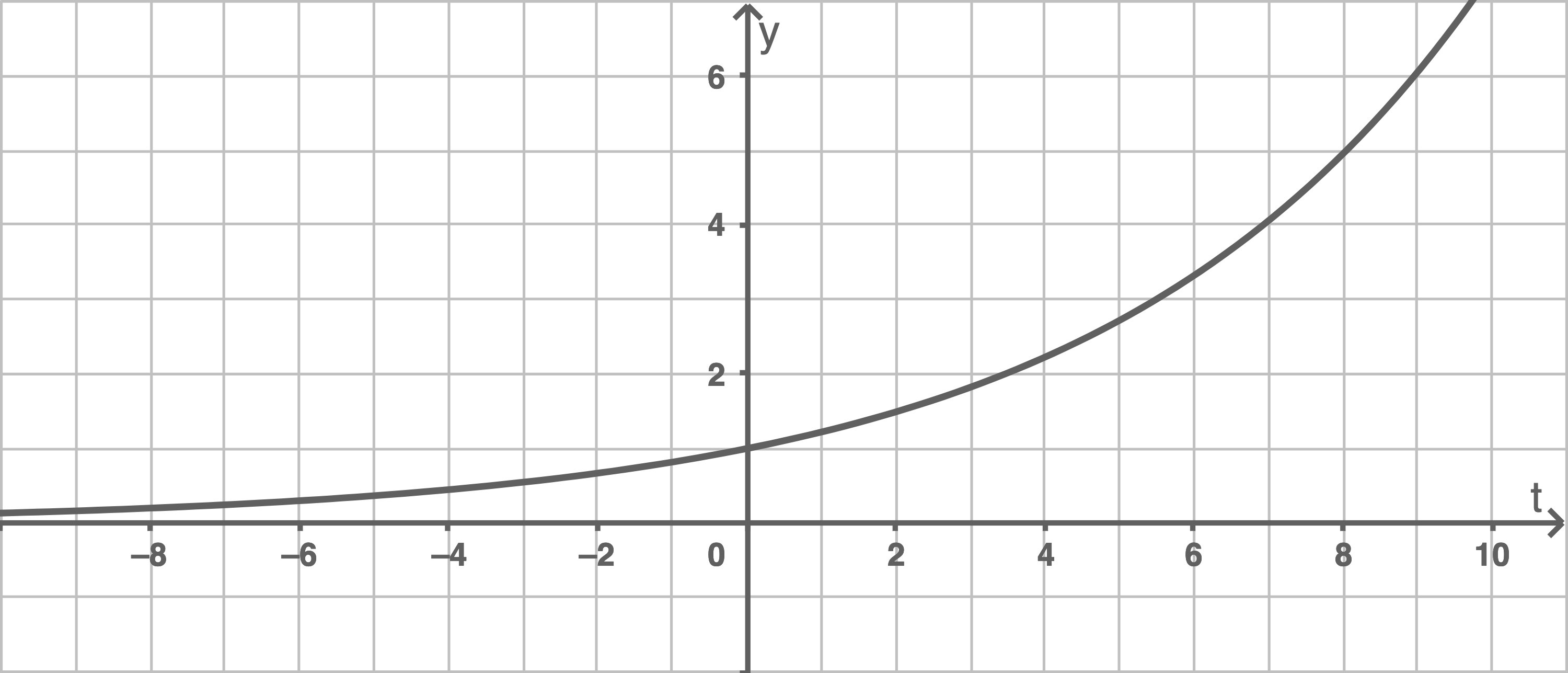

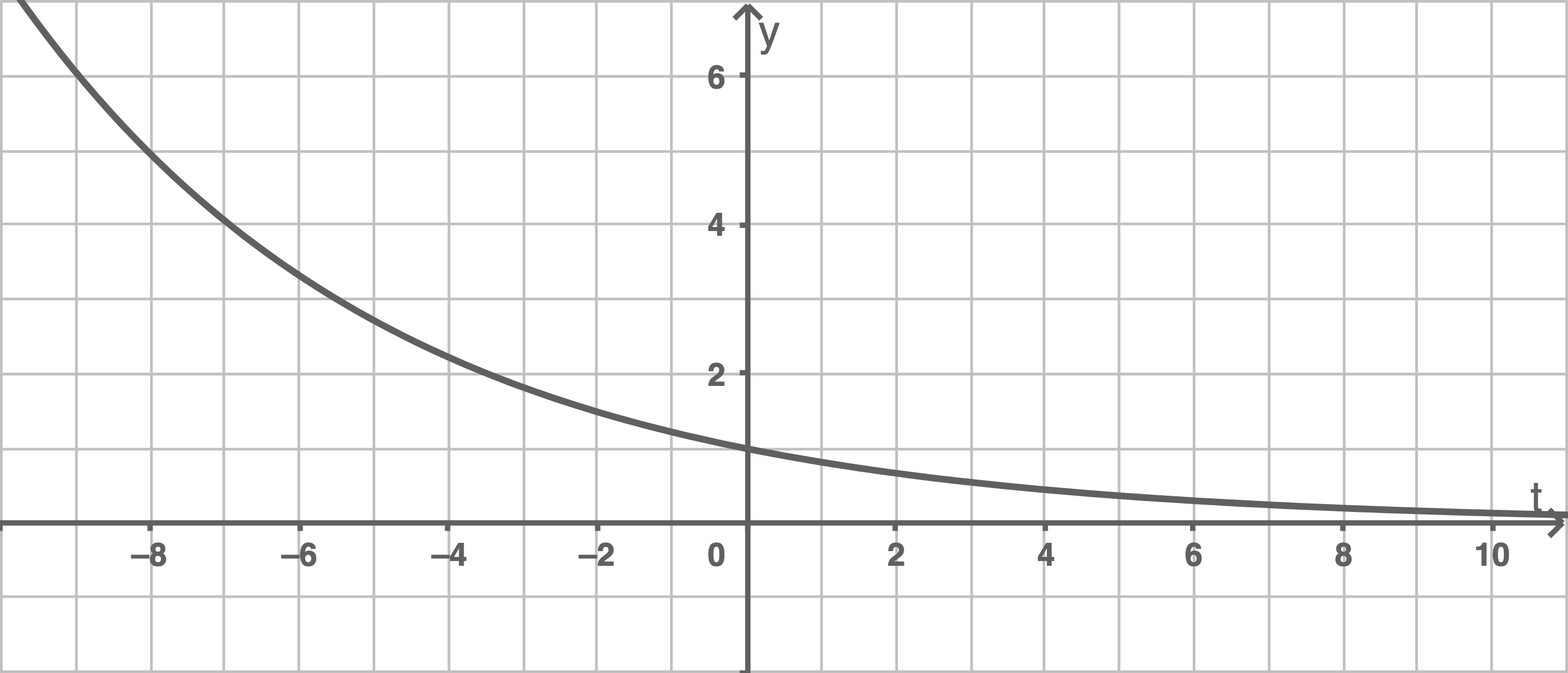

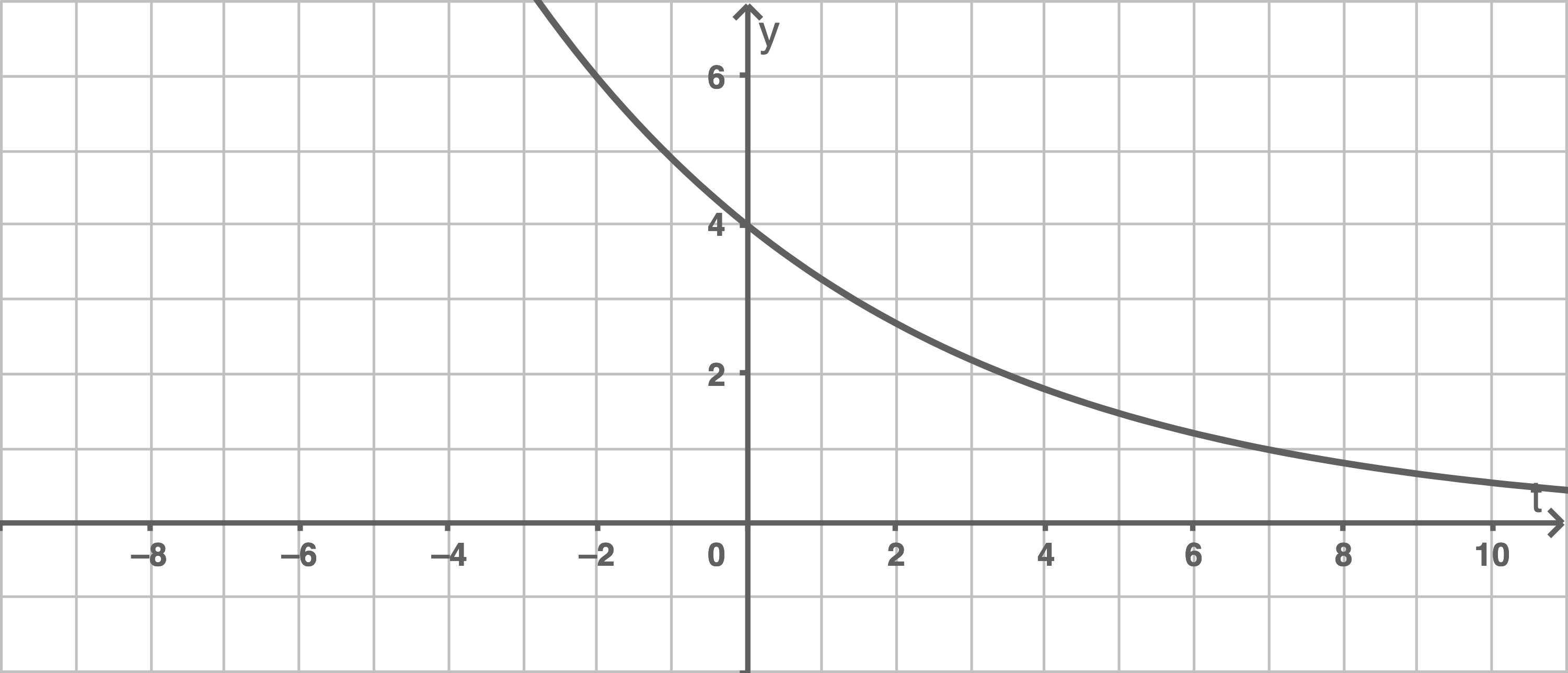

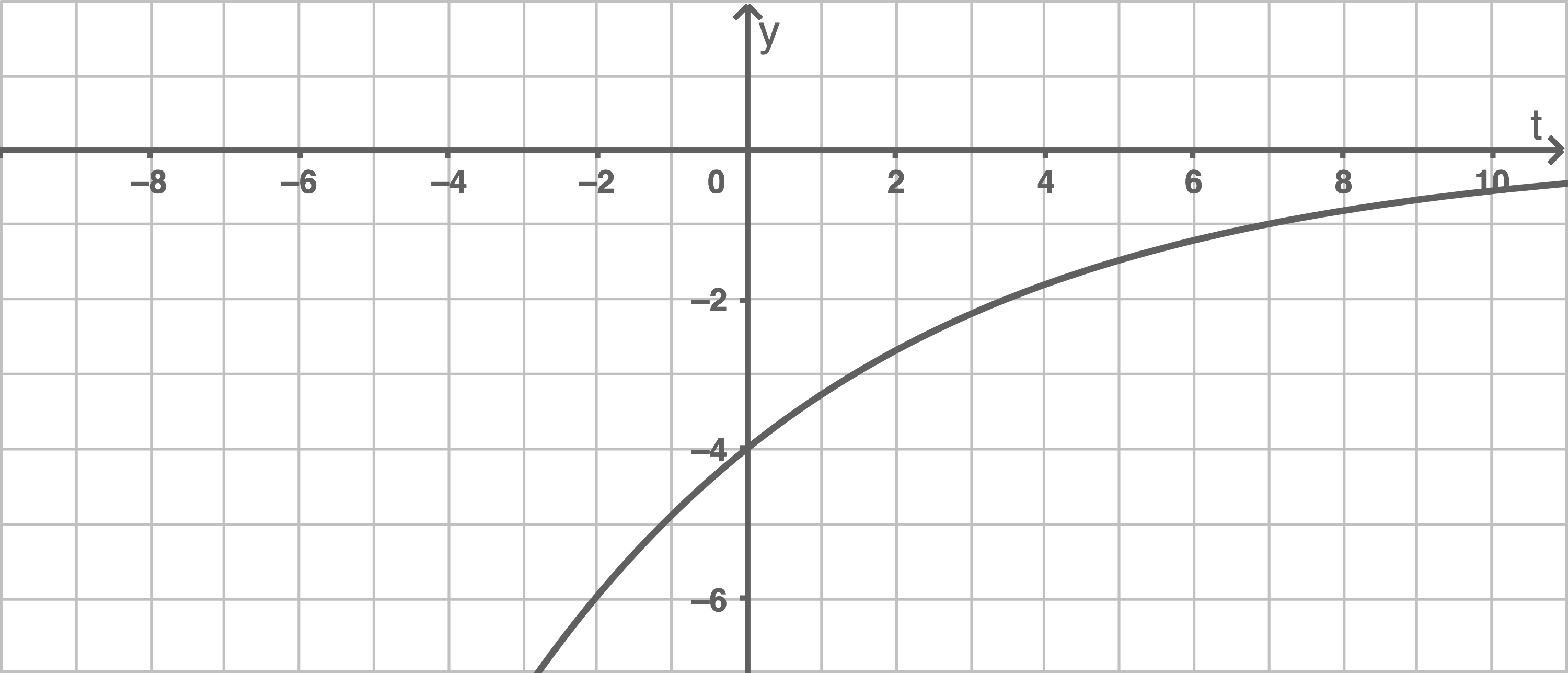
 Gib die Funktionsgleichungen von
Gib die Funktionsgleichungen von  ,
,  und
und  zu den zugehörigen Graphen an.
zu den zugehörigen Graphen an.




(6 BE)
4.1
Berechne den Flächeninhalt der Fläche, die zwischen dem Graphen von  und der
und der  -Achse im Intervall
-Achse im Intervall ![\( [0;7]\)](https://mathjax.schullv.de/a7d7b50ded416cb2a9e8a7d0e10e708ecbb9d7b8b5e0c0d8a3817cd48ba4ca08?color=5a5a5a) liegt.
liegt.
 Zur Kontrolle:
Zur Kontrolle: ![\( A\approx 26,93 \, [\text{FE}]\)](https://mathjax.schullv.de/5fab51c84931ef46f0a040c57db9effa230a0209eabae4dcca7677b8f601568b?color=5a5a5a)
![\(\big]\)](https://mathjax.schullv.de/0c6dff9ed6a80b0cc013679b53aff551dd11abb4691ba32076d10b15d6195a5d?color=5a5a5a)
(5 BE)
4.2
Zeichne die Fläche aus Aufgabe 4.1 in das nebenstehende Koordinatensystem sowie die Fläche, die zwischen der Geraden  und dem Graphen der Funktion
und dem Graphen der Funktion  im Intervall
im Intervall ![\( [0;7]\)](https://mathjax.schullv.de/a7d7b50ded416cb2a9e8a7d0e10e708ecbb9d7b8b5e0c0d8a3817cd48ba4ca08?color=5a5a5a) liegt, in das Koordinatensystem (3) aus Aufgabe 3.
Beide Flächen haben denselben Flächeninhalt.
Bestimme den Integralwert
liegt, in das Koordinatensystem (3) aus Aufgabe 3.
Beide Flächen haben denselben Flächeninhalt.
Bestimme den Integralwert
 mit Hilfe dieser Flächen unter Verwendung des Ergebnisses aus Aufgabe 4.1.
mit Hilfe dieser Flächen unter Verwendung des Ergebnisses aus Aufgabe 4.1.

(6 BE)
4.3
Berechne den Wert
 und deute diesen im Sachzusammenhang.
und deute diesen im Sachzusammenhang.
(5 BE)
1.1
Da  eine Gerade ist, kann der
eine Gerade ist, kann der  -Achsenabschnitt 2 und die Steigung
-Achsenabschnitt 2 und die Steigung  direkt abgelesen werden. Es folgt somit, dass
direkt abgelesen werden. Es folgt somit, dass  durch die Punkte
durch die Punkte  und
und  verläuft.
verläuft.
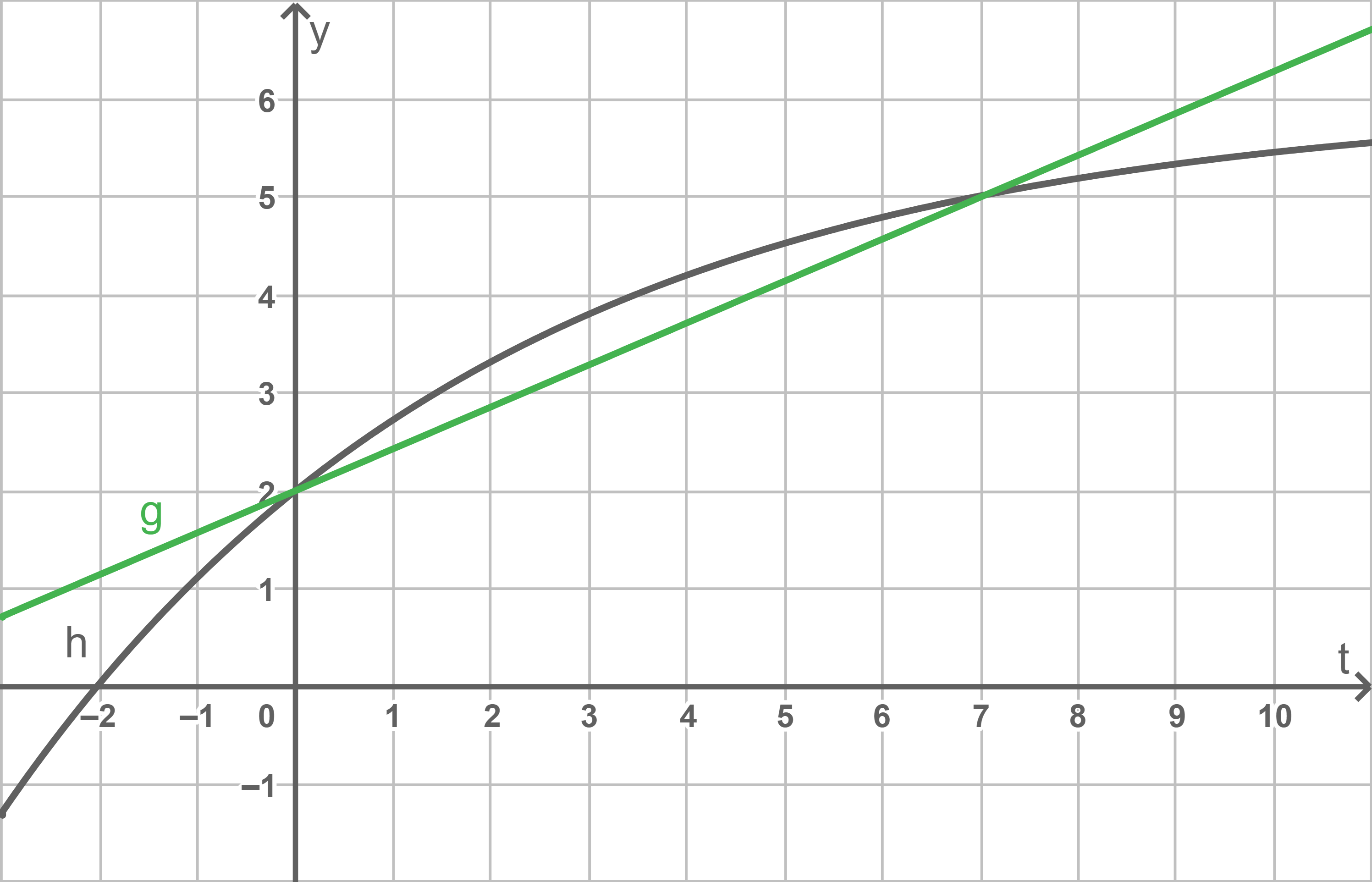

1.2
Der Graph von  steigt konstant, der Graph von
steigt konstant, der Graph von  hingegen ist nicht konstant, seine Steigung nimmt kontinuierlich ab.
Wenn das Wachstum des Baumes mit der Funktion
hingegen ist nicht konstant, seine Steigung nimmt kontinuierlich ab.
Wenn das Wachstum des Baumes mit der Funktion  modelliert werden würde, würde der Baum immer weiter mit der selben Geschwindigkeit wachsen. Das ist in der Realität nicht möglich.
Bei der Funktion
modelliert werden würde, würde der Baum immer weiter mit der selben Geschwindigkeit wachsen. Das ist in der Realität nicht möglich.
Bei der Funktion  nimmt die Wachstumsgeschwindigkeit immer weiter ab, der Baum wächst also im Laufe der Zeit immer langsamer. Daher ist die Funktion
nimmt die Wachstumsgeschwindigkeit immer weiter ab, der Baum wächst also im Laufe der Zeit immer langsamer. Daher ist die Funktion  auf lange Sicht besser für eine realistische Modellierung des Baumwachstums geeignet.
auf lange Sicht besser für eine realistische Modellierung des Baumwachstums geeignet.
2.1
Es gilt  und somit auch
und somit auch  Für
Für  gilt folglich:
gilt folglich:
![\(\begin{array}[t]{rll}
\lim\limits_{t\to\infty}\left(6-4 \cdot \mathrm e^{-0,2\cdot t}\right)&=& 6-0& \\[5pt]
&=& 6
\end{array}\)](https://mathjax.schullv.de/9277444842782733d2b78db814e800857a7559d9a2ac6732128abbe76abe57c7?color=5a5a5a) Es folgt also, dass nach langer Zeit, das heißt für große Werte von
Es folgt also, dass nach langer Zeit, das heißt für große Werte von 
 gegen 6 strebt.
Da sich die
gegen 6 strebt.
Da sich die  -Funktion für
-Funktion für  jedoch nur dem Wert Null annähert, dabei aber stets größer als Null ist und den Wert von Null nie erreicht bzw. unterschreitet, wird der exakte Wert
jedoch nur dem Wert Null annähert, dabei aber stets größer als Null ist und den Wert von Null nie erreicht bzw. unterschreitet, wird der exakte Wert  ebenso nie erreicht bzw. überschritten.
ebenso nie erreicht bzw. überschritten.
2.2
Es soll gelten:
Nach ca. 9,5 Jahren hat die Höhe des Baumes somit  des Wertes aus Aufgabe 2.1 erreicht.
des Wertes aus Aufgabe 2.1 erreicht.
2.3
Gleichung der Ableitungsfunktion angeben
Mit der Kettenregel folgt für die Ableitung  von
von  Wert angeben
Wert angeben
![\( \begin{array}[t]{rll}
h‘(4)&=& 0,8\cdot \mathrm e^{-0,2\cdot 4} \\[5pt]
&=& 0,8\cdot \mathrm e^{-0,8}\\[5pt]
&\approx& 0,36
\end{array}\)](https://mathjax.schullv.de/4a20ea70a3ed5ae3d772e0b4066ae6a1bdf7e9b86f02f103056bb7450284a14f?color=5a5a5a) Wert deuten
Da die Funktion
Wert deuten
Da die Funktion  die Höhe des Kirschbaumes modelliert, gibt
die Höhe des Kirschbaumes modelliert, gibt  folglich die Wachstumsgeschwindigkeit des Kirschbaums in Metern pro Jahr an.
4 Jahre nach dem Einpflanzen beträgt die momentane Wachstumsgeschwindigkeit des Baumes also ca.
folglich die Wachstumsgeschwindigkeit des Kirschbaums in Metern pro Jahr an.
4 Jahre nach dem Einpflanzen beträgt die momentane Wachstumsgeschwindigkeit des Baumes also ca. 
3
Funktionsgleichung von  bestimmen
Ein Vegleich von
bestimmen
Ein Vegleich von  und
und  liefert, dass der Graph von
liefert, dass der Graph von  im Vergleich zum Graphen von
im Vergleich zum Graphen von  an der
an der  -Achse gespiegelt ist.
Es folgt:
-Achse gespiegelt ist.
Es folgt:
![\(\begin{array}[t]{rll}
f_2(t)&=& f_1(-t) & \\[5pt]
&=& \mathrm e^{0,2\cdot (-t)}& \\[5pt]
&=& \mathrm e^{-0,2\cdot t}
\end{array}\)](https://mathjax.schullv.de/4dd2fd478432cc5dee7655e4db9b79f4ffcd808e4abefad9195d59bd5d6275e6?color=5a5a5a) Funktionsgleichung von
Funktionsgleichung von  bestimmen
Da der Graph von
bestimmen
Da der Graph von  im Vergleich zu dem von
im Vergleich zu dem von  schneller fällt, wurde dieser entlang der
schneller fällt, wurde dieser entlang der  -Achse gestreckt.
Durch die Streckung in
-Achse gestreckt.
Durch die Streckung in  -Richtung gilt für die Gleichung von
-Richtung gilt für die Gleichung von 
 Einsetzen der Koordinaten eines Punktes, der auf
Einsetzen der Koordinaten eines Punktes, der auf  liegt, liefert:
Die Funktionsgleichung ergibt sich also zu:
liegt, liefert:
Die Funktionsgleichung ergibt sich also zu:  Funktionsgleichung von
Funktionsgleichung von  bestimmen
Im nächsten Schritt wird der Graph von
bestimmen
Im nächsten Schritt wird der Graph von  an der
an der  -Achse gespiegelt.
Es folgt:
-Achse gespiegelt.
Es folgt:
![\(\begin{array}[t]{rll}
f_4(t)&=& -f_3(t)&\\[5pt]
&=& - 4\cdot \mathrm e^{-0,2\cdot t}&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/d05fbbb248520e9e6a31e3421439564ddd097087c74bedb7e6122a281c42542c?color=5a5a5a) Insgesamt ergeben sich somit:
Insgesamt ergeben sich somit:



4.1
Der Inhalt der Fläche zwischen dem Graphen von  und der
und der  -Achse im Intervall
-Achse im Intervall ![\([0; 7]\)](https://mathjax.schullv.de/b430d6d9e5a0d15f6f6995a913bd271dc9aea33a24d6c735ac10b236ec71d0fe?color=5a5a5a) beträgt folglich ca. 26,93 Flächeneinheiten.
beträgt folglich ca. 26,93 Flächeneinheiten.
4.2
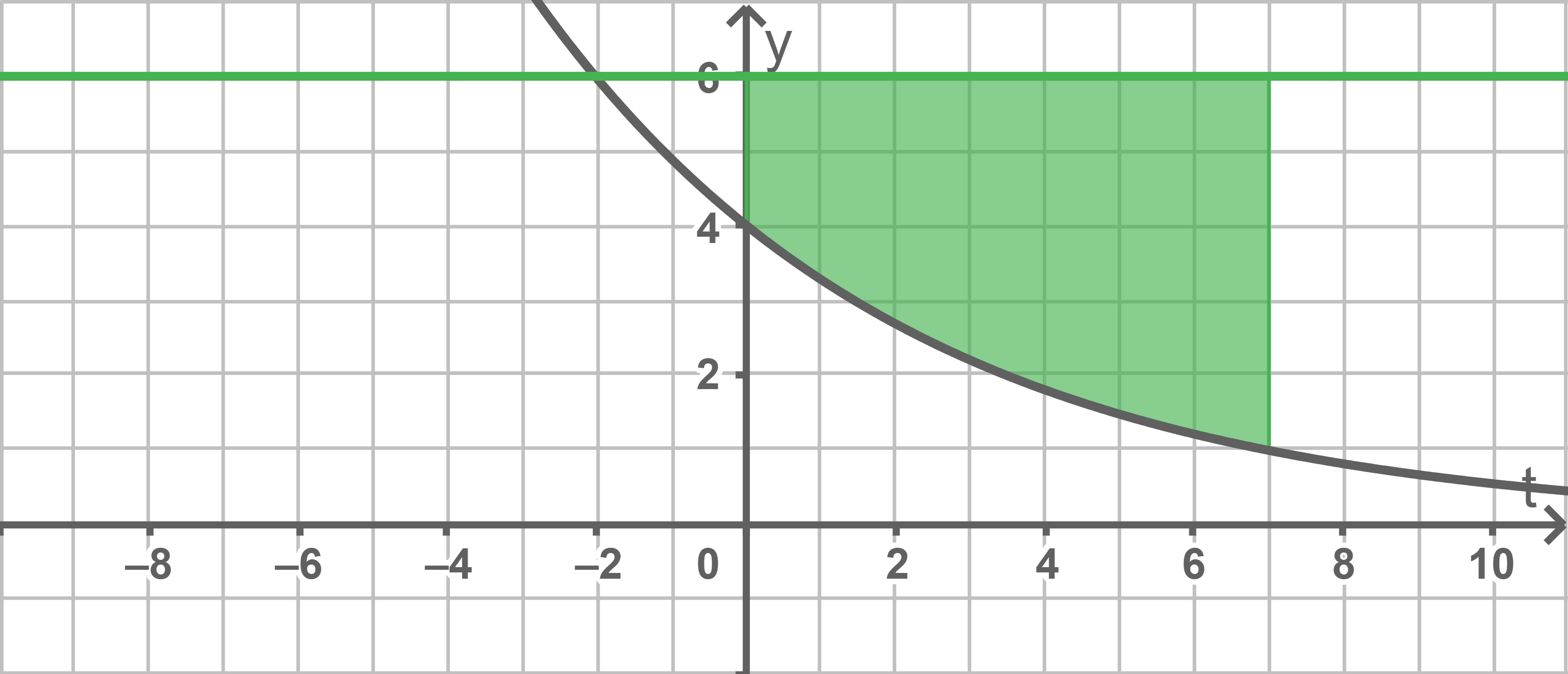
Flächen einzeichnen
Die Fläche aus Aufgabe 4.1 folgt mit:
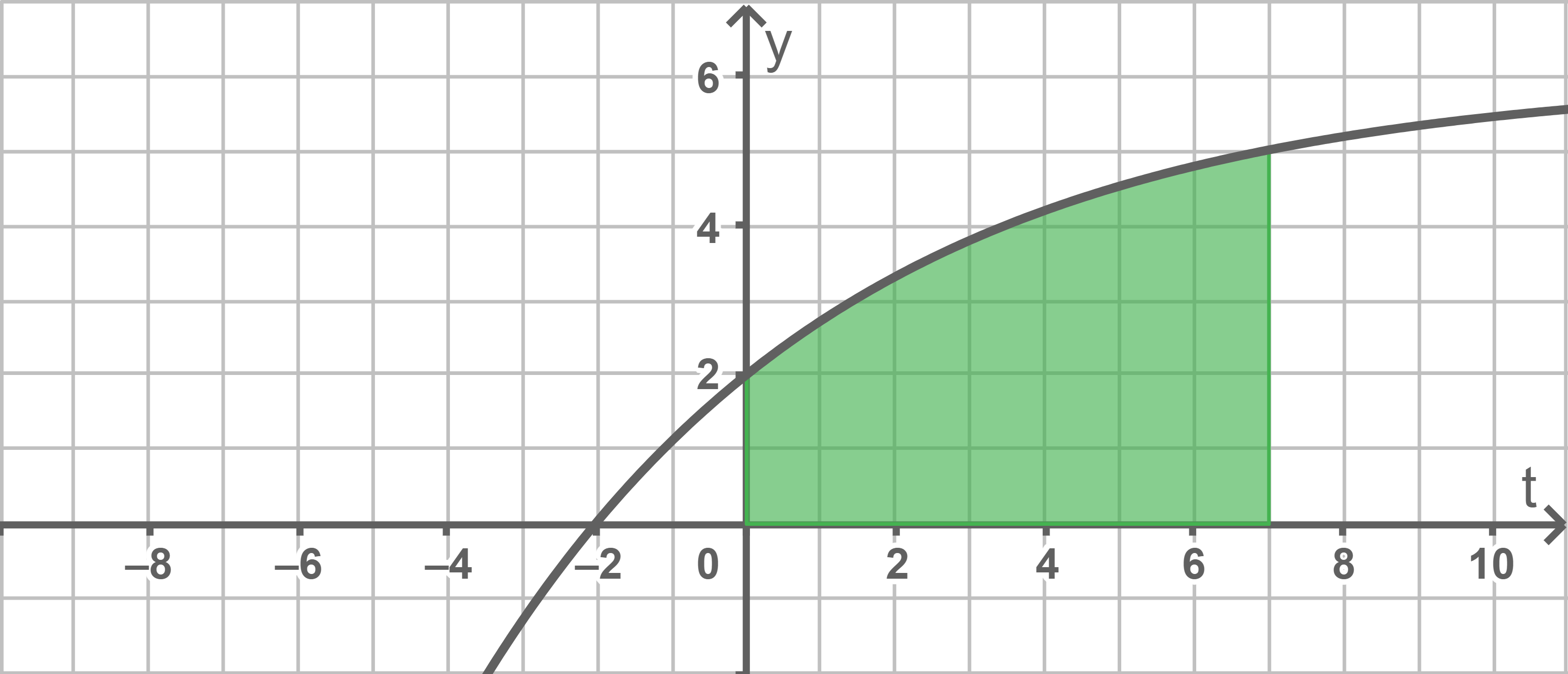 Für die Fläche zwischen der Geraden
Für die Fläche zwischen der Geraden  und dem Graphen der Funktion
und dem Graphen der Funktion  im Intervall
im Intervall ![\([0;7]\)](https://mathjax.schullv.de/e00158ca1053045578f6764e917c57aa75f21b9b8350198035116246558bee02?color=5a5a5a) ergibt sich:
ergibt sich:
 Integralwert bestimmen
Das Integral
Integralwert bestimmen
Das Integral  beschreibt die im folgenden durch Streifen markierte Fläche zwischen dem Graphen von
beschreibt die im folgenden durch Streifen markierte Fläche zwischen dem Graphen von  und der
und der  -Achse im Intervall
-Achse im Intervall ![\([0;7]:\)](https://mathjax.schullv.de/594ba68cbfce24662926a9c2756b2e66e12efa937ffba45632d4b88bb9adad7d?color=5a5a5a)
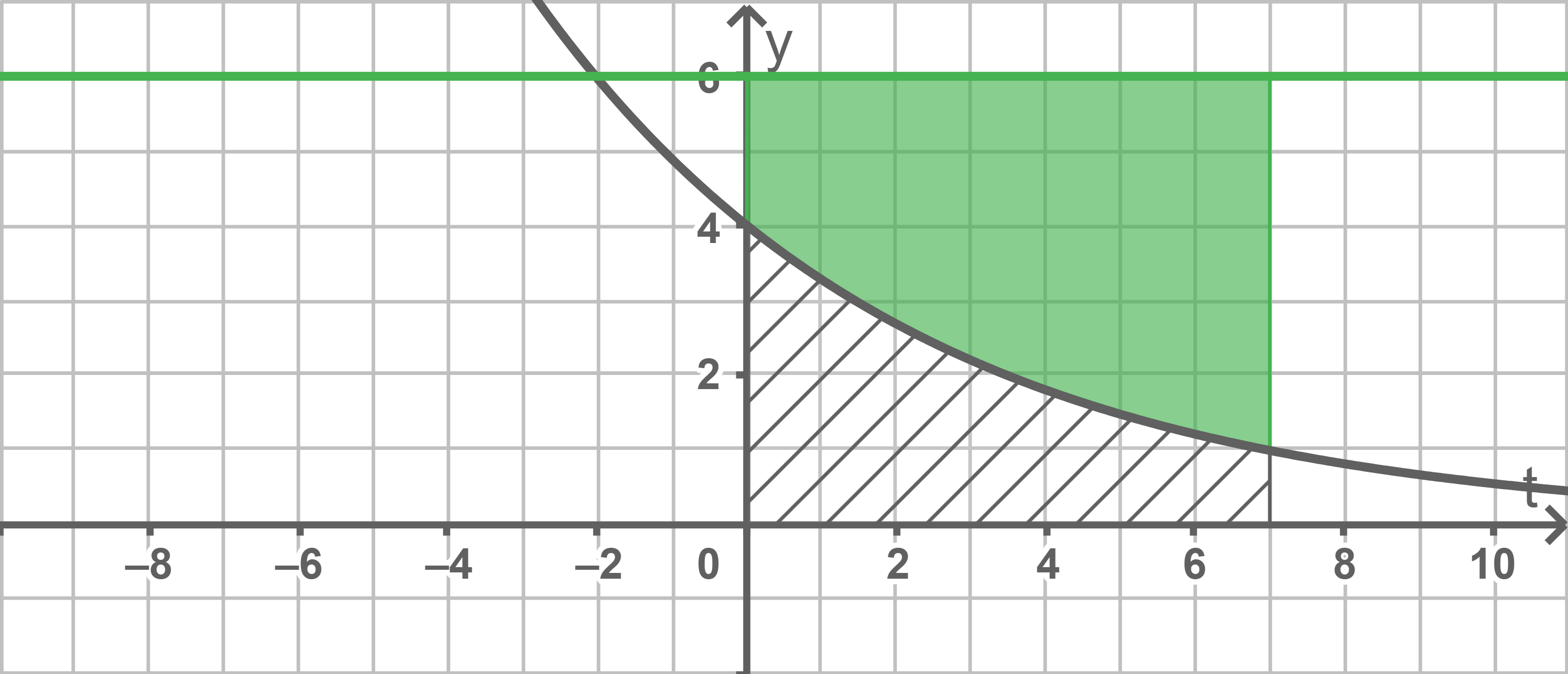 Die beiden markierten Flächen im Koordinatensystem ergeben zusammen ein Rechteck mit einer Breite von 7 Längeneinheiten und einer Höhe von 6 Längeneinheiten.
Aus der Aufgabenstellung geht hervor, dass die grün markierte Fläche den gleichen Inhalt wie die Fläche aus Aufgabe 4.1 besitzt. Diese beträgt somit ca.
Die beiden markierten Flächen im Koordinatensystem ergeben zusammen ein Rechteck mit einer Breite von 7 Längeneinheiten und einer Höhe von 6 Längeneinheiten.
Aus der Aufgabenstellung geht hervor, dass die grün markierte Fläche den gleichen Inhalt wie die Fläche aus Aufgabe 4.1 besitzt. Diese beträgt somit ca.  Es folgt also:
Es folgt also:
![\(\begin{array}[t]{rll}
\displaystyle\int_{0}^{7}f_3(t)\;\mathrm dt&=& A_{\text{Rechteck}}-A_{\text{grün}} &\\[5pt]
&=& 6\cdot 7-\displaystyle\int_{0}^{7}h(t)\;\mathrm dt &\\[5pt]
&=& 42-26,93 &\\[5pt]
&=& 15,07 \; [\text{FE}]
\end{array}\)](https://mathjax.schullv.de/a97e84079ee249c32e3b6b65d0c836b49b7c2a6933c1704b7d73cad3b6f526a5?color=5a5a5a)



4.3
Wert berechnen
Mit  als Stammfunktion von
als Stammfunktion von  folgt:
Ergebnis deuten
Der Wert
folgt:
Ergebnis deuten
Der Wert  beschreibt den mittleren Funktionswert von
beschreibt den mittleren Funktionswert von  im Intervall
im Intervall ![\([0;5].\)](https://mathjax.schullv.de/659ef5483ce5cb640d326dd5b366008ecca85ad92da628bbb9b16df35227ba5a?color=5a5a5a) Da
Da  die Höhe des Baumes beschreibt, gibt
die Höhe des Baumes beschreibt, gibt  also die durchschnittliche Wachstumsgeschwindigkeit des Baumes in den ersten fünf Jahren nach dem Einpflanzen an.
In den ersten fünf Jahren nach dem Einpflanzen wächst der Baum folglich im Schnitt
also die durchschnittliche Wachstumsgeschwindigkeit des Baumes in den ersten fünf Jahren nach dem Einpflanzen an.
In den ersten fünf Jahren nach dem Einpflanzen wächst der Baum folglich im Schnitt  pro Jahr.
pro Jahr.