B1 - Analysis

Die Tabellen in Material 1 zeigen die Entwicklung der Weltbevölkerung über einen Zeitraum von $60$ Jahren. In Material 2 sind die Wertepaare für ausgewählte Zeitpunkte als Punkte eingezeichnet.
(Weltbevölkerung in Milliarden Menschen, gerundet auf zwei Nachkommastellen, Zeit $t$ in Jahren nach Beginn des Jahres $1960$ ).

Entwicklung der Weltbevölkerung von $1960$ bis $1985$

Jahr	Weltbevölkerung (Milliarden Menschen, gerundet auf zwei Nachkommastellen)
$1960$	$3,03$
$1965$	$3,32$
$1970$	$3,68$
$1975$	$4,06$
$1980$	$4,44$
$1985$	$4,85$

Entwicklung der Weltbevölkerung von $1985$ bis $2020$

Material $1$

Jahr	Weltbevölkerung (Milliarden Menschen, gerundet auf zwei Nachkommastellen)
$1985$	$4,85$
$1990$	$5,31$
$1995$	$5,74$
$2000$	$6,13$
$2005$	$6,52$
$2010$	$6,93$
$2015$	$7,35$
$2020$	$7,78$

1.1

Zeige anhand der Tabellenwerte in Material $1$ , dass die Entwicklung der Weltbevölkerung im Zeitraum von $1960$ bis $1985$ als exponentieller Wachstumsprozess modelliert werden kann.

(4 BE)

1.2

Ein Wissenschaftler schlägt vor, die Entwicklung der Weltbevölkerung durch die Funktion $f$ mit $f(t)=3,02\cdot \mathrm e^{0,019\cdot t}$ ( $f(t)$ in Milliarden Menschen, Zeit $t$ in Jahren nach Beginn des Jahres $1960$ ) zu modellieren.
Gib die Funktionswerte in der folgenden Wertetabelle an und zeichne den Graphen der Funktion $f$ für $0\leq t\leq 60$ in das Koordinatensystem in Material 2.

$t$	$f(t)$
$0$
$10$
$20$
$30$
$40$
$50$
$60$

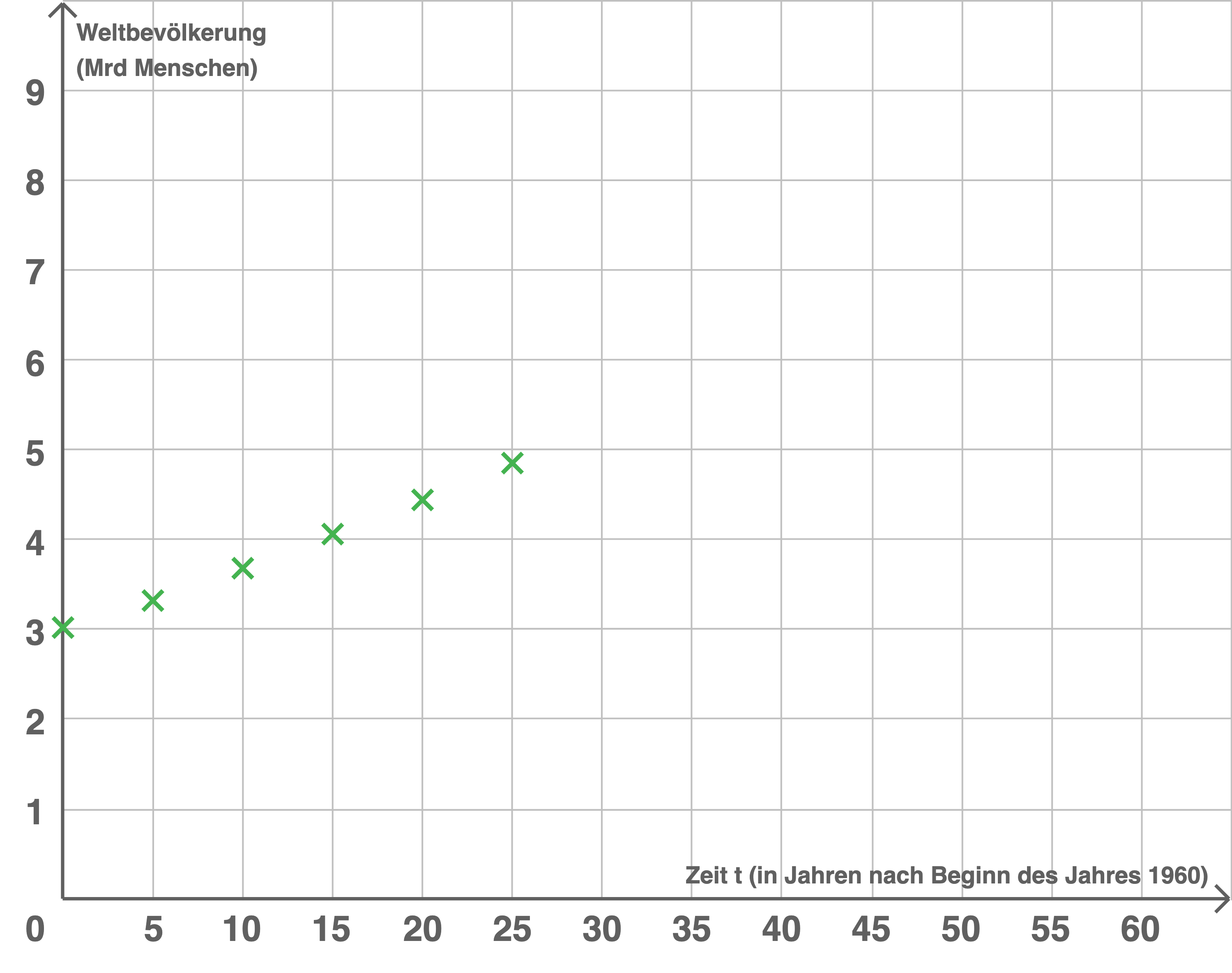Hessen GK Abi 2020 Koordinatensystem Punkte Wachstum

Material 2

Gib die Weltbevölkerung an, die der Wissenschaftler bei dieser Modellierung für den Beginn des Jahres 2020 prognostiziert.

(5 BE)

1.3

Zeichne die Wertepaare der Tabelle (Material $1$ ) für die Jahre $1990$ bis $2020$ als Punkte in das Koordinatensystem in Material $2$ . Beurteile, inwieweit der in Aufgabe 1.2 genannte Modellierungsvorschlag geeignet ist, die tatsächliche Bevölkerungsentwicklung in der Zeit vor und nach 1990 zu beschreiben.

(5 BE)

1.4

Berechne den Wert des Terms $\displaystyle \frac{1}{20}\cdot\int_{5}^{25}3,02\cdot \mathrm e^{0,019\cdot t}dt$ und deute das Ergebnis im Sachzusammenhang.

(6 BE)

Für die Zeit ab $1985$ wird eine neue Modellierung für die Entwicklung der Weltbevölkerung vorgeschlagen. Dabei wird davon ausgegangen, dass sich die momentane Änderungssrate der Bevölkerungsentwicklung durch eine Funktion $\(g$ mit $\(g$ modellhaft beschreiben lässt.
Im Gegensatz zur Funktion $f$ aus Aufgabe 1 wird für die Funktion $\(g$ der Zeitpunkt $t=0$ auf den Beginn des Jahres $1985$ festgelegt.

2.1

Für den Beginn des Jahres $1985$ geht man von einer momentanen Änderungsrate von 0,0891 Milliarden Menschen pro Jahr aus, während für den Beginn des Jahres $2020$ nur noch eine Änderungsrate von 0,078 Milliarden Menschen pro Jahr angenommen wird. Berechne auf dieser Grundlage die Werte der Parameter $d$ und $k$ und gib die Funktionsgleichung von $\(g$ an.

(5 BE)

Im Folgenden soll die momentane Änderungsrate der Bevölkerungsentwicklung durch die Gleichung $g‘(t)=0, 0891 \cdot \mathrm e^{-0,004\cdot t}$ beschrieben werden.

2.2

Die Funktion $g$ soll die Entwicklung der Weltbevölkerung ab $1985$ modellhaft beschreiben. Berechne eine Funktionsgleichung der Funktion $g$ so, dass der Funktionswert von $g$ für den Beginn des Jahres 1985 mit dem Tabellenwert dieses Jahres übereinstimmt.
[zur Kontrolle: $g(t)=27,125-22,275\cdot \mathrm e^{-0,004\cdot t}$ ]

(5 BE)

2.3

Untersuche anhand des Funktionsterms von $g$ , wie sich die Weltbevölkerung nach diesem Modell langfristig entwickelt.

(3 BE)

2.4

Berechne den Zeitpunkt, ab dem die Weltbevölkerung nach diesem Modell um weniger als 0,08 Milliarden Menschen pro Jahr zunimmt.

(3 BE)

Untersuche anhand der Werte für die Jahre $1995$ , $2005$ und $2020$ , ob sich die Funktion $g$ zur Modellierung der Entwicklung der Weltbevölkerung für den Zeitraum von $1995$ bis $2020$ besser eignet als die Funktion $f$ .

(4 BE)

1.1

Es gilt:

$1960$ - $1965$ : $\dfrac{3,32}{3,02} \approx 1,099$
$1965$ - $1970$ : $\dfrac{3,68}{3,32} \approx 1,103$
$1970$ - $1975$ : $\dfrac{4,06}{3,68} \approx 1,108$
$1975$ - $1980$ : $\dfrac{4,44}{4,06} \approx 1,094$
$1980$ - $1985$ : $\dfrac{4,85}{4,44} \approx 1,092$

Da die $5$ Quotienten nahezu konstant sind, kann die Entwicklung der Weltbevölkerung von $1960$ - $1985$ als exponentieller Wachstumsprozess dargestellt werden.

1.2

Die Funktion lautet $f(t) = 3,02 \cdot \mathrm e^{0,019 \cdot t}$ .
Durch Einsetzen der Zahlen von $0$ bis $60$ in Zehnerschritten für $t$ folgt:

$t$	$f(t)$
$0$	$3,02$
$10$	$3,65$
$20$	$4,41$
$30$	$5,34$
$40$	$6,46$
$50$	$7,81$
$60$	$9,44$

Die Weltbevölkerung zu Beginn des Jahres 2020 ergibt sich mit Einsetzen der Jahre, welche seit Beginn des Modells vergangen sind.
Das sind $60$ Jahre, also prognostiziert diese Funktion die Weltbevölkerung im Jahr $2020$ auf $9,44$ Milliarden Menschen.

Der gezeichnete Graph ist in Lösung 1.3 enthalten.

1.3

Der Graph $f(t)$ in grün und die Punkte aus der Wertetabelle der tatsächlichen Entwicklung der Weltbevölkerung in grau.

Durch einen Vergleich der grünen Punkte mit dem Graphen von $f$ folgt, dass die Werte bis $t=30$ (entspricht dem Jahr $1990$ ) identisch sind. Ab $1995$ , liegen die Werte der Weltbevölkerungsentwicklung weit unter dem Graphen von $f(t)$ .
Mit steigendem $x$ wird dieser Abstand immer größer. Daraus lässt sich schließen, dass die Funktion $f(t)$ nur im Zeitraum $1960$ - $1990$ zur Modellierung geeignet ist.

1.4

2.1

Gegeben ist die Funktion $\(g$ . Der Zeitpunkt $t=0$ entspricht dem Jahr $1985.$

Die momentane Änderungsrate im Jahr $1985$ , also bei $t=0$ , hat den Wert $0,0891.$

Somit gilt:

$\(g$

Einsetzen von $t=0$ in $\(g$ .

$\(g$ .

Gleichsetzen der Ergebnisse:

$\(\begin{array}[t]{rll} g$

$2020$ wird die Änderungsrate mit einem Wert von $0,078$ angenommen.

$2020-1985 = 35.$

Daraus folgt: $\(g$ .

Einsetzen von $d= 0,0891$ und $t=35$ in $\(g$ ergibt:

$\(g$

$k\approx -0,004$

Vollständige Lösung anzeigen

Die Funktionsgleichung lautet mit $k\approx -0,004$ und $d= 0,0891$ :
$\(g$ .

2.2

2.3

Betrachten von $g(t)$ für $t\rightarrow \infty$ .

Da der Ausdruck $-22,275\cdot \mathrm e^{-0,004 \cdot t}$ für $t\rightarrow \infty$ gegen Null geht, strebt die gesamte Funktion $g(t) = 27,125-22,275 \cdot \mathrm e^{-0,004 \cdot t}$ für $t\rightarrow \infty$ gegen $\lim\limits_{t\to\infty} 27,125 -0 = 27,125.$

Das bedeutet, dass sich die Weltbevölkerung nach diesem Modell immer weiter dem Wert $27,125$ Milliarden Menschen annähert.

2.4

$t \approx 26,93$

Vollständige Lösung anzeigen

Ab dem Zeitpunkt $t \approx 27$ - also zu Beginn des Jahres $2012$ bzw. am Ende des Jahres $2011$ - nimmt die Weltbevölkerung um weniger als $0,08$ Milliarden Menschen pro Jahr zu, da die Funktion $\(g$ streng monoton fallend ist.

Tabelle anzeigen

$Jahr$	$1995$	$2005$	$2020$
$\text{gerundeter Funktionswert von f}$	$5,87$	$7,10$	$9,44$
$\text{gerundeter Funktionswert von g}$	$5,72$	$6,56$	$7,76$

Die Abweichungen der Funktionswerte aus den in den angegebenen Tabellen gegebenen Werten für die Weltbevölkerung sind bei der Modellierung mit der Funktion $g$ für die drei betrachteten Jahre deutlich geringer als bei der Funktion $f.$ Die Funktion $g$ eignet sich daher für den Zeitraum von Beginn des Jahres $1995$ bis zum Beginn des Jahres $2020$ besser zur Modellierung der Entwicklung der Weltbevölkerung als die Funktion $f.$