A1 - Analysis

Zum Zeitpunkt $t=0$ werden einmalig 20 mg eines Medikamentes direkt in die Blutbahn eines Patienten gespritzt. Die im Blut vorhandene Medikamentenmenge (in mg) kann näherungsweise durch die Exponentialfunktion $f$ mit $f(t)=20\cdot\mathrm e^{-0,1054\cdot t}$ beschrieben werden ( $t$ misst die Zeit in Minuten nach der Injektion).

1.1

Gib die fehlenden Werte in der folgenden Tabelle an. Zeichne anschließend anhand der ermittelten Punkte den Graphen von $f$ in ein geeignetes Koordinatensystem.

$\color{#fff}{t}$	$\color{#fff}{f(t)}$
$0$	$20$
$5$
$10$
$15$	$\approx4,12$
$20$
$25$
$30$	$\approx0,85$

(7 BE)

1.2

Berechne die Zeit, nach der sich nur noch die Hälfte der anfänglichen Medikamentenmenge im Blut des Patienten befindet.

(4 BE)

Unter der medizinischen Wirkung $w(T)$ eines Medikamentes bis zum Zeitpunkt $T$ (in Minuten) versteht man den Ausdruck $w(T)$ $=\displaystyle\int_{0}^{T}f(t)\;\mathrm dt$ , wobei die Funktion $f$ die Menge des Medikamentes im Blut in Abhängigkeit von der Zeit $t$ (in Minuten) beschreibt.

2.1

Bestimme die medizinische Wirkung des Medikamentes aus Aufgabe 1 für $T=30$ unter Angabe einer Stammfunktion.

(6 BE)

2.2

Erläutere die Zeilen $(\text{I})$ bis $(\text{III})$ im Kasten und deute das Ergebnis im Sachzusammenhang.

Kasten anzeigen

(6 BE)

Das Medikament kann auch über eine Tropfinfusion verabreicht werden. Dabei gelangt jede Minute eine gleichbleibende Menge von $c=3 \;\text{mg}$ des Medikamentes in den Blutkreislauf, wobei über die Nieren in jeder Minute $k=10\,\%$ des im Blut vorhandenen Medikamentes abgebaut werden.

Für die im Blut befindliche Menge $h$ des Medikamentes in Abhängigkeit von der Zeit $t$ in Minuten gilt allgemein (mit den obigen Bezeichnungen): $h(t)=\dfrac{c}{k}\cdot\left(1-\mathrm e^{-kt}\right)$ .

3.1

Gib die Funktionsgleichung $h(t)$ für die im Blut befindliche Medikamentenmenge bei einer Tropfinfusion an.

Begründe dann, welcher der drei Graphen (Abbildung 1) die Funktion $h$ korrekt beschreibt.

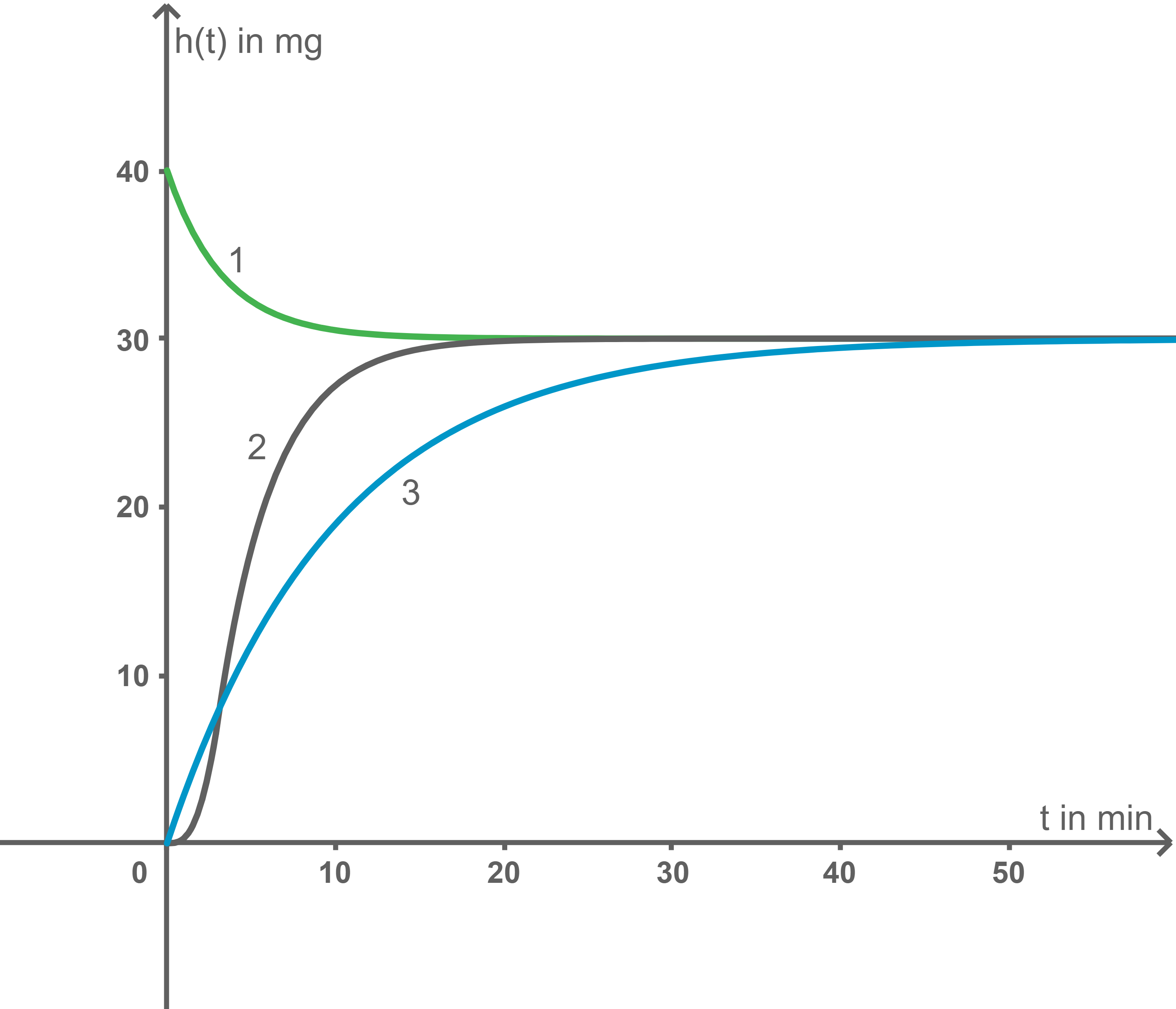
Abbildung 1

(6 BE)

3.2

Zeige, dass $H$ mit $H(t)=30\cdot\left(t+10\cdot\mathrm e^{-0,1\cdot t}\right)$ eine Stammfunktion von $h$ ist.

Berechne die medizinische Wirkung (siehe Aufgabe 2) der Tropfinfusion nach 30 Minuten.

(6 BE)

Diskutiere die Einsatzmöglichkeiten der beiden Darreichungsformen „Spritze“ und „Tropfinfusion“ anhand der betrachteten Graphen.

(5 BE)

Tabelle vervollständigen

Einsetzen der gegebenen Werte für $t$ in die Funktionsgleichung $f(t) =20 \cdot \mathrm e^{-0,1054\cdot t}$ liefert folgende Werte:

$\color{#fff}{t}$	$\color{#fff}{f(t)}$
$0$	$20$
$5$	$\approx 11,81$
$10$	$\approx 6,97$
$15$	$\approx 4,12$
$20$	$\approx 2,43$
$25$	$\approx 1,43$
$30$	$\approx 0,85$

Graph einzeichnen

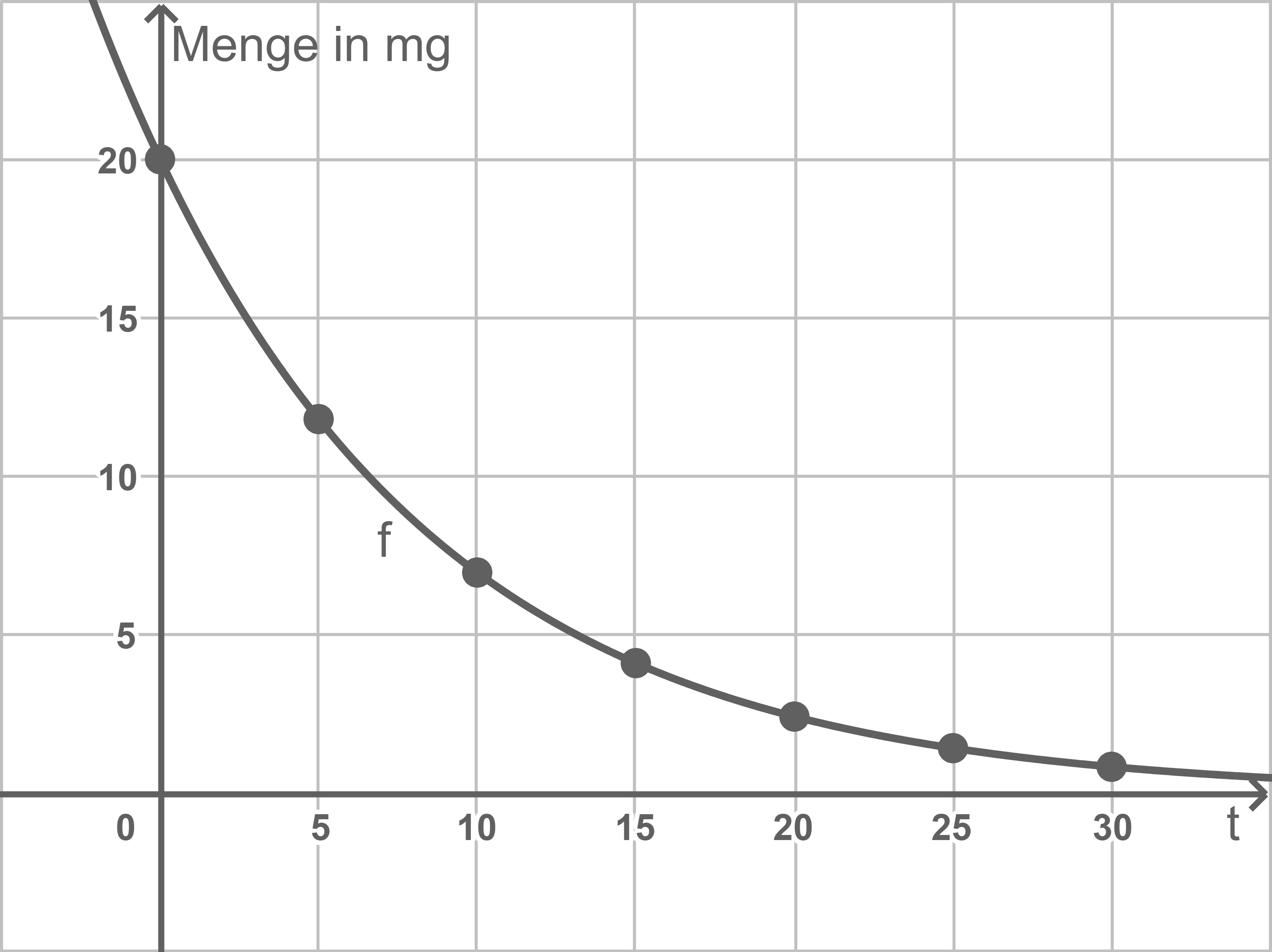
1.2

Dem Patienten wurden $20\;\text{mg}$ des Medikaments injiziert. Für den gesuchten Zeitpunkt soll also gelten:

$\begin{array}[t]{rll} f(t)&=&10 \\[5pt] 20\cdot \mathrm e^{-0,1054\cdot t}&=&10&\scriptsize \mid\; :20 \\[5pt] \mathrm e^{-0,1054\cdot t}&=& 0,5& \\[5pt] -0,1054\cdot t&=&\ln\left(0,5\right)&\scriptsize \mid\; :(-0,1054)\\[5pt] t&\approx&6,58 \\[5pt] \end{array}$

Nach ungefähr 6,58 Minuten ist somit nur noch die Hälfte der gespritzten Medikamentenmenge im Blut des Patienten.

2.1

Integrieren von $f(t)$ liefert für $F:$

$\begin{array}[t]{rll} F(t) &=& \displaystyle\int f(t)\;\mathrm dt& \\[5pt] &=& \dfrac{20}{(-0,1054)} \cdot\mathrm e^{-0,1054\cdot t} +C & \\[5pt] &\approx& -189,75 \cdot \mathrm e^{-0,1054\cdot t} +C \end{array}$

Für $T=30$ gilt also:

$w(30) \approx 181,72$

Rechenweg anzeigen

2.2

Zeilen erläutern

In Zeile $(\text{I})$ wird das Integral über $f$ von $0$ bis zur oberen Grenze $T=35$ berechnet. Das Ergebnis gibt also die Wirkung des gespritzten Medikamentes in den ersten 35 Minuten an.

In Zeile $(\text{II})$ wird der Grenzwert der Funktion $w,$ das heißt der Wirkung des Medikamentes, für $T\rightarrow \infty$ berechnet. Im Sachzusammenhang bedeutet das also, dass die gesamte medizinische Wirkung des Medikamentes bei ungefähr 189,75 liegt.

In Zeile $(\text{III})$ wird das prozentuale Verhältnis zwischen der Wirkung des Medikamentes innerhalb der ersten 35 Minuten und der gesamten Wirkung berechnet.

Ergebnis deuten

Nach 35 Minuten hat das Medikament bereits $98\;\%$ seiner Wirkung im Körper des Patienten entfaltet.

3.1

Funktionsgleichung angeben

Einsetzen der Werte $c=3\;\text{mg}$ und $k=10\;\%=0,1$ aus der Aufgabenstellung in die allgemeine Funktionsgleichung von $h$ liefert:

$\begin{array}{rll} h(t)&=&\dfrac{c}{k}\cdot (1-\mathrm e^{-kt}) \\[5pt] &=&\dfrac{3}{0,1}\cdot (1-\mathrm e^{-0,1t}) \\[5pt] &=&30\cdot (1-\mathrm e^{-0,1t}) \\[5pt] &=&-30 \cdot \mathrm e^{-0,1t}+30 \end{array}$

Zuordnung begründen

Mit Hilfe einer Wertetabelle wird nun überprüft, welcher der drei Graphen die Funktion $h$ beschreibt:

$\color{#fff}{t}$	$\color{#fff}{h(t)}$
$0$	$0$
$1$	$\approx 2,85$
$2$	$\approx 5,44$
$4$	$\approx 9,89$
$6$	$\approx 13,54$
$8$	$\approx 16,52$
$10$	$\approx 18,96$

Graph 1 kann ausgeschlossen werden, da er nicht durch den Ursprung verläuft.

Anhand der weiteren Funktionswerte, wie zum Beispiel $h(10)\approx 18,96,$ kann auch Graph 2 ausgeschlossen werden.

Somit wird die Funktion $h$ vom Graphen 3 beschrieben.

3.2

Stammfunktion nachweisen

Für die Ableitung von $H(t)$ gilt:

$\(\begin{array}{rll} H$

Da die erste Ableitung von $H$ der gegebenen Funktion $h$ entspricht, ist $H$ folglich eine Stammfunktion von $h$ .

2. Schritt: Medizinische Wirkung berechnen

analog zu Aufgabe 2 ergibt sich folgende Rechnung:

$w(30) \approx 614,94$

Rechenweg anzeigen

Wird dem Patienten das Medikament mit einer Spritze verabreicht, steht es dem Körper gleich in hohen Konzentration zur Verfügung, wird allerdings relativ schnell wieder abgebaut. In Aufgabe 2 wurde gezeigt, dass nach 35 Minuten bereits $98\,\%$ der medizinischen Wirkung entfaltet wurden.

Es ist also sinnvoll, das Medikament per Spritze zu verabreichen, wenn dieses möglichst schnell wirken soll.

Gelangt das Medikament durch eine Tropfinfusion in das Blut des Patienten, steigt die Menge im Blut erst mit der Zeit langsam an. Nach ungefähr 30 Minuten wird eine einigermaßen konstante Konzentration der Medikamentenmenge im Blut erreicht, die über einen längeren Zeitraum beibehalten wird.

Es ist also sinnvoll, das Medikament durch eine Tropfinfusion zu verabreichen, wenn dieses möglichst lange wirken soll.