C1 - Lineare Algebra/Analytische Geometrie

In einem Park steht ein Pyramidenstumpf, der als Klettermöglichkeit dient und als Boulderblock bezeichnet wird. Auf den vier Seitenwänden sind Kletterrouten geschraubt. Das umliegende ebene Gelände (Boden) liegt im Modell in der $x$ - $y$ -Ebene. Eine Einheit im Koordinatensystem entspricht einem Meter in der Realität.

Im Modell sind die Punkte $A(4\mid 0\mid 0),$ $B(4\mid 4\mid 0),$ $C (0\mid 4\mid 0)$ und $D(0\mid 0\mid 0)$ die Eckpunkte der quadratischen Bodenfläche des Pyramidenstumpfs. Die Punkte $E(5\mid 0\mid 3),$ $F(5\mid 5\mid 3),$ $G (0\mid 5\mid 3)$ und $H(0 \mid 0\mid 3)$ sind die Eckpunkte der parallel zur Bodenfläche verlaufenden, ebenfalls quadratischen Fläche (Material).

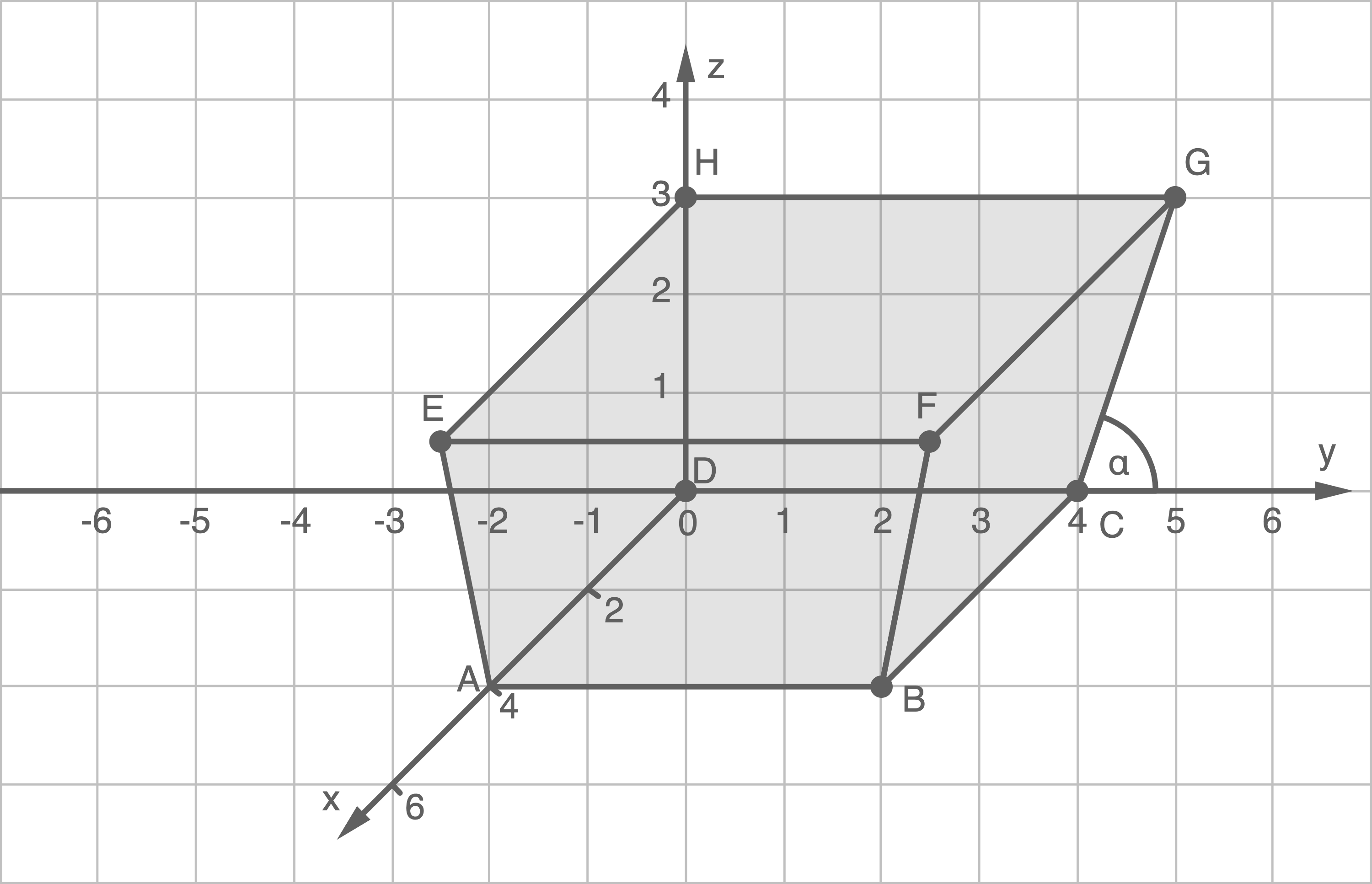
hessen mathe abi gk wtr 2022 teil c1 abbildung 1

Material

1.1

Die Seitenwand $BCGF$ liegt in der Ebene $W$ . Gib eine Parametergleichung dieser Ebene an und bestimme eine zugehörige Koordinatengleichung.
[zur Kontrolle: Eine mögliche Koordinatengleichung lautet $W: 3y-z=12$ ]

(6 BE)

1.2

Berechne den Neigungswinkel $\alpha$ der Seitenwand $BCGF$ gegenüber dem Boden (Material).

(3 BE)

1.3

Die Seitenwand $BCGF$ ist ein Trapez und soll einen neuen Farbanstrich bekommen.
Zeige, dass die Seitenwand $BCGF$ im Punkt $C$ einen rechten Winkel besitzt, und berechne auf ganze Liter gerundet, wie viel Liter Farbe benötigt werden, wenn ein Liter Farbe für $8 \,\text {m}^2$ ausreicht.

(5 BE)

1.4

Im Punkt $F$ ist ein Seil befestigt, das senkrecht nach unten hängt und den Boden berührt.
Ermittle, um wie viel Prozent die Kante $\overline{ BF }$ länger ist als das Seil.

(4 BE)

1.5

Begründe ohne Rechnung, dass die Spitze $S$ der zu dem Stumpf $ABCDEFGH$ gehörenden Pyramide auf der negativen $z$ -Achse liegt, also die Koordinaten $S(0\mid 0\mid -k )$ besitzt, und bestimme $k$ .

(5 BE)

1.6

Das Volumen des Pyramidenstumpfs in Abhängigkeit vom Parameter $k$ lässt sich mithilfe des folgenden Ansatzes ermitteln:

$\dfrac{1}{3} \cdot 5^2 \cdot(3+ k )-\dfrac{1}{3} \cdot 4^2 \cdot k$

Erläutere diesen Ansatz.

(4 BE)

1.7

Gegeben sind die Gleichungen zweier Ebenen:

$\,\text (1)$ $\overrightarrow{ x }=\left(\begin{array}{l}5 \\ 0 \\ 3\end{array}\right)+ t \cdot\left(\begin{array}{c}-5 \\ 0 \\ 0\end{array}\right)+ u \cdot\left(\begin{array}{c}-1 \\ 0 \\ -3\end{array}\right);$ $t , u \in R$

$\,\text (2)$ $x-y=0$

Eine dieser Ebenen ist die Symmetrieebene des Pyramidenstumpfs, die andere Ebene enthält eine der Seitenwände.
Gib an, welche der beiden Ebenen die Symmetrieebene ist, und beschreibe ihre besondere Lage im Koordinatensystem.
Gib die Seitenwand an, die in der anderen Ebene enthalten ist.

(5 BE)

Im Punkt $K(4\mid -4\mid 2)$ befindet sich der höchste Punkt des Kopfes eines Kletterers, der neben dem Boulderblock steht. Die Sonne scheint zu einem bestimmten Zeitpunkt in Richtung des Vektors

$\overrightarrow{ v }=\left(\begin{array}{c} -1 \\ 2 \\ -0,5 \end{array}\right).$

2.1

Berechne die Koordinaten des Schattenpunktes $\(K$ , der vom Punkt $K$ auf die Seitenwand $DAEH$ geworfen wird.

(4 BE)

2.2

Die Füße eines anderen, $1,80 \,\text{m}$ großen Kletterers befinden sich im Punkt $N(3\mid 4,5\mid 0)$ .
Untersuche, ob er dort aufrecht stehen kann.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Parametergleichung aufstellen

$W: \overrightarrow{x}=\overrightarrow{OB}+s\cdot \overrightarrow{BC} +t\cdot \overrightarrow{BG}$

Parametergleichung anzeigen

Koordinatenform bestimmen

Normalenvektor berechnen:

Rechenweg anzeigen

$\overrightarrow{n_W}= 4\cdot \pmatrix{0\\3\\-1}$

Koordinaten des Punktes $B$ einsetzen:

$\begin{array}[t]{rll} W: 0\cdot x+3\cdot y-1\cdot z&=& c &\\[5pt] 3\cdot 4-1\cdot 0&=& c &\\[5pt] 12 &=&c \end{array}$

Somit ergibt sich folgende Koordinatengleichung für die Ebene $W:$

$W: 3\cdot y-1\cdot z=12$

1.2

Ein Normalenvektor des Bodens, welcher in der $xy$ -Ebene liegt, ist $\overrightarrow{n_E} =\pmatrix{0\\0\\1}.$

Berechnen des Neigungswinkels $\alpha$ :

$\begin{array}[t]{rll} \cos (\alpha)&=&\dfrac{|\overrightarrow{n_W}\circ \overrightarrow{n_E} |}{|\overrightarrow{n_W}|\cdot |\overrightarrow{n_E} |} &\\[5pt] \cos(\alpha)&=&\dfrac{\left|\pmatrix{0\\3\\-1}\circ \pmatrix{0\\0\\1} \right|}{\left|\pmatrix{0\\3\\-1}\right|\cdot \left|\pmatrix{0\\0\\1} \right|} &\\[5pt] \cos(\alpha)&=&\dfrac{1}{\sqrt{10}\cdot 1} &\quad \scriptsize \mid\; \arccos\\[5pt] \alpha& \approx & 71,57^{\circ} \end{array}$

Der Neigungswinkel $\alpha$ der Seitenwand $BCGF$ gegenüber dem Boden beträgt folglich $71,57^{\circ} .$

1.3

Rechten Winkel nachweisen

Die Seitenwand besitzt genau dann einen rechten Winkel im Punkt $C,$ wenn die Vektoren $\overrightarrow{BC}$ und $\overrightarrow{GC}$ orthogonal zueinander sind.

Überprüfen der Orthogonalität:

Rechenweg anzeigen

$\overrightarrow{BC}\circ \overrightarrow{GC}=0$

Die Seitenwand besitzt somit im Punkt $C$ einen rechten Winkel.

Benötigte Liter an Farbe berechnen

Flächeninhalt des Trapez berechnen:

Da im Punkt $C$ ein rechter Winkel nachgewiesen wurde, beschreibt die Strecke $\overline{CG}$ die Höhe des Trapez.

Rechenweg anzeigen

$A\approx 14,23 \;[\,\text{m}^2]$

Da ein Liter Farbe für $8 \;\,\text{m}^2$ ausreicht, werden 2 Liter Farbe für die Seitenwand $BCGF$ benötigt.

1.4

1. Schritt: Länge der Kante $\overline{BF}$ berechnen

Rechenweg anzeigen

$|\overline{BF}|\approx 3,32 \;[\,\text{m}]$

2. Schritt: Länge des Seils ermitteln

Die $z$ -Koordinate des Punkts $F$ gibt den Abstand des Punkts zum Boden an.

Da das Seil senkrecht nach unten hängt, entspricht die Länge des Seils folglich der $z$ -Koordinate des Punkts $F$ und somit $3 \,\text{m}.$

3. Schritt: Prozentuale Abweichung berechnen

$p_ {\overline{BF}}=\dfrac{3,32}{3} \approx 1,11$

Die Kante $\overline{BF}$ ist somit ungefähr $11\,\%$ länger als das Seil.

1.5

Begründung

Die Spitze der Pyramide entspricht dem Punkt, in dem sich die Geraden aller Kanten des Pyramidenstumpfes schneiden.

Da die Kante $\overline{HD}$ auf der $z$ -Achse liegt, muss der Schnittpunkt mit den Geraden der restlichen Kanten ebenso auf der $z$ -Achse liegen.

Der Flächeninhalt der Fläche $EFGH$ ist größer als der Flächeninhalt der Fläche $ABCD.$ Dies kann den gegebenen Koordinaten und dem Neigungswinkel $\alpha$ entnommen werden. Somit muss die Spitze der Pyramide unterhalb des Stumpfs liegen.

Bestimmung von $k$

Zunächst wird die Gerade gebildet, die durch die Punkte $F$ und $B$ verläuft:

$s: \vec{x}= \overrightarrow{OB} + s\cdot \overrightarrow{FB}$ $= \pmatrix{4\\4\\0}+ s\cdot \pmatrix{-1\\-1 \\-3}$

Die Gerade, die durch $D$ und $H$ verläuft, hat folgende Gleichung: $r: \vec{x}= \pmatrix{0\\0\\3} + r\cdot \pmatrix{0\\0\\-3}$

Die Koordinaten von $S$ entsprechen den Koordinaten des Schnittpunktes, der Geraden. Es folgt:

Rechenweg anzeigen

$\pmatrix{4\\4\\-3}+ s\cdot \pmatrix{-1\\-1 \\-3} = r\cdot \pmatrix{0\\0\\-3}$

Aus den ersten beiden Zeilen folgt:

$\begin{array}[t]{rll} 4-s&=&0 &\quad \scriptsize \mid\;+s \\[5pt] 4&=& s \end{array}$

Aus der letzten Zeile folgt:

$\begin{array}[t]{rll} -3-3s&=& -3r \\[5pt] -3-3\cdot 4&=& -3r \\[5pt] -15&=& -3r &\quad \scriptsize \mid\;:(-3) \\[5pt] 5&=& r \end{array}$

Einsetzen in $r$ ergibt: $\overrightarrow{OS}= \pmatrix{0\\0\\3} + 5\cdot \pmatrix{0\\0\\-3}$ $= \pmatrix{0\\0\\-12}$

Folglich gilt $k=12$ und somit ergeben sich die Koordinaten von $S$ zu $S(0 \mid 0 \mid -12).$

1.6

Der Ansatz lässt sich in zwei einzelne Terme unterteilen, mit welchen jeweils das Volumen einer Pyramide berechnet wird.

Mit dem ersten Term wird das Volumen der Pyramide $ABCDEFGHS$ in Abhängigkeit vom Parameter $k$ berechnet.

Der Parameter $k$ beschreibt hierbei den Abstand vom Boden bis zur Spitze der Pyramide, $(3+k)$ entspricht folglich also der Gesamthöhe der Pyramide.

Mit dem zweiten Term wird das Volumen der Pyramide $ABCDS$ berechnet.

Durch Bildung der Differenz wird das Volumen des Pyramidenstumpfs ermittelt.

1.7

Die Ebene $(2)$ entspricht der Symmetrieebene des Stumpfs.

Sie verläuft senkrecht zum Boden und beschreibt die Diagonale des Stumpfs von den Punkten $D$ und $H$ zu den Punkten $B$ und $F.$

Ebene $(1)$ entspricht der Gleichung $E_1: \overrightarrow{x}= \overrightarrow{OE}+t\cdot \overrightarrow{EH} +u\cdot \overrightarrow{EA}$ und somit der Seitenwand $ADHE$ des Stumpfs.

2.1

1. Schritt: Gerade des Sonnenstrahls aufstellen

$\begin{array}[t]{rll} g: \overrightarrow{x}&=&\overrightarrow{OK}+s\cdot \overrightarrow{v} & \\[5pt] g:\overrightarrow{x}&=& \pmatrix{4\\-4\\2} +s\cdot \pmatrix{-1\\2\\-0,5} \end{array}$

2. Schritt: Gerade $g$ mit der Ebene $DAEH$ schneiden

Gleichung anzeigen

Aus der zweiten Zeile folgt:

$\begin{array}[t]{rll} -4+2s&=& 0 &\quad \scriptsize \mid\;+4 \quad \scriptsize \mid\;:2\\[5pt] s&=&2 \end{array}$

Durch Einsetzen von $s$ in die dritte Zeile ergibt sich $u:$

$\begin{array}[t]{rll} 2-2\cdot 0,5&=& 3-3u&\quad \scriptsize \mid\; +3u \quad \scriptsize \mid\;-1 \\[5pt] 3u&=& 3-1&\quad \scriptsize \mid\; :3 \\[5pt] u&=&\dfrac{2}{3} \end{array}$

Einsetzen von $u$ und $s$ in die erste Zeile:

$\begin{array}[t]{rll} 4-2&=& 5-5t-\dfrac{2}{3} &\quad \scriptsize \mid\; -5 \quad \scriptsize \mid\; +\dfrac{2}{3} \\[5pt] -3+\dfrac{2}{3}&=& 5t & \quad \scriptsize \mid\; :5 \\[5pt] -0,46&\approx & t \end{array}$

Für die berechneten Werte von $s$ , $u$ und $t$ schneidet die Gerade des Sonnenstrahls die Ebene $DAEH.$

3. Schritt: $s$ in $g$ einsetzen

Rechenweg anzeigen

$g:\overrightarrow{x}= \pmatrix{2\\0\\1}$

Die Koordinaten des Schattenpunktes folgen mit $\(K$

2.2

Es muss ein Punkt der Form $P(3\mid4,5\mid z)$ aus der Ebene $BCGF$ bestimmt werden:

$\pmatrix{3\\4,5\\z}=\pmatrix{4\\4\\0}+s\cdot \pmatrix{-4\\0\\0}+t\cdot \pmatrix{-4\\1\\3}$

Aus der zweiten Zeile folgt $4,5=4+t$ und somit $t=0,5.$

Für $z$ ergibt sich somit:

$z=0,5\cdot 3=1,5 \; [\,\text{m}]$

Der Kletterer im Punkt $N$ kann folglich nicht aufrecht stehen, da auf der Höhe von $1,5 \; [\,\text{m}]$ der Boulderblock beginnt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?